自行式载重车自适应悬架组群系统顺应性

赵静一 康绍鹏 程 斐 范亮贞

1.燕山大学河北省重型机械流体动力传输与控制重点实验室，秦皇岛，0660042.先进锻压成形技术与科学教育部重点实验室(燕山大学)，秦皇岛，066004



自行式载重车自适应悬架组群系统顺应性

赵静一1,2康绍鹏1,2程 斐1,2范亮贞1,2

1.燕山大学河北省重型机械流体动力传输与控制重点实验室，秦皇岛，0660042.先进锻压成形技术与科学教育部重点实验室(燕山大学)，秦皇岛，066004

对自行式载重车悬架组群系统进行了顺应性描述和顺应效果评价，针对目前传统的液压弹簧悬架系统，设计改进了一种自适应悬架组群系统，建立了整车和自适应悬架组群系统的非线性数学模型；在额定载荷为3200 kN的两纵列六轴线自行式载重车的基础上，以随机路面激励为输入，在空载和满载工况下建立了液压弹簧悬架系统和自适应悬架组群系统的仿真模型。仿真分析和现场试验对比结果表明，改进后的自适应悬架组群系统在空载和满载工况下顺应系数分别提高了103.8%与55.1%，系统液压缸输出力更加平缓，具有更好的顺应性，采用改进后的自适应悬架组群系统的自行式载重车在行驶过程中的抗冲击振动能力和改善车辆平顺性方面效果显著。

自行式载重车；自适应；蓄能器；悬架组群；顺应性

0 引言

自行式载重车的悬架系统由悬臂、摆臂、车轴、车轮组和液压缸组成[4]，为保证车辆在不同车速、不同负载和不同路况工况下的安全稳定性，所有悬架形成三组或四组独立的悬架组群共同承载车辆的负荷，构成三点或四点支撑形式，每组悬架组群由多个悬架组成，同组悬架组群内的液压缸并联连接，能够根据路况自动调整伸缩量，保证各轮胎接地比压相同，避免某一轮胎超载。根据自行式载重车载重量的不同，载重车的轴线数会相应增减，悬架组群含有的悬架数量也会相应改变。传统悬架系统利用液压缸预充油液的压缩性组成一个定刚度被动式的液压弹簧悬架，能够满足车辆较低车速的行驶要求，但对于空载和满载负荷相差较大、速度要求更高的工作场合，传统定刚度液压弹簧悬架系统在缓和路面冲击振动、减少颠簸、提高行驶过程中的平顺性、改善驾驶员操作舒适性等方面的作用是非常有限的。

本文在不改变自行式载重车原有悬架钢结构的基础上，针对悬架组群通过改进设计了一种新型悬架液压系统，使其可根据不同载荷实现刚度自适应，建立了自适应悬架组群系统数学模型，对改进前后两种悬架系统的顺应性进行仿真对比分析，对采用改进前后两种悬架系统的自行式载重车进行了现场试验。

1 悬架组群系统顺应性描述及顺应效果评价

1.1 顺应性描述

悬架组群系统顺应性是指系统应对突变载荷的能力，用给定液压系统在突变载荷作用下引起的单位压力相对变化所产生的广义容积相对变化来表征，是一个综合反映悬架组群液压系统柔性的动态指标，与液压系统和元件的结构特征参数直接相关，其中突变载荷是指能够使液压系统工作压力高于正常值并且导致系统安全阀开启产生溢流的载荷。根据定义，顺应性[5]可表示为

(1)

tc=Δt

悬架组群系统对于突变载荷的顺应过程是一个能量转换的过程，当突变载荷使液压系统工作压力超过基准压力后，这一压力开始做功，促使系统发生容积改变，将突变载荷产生的瞬间能量释放出去。图1为悬架组群系统顺应性原理示意图，可知顺应性C值为两部分阴影面积之比[6]。

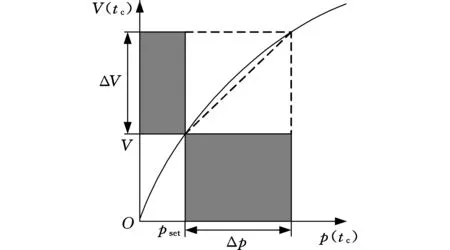
图1 顺应性原理示意图

自行式载重车载荷大、行驶速度快，受到路面激励后将产生巨大的惯性冲击振动，这些都将直接作用在车辆的悬架系统上，进而传递到车身，而悬架系统的顺应性表征为其应对惯性冲击振动的能力，是传递到平台上惯性冲击振动能量的转移或损失。无顺应的悬架系统理论上承受惯性冲击对其做的全部功，表现为悬架产生大的加速度和车体的强烈振动，平顺性差。

1.2 顺应效果评价

悬架组群系统的顺应性可用其对惯性冲击振动能量的传递特性和衰减特性来衡量，系统遇到惯性冲击振动后液压缸开始传递力，在传递过程中，由于蓄能器气体体积的改变、油液的压缩、管路变形等原因，悬架组群系统实际受到的力要远小于惯性冲击振动力。为定量评价悬架组群液压系统对特定工况路况突变载荷的顺应效果，用其对突变载荷的传递特性和衰减特性来衡量，取单位输入载荷与其对应的输出作对比。假设惯性冲击振动力为F，悬架组群系统液压缸的压力改变为pL，其有效作用面积为A，用顺应系数来表征悬架组群系统的顺应效果，其数学表达式为

(2)

同样的路面激励下，对比不同悬架系统顺应系数Cs即可反映出该系统应对冲击振动的能力，Cs越大表征系统衰减冲击振动的能力越强，顺应性越好；反之，系统较容易传递冲击，顺应性较差。悬架系统顺应性越好，车辆平顺性效果越显著。

2 自适应悬架组群系统设计及数学模型的建立

2.1 自适应悬架组群结构与工作原理

自行式载重车载质量从10 t到2000 t不等，为保证车辆在复杂工况下高速、稳定、安全行驶，由三组或四组独立的悬架组群共同承载载货平台，各组群内包含1～16个数量不等的悬架，每个悬架由钢结构、车轴、轮胎和液压控制系统组成，液压控制系统包括液压缸、液压马达和相应的控制阀组，同组悬架组群内各悬架并联连接，各液压缸并联联通。在偏载或颠簸路面工况下，可以保证组群大系统内各液压缸能自动调整伸缩量，使各轮胎接地比压相同、各悬架受力均衡，避免由于某一悬架偏载过大，出现钢结构损坏或爆胎现象等，造成严重事故。

图2为额定载荷6000 kN的两纵列十轴线自行式载重车与悬架结构示意图。当车辆为4个悬架组群支撑形式时，各组群含有5个悬架，构成四点支撑，该形式能够很好地满足载重物质量大、体积大、结构不规则和路况差等要求；当车辆为3个悬架组群支撑形式时，其中2个组群各含有5个悬架，另一个组群含有10个悬架，构成三点支撑，该形式适用于载重物结构规则、路况较好等条件，能够较容易地实现载货平台的调平动作。

由于自行式载重车在空载和满载两种工况下载荷相差较大，故在不改变其原有悬架钢结构的基础上，对悬架组群液压系统进行改进设计，设置两个蓄能器，一个是低压蓄能器，另一个是高压蓄能器，根据载重量和路况进行气体预充，将定刚度的液压弹簧悬架系统改进为具有两种非线性可变刚度的油气悬架系统[7]，可以实现车辆在不同载荷和不同路况下悬架组群系统刚度的合理变化，形成自适应悬架组群系统。改进后的自适应悬架组群系统原理如图3所示。图3中，M1n为悬架组群中液压缸的非簧载质量；m11，m12，…，m1n为悬架组群中各悬架车轴和轮胎的非簧载质量；pL为低压蓄能器气体动态压力；pH为高压蓄能器气体动态压力；z1为悬架组群车轴的位移；z10为某一悬架组群负载的位移。

在空载工况下，组群系统中只有低压蓄能器工作；在满载工况下，组群系统中低压蓄能器和高压蓄能器同时工作，两级蓄能器之间自动实现悬架组群刚度的改变，无需额外的调节。车辆在两种工况下悬架组群系统的固有频率基本保持不变，具有很好的顺应性，满足车辆减振缓冲的需求，保证车辆具有较高的平顺性。

2.2 自适应悬架组群系统设计流程

为使自行式载重车在空载和满载工况下获得良好的行驶平顺性，应在设计系统刚度时保证簧载质量振动的固有频率基本不变，车辆理想固有频率范围为1～1.5 Hz。在液压缸振动幅值范围内，要保证两级蓄能器最大工作压力不超过其最高使用压力35 MPa，最小工作压力要使液压缸能够克服约2 MPa的摩擦力。

在明确设计要求与约束条件的前提下，由自行式载重车的整体结构和升降高度的要求确定液压缸详细参数。根据车辆在空载与满载工况下的载荷，可以确定悬架处于静止平衡状态时低压蓄能器和高压蓄能器的气体压力pL1、pH1；根据选定的理想固有频率分别确定pL0vL0与pH0vH0的积，其中，pL0为低压蓄能器预充压力，vL0为低压蓄能器预充体积，pH0为高压蓄能器预充压力，vH0为高压蓄能器预充体积；再根据pL1、pH1确定两级蓄能器预充压力pL0、pH0的值，进而计算出vL0、vH0的值；最后校核车辆在两种工况下液压缸在最大行程范围内两级蓄能器的工作压力是否满足约束条件，如果不满足则调整参数pL0、pH0，直到满足约束条件为止。设计流程如图4所示。

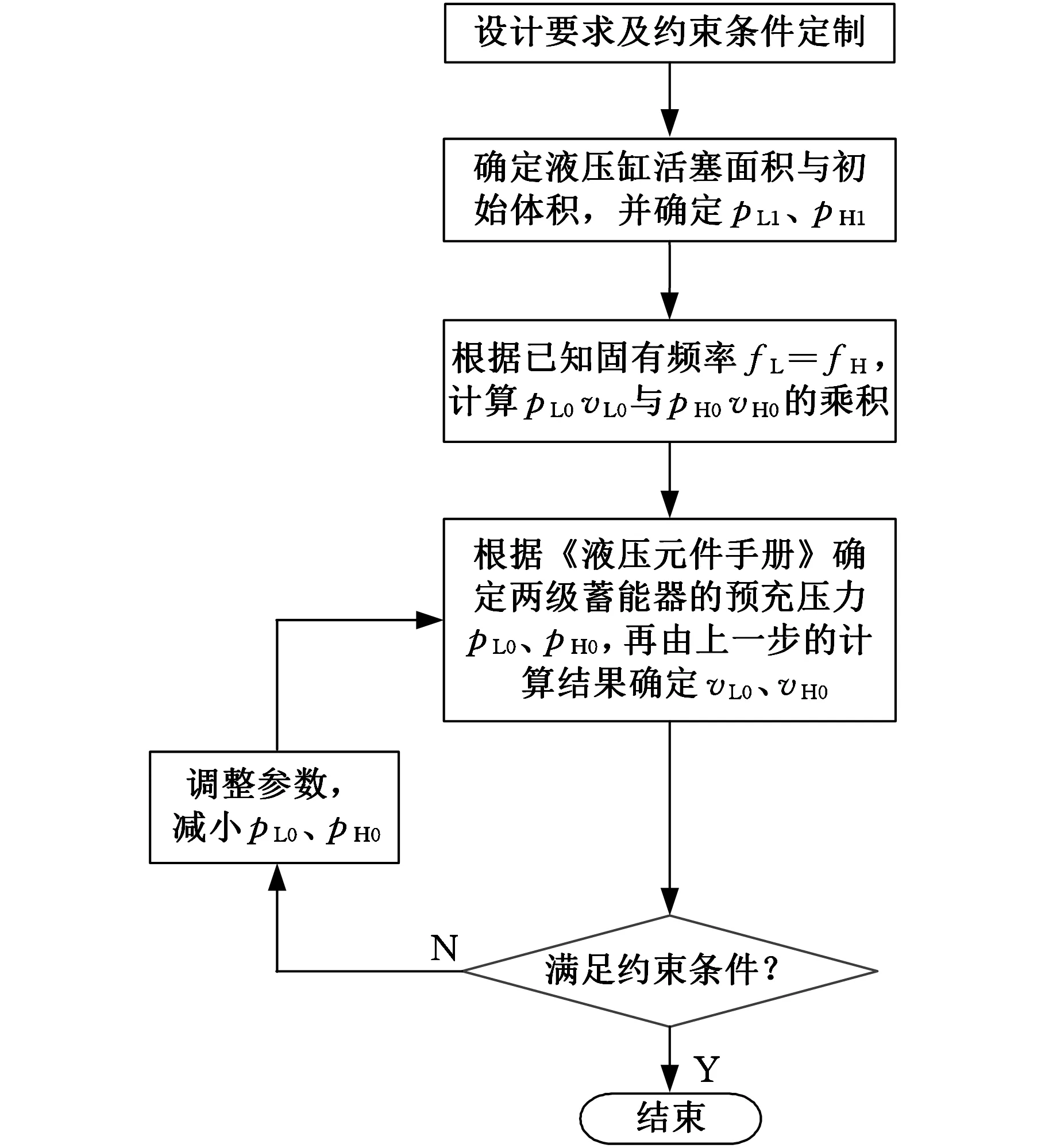
图4 自适应悬架组群系统设计流程

2.3 数学模型的建立

2.3.1 九自由度车辆振动力学模型

由四组悬架组群支撑载货平台的自行式载重车，悬架与平台之间通过带旋转副的回转支撑连接，在平台的前后分别设置了驾驶室。悬架组群和轮胎都简化为弹簧阻尼系统[8]，经过简化后的九自由度车辆振动力学模型如图5所示。

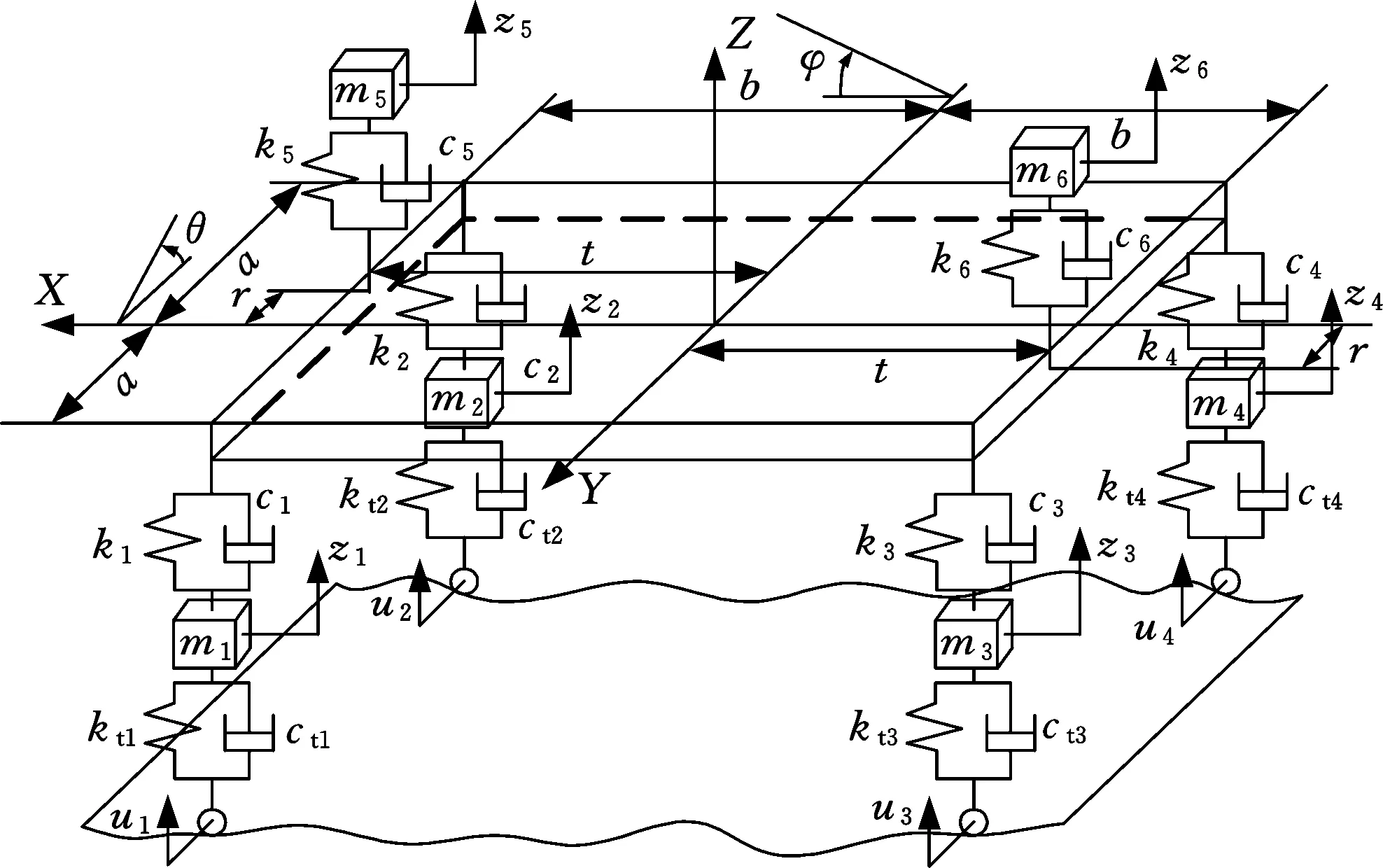
图5 九自由度车辆振动力学模型

平台具有3个自由度，分别为沿Z轴的垂向振动，沿X轴的翻转运动(旋转角为θ)，沿Y轴的颠簸运动(旋转角为φ)；z1、z2、z3、z4分别为4个悬架组群的垂直自由度，z5、z6为车辆前后驾驶室人-椅系统垂直运动的2个自由度。车辆整备质量为m，m1、m2、m3、m4分别为车辆对称布置4个悬架组群摆臂、液压缸、车轴和轮胎的质量，即悬架组群的非簧载质量，m5、m6为人-椅系统的质量，kt1、kt2、kt3、kt4为4个悬架组群的等效刚度，ct1、ct2、ct3、ct4为4个悬架组群的等效阻尼，k1、k2、k3、k4为4个悬架组群的等效刚度，c1、c2、c3、c4为4个悬架组群的等效阻尼，k5、k6为人-椅系统的等效刚度，c5、c6为人-椅系统的等效阻尼，u1、u2、u3、u4为4个悬架组群的随机路面激励。a、r分别为左右侧悬架与驾驶室距X轴的距离，b、t分别为前后侧悬架与驾驶室距Y轴的距离。可得自行式载重车在4个悬架组群和路面随机激励下的耦合振动数学微分方程：

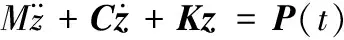
(3)

M=diag(m，Iθ，Iφ，m1，m2，…，m6)

C=[C1C2] K=[K1K2]

z=[z θ φ z1z2… z6]T

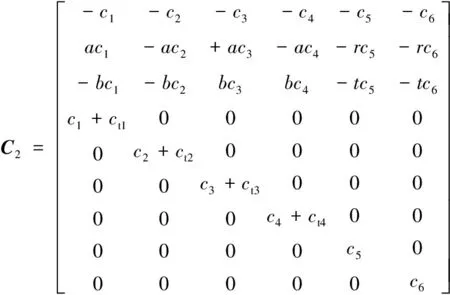
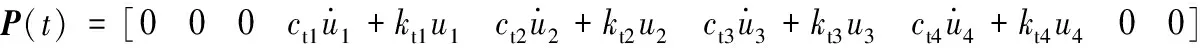
式中，Iθ为车辆绕X轴翻转运动的转动惯量；Iφ为车辆绕Y轴颠簸运动的转动惯量；P(t)为路面引起的激振力。

2.3.2 液压弹簧刚度

自行式载重车传统液压弹簧悬架的刚度是指液压缸无杆腔与液控单向阀形成完全封闭容腔内的油液在外负载的作用下，因油液压缩所形成的动态弹簧刚度。由于油液弹性模量远大于气体弹性模量，其可压缩性非常小，故在传统悬架系统中将液压弹簧刚度视为一个较小的定值[9-10]。悬架组群液压弹簧刚度可表示为

kg=NEA2/v0

(4)

式中，v0为液压缸无杆腔封闭容腔的初始体积；E为油液弹性模量；A为液压缸活塞面积；N为每个悬架组群系统并联液压缸数量。

2.3.3 两级蓄能器空载自适应刚度

在空载和满载工况平衡状态时，悬架组群液压缸无杆腔压力相差较大。空载工况下低压蓄能器主要起缓冲减振作用，高压蓄能器预充压力较大，忽略其影响。蓄能器的工作过程经过三个状态，可分为两个工作阶段：第一阶段是充液平衡过程，蓄能器压力与悬架组群液压缸负载平衡，此阶段可认为是等温过程；第二阶段是受地面激励的冲击振动过程，此过程可认为是绝热过程[11]。

空载工况下，同一悬架组群的多个悬架同时向一个方向运动时，低压蓄能器气体状态方程为

(5)

式中，vL1为静止平衡状态时低压蓄能器气体体积；vL为低压蓄能器气体动态体积；n为气体多变指数。

空载静平衡时，悬架组群系统蓄能器内气体压力为

(6)

式中，M10为空载工况下一个悬架组群簧载质量；g为重力加速度。

如图3所示，根据管道压力损失，从悬架组群某一液压缸无杆腔a处到低压蓄能器入口b处的压力关系式为

(7)

式中，pb为管道b处的压力，pb=pL；μ为油液动力黏度；lab为管路长度；d为管道内径。

联立式(5)～式(7)可求得在低压蓄能器作用下自适应悬架组群的非线性数学模型，可得液压缸的瞬时压力：

(8)

空载工况下，同一悬架组群的各轮胎向同一方向运动时，非线性自适应刚度方程为

(9)

2.3.4 两级蓄能器满载自适应刚度

满载工况状态下，同一悬架组群的多个悬架同时向一个方向运动时，两级蓄能器同时参与工作，蓄能器气体状态方程可表示为

(10)

式中，vH1为静止平衡状态时高压蓄能器体积。

满载静平衡时，悬架组群系统两级蓄能器内气体压力为

(11)

式中，M1为满载工况下一个悬架组群簧载质量。

由流体连续性方程可知，悬架组群系统两级蓄能器内气体体积为

(12)

两级蓄能器在工作过程中第二阶段的气体动态状态方程为

(13)

式中，vH为高压蓄能器气体的动态体积。

联立式(10)～式(13)可求得在两级蓄能器作用下自适应悬架组群的非线性数学模型，可得液压缸的瞬时压力：

(14)

满载工况下，同一悬架组群的各轮胎向同一方向运动时，非线性自适应刚度方程为

(15)

空载与满载工况下，由非线性自适应刚度kL、kH可求得自适应悬架组群系统振动固有频率：

(16)

式中，fL为空载工况下一个悬架组群系统振动固有频率；fH为满载工况下一个悬架组群系统振动固有频率。

2.3.5 管道阻尼

在自适应悬架组群系统中，两级蓄能器作为主要刚度元件，连接管路为阻尼元件，决定着系统的阻尼特性[12]。连接管路在压缩行程的阻尼压降见式(7)。因此，在管路中形成的阻尼力为

(17)

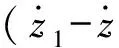
(18)

3 自适应悬架组群系统顺应性仿真分析

3.1 路面激励建模

为了更加真实地反映路面激励，采用滤波白噪声作为分析的路面输入模型。利用滤波白噪声法构建时间域的模拟路面具有物理意义清楚、计算方便的优点，可直接根据路面功率谱数值和行驶车速确定路面模型参数[13]。路面不平度微分方程为

(19)

式中，Sq(n0)为路面不平度系数，C级路面的不平度系数为256×10-6；n0为标准空间频率，n0=0.1 m-1；w(t)为均值为零的高斯白噪声；v0为车辆行驶速度；nc为路面空间下截止频率，nc=0.01 m-1。

车速为30 km/h时，据式(19)可得路面时域信号，如图6所示。

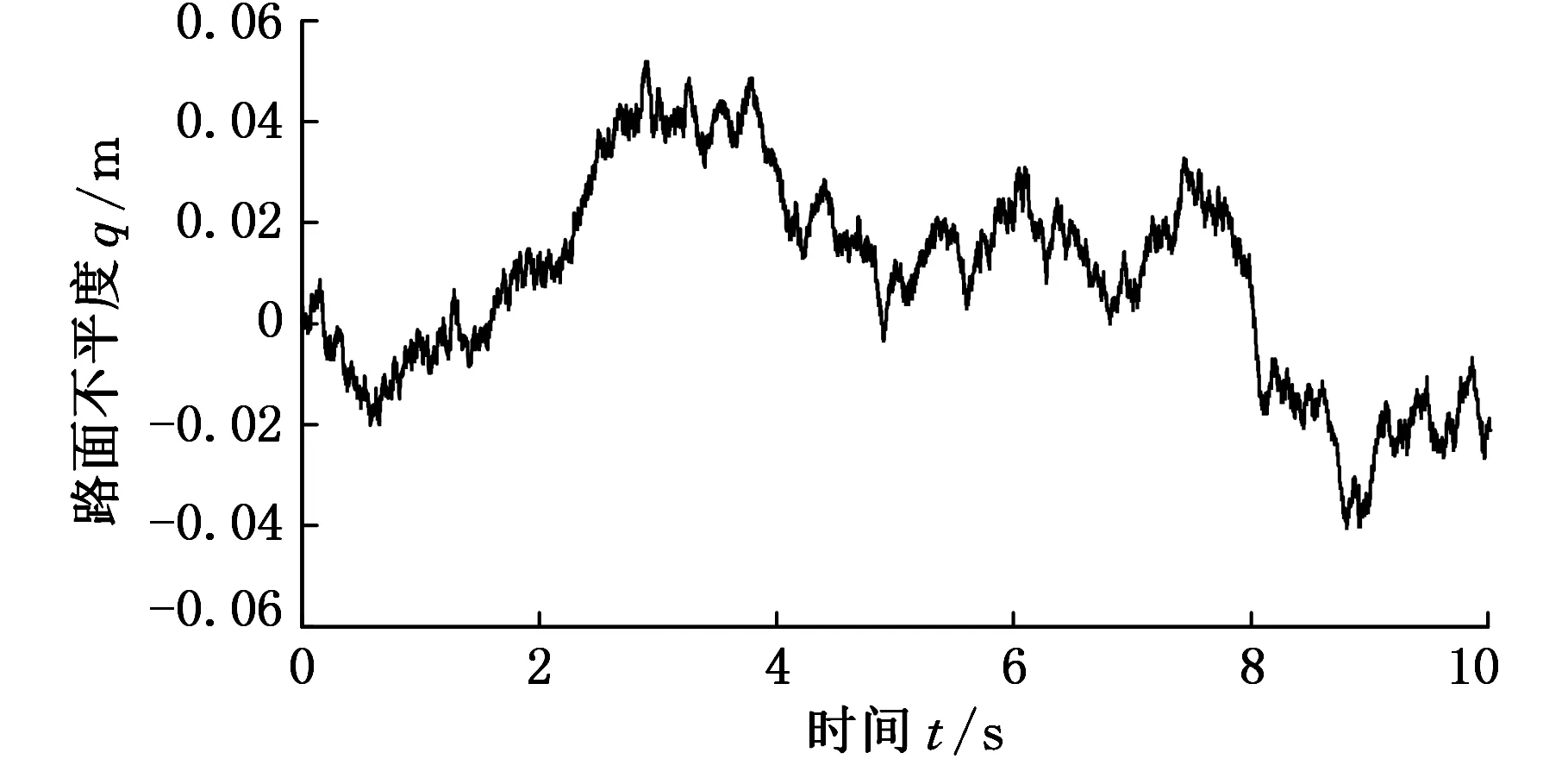
图6 路面时域信号

3.2 与传统液压弹簧悬架顺应性仿真对比

以额定载荷3200 kN的两纵列六轴线自行式载重车为例，根据建立的数学模型，在Simulink环境中建立一个含有3个悬架的自适应悬架组群系统在空载和满载工况下的振动仿真模型，对比传统液压弹簧悬架系统和改进后的自适应悬架组群系统的顺应性。将C级路面作为路面激励输入，满载工况下一个自适应悬架组群系统仿真模型如图7所示。

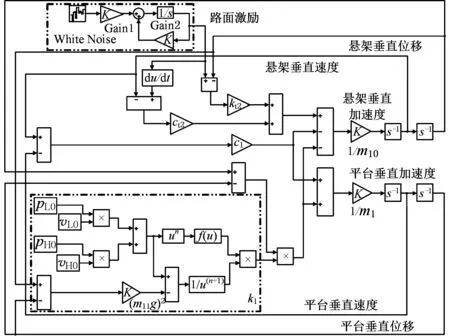
图7 自适应悬架组群系统仿真模型

在增益为0.1的阶跃信号激励下，空载工况传统液压弹簧悬架系统顺应系数为1.33×1013，自适应悬架组群系统顺应系数为2.71×1013，系统顺应性提高了103.8%；满载工况传统液压弹簧悬架系统顺应系数为1.18×1013，自适应悬架组群系统顺应系数为1.83×1013，系统顺应性提高了55.1%，说明了改进后的自适应悬架系统对于衰减和吸收来自路面的冲击振动有非常好的效果。

通过仿真对比分析在空载工况下传统液压弹簧悬架系统与自适应悬架组群系统的顺应性，如图8所示。结果表明，自行式载重车在30 km/h的车速下行驶时，改进后的自适应悬架组群系统受路面激励产生的惯性冲击经过系统的缓冲与衰减后液压缸输出力更加平缓，即平台将受到更小的振动冲击，与传统液压弹簧悬架系统相比具有更好的顺应性。同理，对比分析在满载工况下传统液压弹簧悬架系统与自适应悬架组群系统的顺应性，如图9所示。结果表明，车辆在15 km/h的车速下行驶时，改进后的自适应悬架组群系统的顺应性亦明显优于传统液压弹簧悬架系统的顺应性，车辆行驶过程中具有更好的平顺性。

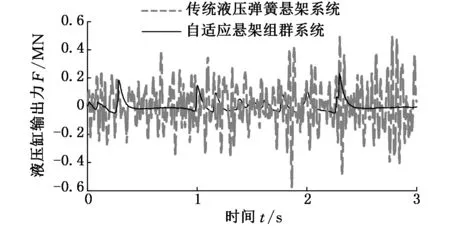
图8 空载工况两种悬架顺应性对比

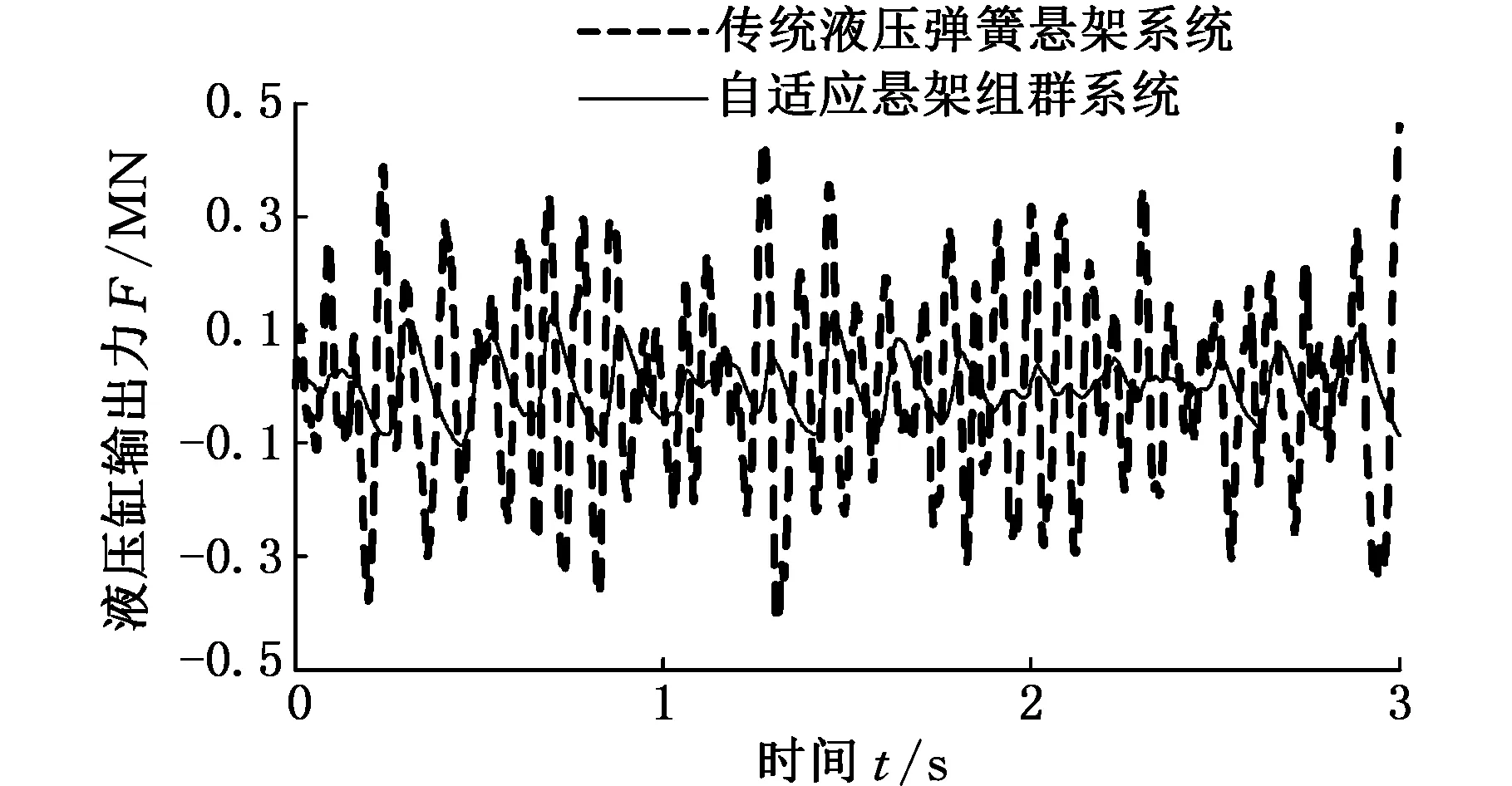
图9 满载工况下两种悬架顺应性对比

4 试验

某额定载荷为3200 kN的两纵列六轴线自行式载重车在空载和满载工况下，对比分析传统液压弹簧悬架系统和自适应悬架组群系统液压缸压力脉动情况来反映悬架系统的顺应特性，图10所示为满载试验照片。

图10 两纵列六轴线自行式载重车满载试验

如图11所示，两纵列六轴线自行式载重车在空载行驶过程中，对应采集两种悬架系统液压缸的压力信号。在同等路面、相同行驶速度下，通过对比可以明显看出自适应悬架组群系统液压缸的压力脉动得到显著改善，更加趋于平缓，与之前的仿真分析一致，同时脉动幅值也明显降低。

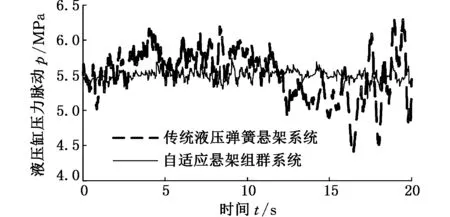
图11 空载工况下两种悬架顺应性试验对比

如图12所示，在满载行驶过程中，对应采集两种悬架系统液压缸的压力信号。在相同情况下，自适应悬架组群系统液压缸压力脉动和幅值亦得到显著改善。充分说明了改进后的自适应悬架组群系统顺应性更好，能够很好地吸收来自路面的冲击振动，进而改善车辆的行驶平顺性。

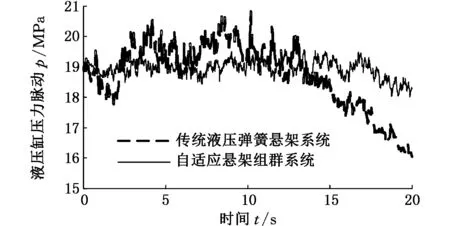
图12 满载工况下两种悬架顺应性试验对比

5 结论

(1)本文在不改变自行式载重车传统悬架钢结构的基础上设计了自适应悬架组群系统，通过对两级蓄能器参数的合理匹配，实现了悬架系统刚度的自动调节，满足了车辆在空载和满载工况下悬架簧载质量固有频率的基本一致性，建立了自适应悬架组群系统在随机路面激励下的耦合振动数学模型。

(2)在阶跃信号作用下，改进后的自适应悬架组群系统在空载和满载工况下顺应系数分别提高了103.8%与55.1%。在Simulink环境中仿真分析了一个含有三个悬架的自适应悬架组群系统在C级路面的顺应性，经过其对惯性冲击振动缓冲和衰减后，液压缸输出力更加平缓，与传统液压弹簧悬架系统相比具有更好的顺应性。

(3)对比现场两种悬架系统在行驶过程中采集液压缸压力的脉动情况，与仿真分析结果一致，充分证明了自适应悬架组群系统在提高自行式载重车行驶过程中的抗冲击振动能力、改善车辆平顺性和稳定性方面效果显著。

[1] 赵静一.大型自行式液压载重车[M].北京：化学工业出版社，2010.

[2] 李欣冉，陈无畏，陈晓新.基于刚柔耦合模型的悬架NVH性能研究[J].中国机械工程，2014，25(7)：978-983.LiXinran，ChenWuwei，ChenXiaoxin.ResearchonVehicleSuspensionNVHPerformanceBasedonFlexible-rigidCouplingModel[J].ChinaMechanicalEngineering，2014，25(7)：978-983.

[3]EslaminasabN.DevelopmentofaSemi-activeIntelligentSuspensionSystemforHeavyVehicles[D].Waterloo:UniversityofWaterloo，2008.

[4] 赵静一，程斐，郭锐，等.自行式载重车悬架升降电液同步驱动控制研究[J].中国机械工程，2014，25(7)：972-978.ZhaoJingyi，ChengFei，GuoRui,etal.ResearchonElectro-hydraulicSynchronizationDrivingControlforSelf-propelledTransporterSuspensionLifting[J].ChinaMechanicalEngineering，2014，25(7)：972-978.

[5] 侯典清，龚国芳，施虎，等.盾构推进系统突变载荷顺应特性研究[J].浙江大学学报(工学版)，2013，47(3)：522-527.HouDianqing，GongGuofang，ShiHu,etal.ComplianceCharacteristicsofPropulsionSystemofShieldTunnelingMachineunderSuddenLoad[J].JournalofZhejiangUniversity(EngineeringScience)，2013，47(3)：522-527.

[6] 施虎，杨华勇，龚国芳，等.盾构推进液压系统载荷顺应性指标和评价方法[J].浙江大学学报(工学版)，2013，47(8)：1444-1449.ShiHu，YangHuayong，GongGuofang,etal.DefinitionandEvaluationMethodforComplianceofThrustHydraulicSystemforShieldTunnelingMachine[J].JournalofZhejiangUniversity(EngineeringScience)，2013，47(8)：1444-1449.

[7] 张春辉，赵静一，田兴，等.基于模糊控制的半主动油气悬挂系统在铰接式自卸车中的应用[J].中国机械工程，2014，25(18)：2550-2555.ZhangChunhui，ZhaoJingyi，TianXing,etal.ApplicationsofSemi-activeHydro-pneumaticSuspensionSystemBasedonFuzzyControlinArticulatedDumpTruck[J].ChinaMechanicalEngineering，2014，25(18)：2550-2555.

[8]NovikovVV，SmolyanovOV.VibrationalProtectionProvidedbyAutomobileSuspensionswithBothHydraulicandInertial-frictionalShockAbsorbers[J].RussianEngineeringResearch，2009，29(1)：68-70.

[9] 叶小华，岑豫皖，赵韩，等.基于液压弹簧刚度的阀控非对称缸建模仿真[J].中国机械工程，2011，22(1)：23-27.YeXiaohua，CenYuwan，ZhaoHan,etal.ModelingandSimulationofHydraulicSpringStiffness-basedAsymmetricalCylinderControlledbyValve[J].ChinaMechanicalEngineering，2011，22(1)：23-27.

[10] 郭锐，唱荣蕾，赵静一，等.液压制动系统蓄能器充液特性研究[J].农业机械学报，2014，45(7)：7-12.GuoRui，ChangRonglei，ZhaoJingyi,etal.ResearchonAccumulatorChargingCharacteristicsofHydraulicBrakeSystem[J].TransactionsoftheChineseSocietyofAgriculturalMachinery，2014，45(7)：7-12.

[11] 赵敬凯，古正气，张沙，等.矿用自卸车油气悬架力学特性研究与优化[J].机械工程学报，2015，51(10)：112-118.ZhaoJingkai，GuZhengqi，ZhangSha,etal.ResearchandOptimizationontheMechanicalPropertyofMiningDumpTruck’sHydro-pneumaticSuspension[J].JournalofMechanicalEngineering，2015，51(10)：112-118.

[12] 杨健，苏华山，刘军辉.液压悬架系统阻尼特性分析[J].机床与液压，2015，43(11)：145-147.YangJian，SuHuashan，LiuJunhui.DampingCharacteristicsAnalysisofHydraulicSuspensionSystem[J].MachineTool&Hydraulics，2015，43(11)：145-147.

[13] 尹志新，李端芳，唐萌，等.基于MATLAB的时域路面不平度仿真研究[J].装备制造技术，2010(4)：43-44.YinZhixin，LiDuanfang，TangMeng,etal.AStudyonSimulationofPavementRoughnessBasedonMATLAB[J].EquipmentManufacturingTechnology，2010(4)：43-44.

(编辑 陈 勇)

Compliance of Self-adaption Suspension Group Systems in Selfpropelled Transporters

Zhao Jingyi1, 2Kang Shaopeng1, 2Cheng Fei1, 2Fan Liangzhen1, 2

1.Hebei Provincial Key Laboratory of Heavy Machinery Fluid Power Transmission and Control,Yanshan University,Qinhuangdao,Hebei,066004 2.Key Laboratory of Advanced Forging & Stamping Technology and Science(Yanshan University),Qinhuangdao,Hebei,066004

Through the descriptions and effect evaluations of the compliance of self-adaption suspension group systems in self-propelled transporters, a kind of self-adaption suspension group system was improved and designed in view of the present traditional hydraulic spring suspension system, and a nonlinear mathematical model of the transporter and self-adaption suspension group system was established. Based on the six axis of self-propelled transporter which was loaded 3200 kN, the simulation model of hydraulic spring suspension system and self-adaption suspension group system was built with random road surface excitation for inputs under no-load and full load conditions. Simulation analyses and field tests show that the compliance coefficient of the improved self-adaption suspension group system is increased by 103.8% and 55.1% under no-load and full-load conditions respectively, the output forces of the system hydraulic cylinder are more gentle and the compliance performance of the system is better. The ability to resist shock vibrations and the performance to ride comfort improvements have remarkable effects in the self-propelled transporter driving processes using the improved self-adaption suspension group system.

self-propelled transporter; self-adaption; energy accumulator; suspension group; compliance

2016-01-11

国家自然科学基金资助项目(51675461；11673040)

U461.4

10.3969/j.issn.1004-132X.2016.22.021

赵静一，男，1957年生。燕山大学机械工程学院教授、博士研究生导师。主要研究方向为新型液压系统开发和机电设备控制。出版专著9部，发表论文200余篇。康绍鹏，男，1986年生。燕山大学机械工程学院博士研究生。程 斐，男，1983年生。燕山大学机械工程学院博士研究生。范亮贞，男，1990年生。燕山大学机械工程学院硕士研究生。