QC新七大工具之五：矩阵图法

◆王为人

矩阵图法(Matrix Diagram)又称矩阵表法。它是利用矩阵的形式表示因素之间的相关性，从中寻求问题并探索问题解决方案的一种方法。在复杂的质量问题中存在多种影响因素，矩阵图将这些因素按照类别分别排列成矩阵的行和列，找出成对因素，在其交点考察这两个因素的相互关联程度，在此基础上再找出存在问题及其形态，从而寻求问题的解决方案。

图1为最简单的矩阵图法示意图。在图1中，A为某一个组群因素，在其之下的各具体因素为A1、A2、A3、A4、…，将它们排列成矩阵的行；B为另外一个组群因素，在其之下的各具体因素为B1、 B2、B3、B4、…，将它们排列成矩阵的列；行和列的交点表示A和B各因素之间的关系。

图1 矩阵图法示意图

矩阵图的最大优点在于可以方便地、不遗漏地寻找出对应元素之间的交点，清楚地显示对应元素的关系。它还具有以下特点：(1)因素之间的关系清晰明了，便于确定重点；(2)可用于分析成对的影响因素；(3)便于与系统图结合使用等。

矩阵图法的用途

在质量管理活动中，矩阵图法有着十分广泛的用途，特别是在理解或/和表达不同组数据之间的关系时。矩阵图法常用于解决以下问题：(1)把产品和服务的功能与顾客的体验相对应，从中找出提升顾客满意度的切入点；(2)明确应保证的产品和服务质量特性及其与各个管理机构或保证部门的关系，使质量保证体制更可靠；(3)明确实现效果与测试测量指标、方法之间的关系，建立质量评价体制或提高效率；(4)当工作流程中存在多种交织不良现象且它们之间具有若干个共同原因时，可理清这些不良现象及其产生原因的相互关系，争取从根本上消除；(5)在进行多变量分析时，研究分析从何处入手以及以什么方式收集数据等。

在执行具体工作时，矩阵图还可以用于：(1)将顾客要求与过程因素相联系时(也称关键质量矩阵)；(2)给团队成员分配任务时(也称责任矩阵)；(3)寻求、区分哪些问题影响哪些流程或服务及产品的哪个部分时；(4)探索问题的因果关系时；(5)多个任务和项目同时执行产生冲突时寻求补充解决方案等。

矩阵图的类型

矩阵图法的应用方法是将被分析对象以因素群组方式适当地表示在矩阵图上。根据因素群组的数量，可以将矩阵图按照其因素维度进行分类，依照形状命名。具体应用时可按对象的因素群组选择并灵活运用适当的矩阵图形。常见矩阵图有以下几种：

(1)L型矩阵图。把一对群组的现象以二维矩阵的行和列排列为二元表的形式表达。这是最简单的一种矩阵图，适用于若干目的与若干手段的对应关系，或若干结果和若干原因之间的关系。如图1所示。

(2)T型矩阵图。有3个因素组群，组成A、C和B、C两两之间因素组群之间的关系，可以看成两个L型矩阵的叠加(图2)。例如，在分析质量问题时，T型矩阵图可以用于“客户不满意现象/不符合现象—原因—流程”之间的关系，也可以用于分析探索药品成分新用途的 “药品成分—特性—用途”之间的关系等。

图2 T型矩阵图

(3)Y型矩阵图。有3个因素组群，是把A因素组群与B因素组群、B因素组群与C因素组群、C因素组群与A因素组群3个L型矩阵图叠加在一起而形成的组合矩阵图(图3)。Y型矩阵图也可在平面上展开，形成如图4所示的菱形矩阵图。

图3 Y型矩阵图

图4 菱形矩阵图

(4)C型矩阵图。有3个因素组群，区别于T型和Y型分析因素的两两相关性，C型矩阵图是分析A、B、C因素组群的3个因素之间的相关性。图5中，以A、B、C 3个因素组群为边做出半个六面体，以A、B、C 3个因素组群所确定的三维空间上的焦点的相关性为考察对象。

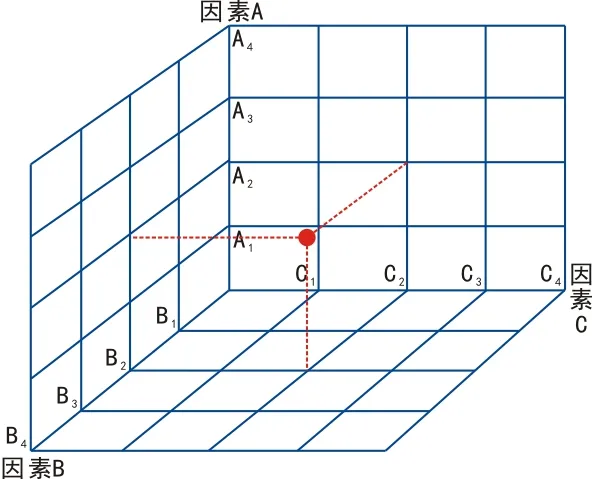
图5 C型矩阵图

(5)X型矩阵图。有4个因素组群，可以看做是将A因素组群与B因素组群、B因素组群与C因素组群、C因素组群与D因素组群、D因素组群与A因素组群4个L型矩阵图叠加而形成的组合矩阵图(图6)。这种矩阵图表示A与 C、D，B与C、D，C与A、B，D与A、B这两个两对因素组群间的相互关系。例如，“管理职能—管理项目—输入信息—输出信息”就可以用X型矩阵图进行分析。

图6 X型矩阵图

(6)五角型矩阵图。有5个因素组群，可以看做是将A因素组群与B因素组群、B因素组群与C因素组群、C因素组群与D因素组群、D因素组群与E因素组群、E因素组群与A因素组群5个L型矩阵图叠加而形成的组合矩阵图(图7)。这种矩阵图表示A与 B、E，B与A、C，C与B、D，D与C、E，E与D、A这5对因素组群间的相互关系。五角型矩阵图更为复杂，常用于多因素组群的两两之间相关性分析。

图7 五角型矩阵图

(7)单组自相关矩阵图。这是最简单的一种矩阵图，它只包含1个因素组群，是各个因素两两之间的相关性分析。图8给出了净水因素的分析示例。单组自相关矩阵图使用简单、明了，适用于因素较少或不易分组或分组没有意义等场合。

图8 净水因素单组自相关矩阵图示例

矩阵图的适用场合

矩阵图不同的形状取决于比较组数的多少。根据各因素组群之间的关系结构，各种矩阵图的使用场合可以总结如下：(1)单组自相关矩阵用于只有1组或不分组时各因素之间的比较；(2)L型矩阵用于两组间的比较；(3)T型矩阵用于3组的比较。某一因素组群与其他两因素组群分别比较，他们之间不做相互比较；(4)Y型矩阵(或菱型矩阵)用于3组的比较，且3个因素组群两两循环比较；(5)C型矩阵用于3组的比较，矩阵图表现为三维空间；(6)X型矩阵用于4组间的比较，每个因素组群与相邻的两组相比较，与对面的因素组群不建立联系；(7)五角型矩阵用于5组间的比较，每个因素组群与相邻的两组相比较，与不相邻的因素组群不建立联系。表1概括了上述各种矩阵图的适用场合。

表1各种矩阵图的适用场合

图形组数(组)说明单组自相关矩阵1A←→A,组内各因素之间的关系L型矩阵2A←→BT型矩阵3B←→A←→C,但没有建立B、C之间的联系Y型矩阵3A←→B←→C←→A菱型矩阵3Y型矩阵图的另一种表达形式C型矩阵3A、B、C 3者之间的关系X型矩阵4A←→D←→B←→C←→A,但没有建立A、B及C、D之间的联系五角型矩阵5A←→B←→C←→D←→E←→A,但没有建立A、C,A、D,B、D,B、E, C、A,C、E之间的联系

表2矩阵图的常用符号

符号说明符号说明◎强相关+正相关○中等相关0中性相关△弱相关或潜在相关-负相关空格不相关S供应商↑或↗*左边的项影响上边的项C顾客↓或↘*左边的项影响下边的项D员工←,↙*上边的项影响左边的项O雇主→,↖*下边的项影响左边的项R相关方

注：*一般箭头放在表示关系强弱的符号旁边。

日常工作中，最常用的是L型矩阵图。但实践中的问题并不都是那么简单，应结合工作实际考虑采用哪种形式的矩阵更能清楚地揭露数据的含义及其之间的关系。

矩阵图相关性符号的使用

为了在矩阵图中清晰明了地表达因素之间的关系，还需要用符号表示更丰富的信息。一般用X表示“是”、空格表示“否”的关系，还有如相关性存在或不存在、包括或不包括、适用或不适用等。可以说明的信息一般有两类：(1)两项之间的相关性强弱；(2)如果矩阵中的两项是人和活动，则可以说明人在活动中扮演的角色。

表2是矩阵图的常用符号。还可以自己设置便于别人识别的符号和字母，并标注说明。

矩阵图的制作步骤

矩阵图的制作一般遵循以下步骤：

(1)列出质量因素。可将因素细化分为子因素，或者将因素分类分组。可采用QC新七种工具中的KJ法。

(2)把各个因素组排列成行和列，分析各个因素组之间的对应关系。

(3)选择合适的矩阵图。

(4)在成对的因素交点处标注它们之间的关系程度。可以凭经验进行定性判断，如关系密切、关系较密切、关系一般(或可能有关系)，采用不同符号表示，无关系则不标注；也可采集数据进行相关性分析，予以量化表示。

(5)根据关系严重程度确定必须控制的重点因素。

(6)针对重点因素制定相应对策或解决方案。

案例分析

有效的心理护理要求护理人员运用心理学的理论和方法,通过设计的语言和行为(合理的解释、善意的劝导、真诚的抚慰、有益的暗示、确切的保证等)，实现对患者的心理调控、心理支持或心理健康教育过程。在护理过程的每一个环节中,护理人员一切言谈举止对患者的心理状态都有影响。研究表明[1]，非A型性格护士对乳癌患者实施心理护理后效果相对较好，这种差异主要来自于强迫症状因子、抑郁因子、焦虑因子。A型性格中的部分优秀品质，如做事利索、工作投入、要求严格、说话直率等有利于提高工作效率。临床管理者只要注意发挥护士性格中有利的一面,克服不利的一面，取长补短,培养护士良好的习惯和性格,就一定能更好地发挥团队力量，不断提升护理质量。采用矩阵图，可以分析语言和行为与患者的心理调控、心理支持或心理健康教育过程的相关性，及非A型性格护士中的强迫症状因子、抑郁因子、焦虑因子。