基于支持向量机的压电微操作平台非线性特性描述
胡俊峰 郑昌虎 蔡建阳
江西理工大学,赣州,341000
基于支持向量机的压电微操作平台非线性特性描述
胡俊峰 郑昌虎 蔡建阳
江西理工大学,赣州,341000
压电驱动器的迟滞现象会使微操作平台出现非线性问题,严重影响了其运动精度和重复定位精度。为了解决该问题,提出了一种基于Preisach模型与支持向量机的联合建模方法来描述微操作平台的非线性特性。以一种一维微操作平台为对象,以压电驱动电压和所对应的平台输出位移为样本点,采用支持向量机理论建立反映平台非线性回归模型,利用该模型预测非样本点所对应的平台输出位移,结合Preisach模型可精确预测平台在任意电压序列作用下的输出位移。为了验证所建立模型的有效性,进行了实验研究,任意选取2组不同的输入电压序列,利用支持向量机回归模型和Preisach模型分别得到所选取的电压序列对应的输出位移的预测值,在相同的电压序列作用下进行实验得到其实测值,将实测值与预测值进行比较分析,结果表明,2组实测值与预测值之间的相对误差范围分别为0.6%~2.1%、0.02%~2.1%,预测位移与实测位移非常接近,说明所建立的模型能精确描述微操作平台的非线性特性,以实现其精确运动。
微操作平台;压电驱动器;Preisach模型;支持向量机;非线性特性
0 引言
目前,高精度、高分辨率的精密微操作平台在精密定位、微机械操作、医疗器械、超精密加工、航空航天等前沿领域应用越来越广泛[1-2]。柔顺机构是利用柔性铰链的弹性变形传递运动和力的一种新型免装配机构。柔顺机构具有无摩擦、无间隙、分辨率高和加工简单等优点,特别适宜作为微操作平台机构[2]。压电陶瓷驱动器(PZT)具有刚度高、响应速度快、功耗低、输出力大等优点[3-6],PZT和柔顺机构结合而成的微操作平台具有广泛应用前景。但是,压电驱动器在电场作用下会出现迟滞现象,使其具有多值映射性和记忆性等非线性特性,使得微操作平台出现非线性问题,致使其重复精度降低,严重影响平台的控制精度。目前,微操作平台的模型仅考虑了柔顺机构的力学模型,没有考虑压电驱动器的非线性特性对平台性能的影响,因此,需要建立能反映压电驱动器迟滞非线性特性对平台影响的模型,以便基于该模型对平台进行精确位移控制。
为了建立反映迟滞非线性特性的模型,国内外学者提出了Maxwell滑动模型[3]、Duhem模型[4]、Prandtl-Ishlinskii模型[5]和Preisach模型[6-9]等。但是这些模型仅用于反映压电驱动器的非线性,没有应用于压电微操作平台。其中,Preisach模型是目前应用广泛的描述非线性现象的模型之一,它具有原理清晰、结构简单、精度高、易于和控制方法相结合等优点。但是,建立能精确反映迟滞非线性的Preisach模型的关键是对迟滞环进行回归拟合,目前建立回归模型的方法主要有神经网络[7-9]、模糊算法[10]、滑模算法[11]和插值算法[12-14]等。但是,采用以上建模方法均需要较大的样本数据量,由于小样本数据量会造成神经网络建模过程中出现“过拟合”现象和模糊算法的模糊规则不清等问题,滑模算法增加了Preisach模型的复杂性。支持向量机可以解决采用小样本数据回归非线性拟合问题[15],所以支持向量机回归理论适合于建立压电微操作平台的非线性模型。同时,支持向量机从结构风险最小化的角度保证了模型的最大泛化能力,根据该理论建立的模型能精确预测驱动器在任意输入电压所对应的平台输出位移。
本文以一种一维微操作平台为对象,采用Preisach模型和支持向量机联合建模的方法描述由压电陶瓷驱动器迟滞现象所引起的微操作平台的非线性特性。首先,建立反映微操作平台非线性特性的离散化形式的Preisach模型;然后,采用支持向量机理论建立反映压电驱动器电压与所对应的平台输出位移之间非线性关系的回归模型,根据该模型可预测任一电压所对应的输出位移,从而根据Preisach模型计算出压电驱动器任意输入电压系列的对应的平台输出位移;最后,进行实验验证分析,以证明所提出方法的可行性和有效性。
1 压电微操作平台的Preisach模型
图1所示为一维微操作平台[2],由于压电驱动器的迟滞现象会使平台出现图2所示的非线性特性,图2中(αi,βi)为施加在压电驱动器第i个电压极值点(i=1,2,…,n;αi≥βi),当αi>βi时,(αi,βi)表示电压从0上升αi后再下降到βi,x(αi,βi)为此时平台的输出位移,由图2可知,在相同电压驱动下平台的输出位移不相同,取决于施加电压顺序。f(αi,βi)为驱动器电压从0上升至αi后下降至βi时的位移变化量,它可表示为
f(αi,βi)=x(αi,αi)-x(αi,βi)
(1)

图1 微操作平台
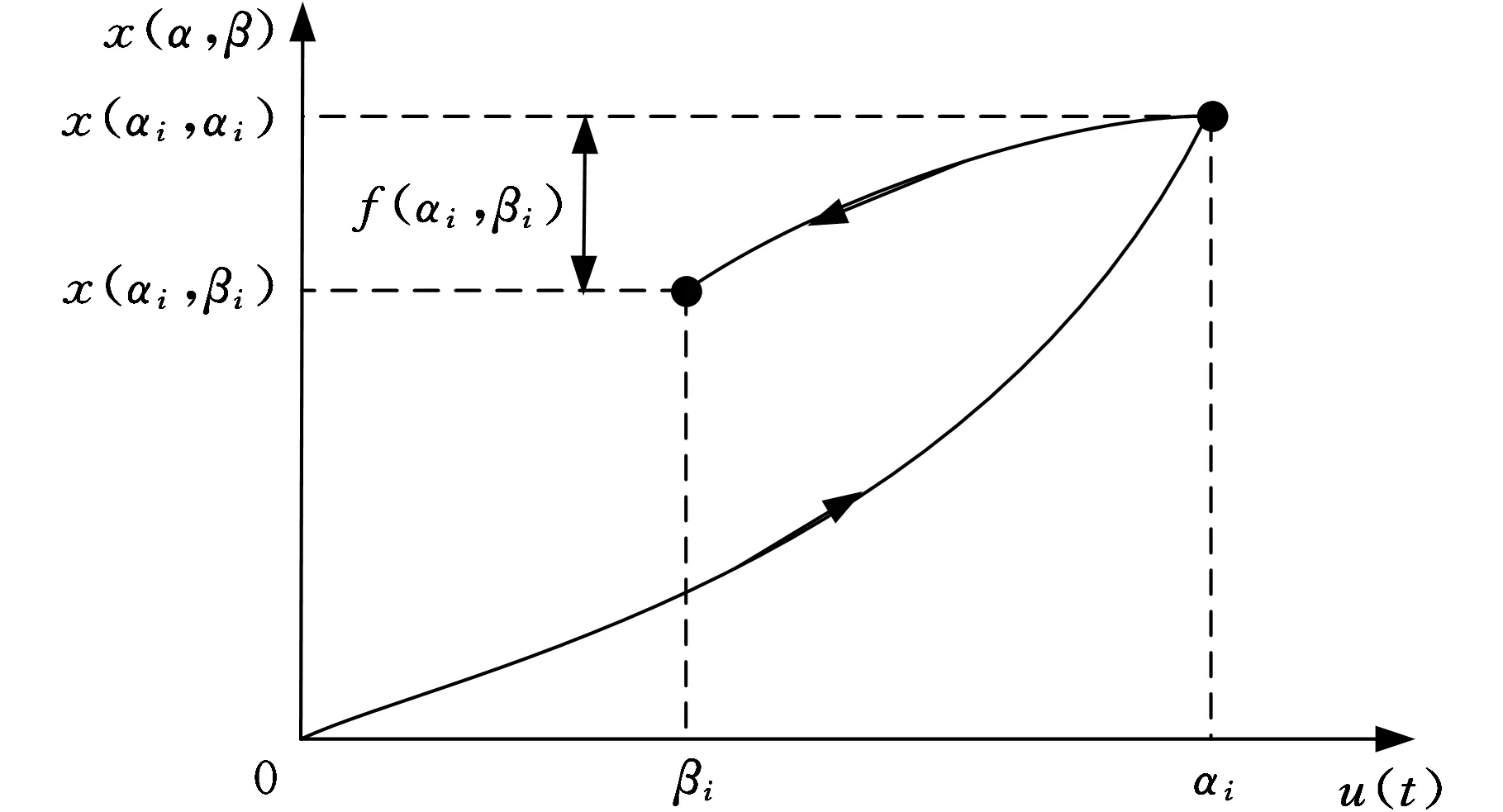
图2 微操作平台的非线性特性
图2所示的非线性可采用Preisach模型描述,图2中箭头朝上的曲线为电压上升阶段,箭头朝下的曲线为电压下降阶段,离散化Preisach模型[12]可表示为
(2)
式中,u(t)、f(t)分别为压电驱动器在t时刻的输入电压和平台的位移输出值;n为饱和电压的等分个数。
由式(1)和式(2)可知,欲求出在t时刻的输出位移f(t),需要获得x(αi,βi)。通过实验得到x(αi,βi)的过程如下:首先将压电陶瓷驱动器的饱和电压U平均分为n等分,每个等分点的电压值为kU/n(k=1,2,…,n),将压电陶瓷驱动器的电压从0上升至任一等分点kU/n,记下此时的电压(kU/n,kU/n)和平台输出位移x(kU/n,kU/n);然后,将电压下降到0,记下下降过程中经过的等分点上的电压(kU/n,mU/n)和平台输出位移x(kU/n,mU/n),m=k-1,k-2,…,1。遍历所有等分点,可以得到压电陶瓷驱动器在等分点上的电压与所对应的位移。
现通过一实例说明上述模型,设压电驱动器的饱和电压为60 V,将其均分为3等分,等分点电压分别为0、20 V、40 V、60 V,如图3所示。将压电驱动器的电压从0上升至60 V,记下此时极值电压(60,60)和输出位移x(60,60),然后将电压从60 V下降至0,记下下降过程经过的等分点电压极值点(60,40)、(60,20)、(60,0)和相应的平台输出位移x(60,40)、x(60,20)、x(60,0)。同理,将电压从0上升至40 V再降到0,得到x(40,40)、x(40,20)和x(40,0)。最后将电压上升至20 V再减为0,得到x(20,20)与x(20,0)。
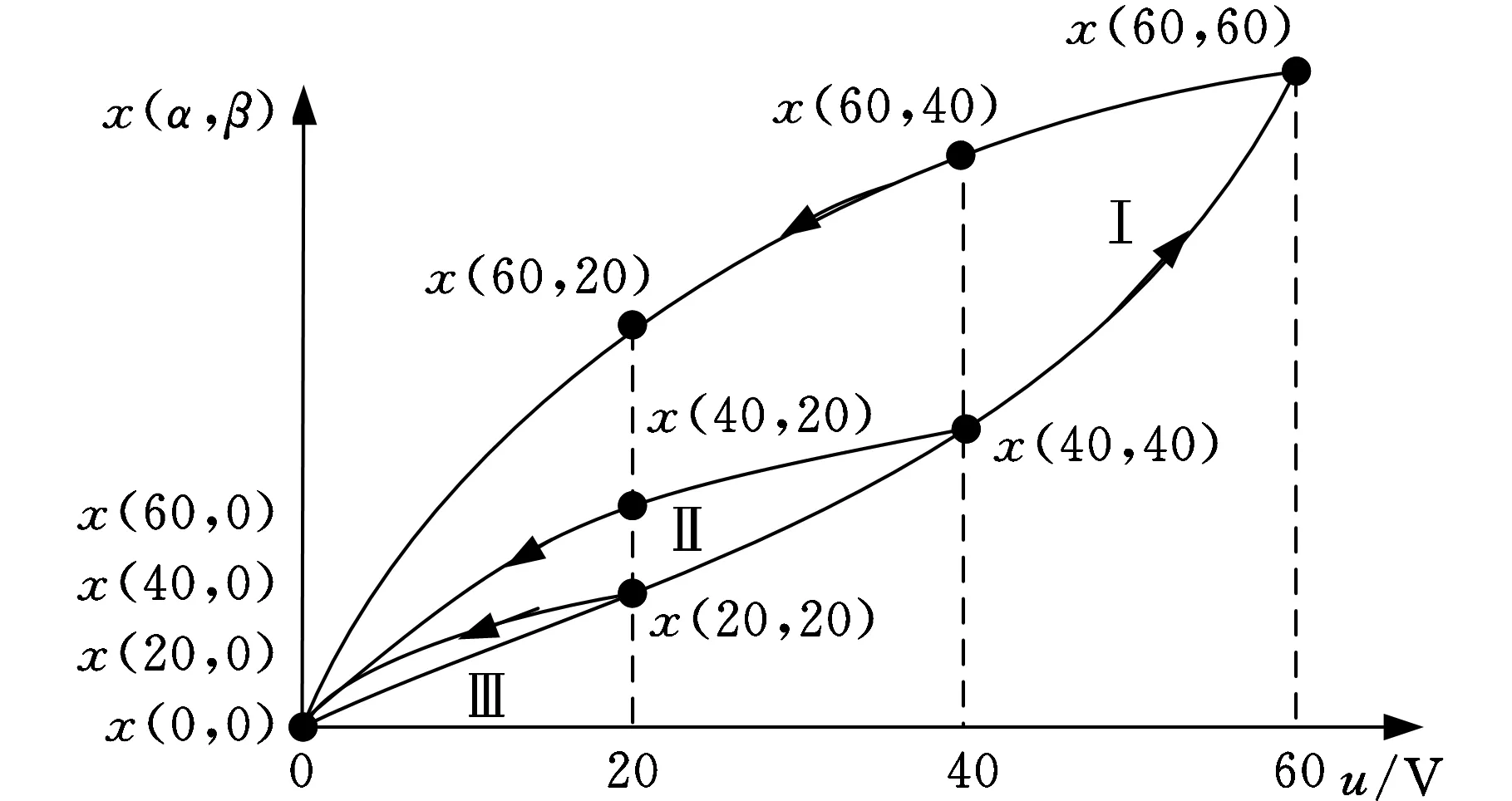
图3 说明Preisach模型的实例
由图3可知,对压电陶瓷驱动器施加的电压都在等分点上,可以得到各电压对应的输出位移。设压电驱动器输入0-60 V-20 V-40 V的序列电压,其极值点电压均在等分点上,根据式(2)计算平台输出位移的步骤如下:
(1)根据施加电压的顺序可确定α1= 60 V,α2= 40 V,β0= 0,β1= 20 V,β2= 0,u(t)= 20 V。
(2)当i=1时,由式(2)可得
f(α1,β0)-f(α1,β1)=f(60,0)-f(60,20)=
[x(60,60)-x(60,0)]-[x(60,60)-x(60,20)]
(3)
(3)当i=2时,由式(2)可得
f(α2,β1)-f(α1,β2)=f(40,20)-f(40,0)=
[x(40,40)-x(40,20)]-[x(40,40)-x(40,0)]
(4)
(4)由式(2)可计算
f(u(t),β2)=f(20,0)=x(20,20)-x(20,0)
(5)
(5)微操作平台的输出位移为
x(60,20)-x(60,0)+x(40,0)-
x(40,20)+x(20,20)-x(20,0)
(6)
根据上述求解过程,当输入电压序列均在等分点上时,可以通过直接利用在等分点上的x(α,β)计算压电驱动器所对应的平台输出位移。但是,当电压不在等分点上时,例如当压电驱动器输入电压顺序为0-50 V-30 V-45 V-0-10 V,利用式(2)计算其输出位移为x(50,30)-x(50,0)+x(45,0)-x(45,30)+x(10,10)-x(10,0)。但各x(α,β)无法得到,可采用支持向量机建立反映图3所示的输出位移x(α,β)与输入电压(α,β)之间关系的迟滞环Ⅰ、Ⅱ、Ⅲ的回归模型,然后根据该模型预测任一点的x(α,β)值,从而根据式(2)计算出平台的输出位移。
2 基于支持向量机的非线性模型
为了建立反映微操作平台非线性回归模型,等分点上驱动器的输入电压与平台输出位移构成支持向量机的样本点{[(α1,β1),x1(α1,β1)],…,[(αm,βm),xm(αm,βm)]},m为样本点数。由于输出位移x(α,β)与输入电压(α,β)之间关系为非线性,采用支持向量机理论通过非线性映射函数将由不同输入电压顺序的(α,β)形成的输入样本空间映射到高维特征空间,在高维特征空间构造反映微操作平台非线性的回归函数为
f(z)=ω·φ(z)+b
(7)
式中,ω为超平面系数;z为某迟滞环对应的电压(α,β);b为待定偏置量;φ()为未知的高维函数;ω·φ(z)为ω与φ(z)的内积;f(z)为x(α,β)。
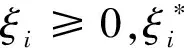
(8)
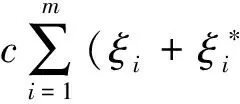

(9)
其中,R(zi,zk)表示核函数,R(zi,zk)=φ(zi)·φ(zk),即φ(zi)与φ(zk)的内积,选取径向基(RBF)核函数,它可表示为
R(z,zi)=exp(-g‖z-zi‖2)
(10)
式中,g为核函数的宽度参数。

(11)
偏置量b可通过Karush-Kuhn-Tucker条件求得
(12)
联立式(7)、式(11)和式(12)可得反映微操作平台非线性的回归函数:
(13)
为了衡量式(13)所示的回归模型的精度,采用平方相关系数进行评价,它可表示为
r2=
(14)
式中,k为测试点数;f(zi)、yi分别为第i个测试点的预测位移和实测位移。
由支持向量机理论[16]可知,惩罚系数c和核函数宽度参数g对能否建立精确反映微操作平台非线性模型具有重要作用。惩罚系数c用于权衡所建立的模型复杂度和精度,由式(8)可知,系数c越大,对样本点的拟合程度越高,模型复杂度高,所建立的反映平台非线性的模型泛化能力变差;系数c越小,对样本点数据中超出模型与实际输出位移的误差要求ε的样本惩罚越小,使训练误差变大,建立模型的精度不高[15]。核函数宽度g与样本点的输入空间范围有关,样本点越多取值越大,反之取值越小。所以,需要根据实验样本点优化选择合适的系数c和g,以建立能精确预测在不同驱动电压所对应的输出位移。
目前对参数c和g优化的方法主要有梯度法、粒子群法等,相比这些优化方法,栅格化搜索方法的优点是迭代搜索简单,能同时搜索多个参数并保证其在划分网格中的全局最优解,便于并行计算,运行效率高,所以采用栅格搜索方法寻找能精确建立平台回归模型的最优参数c和g。
由于通过位移传感器采集的样本点数据具有随机误差,该误差会影响参数(c,g)的性能评价,对于同一组(c,g),拟合函数的精确性会随样本数据变化而变化,尤其对于小样本数据,样本数据的随机性对参数优选的影响较大,不利于模型的推广。因此,在栅格搜索过程中应用交叉验证法对每组参数组合的性能进行综合评价。将交叉验证与栅格搜索方法相结合,以均方误差的均值最小为目标对参数c与g进行优选,以提高参数优选的效率和准确性,消除样本数据的随机误差对平台回归模型精确性的影响。
采用栅格搜索与交叉验证相结合的方法对参数(c,g)的寻优过程如图4所示,具体步骤如下。
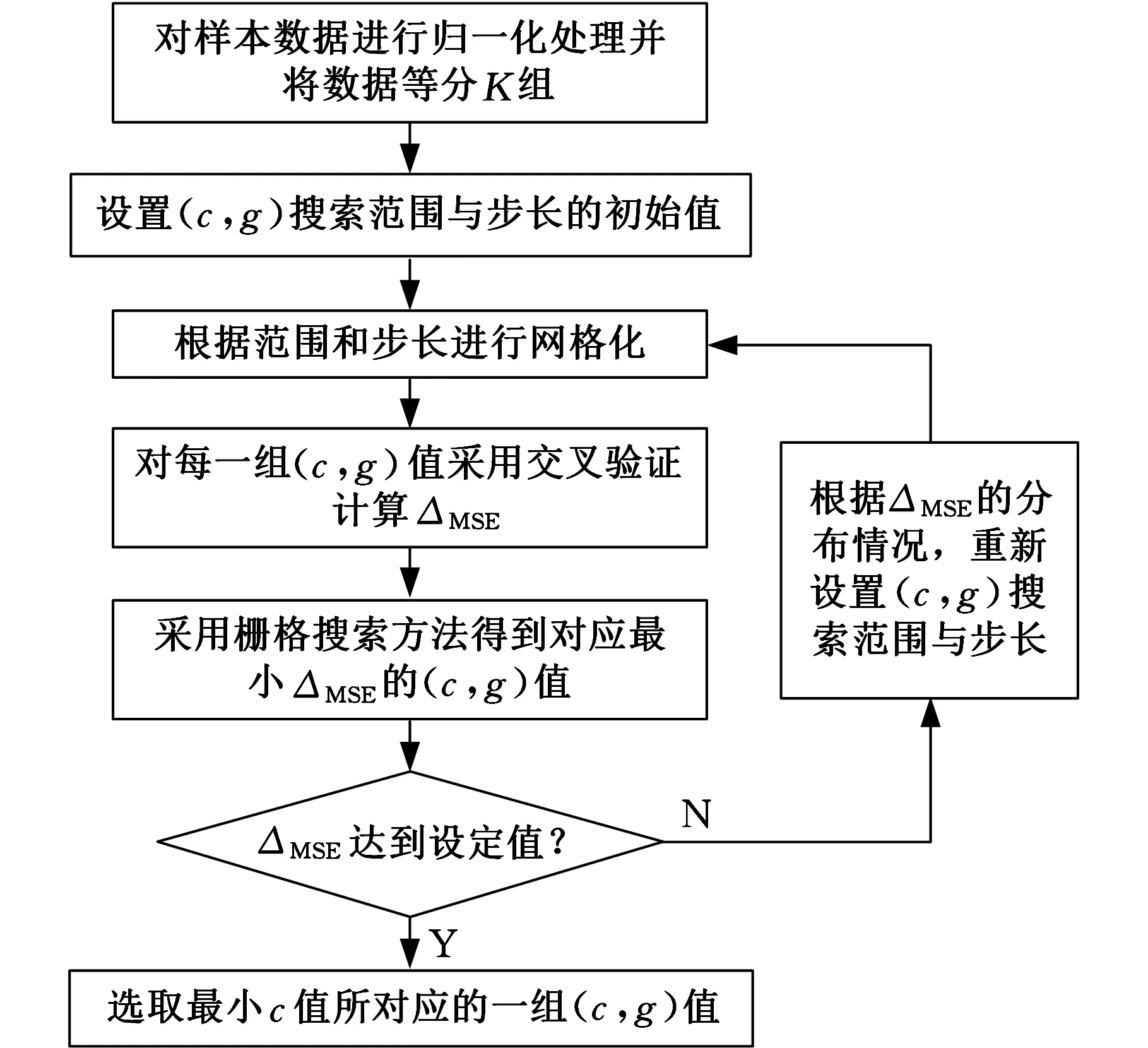
图4 参数(c,g)的寻优流程

(15)
(2)设置(c,g)的搜索范围和步长,由于初始无法估计c与g的大致范围,搜索范围应尽可能大,所以采用对数坐标形式(log2c,log2g)对其进行栅格化。
(3)将训练数据等分为K组(K≥2),对于栅格中每一组(c,g),以任意一组作为测试组,其余K-1组作为训练组,训练模型后对测试组进行预测,并计算这一组(c,g)对应的均方误差,其定义为
(16)
式中,f(xi)为预测值;yi为样本实际值。
(4)对于与步骤(3)相同的(c,g),更换另一测试组,取剩余K-1组作为训练集,根据式(16)计算均方误差,直至对K组都进行一次预测后,取K组均方误差的均值ΔMSE作为该组(c,g)的预测误差。
(5)更换参数组合(c,g),重复步骤(3)和(4),逐次计算网格中各参数组合(c,g)下的均方误差,对所有的组合的ΔMSE进行比较,ΔMSE最小的参数组合即网格区间内的最佳(c,g)值。
(6)判断ΔMSE是否小于Δmin,若是则结束流程;否则根据ΔMSE的分布情况,缩小参数搜索范围和步长,重复步骤(3)~(5)直至满足要求。
3 实验验证
3.1 实验装置

图5 实验装置
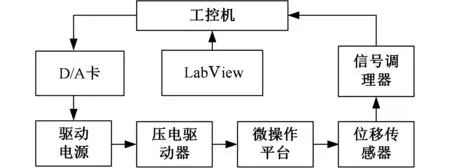
图6 实验数据采集过程
如图5所示,实验装置由微操作平台、压电陶瓷驱动器、驱动电源、位移传感器、信号调理器、D/A卡、工控机等组成。压电驱动器为哈尔滨芯明天公司生产的80VS12,电压取值范围为0~150 V;驱动电源为芯明天公司生产的XE-501,功率放大倍数为15;位移传感器为PI公司生产的D-E20.200,分辨率为0.2 μm,线性度为0.3 %;D/A卡为NI公司生产的PCI-6713。实验样本数据点采集过程如图6所示,根据第1节所述的施加电压顺序,采用LabView软件编写电压输入程序,通过D/A卡将工控机输出的电压经功率放大作为压电驱动器的输入电压,采用位移传感器测量所对应的输出位移,位移信号经信号调理器通过USB接口输入至工控机,采用LabView编写位移采集程序,以获得对应各个电压等分点的输出位移。
3.2 微操作平台的非线性模型的实验验证
由于合适的参数(c,g)对于能否建立精确反映微操作平台非线性模型非常关键,下面通过拟合平台外环曲线来说明栅格搜索和交叉验证方法找寻(c,g)值的有效性。由于VS80型压电驱动器的输入电压超过120 V会影响其使用寿命,故将驱动器的饱和电压设为120 V。为了拟合平台的外环曲线,将饱和电压等分为40个点,并测量该等分点对应的输出位移得到样本数据点,见表1。
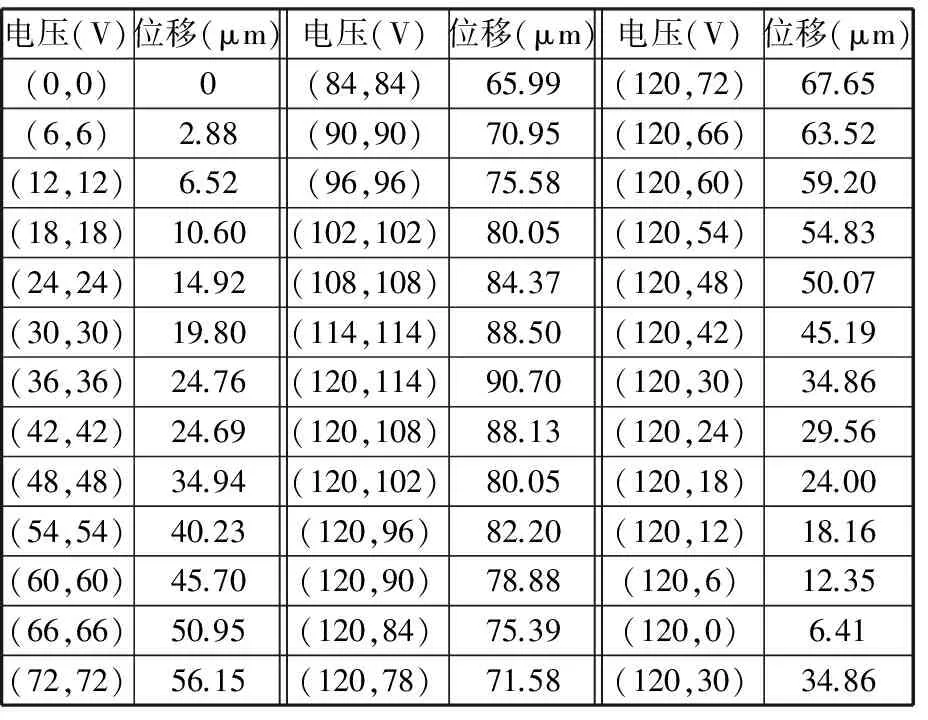
表1 用于拟合微操作平台外环曲线的样本点
c与g的初始寻优范围为[2-10,210],寻优步长设为2-1,K=3,ε=0.001,Δmin=10-4μm2。图7所示为c和g寻优范围内每个栅格对应的ΔMSE值,图8所示为对应的ΔMSE值等高线。由图7和图8可看出ΔMSE的变化趋势,ΔMSE接近于0的c与g的范围如图8中虚线部分所示,在该范围内ΔMSE值均小于Δmin,在该范围内寻优选取最小的c值所对应的一组(c,g),可得到c=32,g=1.4,ΔMSE=2.3625×10-6μm2。根据该(c,g)值可拟合出描述平台外环的回归曲线,如图9所示。
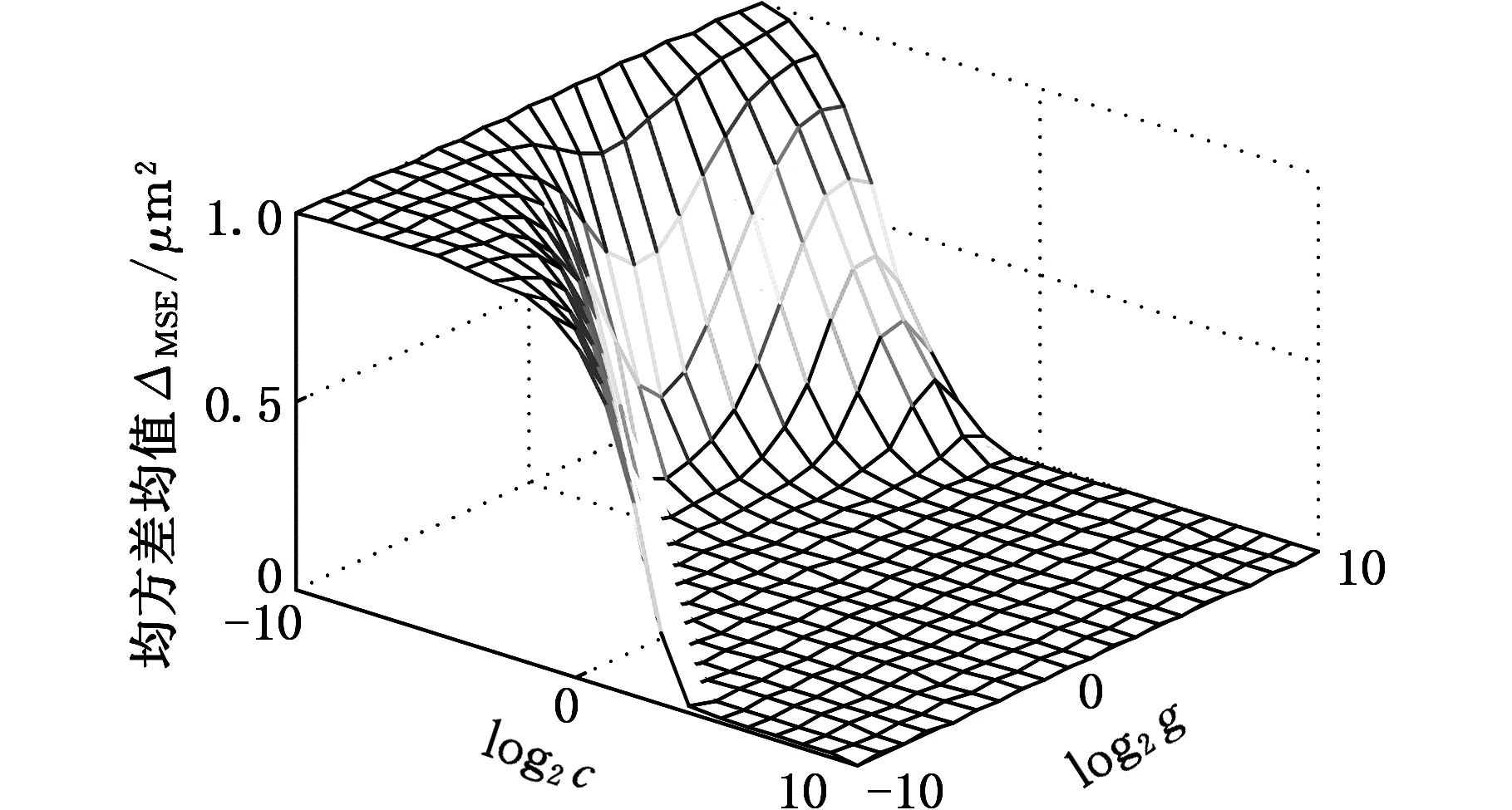
图7 均方差均值的分布

图8 均方差均值的等高线
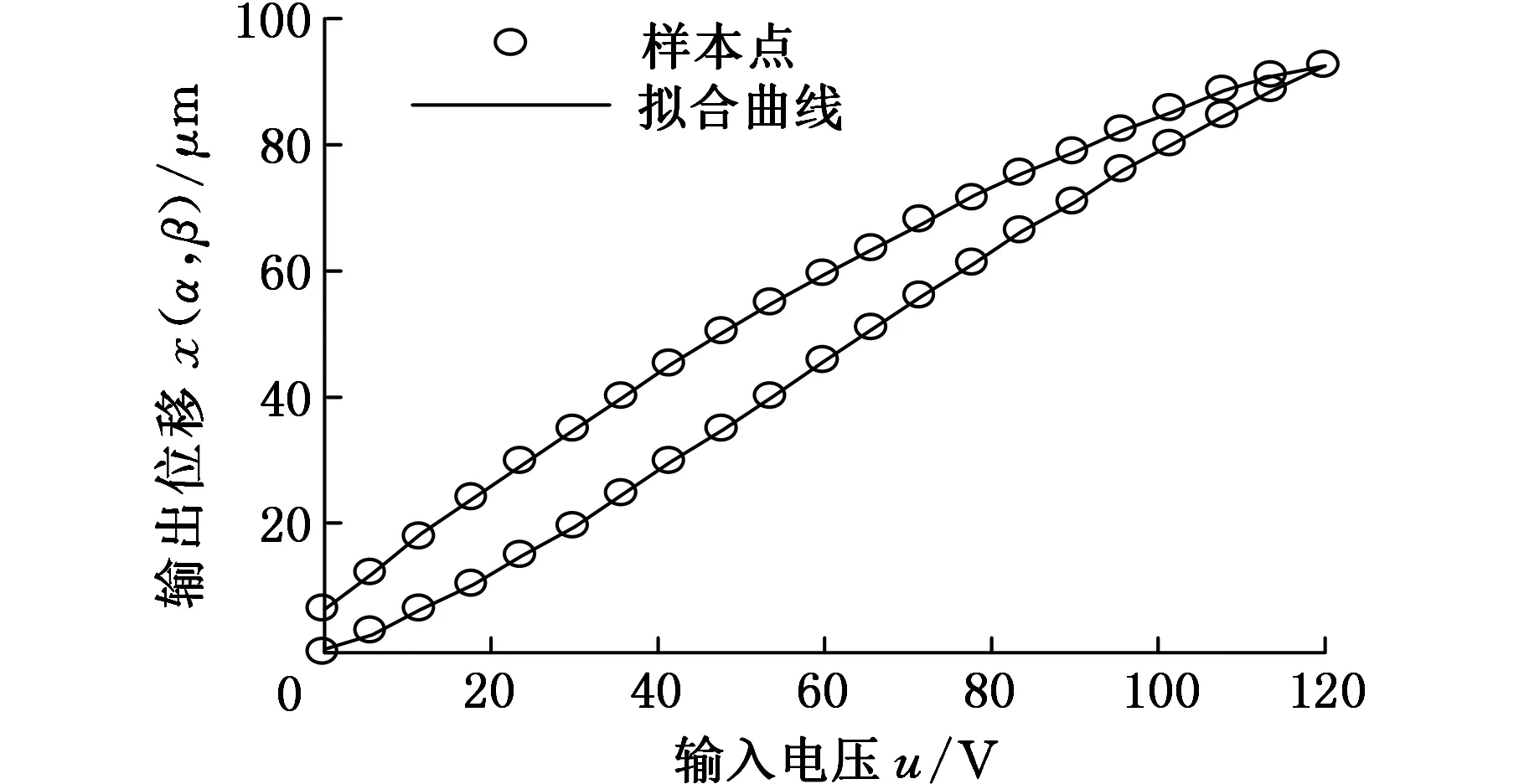
图9 微操作平台外环的拟合曲线
为了说明回归曲线的精确性,选取12个测试样本点进行验证分析,测试样本点包括外环上升曲线的6组点与下降曲线的6组点,见表2。
图10所示为12个测试点的实测位移与由模型得到的预测位移之间的误差,由图10可知,误差值范围为[-0.15,0.15]μm。同时,将12个测试点的实测位移与预测位移分别代入式(14)和式(16),可分别得到衡量回归曲线精度的指标r2=0.999 99和EMS=9.504×10-7μm2,由该指标可知平台的外环曲线拟合度较好,说明交叉验证的栅格搜索方法能确定合适的(c,g)值以建立精确反映平台非线性模型。
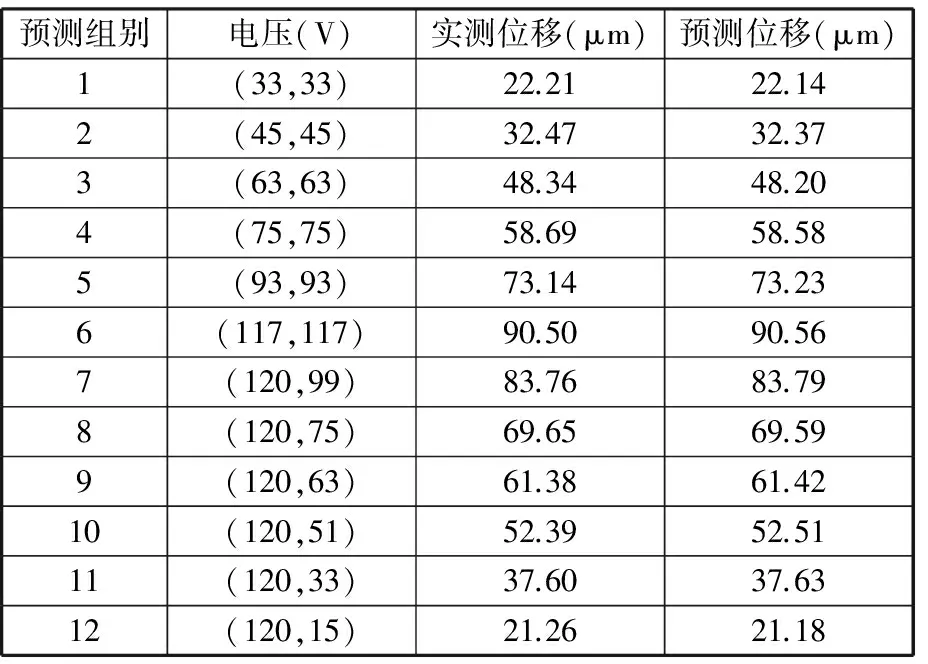
表2 测试点和对应的位移预测值与实测值
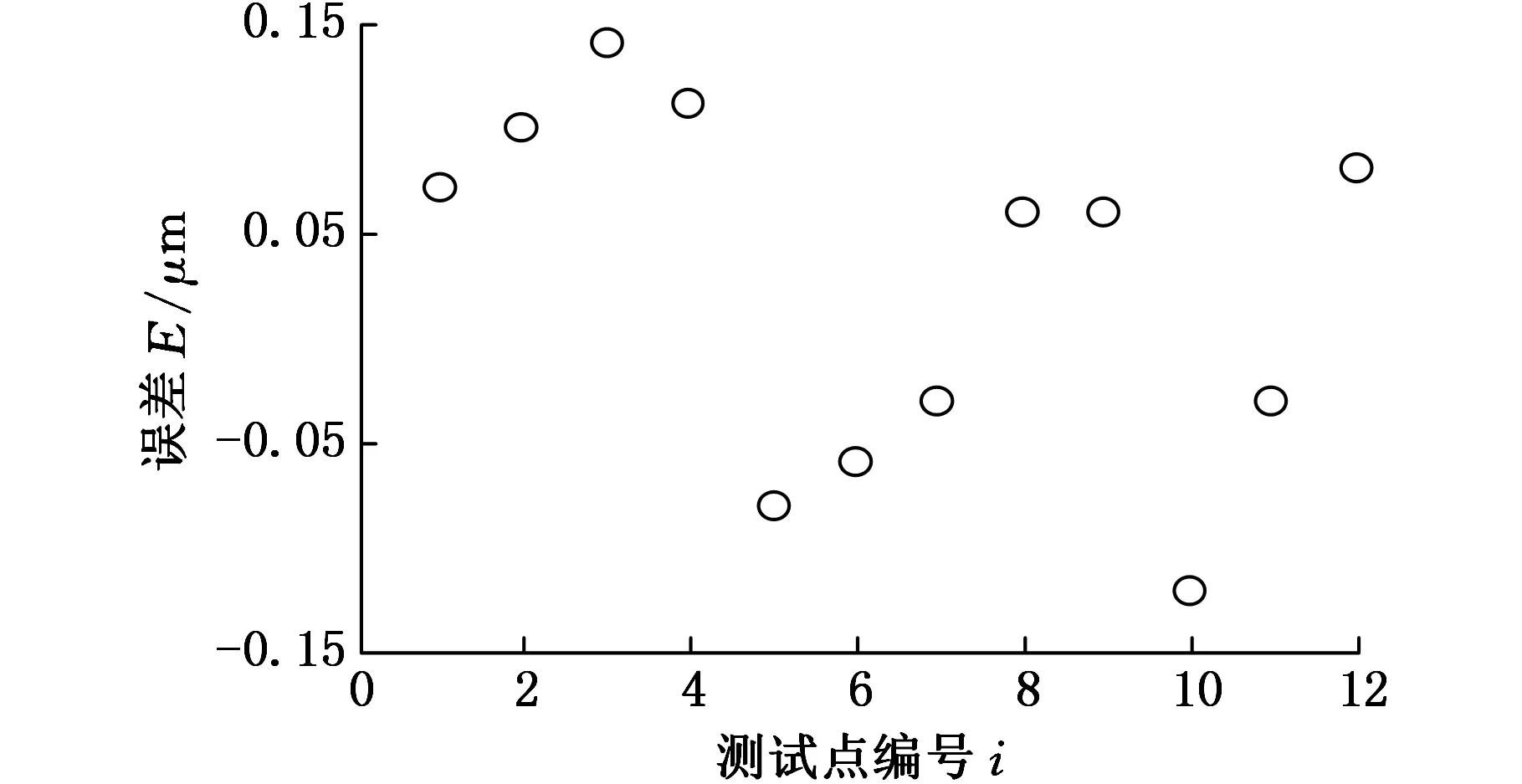
图10 误差分布
下面通过实验验证分析采用支持向量机和Preisach模型描述微操作平台非线性的有效性。将压电驱动器的输入电压分成16等分,得到等分点上的极值点电压(α,β)和平台对应的输出位移x(α,β)构成的样本点,见表3。设c与g的寻优范围为[2-10,210],步长设为2-1,K = 4,ε= 0.001,Δmin=10-5μm2。根据图3所示流程可得到最优(c,g)值组合,即c = 32,g = 4,该组合对应的均方误差的均值ΔMSE=1.485×10-6μm2,说明(c,g)值能满足设定的要求。根据该参数组合采用支持向量机对表3中的样本点进行训练,得到图11所示的回归曲线,该曲线反映了平台的非线性特性。根据式(14)可计算出反映曲线拟合精度的指标r2=0.999 986,说明所拟合的曲线能精确地反映平台的非线性特性。

图11 微操作平台的拟合曲线
为了验证分析运用Preisach模型和支持向量机所建立的模型能预测不同输入电压序列的输出位移,可通过比较分析当压电驱动器在不同输入电压序列作用下的平台输出位移的实际值与预测值来实现。选取第1测试组为极值点位于等分点上的电压序列0-120 V-60 V-75 V-15 V-105 V,第2测试组为极值点不在等分点上的电压序列0-112.5 V-19.5 V-69 V-36 V-93 V-68 V。由式(1)和式(2)表示的Preisach模型可知,要计算出电压序列的输出位移,需要得到不同输入电压(α,β)所对应的位移x(α,β),可利用图11所示的回归模型得到x(α,β),第1和第2测试组各输入电压对应的位移x(α,β)分别见表4和表5。
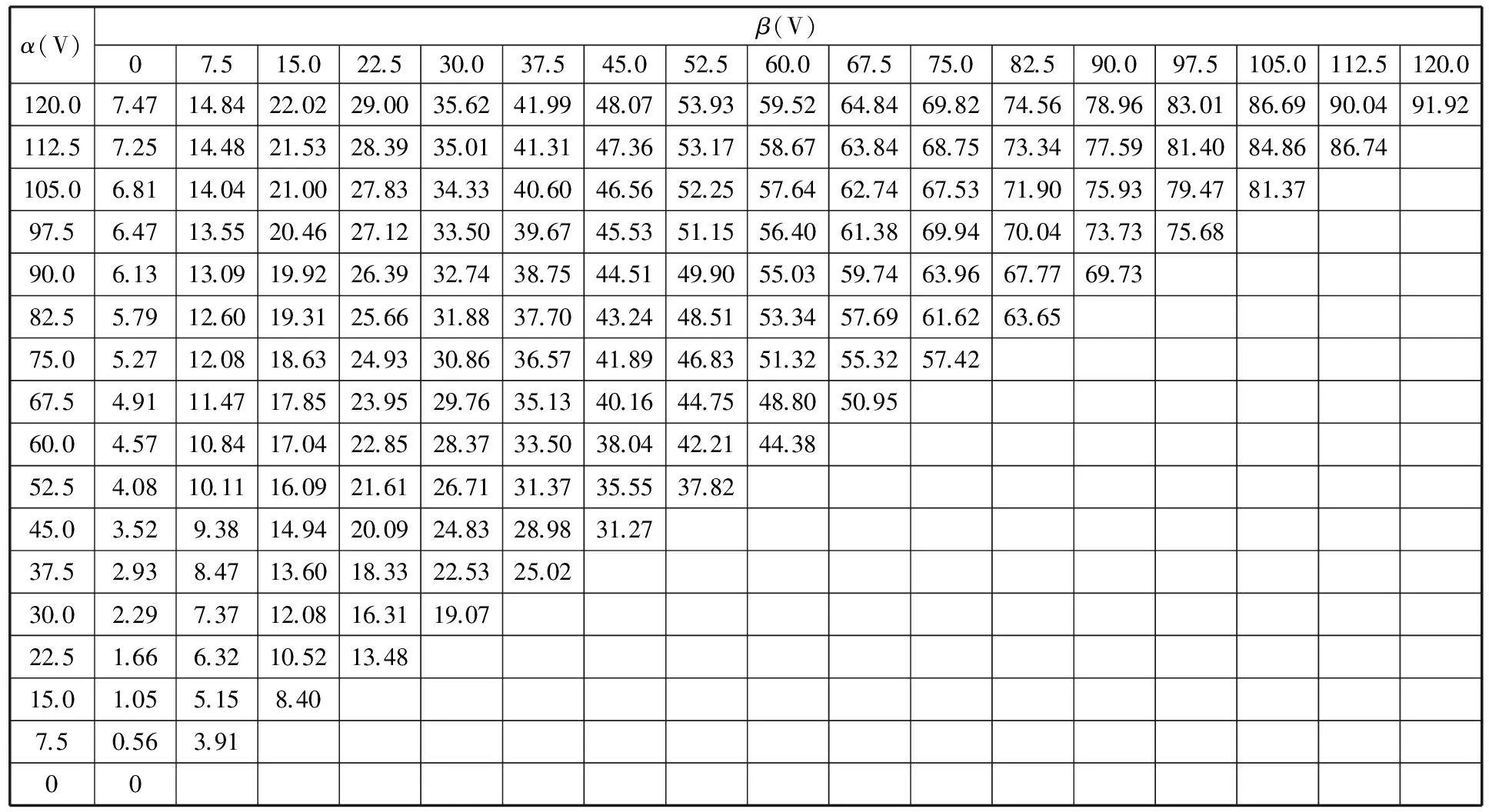
表3 用于拟合微操作平台迟滞环的样本点 μm
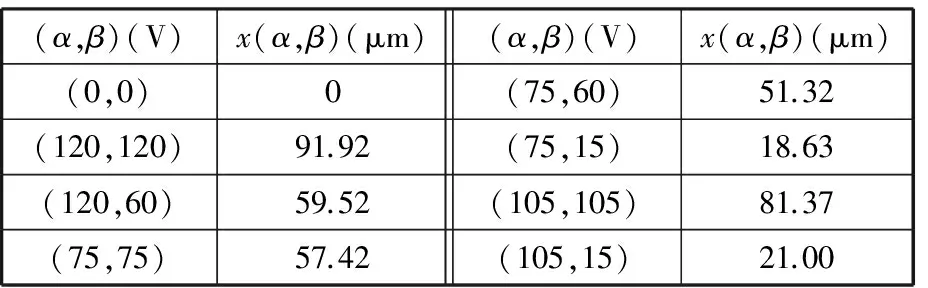
表4 第1测试组电压对应的x(α,β)预测值
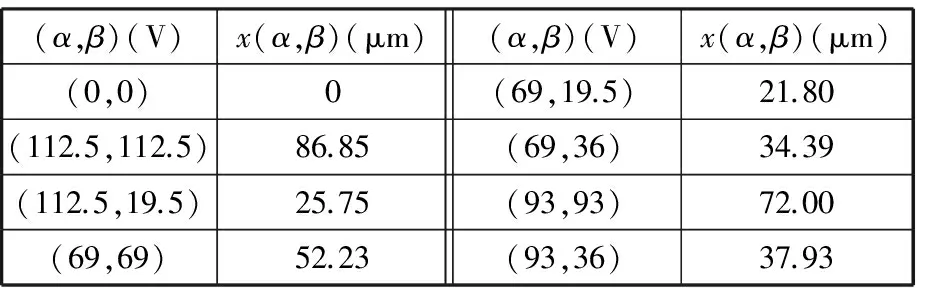
表5 第2测试组电压对应的x(α,β)预测值
根据表4和表5中的x(α,β),将其代入式(1)和式(2)表示的Preisach模型,则可以分别计算出对应于两组测试组各电压序列的输出位移f(z)的预测值。根据图5所示的实验过程,对压电陶瓷驱动器分别施加上述两组序列电压,可以分别得到不同输入电压所对应的输出位移的实测值。第1和第2测试组的各输入电压对应的输出位移的实测值、预测值、相对误差分别见表6和表7,可知,第1和第2测试组的相对误差范围分别为0.6%~2.1%和0.02%~2.1%,说明预测位移与实测位移非常接近,也就是说,联合Preisach模型和支持向量机回归模型能精确预测平台在驱动器输入任意电压序列所对应的输出位移,从而实时预测平台的输出位移。
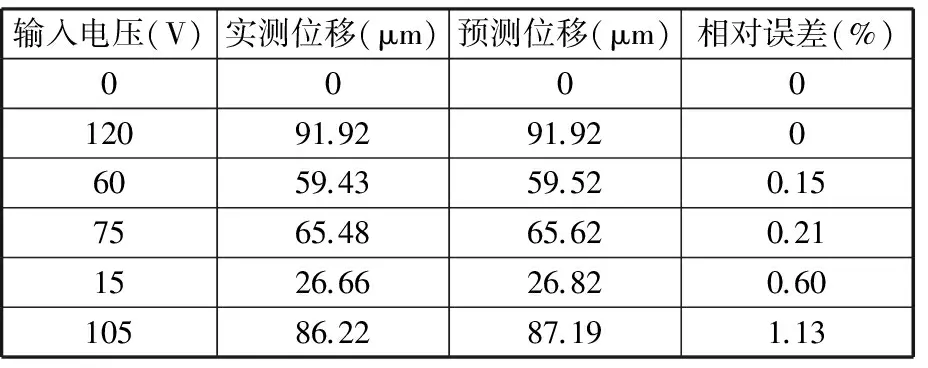
表6 第1测试组的实测位移和预测位移

表7 第2测试组的实测位移和预测位移
4 结语
为了精确描述压电微操作平台非线性特性,本文提出了一种Preisach模型与支持向量机回归方法相结合的建模方法。提出了一种基于交叉验证和栅格化搜索方法,对非线性模型精度有较大影响的惩罚系数c与核函数参数g进行寻优。以一种一维微操作平台为对象,利用支持向量机回归理论拟合的非线性回归曲线,并结合传统的Preisach模型,可对任意输入电压系列的平台输出位移进行精确的预测。实验验证分析结果表明,基于交叉验证的栅格搜索方法能确定合适的(c,g)值以建立反映平台非线性的精确回归模型,联合Preisach模型能精确预测任意输入电压序列的输出位移,说明所建立的模型能精确描述微操作平台的非线性特性,以实现其精确运动。
[1]YueYi,GaoFeng,ZhaoXianchao,etal.RelationshipamongInput-force,Payload,StiffnessandDisplacementofa3-DOFPerpendicularParallelMicro-Manipulator[J].MechanismandMachineTheory, 2010, 45(5):756-771.
[2] 胡俊峰, 徐贵阳, 郝亚洲.基于响应面法的微操作平台多目标优化[J].光学精密工程, 2015, 23(4):1096-1104.HuJunfeng,XuGuiyang,HaoYazhou.Multi-objectiveOptimizationofaNovelMicro-manipulationStageBasedonResponseSurfaceMethod[J].OpticsandPrecisionEngineering, 2015, 23(4): 1096-1104.
[3]VominhT,TjahjowidodoT,RamonH,etal.ANewApproachtoModelingHysteresisinaPneumaticArtificialMuscleUsingtheMaxwell-slipModel[J].IEEE/ASMETransactionsonMechatronics, 2011, 16(1): 177-186.
[4]LinCJ,LinPT.TrackingControlofaBiaxialPiezo-actuatedPositioningStageUsingGeneralizedDuhemModel[J].Computers&MathematicswithApplications, 2012, 64(5): 766-787.
[5]JiangH,JiH,QiuJ,etal.AModifiedPrandtl-ishlinskiiModelforModelingAsymmetricHysteresisofPiezoelectricActuators[J].IEEETransactionsonUltrasonicsFerroelectrics&FrequencyControl, 2010, 57(5): 1200-1210.
[6]XiaoShunli,LiYangmin.ModelingandHighDynamicCompensatingtheRate-dependentHysteresisofPiezoelectricActuatorsviaaNovelModifiedInversePreisachModel[J].IEEETransactionsonControlSystemsTechnology, 2013, 21(5): 1549-1557.
[7]MohammadRZ,MohsenF,HassanS,etal.HysteresisNonlinearityIdentificationUsingNewPreisachModel-basedArtificialNeuralNetworkApproach[J].JournalofAppliedMathematics, 2011, 2011(22):1-21.
[8] 刘向东, 修春波, 李黎,等.迟滞非线性系统的神经网络建模[J].压电与声光, 2007, 29(1): 106-108.LiuXiangdong,XiuChunbo,LiLi,etal.HysteresisModelingUsingNeuralNetworks[J].Piezoelectectrics&Acoustooptics, 2007, 29(1): 106-108.
[9] 赵新龙, 谭永红.对Preisach类的迟滞非线性神经网络建模[J].控制理论与应用, 2006, 23(4): 581-585.ZhouXinlong,TanYonghong.ModelingPreisach-typeHysteresisNonlinearityUsingNeuralNetworks[J].ControlTheory&Applications, 2006, 23(4): 581-585.
[10] 张建华, 葛红宇, 李宏胜,等.压电致动器Preisach模型的模糊插值算法及实现[J].南京理工大学学报,2011, 35(6): 780-785.ZhangJianhua,GeHongyu,LiHongsheng,etal.FuzzyInterpolationAlgorithmandRealizationofPreisachModelforPiezoActuator[J].JournalofNanjingUniversityofScienceandTechnology,2011, 35(6):780-785.
[11] 赖志林, 刘向东, 耿洁,等.压电陶瓷执行器迟滞的滑模逆补偿控制[J].光学精密工程,2011,19(6):1281-1290.LaiZhilin,LiuXiangdong,GengJie,etal.SlidingModeControlofHysteresisofPiezoceramicActuatorBasedonInversePreisachCompensation[J].OpticsandPrecisionEngineering, 2011, 19(6): 1281-1290.
[12] 魏燕定, 陶惠峰.压电驱动器迟滞特性的Preisach模型研究[J].压电与声光, 2004, 26(5): 364-367.WeiYanding,TaoHuifeng.StudythePreisachModelofHysteresisinPiezoelectricActuator[J].Piezoelectrics&Acoustooptics, 2004, 26(5): 364-367.
[13] 李黎, 刘向东,王伟,等.压电陶瓷执行器迟滞特性的广义非线性Preisach模型及其数值实现[J].光学精密工程, 2007, 15(5): 706-712.LiLi,LiuXiangdong,WangWei,etal.GeneralizedNonlinearPresachModelforHysteresisNonlinearityofPiezoceramicActuatorandItsNumericalImplementation[J].OpticsandPrecisionEngineering,2007,15(5):706-712.
[14] 陈辉, 谭永红, 周杏鹏,等.压电陶瓷执行器的动态模型辨识与控制[J].光学精密工程, 2012, 20(1):88-95.ChenHui,TanYonghong,ZhouXingpeng,etal.IdentificationandControlofDynamicModelingforPiezoceramicActuator[J].OpticsandPrecisionEngineering, 2012, 20(1): 88-95.
[15]SmolaAJ,SchölkopfB.ATutorialonSupportVectorRegression[J].StatisticsandComputing, 2004, 14(3): 199-222.
[16] 韩彦彬, 白广忱, 李晓颖,等.基于支持向量机柔性机构动态可靠性分析[J].机械工程学报,2014,50(11):86-92.HanYanbin,BaiGuangchen,LiXiaoying,etal.DynamicReliabilityAnalysisofFlexibleMechanismBasedonSupportVectorMachine[J].JournalofMechanicalEngineering, 2014, 50(11): 86-92.
(编辑 陈 勇)
Description of Nonlinear Characteristics of Piezoelectric Micro-manipulation Stage Based on SVM
Hu Junfeng Zheng Changhu Cai Jianyang
Jiangxi University of Science and Technology,Ganzhou,Jiangxi,341000
The nonlinear characteristics of micro-manipulation stage would be occurred due to the hysteresis of piezoelectric actuator, which might seriously affect the movement precision and repeated positioning accuracy of the stage. In order to solve the issue, a hybrid modeling method was proposed to describe the hysteresis characteristics based on Preisach and SVM. As for a one dimensional micro-manipulation stage, the sample points were chosen as the piezoelectric driving voltages and corresponding output displacements of the stage. The regression model of the hysteresis loop of the PEA was established by using SVM theory. The model might be used to predict the displacements corresponding to the voltages not at sample points. Combined with the Preisach model, the output displacement corresponding to any voltage sequence might be obtained. The experimental studies were carried out in order to verify the validity of the presented model. Arbitrarily selecting two sets of input voltage sequences, and the prediction value of the output displacements corresponding to the selected voltage sequences might be obtained by using the regression model and Preisach model. The measured values were obtained under the same voltage sequences by experimental tests. Comparing the measured values and predicted values, the results show that the relative error ranges of the two sets of the measured and predicted values are as 0.6%~2.1% and 0.02%~2.1%, respectively. Therefore, the predicted displacements are very close to the measured ones. It illustrates that the proposed model may accurately describe the nonlinear characteristics of the micro-manipulation stage in order to realize its precise movements.
micro-manipulation stage; piezoelectric actuator; Preisach model; support vector machine(SVM); nonlinear characteristics
2016-01-11
国家自然科学基金资助项目(51265016,51565016)
TH703;TP274
10.3969/j.issn.1004-132X.2016.22.006
胡俊峰,男,1978年生。江西理工大学机电工程学院副教授。主要研究方向为柔顺机构及智能控制。发表论文30余篇。郑昌虎,男,1991年生。江西理工大学机电工程学院硕士研究生。蔡建阳,男,1991年生。江西理工大学机电工程学院硕士研究生。

