响应面模型与混合优化算法相结合的锯片参数优化设计
田永军 段国林 夏晓光 张 萼
河北工业大学,天津,300130
响应面模型与混合优化算法相结合的锯片参数优化设计
田永军 段国林 夏晓光 张 萼
河北工业大学,天津,300130
针对传统算法在锯片声学特征优化中的局限性,提出了一种将二阶响应面模型与混合算法相结合的优化设计方法。在设计区域内应用D-optimal试验设计法抽取样本点,分别通过显式算法获取锯片声学、应力响应以及隐式算法获取锯片变形量,并用试验验证了数值模型的准确性,然后建立了由6个变量参数所决定的锯片的声学、应力以及刚度的二阶响应面模型;利用自适应模拟退火法和蛙跳混合算法对响应面模型进行循环逼近,获得了设计变量影响度以及最优结果。结果表明,在保证刚度和应力许可条件下,通过有限次数值分析,经全局优化后的最佳结构可降低空载噪声4~7 dB。数字算例表明,该方法适用于旋转类刀具的声学性能优化设计。
锯片;响应面模型;混合优化算法;动态;噪声
0 引言
锯机噪声按其工作状况分为切割噪声和空载噪声。切割噪声涉及诸多因素,如工件种类、切割参数等。空载噪声由空气动力学噪声和主轴噪声组成,其中空气动力学噪声是空载噪声的主要成分,是锯片旋转时周围空气流动诱发刀面产生振动形成的[1-2],并时常伴随“啸声”,据Bies[2]统计,锯切系统空载时间占用大部分工作时间(约80%),且空载噪声决定着锯机噪声的下限。随着绿色制造业的快速发展,噪声控制已成为刀具制造业的重要研究内容之一。因此,通过对锯片结构进行合理的优化设计,充分挖掘其设计潜力,是降低锯机噪声的有效途径。
针对锯片振动与噪声优化问题,诸多学者在理论和试验上展开了研究,Cheng等[3]将锯片基体结构设计为阶梯状,降低了空载噪声。Chen等[4]对锯片基体的槽孔等结构进行优化,获取了稳定性锯片。
国内外学者针对锯片结构设计这一研究热点提出了较多的方案[3-5],在降低锯机噪声、提高加工性能方面取得了显著效果。但这些研究方案给优化基体及锯齿结构提供的严密的数学分析和理论依据带来了一定的局限性。主要有两方面原因:一方面,边界条件大量简化。主要以静力载荷为边界条件,以结构受最大应力或变形为目标函数进行优化。但锯片高速旋转过程行为复杂,仅依靠静态方法难以准确描述力学、声学响应。另一方面,数值优化中采用启发式或梯度类算法。前者如蛙跳算法、遗传算法,是模拟自然进化过程一种全局寻优的算法;后者如共轭梯度法、梯度下降法,优化过程中要进行大量敏度运算和梯度分析。这些算法适用于静态结构的优化设计,而锯片旋转过程涉及复杂动态边界条件,其约束函数和目标函数难以显式表达,单独使用这些算法需反复进行数值计算,计算量大,难以得到最优解。启发式和梯度类相结合的混合式优化算法虽可加快求解进程,但计算量仍然巨大。
近年来,以响应面为代理模型的逼近类方法在结构的动态优化设计中逐渐得到了应用[6-9],其本质是采用逼近近似技术对已知离散样本点进行插值或拟合来实现对未知点响应的预测,用近似拟合数学模型来代替具有庞大自由度的有限元模型进行分析计算。Nguyen等[6]和Ren等[7]利用响应面方法分别对结构耐撞性以及散热风扇护罩的低噪音进行优化,取得了较好的结果。
本文基于响应面模型与混合优化算法相结合的方法建立了动态旋转锯片声学特征的优化设计模型。首先建立动态声学模型,考虑复杂的载荷激励以及声学边界条件,采用边界元/有限元耦合法对锯片的空载噪声声压级进行预估并用试验验证了仿真模型的准确性。然后,在D-optimal试验设计以及数值分析的基础上,采用二阶响应面法建立了以锯片空载噪声最小为目标函数,以满足刚度、应力许可为约束条件的代理函数,对其使用自适应模拟退火法和蛙跳算法的混合算法进行全局寻优,研究了锯片在空载条件下的结构参数对噪声的影响规律,并获取了最优锯片结构,提供了计算效率,降低了锯机噪声下限。
1 多场耦合分析及试验验证
可靠的数值结果是优化策略实施的基础。锯片声振耦合是结构振动与声学介质波动的相互作用而产生的声辐射问题。本文利用有限元(FEM)和边界元(BEM)耦合方法[8-9]对锯切系统空载噪声进行快速求解。FEM/BEM耦合法[8-9]原理是利用FEM求解旋转系统振动信息,将振动信息作为边界信息经BEM计算获取声场辐射信息。
1.1 锯片空载噪声辅射模型
锯机空载工作过程中,由电机驱动锯片作旋转运动,为了简化运动和实现对其工作过程噪声的预估,作以下假设:①锯片空转时主要噪声源为锯片振动,故将锯片及夹盘作为研究对象;②锯片周围空气流的马赫数较小(Ma<0.3),空气密度变化可以忽略不计,故认为气体不可压缩;③气体黏性系数为常数,忽略摩擦效应;④锯切系统的噪声辐射是在三维半空间中传播的,地面作为刚性面处理(法向振动速度为0)。
旋转系统模型如图1所示,参数如下:锯片直径a=350 mm,内孔直径b=25.4 mm,夹盘直径为120 mm。锯齿24个,锯片厚度为3 mm。边界条件如下:赋予锯片及夹盘结构绕Z方向的转动自由度,速度为2800 r/min,约束其他方向自由度。声学边界中半空间问题处理方法如下:使用*DEFINE_PLAN关键字将距离旋转结构底部1 m的X-Z面作为刚性体反射面。

图1 锯片动态旋转系统仿真模型
1.2 数值分析及结果
本文采用实体单元对锯片、夹盘进行离散,得到旋转系统振动响应的FEM模型,而BEM声学分析不能使用实体单元计算,必须使用二维壳单元,因此可利用LS_DYNA编写关键字*SET_SEGMENT(抽壳处理)在实体网格外表面生成二维单元组,即声学模型。此时BEM网格与FEM网格在对应位置节点坐标一致,从而保证了FEM计算得到的振动速度结果作为边界条件导入BEM声学边界时信息输入的完整性、准确性。
锯片结构的声辐射分析,需引入关键字*FREQUENCY_DOMAIN_ACOUSTIC_BEM_HALF_SPACE,该关键字用于提取锯片旋转系统在半空间环境下任意时刻振动信息,通过显式动力学方程并结合声振耦合方程[8-9]可得到锯片时域声辐射信息;对于锯片频域特征问题的处理,该关键字使用FFT技术将时域信号转换为频域信息,并利用汉明窗函数减少计算分析过程中的频谱能量泄漏及栅栏效应。
经多场耦合分析后将复杂激励下计算所得的速度响应由有限元计算模型映射到边界元模型中,可以获取外场域任意点辐射声压。为验证数值模拟准确性,通过试验(图2)从噪声与振动两方面进行对比分析。

1.锯片及振动监测点位置 2.激光测振仪OFV505 3.麦克(距离锯机1 m)及声学分析工具LMS Test.lab图2 噪声与振动试验设备
对比图3发现数值计算声压级水平在稳定阶段与试验数据基本吻合,两者相差15%之内,模拟值略低的原因是尚未考虑主轴噪声等外界环境。在启动阶段由于锯机结构间复杂耦合关系以及外界环境影响,出现“啸声”现象,仿真中模拟该特征比较困难。

图3 锯片旋转过程声学特性曲线
锯片的横向振动速度直接决定了噪声大小以及锯片在旋转过程中的稳定性。图4中提取了在稳定阶段锯片外半径0.8R处的横向振动速度,计算结果和试验结果接近。由此证明耦合模型具备较高的可靠性,因此,数值模型可以保障响应面模型构造精度。

图4 锯片表面横向振动速度曲线
2 响应面模型与优化算法
响应面模型和混合优化算法结合的锯片参数优化设计法分为三部分:①利用试验设计理论分布一定数量的锯片样本点并对其进行数值计算,得到响应值;②再通过这些响应值构造目标或约束函数的近似多项式响应面数学模型;③采用混合优化法对响应面模型循环逼近优化得到最优解。其中前两部分为响应面模型的主体,响应面法是一种近似代理模型技术,通过构建显式的近似数学模型替换原设计方法中隐式问题。
2.1 D-optimal试验设计理论
本文采用D-optimal设计方法[10]进行试验样点的选取,其思想是选取的试验点可使模型的渐进协方差矩阵的行列式最小,从而得到更可靠的参数估计。
2.2 多项式响应面模型拟合
本方案利用二阶多项式方法构建响应曲面,数学模型如下[11]:
(1)
式中,xj为设计变量;β为模型回归系数。
式(1)中,回归系数个数N=(n+2)(n+1)/2,为了保证未知回归系数求解的准确性,通常要求设计样本点xi(i=1,2,…,M)个数M要大于回归系数个数[11]。本文取样本点个数为
M=1.5N+1
(2)
2.3 混合优化算法
自适应模拟退火(adaptive simulated annealing,ASA)算法[12]是基于Monte-Carlo迭代求解策略的一种用于解决具有多峰和非光滑性的高难度非线性优化问题的全局最优的随机搜索算法。其本质是模拟固体退火的机理建立起的启发式算法[11-12],通过控制温度的变化过程来实现大范围的粗略搜索与局部的精细搜索,收敛速度较快。这种算法的最大困难在于难以满足准确的收敛标准,通常解决方案是增加计算时间,以寻求全局最优解,这无疑增大了计算量。
混合优化算法是一种通过全局优化算法与基于局部梯度优化算法相结合的方法,该算法兼备两者优点[11],既能在响应面模型优化过程中增大全局寻优速度又易于实现。本文采用的混合优化算法是ASA与蛙跳算法,核心思想如下:利用ASA法的Metropolis判断准则以动态的概率寻求一个较好的初始点,然后采用蛙跳算法进行局部挖掘,不仅扩大了搜索时的寻优范围而且加速了优化进程。
3 结构声学性能优化流程
响应面模型和混合优化法相结合的设计法,使得原有计算复杂的、具有大自由度的锯片声学分析模型被简单有效的多项式代理模型代替,优化算法可直接对近似解析模型式(1)循环逼近获取最小目标函数值。
图5为锯片声学性能优化体系流程图,步骤如下:
(1)定义变量、目标函数以及约束函数。
(2)根据D-optimal试验设计方案,分别在锯片静力刚度响应模型和动态声学响应模型的设计空间内选取样本点。
(3)通过参数建模方式,依据步骤(2)的离散的试验样点数据构建静力网格模型和动态声学网格模型。
(4)使用Newmark法和显式动力学法对样本点进行计算,分别获取静力刚度响应模型和动态声学、力学响应模型的响应值。
(5)分别对步骤(4)的响应值进行二阶多项式响应面模型初次拟合,并建立目标函数(锯片噪声声压级)、约束条件函数(锯片轴向位移、锯片等效应力)响应面模型。
(6)利用混合优化算法对步骤(5)对应的响应面模型进行一次优化,并根据拟合精度准则,判断响应面是否满足精度要求,若不满足则继续循环。

图5 优化体系流程图
(7)根据整个优化体系的收敛标准对相邻二次优化中的设计变量、目标/约束函数响应值进行收敛判断。收敛准则为
|(x(k)-x(k-1))|/‖d‖=εx
(3)
|(f(k)-f(k-1))/f(k-1)|=εf
(4)
其中,x为设计参量;d为设计域长度;收敛公差εx=0.01;f为目标函数;k为迭代次数;目标函数公差εf=0.01。若满足收敛则获得最优解。
(8)若不满足优化体系收敛标准,主要原因是响应曲面局部精度不足,最优解附近的试验点较少,无法准确表达设计域真实响应,此时需对响应面模型进行修正,即通过调整设计区间,以最佳设计点作为拟合中心重新构建高精度近似模型。本文采取序列响应面方法[13]对近似模型的回归过程进行重构,其思想如下:将设计域离散为一系列子兴趣域或子信赖域,在各个子区间对响应曲面进行近似优化,优化过程中,每一个子信赖空间生成原响应面模型的一个当前近似最优设计点,新的子信赖空间以当前的最优设计点作为信赖域的中心,并通过移动、缩放等方式在设计域中连续更新,直到寻找到最佳点。如图6所示。

(a)移动 (b)缩放 (c)移动与缩放图6 兴趣域更新方案
子信赖域更新是以第k次子信赖域的优化设计点作为第k+1次子信赖域的中心,新信赖域中第i个变量的变化范围与收缩率λi有关,其数学关系如下[11,13]:
(5)
(6)
利用序列响应面方法不断缩减设计空间以提高代理模型的拟合精度,通过多次对上述步骤循环,结合混合优化算法不断搜索直至满足步骤(7)函数的收敛准则。
4 声学特征优化问题
本优化体系不考虑锯片开槽结构、材料对噪声的影响,旨在针对某一普通类型锯片的基本结构进行优化并穷尽其设计的可能。
4.1 参数化模型
结构的参数化表示是优化体系的设计基础,这一关键步骤决定了设计变量的数量。高速旋转过程中由于锯齿结构作用导致空气流动复杂[1-2],空气流经锯齿产生瞬变的分离流和涡流,这种分离流不断依附于锯片表面不仅产生明显的压力梯度,同时迫使锯片持续振动,从而激发噪声辅射,而锯片外表面夹盘的大小对锯片整个结构的横向振动响应亦有明显影响。
针对上述描述,在优化直径为350 mm这一类型锯片的过程中将锯齿结构、夹盘尺寸作为设计变量(图7):夹盘直径为x1,水槽深度、直径分别为x2、x3,锯齿间半夹角为x4,锯齿数量为x5,锯片厚度为x6。通过6个变量进行参数化建模即可确定完整锯片结构。

图7 锯片结构设计变量示意图
4.2 优化数学模型
优化过程中,既要充分挖掘低噪声锯片的设计潜能,又要确保结构安全性能,而往往优化设计中噪声的最小化和安全性是一对矛盾,如何协调这一矛盾至关重要。
4.2.1 约束条件
锯片优化发展趋势是减小锯片厚度,而过小的厚度会直接降低锯片横向刚度以至锯片偏摆过大。同时,旋转过程中锯片的等效应力也不能超过许用应力。因此,优化的约束条件如下:①锯片的最大静态挠度(刚度),挠度具体测量方式见文献[14];②旋转过程中结构的最大等效应力。具体表示如下:
(7)
式中,Dmax为静载荷条件下锯片最大挠度;σemax为最大等效应力。
4.2.2 目标函数
式(7)中设计变量描述见表1。以锯片高速旋转过程声学噪声有效值的最小值为目标函数,数学表达式如下:
min f(X)=f(x1,x2,…,x6)
(8)
4.3 响应面模型拟合及变量影响度
锯片声学特征进行优化时,选择6个设计变量,经D-optimal试验设计法并由式(2)确定每次

表1 设计变量
迭代的样本点数为43。将样本确定后,分别利用静态、动态模拟计算出各试验样本点的响应值,并经序列响应法通过不断调整设计域循环逼近获取近似响应面函数。
通过对基函数以及交叉基函项进行拟合。目标函数与设计变量关系式如下:
f(X)=2.58×109-4.2×1010x1+3.07×109x2-
3.79×109x3-9.11×105x4+5.60×105x5-
1.10×109x6-3.42×1010x1x2+2.21×1010x1x3+
5.53×106x1x4-3.64×106x1x5+2.19×1010x1x6+
5.69×109x2x3+9.17×106x2x4+1.05×105x2x5-
1.99×1010x2x6+4.29×106x3x4-1.12×107x3x5+
5.84×109x3x6-50.4x4x5+1.61×106x4x6+
(9)

表2 响应面模型精度检验
根据数据统计分析可得出自变量与各响应之间的贡献程度。由图8a可知,锯片水槽倾斜角度与噪声声压级水平负相关,即增大倾斜角度有利于降低噪声;在一定程度上随着锯齿个数增大,噪声会增大;一定范围内夹盘的半径增大有利于降低噪声,其主要原因是增大夹径比导致系统整体刚度增大从而减少振动[15]。由图8b可知,对锯片挠度影响最大的为锯片厚度。由图8c可知,水槽倾斜角以及结构厚度都对锯片等效应力有明显的影响。

(a)声压级水平
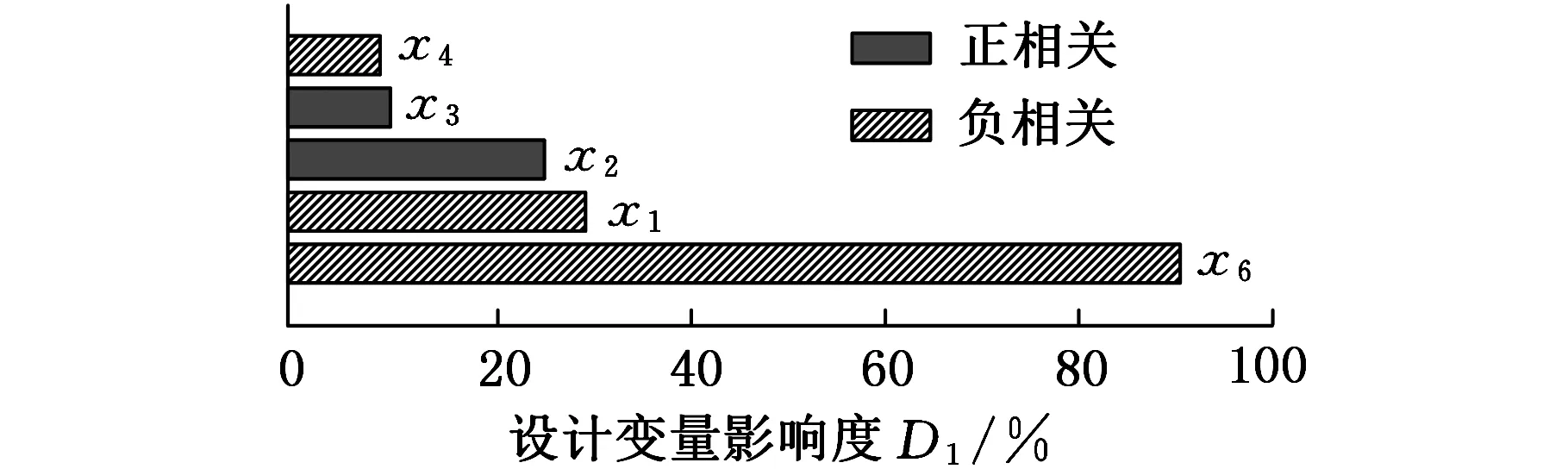
(b)锯片挠度

(c)锯片最大等效应力图8 设计变量对输出响应的影响水平
4.4 结果分析
通过模拟退火法和蛙跳法对满足精度要求的响应面模型在约束条件下的可行域内不断寻优即可获取最佳值。为直观表达拟合函数与设计变量关系,以目标函数随设计变量x4、x5变化(图9)为例进行分析,图9可反映最佳的寻优区间和非可行区间,通过在此类可行域进行搜索最终可获取满足刚度和应力条件的低噪声锯片。

1.可行域 2.限制域 3.非可行域图9 试验样本点声压级等高线二维图
经6次迭代逼近,得到设计变量的最终优化结果(表3),其中齿数x5取整数值。优化前后的声压水平时域曲线如图10所示。由于锯片发展趋势之一是减小厚度,而厚度增加可以减小锯片变形量,保持结构稳定,此时若将优化后锯片厚度减小到0.28 mm,锯片挠度为0.523 mm,虽超出约束条件,噪声略有增加,但仍控制在5%范围内。因此,通过本优化体系分析设计变量对锯片性能的影响规律,不仅可以在全局优化过程中减少试验次数、降低试验成本,而且可提高低噪声锯片的正向开发能力。

表3 第6迭次中部分样本变量与优化结果

图10 优化前后锯片空载噪声声压级曲线
5 结论
(1)利用参数化建模方式,结合D-optimal采样技术及二阶多项式函数构建了基于近似模型管理的锯片旋转系统声学优化设计体系,该优化方法代替传统算法中使用启发式算法或梯度算法中计算量庞大的目标特性计算模型,不仅减少了试验次数,降低了试验成本,而且在刀具声学优化领域具有实际意义。
(2)通过对设计变量影响度的分析,得到设计变量对锯片的声学、变形以及应力等性能的影响规律,这对于高性能锯片正向研发能力的提高具有指导意义。
(3)基于优化设计体系将直径为350 mm的普通锯片的空载噪声降低了4~7 dB,该方案同样适用于旋转刀具或类似复杂机械结构的优化设计。
[1] Leu M C,Mote C D.Origin of Idling Noise in Circular Saws and Its Suppression[J].Wood Science and Technology,1984,18(1):33-49.
[2] Bies D A.Circular Saw Aerodynamic Noise[J]. Journal of Sound and Vibration,1992,154(3):495-513.
[3] Cheng W,Yokochi H,Kimura S.Aerodynamic Sound and Self Excited Vibration of Circular Saw with Step Thickness I:Comparison of Dynamic Characteristics between the Common Circular Saw and the Circular Saw with Step Thickness[J].Journal of Wood Science,1998,44(3):177-185.
[4] Chen K N,Chang C,Huang J C.Optimum Design of Diamond Saw Blades Based on Experimentally Verified Finite Element Models[J].Computer-Aided Design and Applications,2012,9(4): 571-583.
[5] 吴军涛.组合结构金刚石圆锯片锯切性能及结构优化设计研究[D]. 济南:山东大学,2007.
[6] Nguyen P T L,Lee J Y,Yim H J,et al.Optimal Design of Vehicle Structure for Improving Small Overlap Rating[J].International Journal of Automotive Technology,2015,16(6):959-965.
[7] Ren G, Heo S, Kim T H,et al.Response Surface Method-based Optimization of the Shroud of an Axial Cooling Fan for High Performance and Low Noise[J]. Journal of Mechanical Science and Technology,2013, 27(1):33-42.
[8] Dos Santos N,Gerbeau J F,Bourgat J F.Partitioned FSI Strategy for Simulations of a Thin Elastic Valve[C]//ECCOMAS CFD Proceedings.Delft,2006:3147-3170.
[9] 王峥,洪明,刘城.基于FEM/BEM的浸水结构振动及声辐射特性国内研究综述[J].船舶力学,2014(11):1397-1414. Wang Zheng,Hong Ming, Liu Cheng.Domestic Review of the Submerged Structure Vibration and Acoustic Radiation Characteristics Based on FEM/BEM[J].Journal of Ship Mechanics,2014(11):1397-1414.
[10] de Aguiar P F,Bourguignon B,Khots M S,et al. D-optimal Designs[J].Chemometrics and Intelligent Laboratory Systems, 1995, 30(2): 199-210.
[11] Stander N,Roux W,Eggleston T,et al.A Design Optimization and Probabilistic Analysis Tool for the Engineering Analyst[M].Livermore:LSTC,2007.
[12] 王春燕,赵万忠,赵婷.电动轮汽车差速助力转向系统路感优化[J].中国机械工程,2012,23(1):122-125. Wang Chunyan, Zhao Wanzhong, Zhao Ting. Road Feel Optimization of Differential Steering of Electric Vehicle with Motorized Wheels[J].China Mechanical Engneering,2012,23(1):122-125.
[13] Stander N,Craig K J.On the Robustness of a Simple Domain Reduction Scheme for Simulation-based Optimization[J].Engineering Computations,2002,19(4): 431-450.
[14] Karpovich S S,Latushkina S D,Karpovich S I,et al.Static Stiffness of Circular Saw Blades[C]//Proceedingsof BSTU,Wood and Woodworking Industry.Minsk,2012:170-173.
[15] 肖杰.圆盘锯锯切噪声控制的研究[D].武汉:华中科技大学, 2004.
(编辑 陈 勇)
Optimization Design of Low Noise Circular Saw Parameters Combining Response Surface Model with Hybrid Optimization Algorithm
Tian Yongjun Duan Guolin Xia Xiaoguang Zhang E
Hebei University of Technology,Tianjin,300130
Focusing on inherent limitations in the traditional optimization methods for structure parameters of low noise circular saw, an optimization combining response surface model with hybrid algorithm was proposed to optimize the design of dynamic rotating blades. Firstly, a set of experimental design data points were extracted by D-optimal experimental design scheme,then the points were calculated respectively by display algorithm for acoustic, stress response and implicit algorithm for deformation saw blades.Then the corresponding response surface models were set up by the points’ responses. Finally, these second-order regression models were optimized by adaptive simulated annealing and leapfrog algorithm. The results show that under the conditions of safety, by a limited number of value analysis after the optimization, the final structure may reduce the idle noise 4~7 dB.Numerical example indicates that this method is suitable for the optimization design of acoustic properties of rotating cutting tools.
circular saw; response surface model; hybrid optimization algorithm; dynamic; noise
2016-01-19
天津市自然科学基金重点资助项目(11JCZDJC23100);河北省自然科学基金资助项目(F2014202241)
TH122;TB53
10.3969/j.issn.1004-132X.2016.22.008
田永军,男,1988年生。河北工业大学机械工程学院博士研究生。研究方向为动力学优化设计、机械振动与噪声控制。段国林,男,1963年生。河北工业大学机械工程学院教授、博士研究生导师。夏晓光,男,1988年生。河北工业大学机械工程学院博士研究生。张 萼,女,1989年生。河北工业大学机械工程学院硕士研究生。

