基于等效运动副化及运动副退化的公差分析法
尹立明 叶佩青 张 辉
清华大学精密超精密制造装备与控制北京市重点实验室,北京,100084
基于等效运动副化及运动副退化的公差分析法
尹立明 叶佩青 张 辉
清华大学精密超精密制造装备与控制北京市重点实验室,北京,100084
针对公差不仅在数值上具有随机性,其所约束的几何特征在空间的位置姿态上也具有随机性的特点,提出了公差约束等效运动副化及运动副退化法。等效运动副化将公差约束的几何特征转化为被运动副控制的几何特征,该等效运动副本身是虚拟的具有多自由度的等效运动副,将公差约束的几何特征转化为被多自由度运动副控制的几何特征,装配体转变为一个无误差的开环机械臂,考虑到因装配工艺而产生的不同运动副自由度之间的相互制约的现象,采用运动副退化法去除冗余自由度,由此建立装配体公差分析模型,并将装配体公差模型分析的数值与加工装配体的实验检测值进行对比。
公差分析; 等效运动副化; 运动副退化; 公差累积
0 引言
特征要素形位精度不仅受到零件本身尺寸公差与形位公差的影响,也受到参与到装配顺序、装配环节[1]中各个零件的尺寸公差与形位公差的影响。现有公差研究与公差分析主要解决两个方面的问题,即零件层面的公差语义表述[2-3]、几何表述和装配层面的公差累积与影响[4-5]。特征要素所处空间位置姿态形态复杂,且具有随机性[6],公差设计的目的就是给出满足产品功能要求的尺寸与形位误差的可行域空间[7],将特征要素刚体化[8-10]是目前公差研究中被广泛接受的处理方法,那么特征要素公差范围就转变为实际特征要素对理想几何体的形位偏离,这样处理便于采用数学工具[11-12]进行分析计算,小位移旋量(small displacement torsor, SDT)理论建立了标准几何体公差的数学模型[8],用于分析零件特征要素公差是否满足设计公差要求的层面,和讨论零件特征要素数学模型是否符合如最大实体要求、最小实体要求等原则作用的范围,难以应用于解决设计环节、自顶向下设计流程中的根本问题[13]。进行基于装配顺序的部件公差分析是以装配体各零部件之间装配顺序为基础,通过图表法建立定位面之间公差传递关系[14],进而建立线性尺寸链[15]或包含函数数值关系[16]的尺寸链求解模型进行求解,但无法体现公差不仅在数值上具有随机性,而且在所约束的几何特征在空间的位置姿态上更具有随机性的特点。被加工零件特征要素的随机性体现在数值的随机性与位置姿态的随机性这两个方面,公差分析中采用最大数值求解、均方根、Monte Carlo方法[17-19]处理零部件在数值上的随机性的特点是满足要求的,但这不能体现特征要素在尺寸公差与形位公差共同约束下具有的位置姿态的随机性问题,特别是对于装配体公差分析而言这一点尤其重要。对于装配体公差分析,存在两个需要解决的问题:①位于装配体中的特征要素的位置姿态公差模型的建立;②可以表达任一位置姿态的公差数学模型的建立。对于问题①,有研究采用坐标变换法解决公差偏离的问题,采用空间运动学求解某个特例的装配体公差分析问题,但并没有讨论公差约束之间的相互作用关系。因此,本文提出了基于公差约束等效运动副化及等效运动副退化的方法,建立了基于SDT理论的装配公差分析模型。对于问题②,本文讨论并给出了可以表达基于6个自由度的任一位置姿态的公差数学模型,从而避免了公差分析中不失一般性的假设,数学表达式的建立也为计算机编程和分析计算提供了算法程序。
1 结构设计与公差约束
根据功能要求设计结构并根据经验初步给出公差要求,该装配体结构共由3个零件组成,零件结构、尺寸要求如图1~图3所示,公差要求见表1~表3,装配体结构如图4所示,零件结构设计中影响到孔相对于机架定位面的公差见表4。

(a)主视图(b)剖视图图1 结构1公差及尺寸要求

(a)主视图(b)剖视图图2 结构2公差及尺寸要求
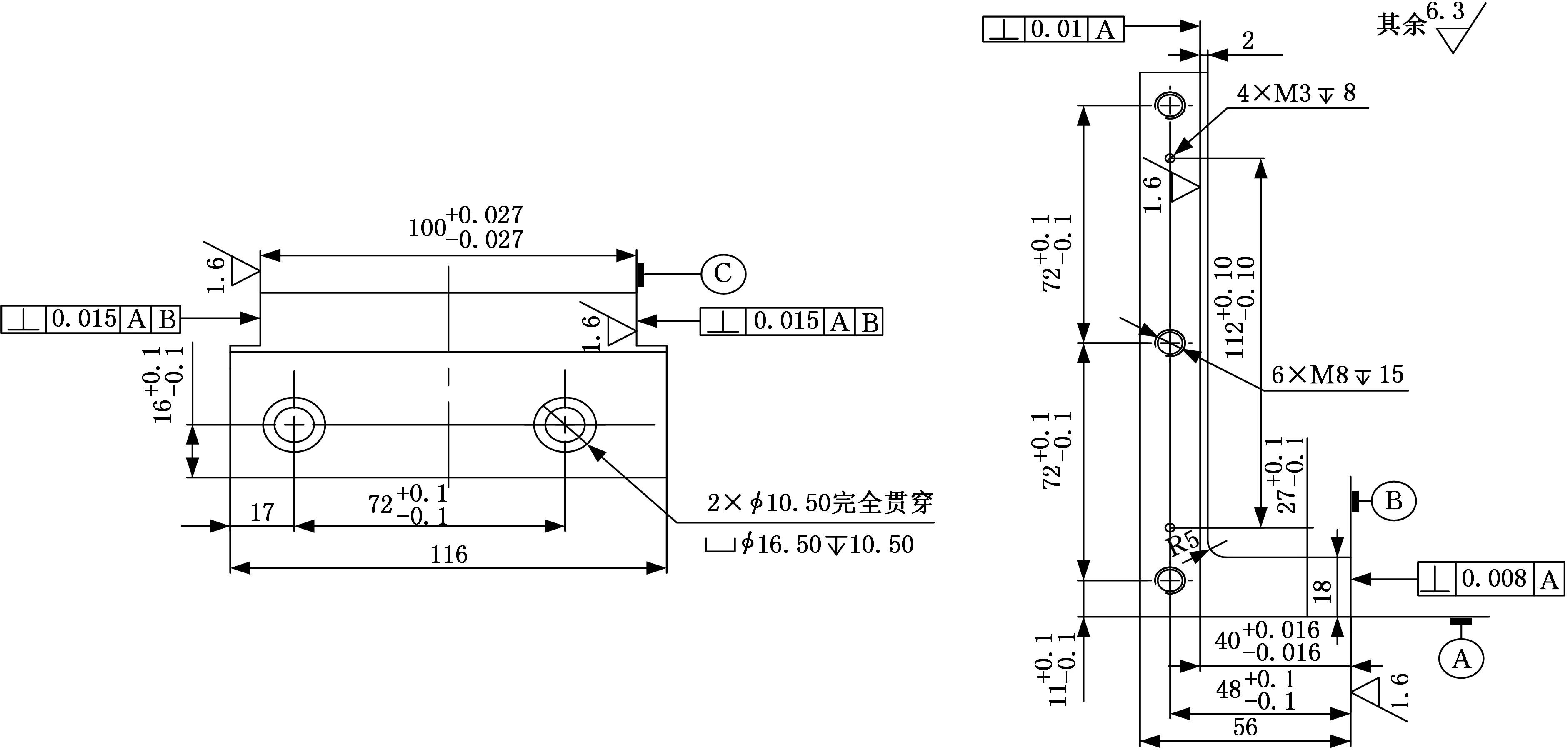
(a)底向约束示意图(b)侧向约束示意图图3 结构3公差及尺寸要求

序号特征/基准公差类型公差值(mm)1面/面0.0062面/面0.0153面/面0.0064面/面0.0155面/面0.0066轴/面0.0067轴/面0.0108孔0.2179面/面0.015

表2 结构2公差类型及公差值

表3 结构3公差类型及公差值

图4 装配体结构图
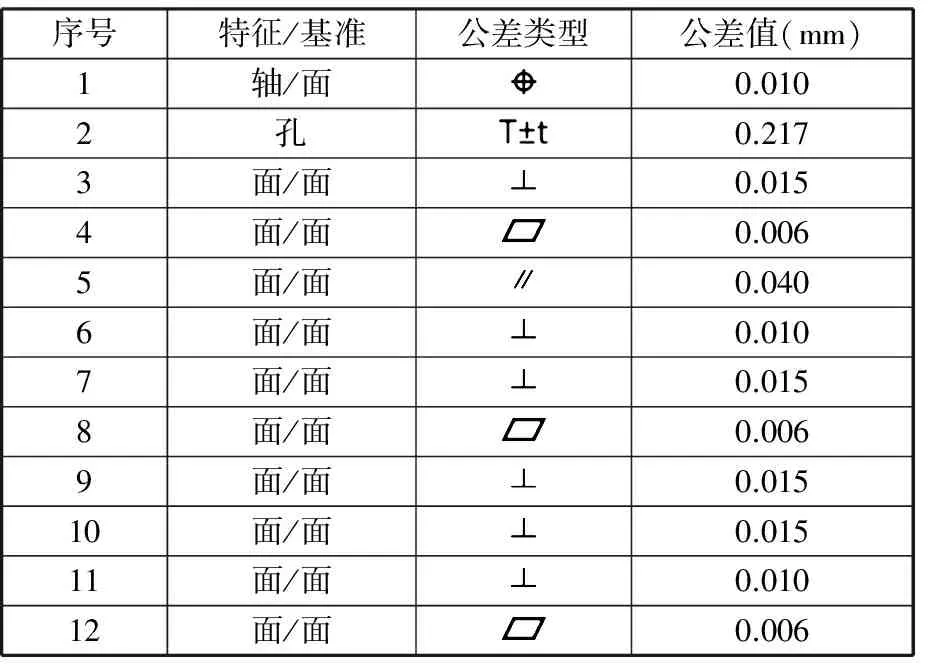
序号特征/基准公差类型公差值(mm)1轴/面0.0102孔0.2173面/面0.0154面/面0.0065面/面0.0406面/面0.0107面/面0.0158面/面0.0069面/面0.01510面/面0.01511面/面0.01012面/面0.006
2 等效运动副化
对上述公差约束下的装配体组装件进行等效运动副变换,从装配流程上分析,装配体安装后影响锥顶位置精度的公差共12个,因此,对装配体运动副变换后的构件如图5所示,图5a是装配体安装示意图,图5b为等效运动副的刚体结构,图5b中①,②,…分别表示第1、第2、第3个运动副,其中数字的顺序表示运动副计算流程的顺序,这里的运动副均为具有多个自由度的复合运动副,因此图示的形状并不代表运动副的形式。
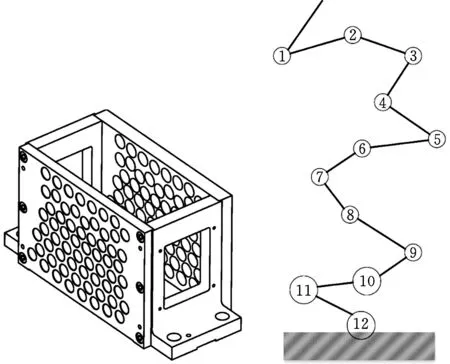
(a)装配体实际结构 (b)等效运动副转化体图5 装配体的公差约束的等效变换
3 公差数学模型的建立
加工特征相对于理想特征产生的偏离可以用偏离矩阵Rot(x,θ)、Rot(y,θ)、Rot(z,θ), τxyz(x,y,z)表示,根据刚体运动学知识,空间刚体产生运动可以分解为绕x、y、z轴的3个转动自由度和沿x、y、z轴的3个移动自由度。绕轴x发生偏离,偏离角度为θx,则偏离矩阵表达式为
(1)
沿x、y、z轴发生偏离,偏离位移分别为δx、δy、δz,则偏离矩阵表达式为
(2)
绕y、z轴产生的转动偏离矩阵的表达式分别为
(3)
(4)
经过绕轴的转动偏离和沿轴都位移偏离,刚体的变换矩阵可以表示为
Tzyx=Rot(z,θ)×Rot(y,θ)×Rot(x,θ)×
τxyz(x,y,z)
(5)
在机构运动学中,式(5)中矩阵运算的次序是不可以更改的,因为不同次序最终将得到不同的刚体位置姿态,也就是运算次序的改变将使刚体运动发生差异,也因为加工误差是加工允许范围内的各种情况,是不能穷举的,因此,应用上述表达式对加工公差进行预测是不可取的。根据公差分析的需要,需要建立统一的公差表达式,统一表达式是公差分析环节的第一步。
泰勒级数展开式是化简复杂等式的有力工具,函数项sinθx和cosθy展开式分别为
(6)
(7)
采用泰勒级数展开后,绕x、y、z轴产生的转动误差偏离量Rot(x,θ)、Rot(y,θ)、Rot(z,θ)分别为
(8)
(9)
(10)
公差表达式为
(11)
A=δx-δy(θz-θxθy)+δz(θy+θxθz)
B=δxθz+δy(θxθyθz+1)-δz(θx-θyθz)
C=-δxθy+δyθx+δz
在精密机械中,公差相对于结构尺寸是极小值,公差偏离量θx、θy、θz、δx、δy、δz均为极小值,略去式(11)中二阶小量,式(11)将化简为
(12)
交换表达式中偏离矩阵的次序得到:
Tzyx=Txzy=Tzyx=Txyz=Tyxz=Tyzx
(13)
得到的式(12)与偏离矩阵的运算次序无关,因此,式(12)是可以用于公差分析的统一表达式。
设计人员给出的公差设计需要满足功能需求,ASME Y14.5-2005及GB/T1182-2008规定了几何特征与公差类型约束关系,表5给出了基于SDT理论的几何特征、公差类型、偏离向量相互对应的偏离向量。
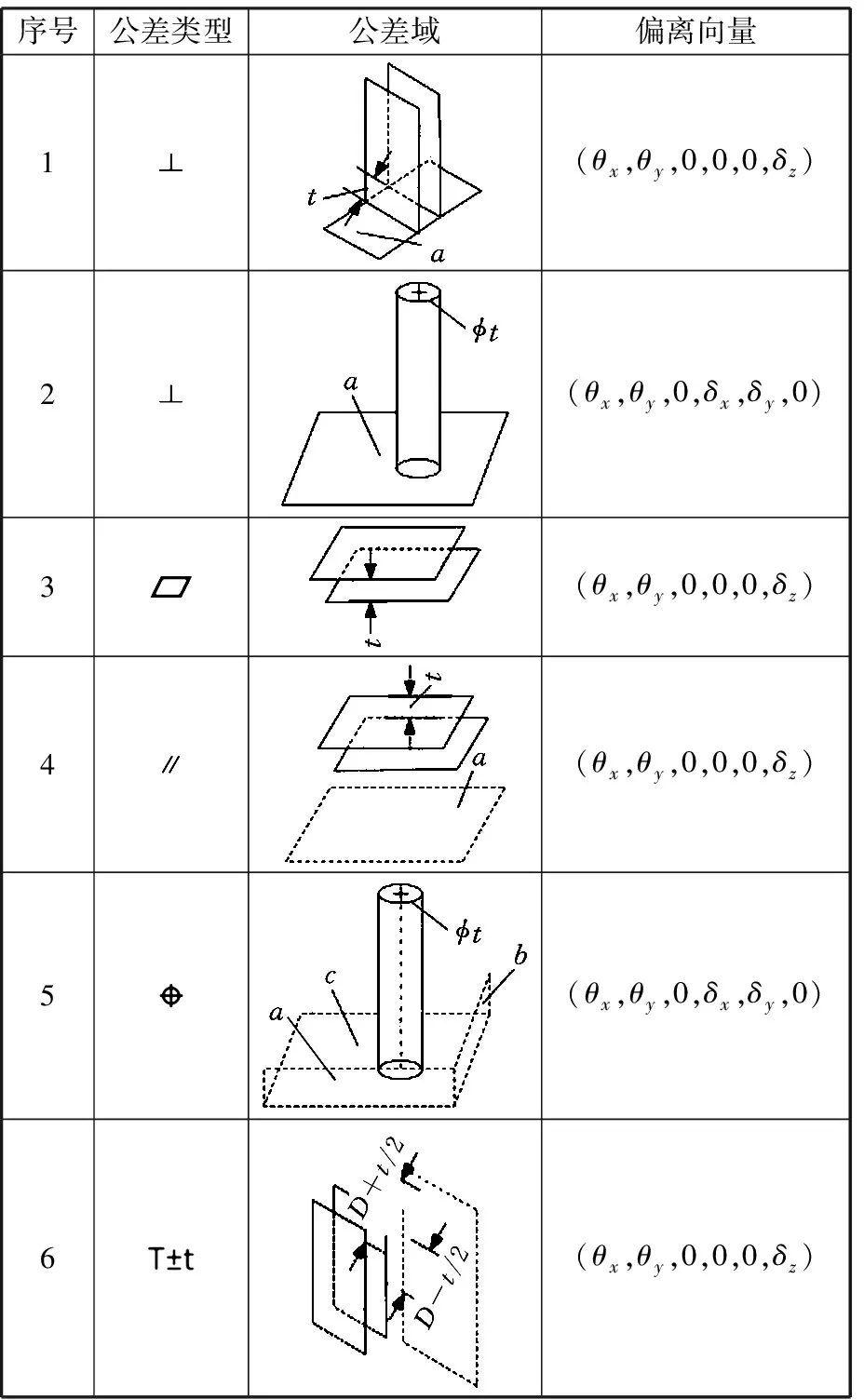
表5 公差类型与偏离向量
4 等效运动副自由度及运动副退化
装配体运动副的自由度需根据实际公差约束特征的形式确定,装配体公差约束特征的等效运动副自由度见表6,表6中运动副自由度根据约束类型、约束特征确定。

表6 等效运动副引入的自由度
装配过程中各定位特征所限定的自由度是存在差别的,因此,实际参与到装配中的运动副根据装配工艺及结构安装定位形式运动副将发生退化,退化后的运动副所引入的自由度将减少,根据装配工序、工艺分析,本装配体考虑运动副退化后的等效运动副自由度见表7。
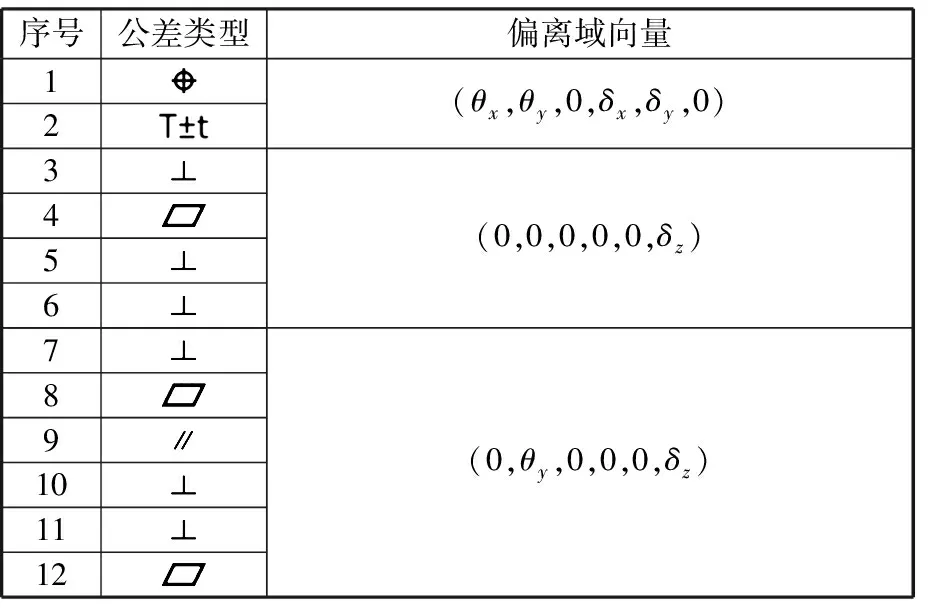
表7 等效运动副退化后的自由度
5 偏移向量坐标变换矩阵
为了便于分析每个特征的偏离量对装配体精度等的影响,需建立局部坐标系和全局坐标系,局部坐标系用于描述装配环中各个特征可能的偏离程度,全局坐标系用于描述结构体空间位置精度。全局坐标系建立在装配体底面理论几何中心上,局部坐标系建立在局部特征理论几何中心上,局部坐标系的z轴正向为特征的外法线方向,根据右手定则建立。局部坐标系下的偏离向量转换到全局坐标系下的偏离向量需经过方向矩阵变换,建立公差偏离向量的坐标转换矩阵,见表8,变换矩阵根据等效运动副的先后顺序建立。

表8 特征局部坐标相的方位转换矩阵
将局部坐标偏移向量转换到全局坐标系偏移向量的变换公式是
SDTG=d{i}×SDTL
(14)
其中,d{i}即变换矩阵,全局坐标系选择在装配体结构底面理论几何中心,采用笛卡儿坐标系;SDTG代表全局坐标系偏离向量,SDTL代表局部坐标系偏离向量。
6 装配体公差计算
基于加工特征数学模型的建立及处理后,便可以进行装配体公差分析,并进行相应的计算,结构位置精度变化的计算过程需从远离机架的一端开始,等效运动副转换后的运动传递链末端的运动副就是计算开始的运动副,并由末端向机架逐个进行分析和求解,即
(15)
(16)
(17)
其中,Di是第i个运动副在全局坐标系下的坐标位置。分析计算在MATLAB里编程实现,并输出计算结果,计算结果见表9。
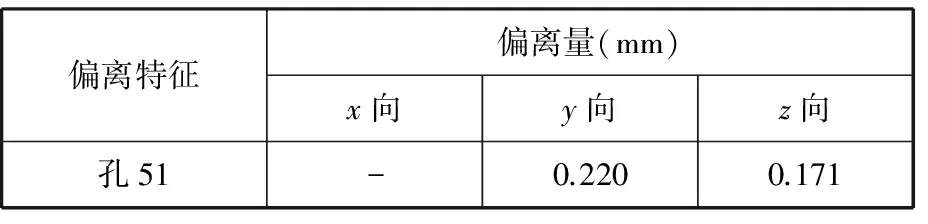
表9 特征偏离量数值计算值
7 实验
为了验证上述公差分析方法及程序的正确性,进行相关零件的设计、加工制造、装配、检测。零件的加工根据设计图纸进行,加工的零件经检测满足设计图纸要求,加工的零部件及检测如图6所示,装配环中的公差实验检测值见表10,实验采用蔡司三坐标测量机进行检测,三坐标测量机型号为ZEISS PRISMO navigator,线性尺寸E0检测误差为(0.5+L/500)μm,满足实验要求。对装配体进行实验检测,装配后孔51实验检测值见表11,实验结果表明,公差累积满足公差累积分析模型的预测结果。证明采用参数化、运动副化、程序化的公差累积分析模型是解决装配体公差累积分析的一种行之有效的方法。

图6 实验测试

序号公差类型偏离量(mm)10.0100620.2079330.0143840.0060750.0374960.0095170.0131680.0059790.01472100.01321110.09775120.00548

表11 装配体孔51实验检测值
8 结语
本文针对装配体公差分析问题,首先采用等效运动副化处理公差所引入的装配体结构位置姿态精度变化及采用运动副退化法处理不同运动副自由度之间的相互影响,然后给出了公差统一的数学表达式,最后将模型分析数值与加工装配体的实验检测值进行了对比,实验检测结果表明,基于等效运动副化及运动副退化的公差分析法是预测公差累积现象的一种行之有效的方法。后续开展的工作是将上述分析流程及分析方法程序化与可视化,通过图形的变动为设计人员提供直观的公差过程与结果。
[1] Wu Yuguang. Assembly Tolerance Analysis Method Based on the Real Machine Model with Three Datum Planes Location[J].Procedia CIRP,2015, 27: 47-52.
[2] Li H, Zhu H P, Li P G, et al. Tolerance Analysis of Mechanical Assemblies Based on Small Displacement Torsor and Deviation Propagation Theories[J].International Journal of Advanced Manufacturing Technology,2014, 72(1/4): 89-99.
[3] Li C L, Yang J X, Wang J Y, et al. A Comparison Study of Small Displacement Torsor and Analysis Line Methods for Functional Tolerance Analysis[J]. Advanced Materials Research, 2012, 605/607(4):358-364.
[4] Zhang W M, Chen C, Li Pengzhong, et al. Tolerance Modeling in Actual Working Condition Based on Jacobian-torsor Theory[J]. Computer Integrated Manufacturing Systems CIMS, 2011, 17(1):77-83.
[5] Hong Y S, Chang T C. A Comprehensive Review of Tolerancing Research[J]. International Journal of Production Research,2002, 40(11): 2425-2459.
[6] Chang-Hsin K, Jhy-Cherng T. An Analytical Computation Method for Statistical Tolerance Analysis of Assemblies with Truncated Normal Mean Shift[J]. International Journal of Production Research,2011, 49(7): 1937-1955.
[7] Barbero B R, Aragón A C, Pedrosa C M. Validation of a Tolerance Analysis Simulation Procedure in Assemblies[J]. International Journal of Advanced Manufacturing Technology,2015, 76(5/8):1-14.
[8] Li H, Zhu H, Li P, et al. Tolerance Analysis of Mechanical Assemblies Based on Small Displacement Torsor and Deviation Propagation Theories[J].International Journal of Advanced Manufacturing Technology, 2014, 72(1/4):89-99.
[9] Li X L, Li G H, Wang J Y, et al. Three Dimensional Assembly Tolerance Analysis of Gear Drivetrain[J]. Advanced Materials Research,2013, 655/657:1656-1661.
[10] 吴玉光,刘玉生.面向公差技术的几何要素自由度表示与操作及其应用[J].中国机械工程, 2015,26(11): 1509-1515. Wu Yuguang,Liu Yusheng. DOF Representation and Operation of Geometric Feature and Its Applications for Tolerance Technology[J].China Mechanical Engineering,2015,26(11): 1509-1515.
[11] Jaishankar L N, Davidson J K, Shah J J. Tolerance Analysis of Parallel Assemblies Using Tolerance-maps and A Functional Map Derived from Induced Deformations[C]//Proceedings of The ASME International Design Engineering Technical Conferences and Computers and Information in Engineering Conference.Portland, 2013:V03BT03A008.
[12] Govindarajalu J, Karuppan S, Manoharan T. Tolerance Design of Mechanical Assembly Using NSGA II and Finite Element Analysis[J]. Journal of Mechanical Science and Technology,2012, 26(10): 3261-3268.
[13] Sahani A K, Jain P K, Sharma S C. Tolerance Stack up Analysis for Angularity of Components and Their Assembly[J]. Procedia Engineering, 2014, 69(1):952-961.
[14] Marziale M, Polini W. Review of Variational Models for Tolerance Analysis of an Assembly[J]. Proceedings of the Institution of Mechanical Engineers Part B Journal of Engineering Manufacture, 2011, 225(B3):305-318.
[15] Dumas A, Gayton N, Dantan J Y, et al. A new System Formulation for the Tolerance Analysis of Overconstrained Mechanisms[J].Probabilistic Engineering Mechanics, 2015, 40:66-74.
[16] Tang S Y, Guan D, Wu X, et al. Analysis on Virtual Assembly Tolerance for Pitch-adjustable Lateral Propulsion Device [J]. Procedia CIRP, 2015, 27:131-136.
[17] 余治民,刘子建,董思科,等.基于蒙特卡罗模拟与响应面方法的公差建模[J].中国机械工程, 2015,26(4): 427-434. Yu Zhimin,Liu Zijian,Dong Sike,et al.Tolerance Modeling Based on Monte-Carlo Simulation and Response Surface Method[J].China Mechanical Engineering,2015,26(4): 427-434.
[18] Khodaygan S, Movahhedy M R.Tolerance Analysis of Assemblies with Asymmetric Tolerances by Unified Uncertainty-accumulation Model Based on Fuzzy Logic[J]. International Journal of Advanced Manufacturing Technology, 2011, 53(5/8): 777-788.
[19] Wang Hui,Yu Tianxiang,Pang Huan,et al. Mechanism Reliability Simulation Analysis for Multi-support Axis Seizure Considered Assembly Tolerance[C]//International Conference on Quality, Reliability,Risk,Maintenance,and Safety Engineering.Xi’an,2011: 35-41.
(编辑 陈 勇)
Tolerance Analysis Based on Equivalent Kinematic Pair and Degradation of Kinematic Pair
Yin Liming Ye Peiqing Zhang Hui
Beijing Key Lab of Precision Manufacturing Equipments of Tsinghua University,Beijing,100084
Subject to the random characteristics in deformations, position and value of the features which were constrained by tolerance, a method to analyze the stack-up of tolerance by deeming tolerance constrains to equivalent kinematic pair was proposed herein. Under the situation of equivalent kinematic pair, the features constrained by tolerance were transformed to the features constrained by n-DOF of kinematic pair and the assembly would be transformed to a robot arm, which connected by the rigid parts and without any errors. As the results of the assembly processes, the affections of interaction among different kinematic pairs were the emerging problems after transformed. To deal with that problems, the method of degradation for kinematic pair was proposed herein. Then the formula to analyze stack-up of tolerance was established based on the method of equivalent kinematic pair and degradation for kinematic pair. Finally, those methods were used to analyze a realistic assemble product, and compared the calculated values with the experimental results.
tolerance analysis; equivalent kinematic pair; degradation of kinematic pair; tolerance stack-up
2016-01-11
国家科技支撑计划资助项目(2015BAI03B002);北京市科技计划资助项目(Z141100000514015);清华大学自主科研项目(20111081026);清华大学摩擦学国家重点实验室自主研究课题重点项目(SKLT12A03)
TH115
10.3969/j.issn.1004-132X.2016.22.001
尹立明,男,1982 年生。清华大学机械工程学院硕士研究生。主要研究方向为结构优化与力学分析。叶佩青,男,1963年生。清华大学机械工程学院研究员、博士研究生导师。张 辉,女,1969年生。清华大学机械工程学院副研究员、博士研究生导师。

