磁致伸缩仪超声空化流的三维非定常数值模拟

夏冬生 孙昌国 于 彦 张会臣

大连海事大学，大连，116026



磁致伸缩仪超声空化流的三维非定常数值模拟

夏冬生 孙昌国 于 彦 张会臣

大连海事大学，大连，116026

采用Singhal完全空化模型和SSTk-ω湍流模型结合动网格技术对磁致伸缩仪超声空化流进行三维非定常数值模拟。计算结果表明，由于变幅杆高频振动，在靠近试样表面附近局部流场的压力和空泡体积组分变化具有周期性，压力波动的最低值可达到汽化压力，该局部流场可发生空化。由于空化，试样表面压力波动具有脉冲特征。压力和空泡体积组分在试样表面近似呈环形分布。在同一环形区域内，压力和空泡体积组分存在无规律断续脉动。试样表面中心区域空泡经历两次振荡后溃灭，产生强烈脉冲压力，最大脉冲压力可达约14 MPa。脉冲压力在试样表面按间隔环形区域分布，且随试样振动在相邻环形区域上交替出现。在磁致伸缩仪超声空化流场中，试件表面可近似多个声波发生源，各声波传播时相互叠加和干扰。在声波传播的过程中压力衰减很快，只是在距试样表面约20 mm内，压力有明显波动。

磁致伸缩仪；计算流体动力学；空化；脉冲压力

0 引言

空蚀是流体机械的一种主要破坏形式，严重影响流体机械的工作可靠性、工作效率和使用寿命。国内外学者对空蚀进行了广泛研究，其研究领域包括空蚀机理[1]、空化流场特征[2]、材料抗空蚀性能[3]及空化和空蚀影响因素[4]等。目前，研究者普遍接受的空蚀机制是微射流理论[5-6]和冲击波理论[7]。当空泡在固体表面附近发生溃灭时，产生高速微射流或(和)冲击波，其作用在固体表面形成显著的冲击压力。表面材料由于受到冲击压力的频繁作用而发生疲劳破坏。空化流流场特性和材料的抗空蚀能力决定了空蚀破坏是否发生及破坏的程度。

磁致伸缩仪是研究空蚀机理和测定材料抗空蚀性能的重要仪器之一。磁致伸缩仪的基本原理是利用具有趋磁性的传感器或压电传感器在交变电流作用下能够伸长或变短的特性，实现换能器端部在液体中高频振动，产生振荡型无主流空化。为了深入理解磁致伸缩仪空蚀实验中材料的空蚀行为及空蚀特征，研究振荡型空化流空化过程和空化流流场特征是十分必要的。Ahmed[4]利用磁致伸缩仪研究了温度对冲击压力、空化过程和金属铝空蚀行为的影响，发现空泡溃灭引起的冲击压力分布在试样表面圆形区域内，且与温度和径向距离密切相关：温度较低时，中心区域冲击压力最大；随温度升高，中心区域的冲击压力减小，易形成较多数量的空泡。Bai等[8]利用磁致伸缩仪和高速摄影技术对超声空化流流场中硬壁凹坑的驻气特性、微泡散逸特性以及空泡对空蚀坑发展过程的影响进行了研究。Burdin等[9]利用磁致伸缩仪和激光技术研究了超声空化的空泡体积含量、空泡大小分布以及超声功率的影响。由于空化的瞬时性、随机性和复杂性以及实验条件限制，磁致伸缩仪超声空化过程和流场特征的研究较缺乏。本文基于CFD方法，利用Fluent软件模拟磁致伸缩仪超声空化流流场，分析超声空化流场的压力、空泡分布等流场细节和空化发展过程，并根据空化流的流场特性来探讨磁致伸缩仪空蚀实验中试样的空蚀基本特征。

1 数学模型

1.1 空化流的控制方程

空化流一般由液体和含有蒸气、不可凝结气体的空泡群组成。本文采用基于均质平衡流理论的Singhal完全空化模型模拟超声空化流。该空化模型考虑了不可凝结气体的影响，将空化流视为由液体、蒸气和不可凝结气体三组元组成的气-液两相混合的单流体(即两相混合的均匀介质)。三组元共享同一物理场，如压力、速度等。假设空化过程为等温过程，忽略重力效应，则混合单流体的Favre平均的连续方程和动量方程分别为

(1)

(2)

其中，xi、xj、xk(i,j,k=1, 2, 3)为笛卡儿坐标，下标1、2和3分别代表x轴、y轴和z轴方向，ui是沿i方向的速度分量，p是压力，μ、μt分别为混合流体的动力黏度和湍流黏度，δij是克罗内克(Kronecker)数。

混合流体的密度ρm由下式计算：

(3)

其中，ρ是密度，f是质量分数，下标l、v和g分别代表液体、蒸气和不可凝结气体。

不可凝结气体一般选择空气并假设满足理想气体状态方程，其密度ρg由公式ρg=Wp/(RT)确定，其中，T为温度，通用气体常数R为8314.3 J/(kg·mol)·K，W为不可凝结气体的分子量。

空化过程中液-气相间的质量传输由蒸气质量分数fv的输运方程控制：

(4)

式中，Re、Rc分别为蒸发阶段(蒸气泡的产生和膨胀)和凝结阶段(蒸气泡的压缩和破裂)的源项，分别定义为蒸气的蒸发率和凝结率。

对于Singhal完全空化模型，Re和Rc从Rayleigh-Plesset方程推导得到，考虑了湍动能在空泡运动过程中的影响和不可凝结气体作为气核的影响等，其表达式如下[10]：

(5)

(6)

其中，σ为液体的表面张力系数；k为流场的当地湍动能；经验常数Ce=0.02，Cc=0.01。Singhal完全空化模型考虑了湍流压力脉动的影响，修正相变压力阀值pv从饱和蒸气压psat提高到pv=psat+pturb/2，其中，pturb为湍流引起的压力脉动，pturb=0.39ρmk。

1.2 剪切应力输运(SST)k-ω湍流模型

采用SSTk-ω湍流模型对以上控制方程封闭。SSTk-ω湍流模型是由k-ω模型和k-ε模型各乘以一混合函数相加而成的，其在近壁区等价于低雷诺数标准k-ω模型，在远离壁面区域等价于高雷诺数k-ε模型，而在混合区域由混合函数混合使用这两种模型[11]。SSTk-ω模型除了兼具以上两种模型在近壁区和远场计算的优点外，与k-ω模型相比，ω输运方程中还增加了交叉扩散项，同时在湍流黏度定义中考虑了湍流剪切应力的输运过程，从而使该模型适用范围更广。

SSTk-ω模型中湍动能k和比耗散率ω的输运方程分别为

(7)

(8)

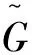
(9)

其中，S为平均应变率的张量模量，α、β*、β均为模型系数。湍流黏度μt按下式计算：

(10)

其中，对于高雷诺数，α*=1；对于低雷诺数，α*被修正，模型常数a1=0.31。

k和ω的湍流普朗特数Prk和Prω分别为

(11)

(12)

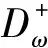
2 计算模型、网格划分和计算方法

2.1 计算模型和边界条件

图1所示为磁致伸缩仪空蚀实验装置，测试采用试样固定在变幅杆端面随变幅杆振动的方式。磁致伸缩仪的典型工作参数如下：变幅杆振动频率为20 kHz，峰-峰振幅为50～75 μm，功率为1 kW。忽略机电控制单元和冷却恒温装置，建立磁致伸缩仪空化流的计算模型，其模型尺寸如图2所示。变幅杆端部为直径20 mm的圆平面，浸入水深为20 mm。为了使声场近似为自由场，减少或避免声波的反射影响，将容器的直径和水深均设置为变幅杆直径的5倍。

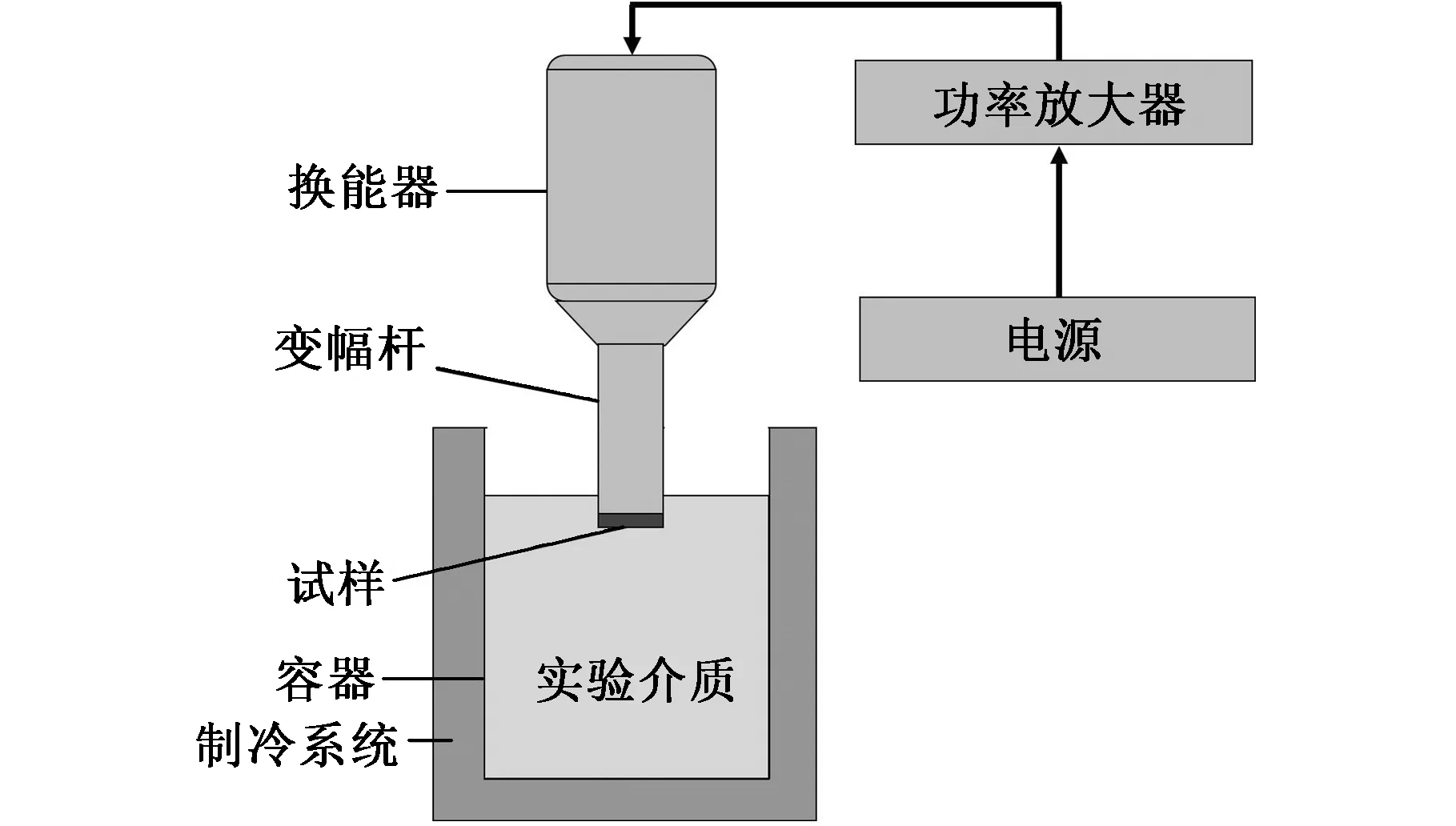
图1 磁致伸缩仪空蚀实验装置示意图

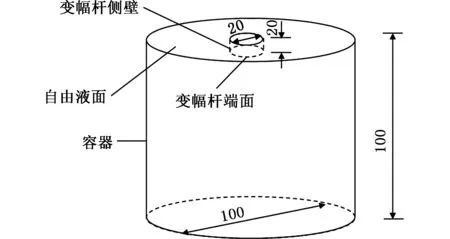
图2 三维计算模型

定义自由液面为压力进口，压力设定为101 kPa。所有壁面均采用无滑移边界条件。

利用动网格技术模拟变幅杆端面的振动，变幅杆端面的运动规律由用户自定义函数(user’s defined function，UDF)来描述。由于变幅杆端面运动为刚体平动，故调用DEFINE_CG_MOTION宏函数来编写UDF程序文件，需要指定变幅杆端面振动的速度。

根据变幅杆端面振动的运动规律，同时为有利于变幅杆振动模拟的实现，变幅杆端面的往复运动采用简谐运动近似表示，其位移方程为

z=Asin(2πft)

(13)

其中，z为振动位移；A为振幅；f为振动频率；t为时间。根据磁致伸缩仪的工作参数，计算时选取振动频率f为20 kHz，振幅A为30 μm。

将式(13)两边对时间求导，得到变幅杆端面的运动速度方程：

v=2πfAcos(2πft)

(14)

将编写好的UDF程序源文件调入Fluent中进行编译和连接，实现变幅杆端面按UDF文件所定义的方式运动。变幅杆端面的速度和加速度随时间变化曲线如图3所示。

2.2 网格划分

为提高数值模拟准确性和计算精度，对计算域采用六面体结构化网格划分，并对变幅杆端面和侧面附近网格进行加密处理。由于变幅杆振幅为30 μm，同时SSTk-ω模型要求壁面边界层网格的量纲一壁面距离y+在较低范围，则变幅杆端面边界层网格的首层高度设定为20 μm。但需要注意的是，由于变幅杆端面运动，其边界层网格发生畸变，将使变幅杆端面y+值发生显著变化，为解决这一问题，对所有网格类型采用弹簧近似光顺法来更新网格，并设置弹簧弹性系数为0，实现动边界附近的网格保持其原始形状和密度随动边界一起移动，网格变形在距动边界一定区域外进行。计算结果表明，变幅杆端面处第一层网格节点的y+值在0.7～9.0之间，满足SSTk-ω模型对y+的要求。流场计算域的网格划分如图4所示，整个计算域共得到约330万个网格。

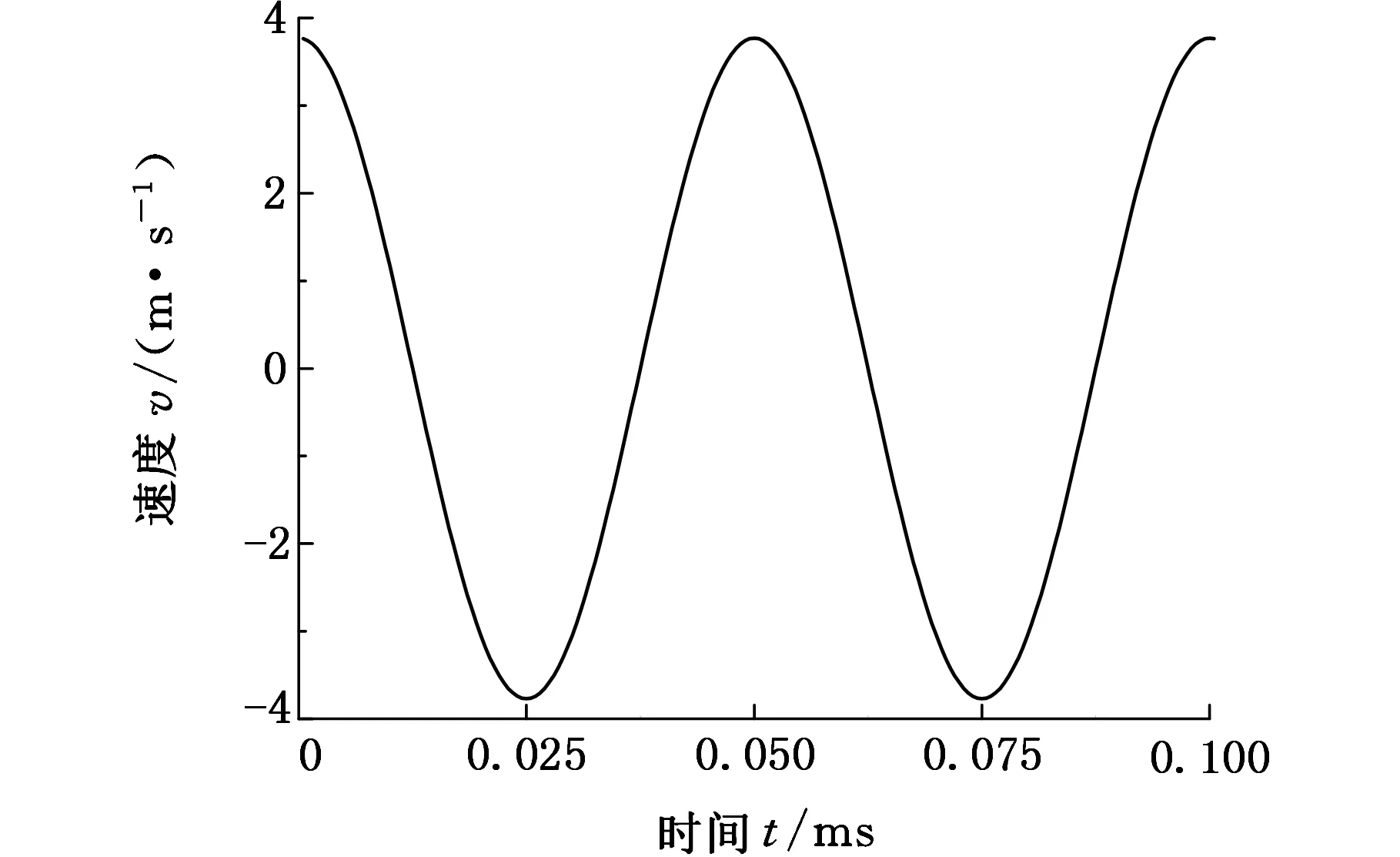
(a)振动速度变化曲线

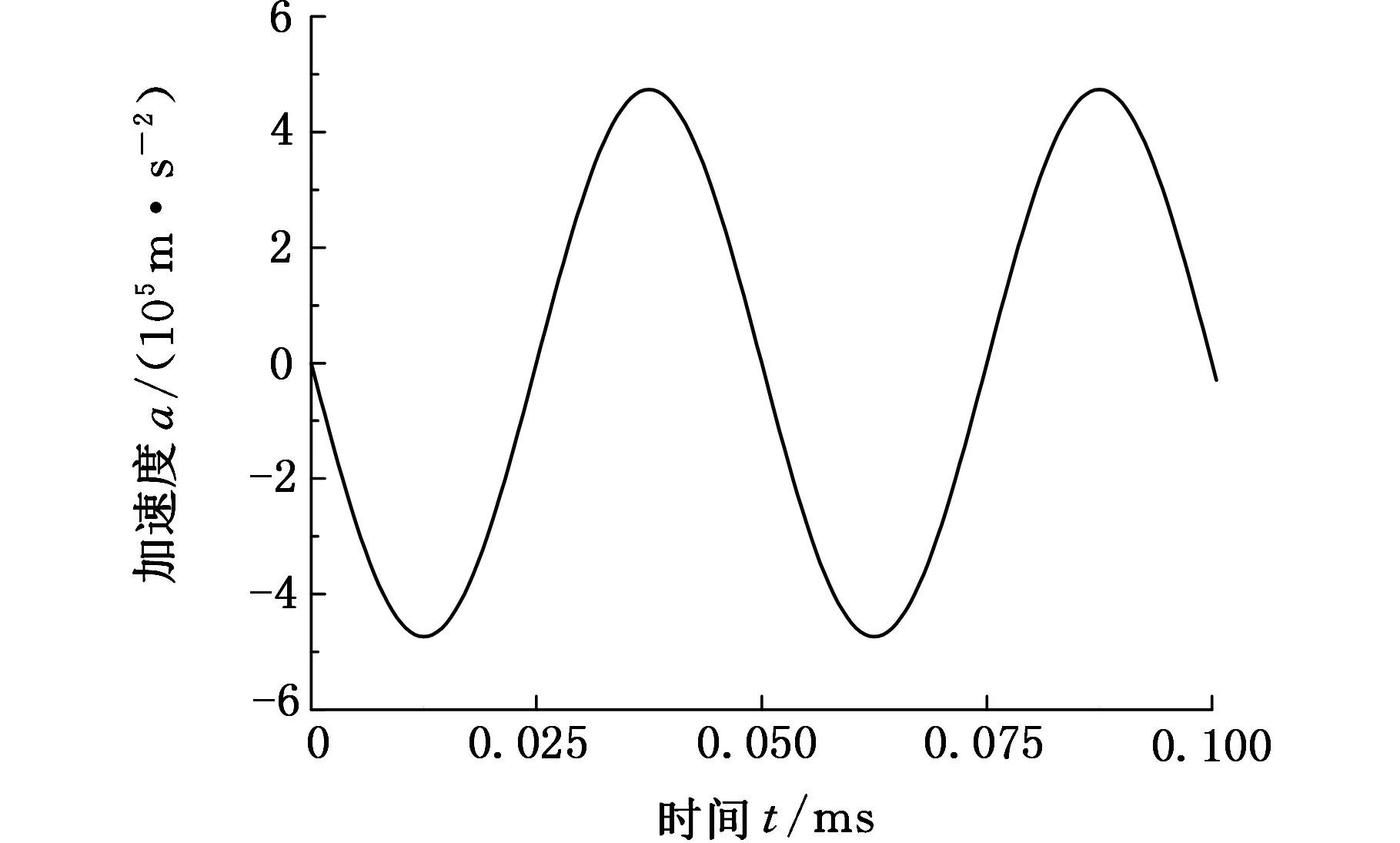
(b)振动加速度变化曲线图3 变幅杆端面的振动速度和加速度随时间变化曲线

(a)纵截面(b) 过试样表面的横截面图4 流场计算域网格

2.3 计算方法

采用有限体积法对控制方程组进行离散，对流项的离散采用二阶迎风格式，压力离散方式采用PRESTO!，扩散项的离散采用具有二阶精度的中心差分格式，时间离散采用一阶全隐式格式。为了提高非定常空化流计算的收敛速度和计算稳定性，先不考虑变幅杆振动进行定常计算，其收敛结果作为非定常计算的初始流场。定常和非定常计算分别采用SIMPLEC算法和PISO算法实现速度和压力之间的耦合求解。考虑到超声空化流场特性是瞬时变化的，为提高计算准确性和捕捉流场变化细节，本文将时间步长设定为变幅杆振动周期T的1%，即0.5 μs。本文对变幅杆振动20个振动周期内空化流场进行数值计算。

计算中空化流的物性参数取温度为30 ℃时的值，其中水和水蒸汽的密度分别为995.6 kg/m3和30.36 g/m3，水和水蒸汽的动力黏度分别为8×10-4kg/(m·s)和1.34×10-5kg/(m·s)，水的饱和蒸汽压psat为4247 Pa，水的表面张力系数σ为0.0717 N/m。假定水中不可凝结气体质量分数fg为1.5×10-5(默认值)。

3 计算结果与分析

在试件表面分别选择中心、边缘和径向距离5 mm处三个特征点，监视其压力和气体体积组分(vapor volumn fraction, VVF)随时间波动情况，其变化曲线分别如图5和图6所示。从图5和图6可看出，随变幅杆振动，试件表面各处压力和气体体积含量的波动具有周期性，而且压力波动具有显著的脉冲特征。除试件边缘外，其他两处压力可减小到水的汽化压力附近，表明试件表面附近流场可发生空化。试件表面附近流场空化表现为瞬态空化的特征。在试件中心处随压力的波动，空泡经历一次膨胀、收缩的振荡过程后，在超声的负压力区第二次膨胀，空泡体积进一步增加，VVF值达到50%，直至在随后出现的正压力区溃灭。空泡溃灭时，该处产生脉冲压力，峰值可达14 MPa。试样中心的脉冲压力每两个振动周期出现一次，这与该处的空泡溃灭频次相一致。在径向距离为5 mm处，一个振动周期内大部分空泡只经历一次膨胀过程就发生溃灭，VVF最大值为30%左右。与该处空泡溃灭的频率相对应，在此处每一个振动周期内均出现脉冲压力，其值约0.8 MPa。在试件边缘处，空化效果相对较弱，VVF值较小，空泡在两个振动周期内经过二次膨胀后溃灭，脉冲压力约0.5 MPa。

从不同监测点的空泡体积变化曲线(图6)和试样振动速度变化曲线(图3a)可看出，两者具有相同的变化趋势，表明试样振动加速度决定了磁致伸缩仪空化流空化变化趋势。当试样的加速度为正值时，其方向为拉伸液体方向，试样表面各处空泡体积组分不断增加；反之，试样表面空泡体积组分减小。

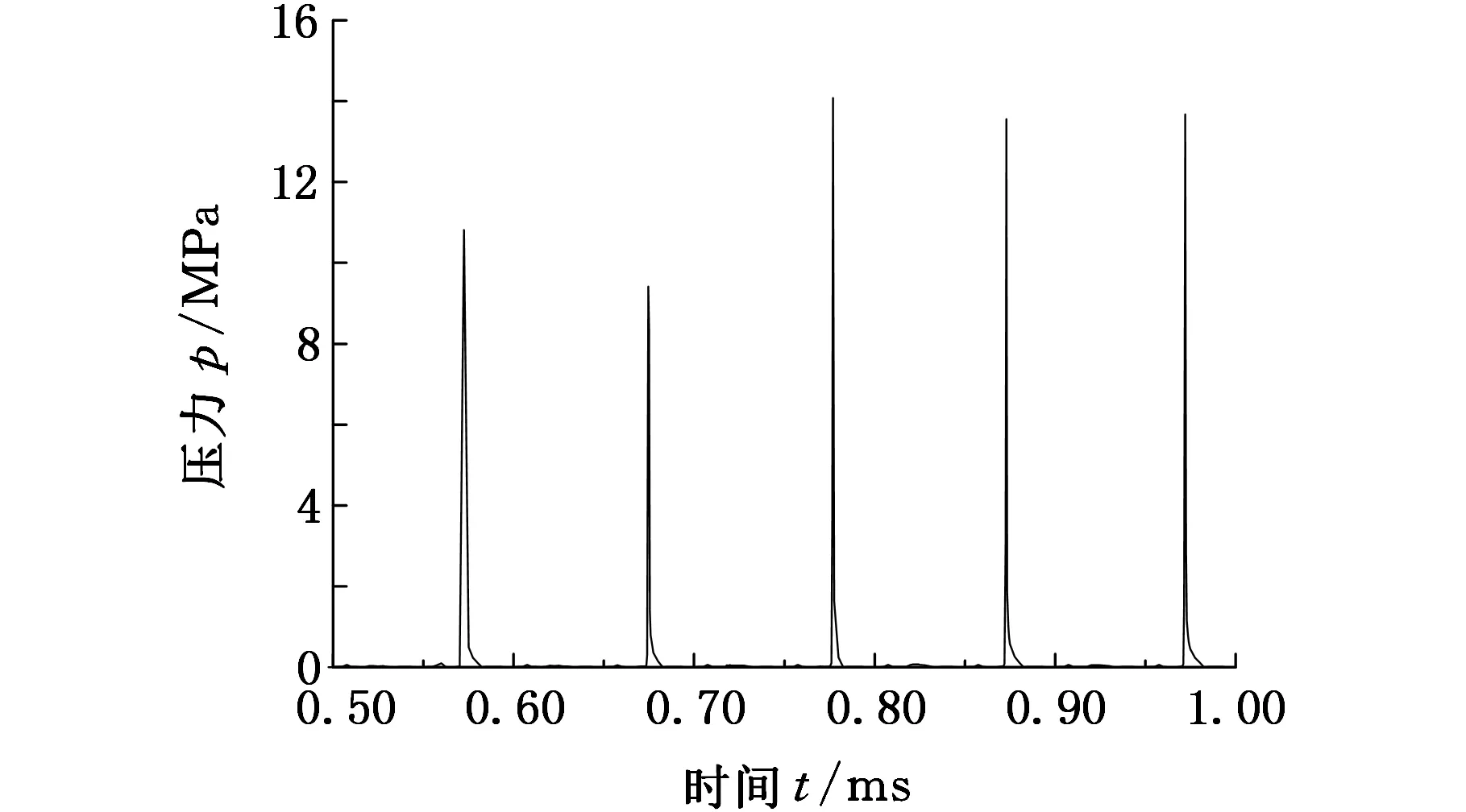
(a)中心

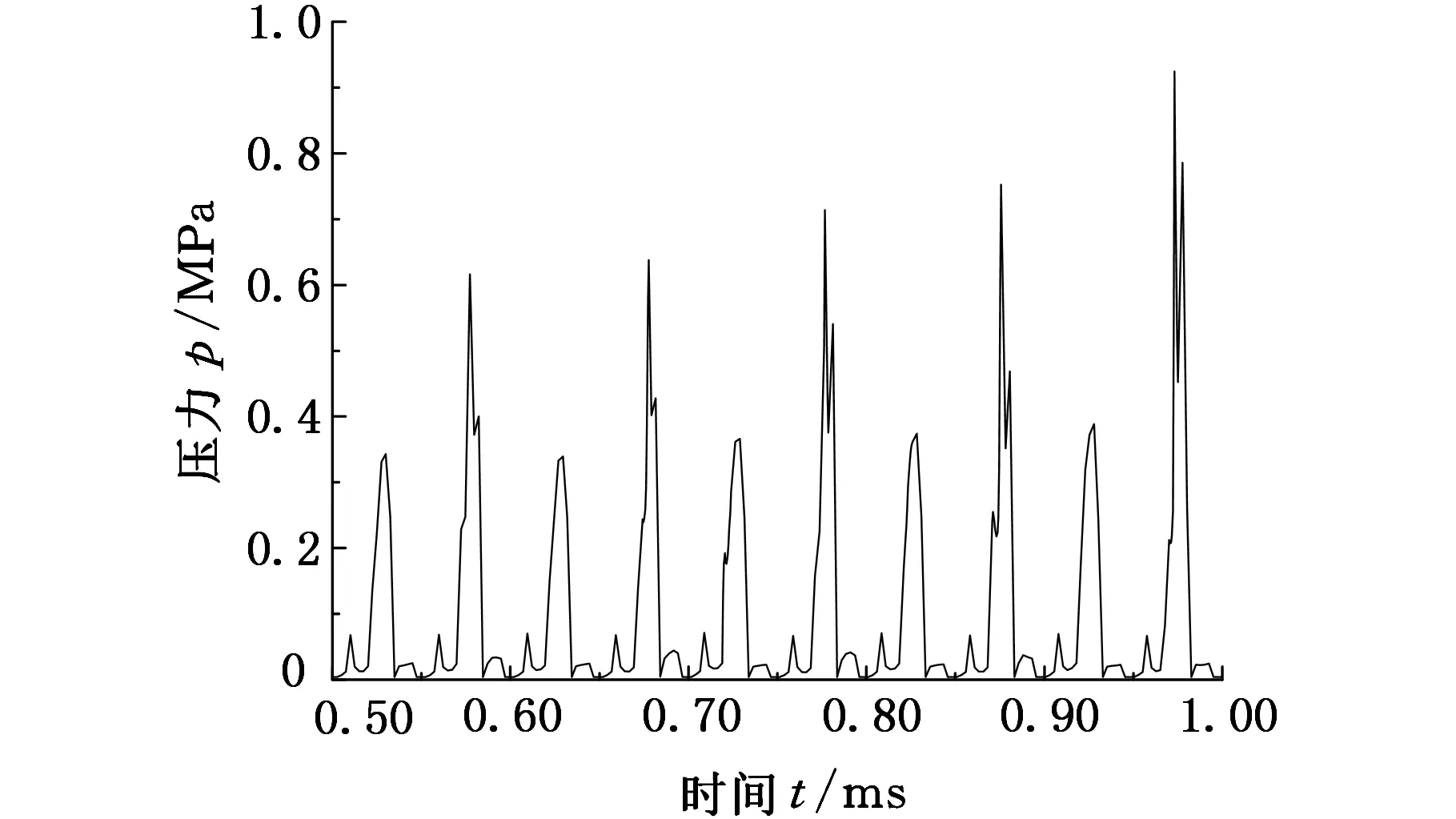
(b)径向距离5 mm处

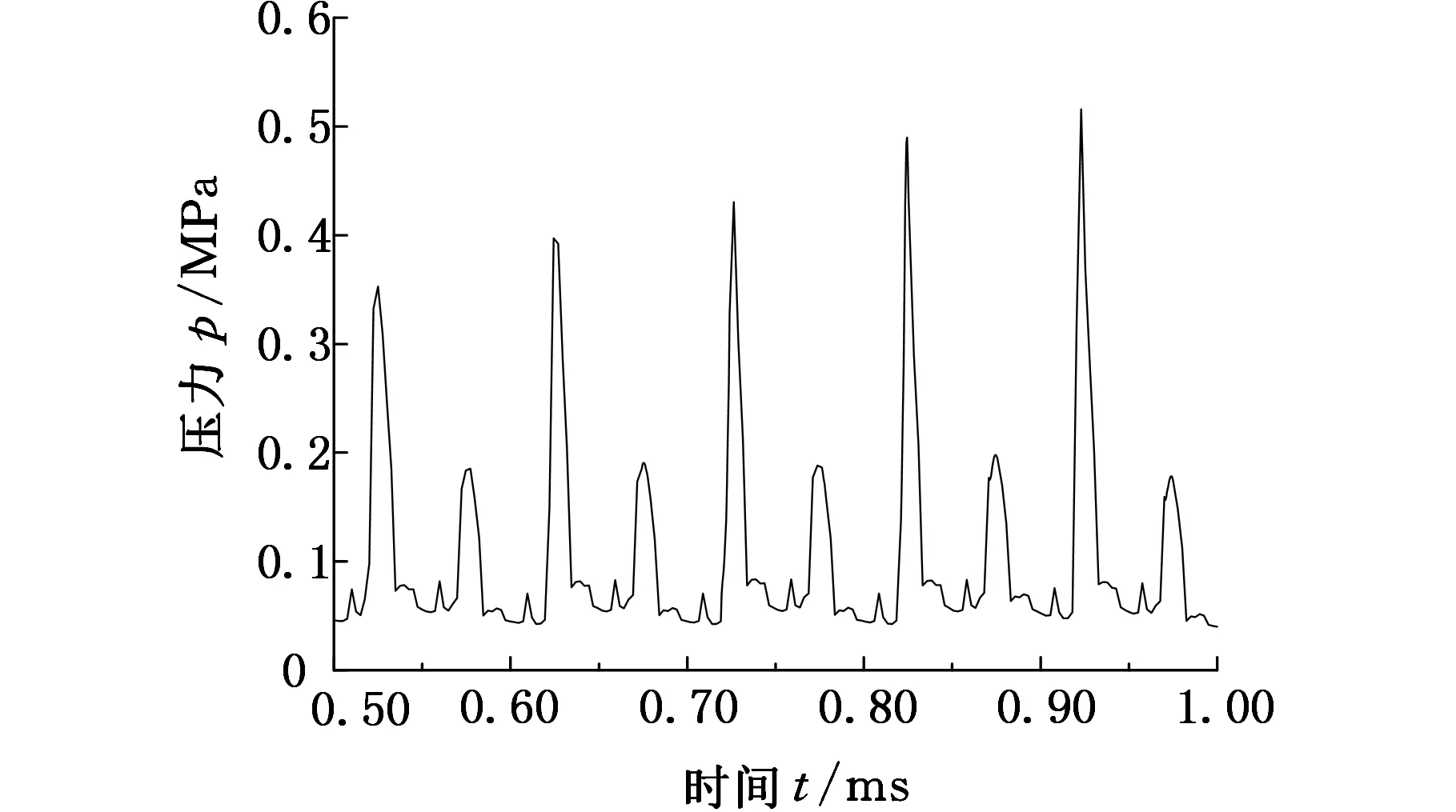
(c)边缘图5 试件表面不同位置压力随时间变化

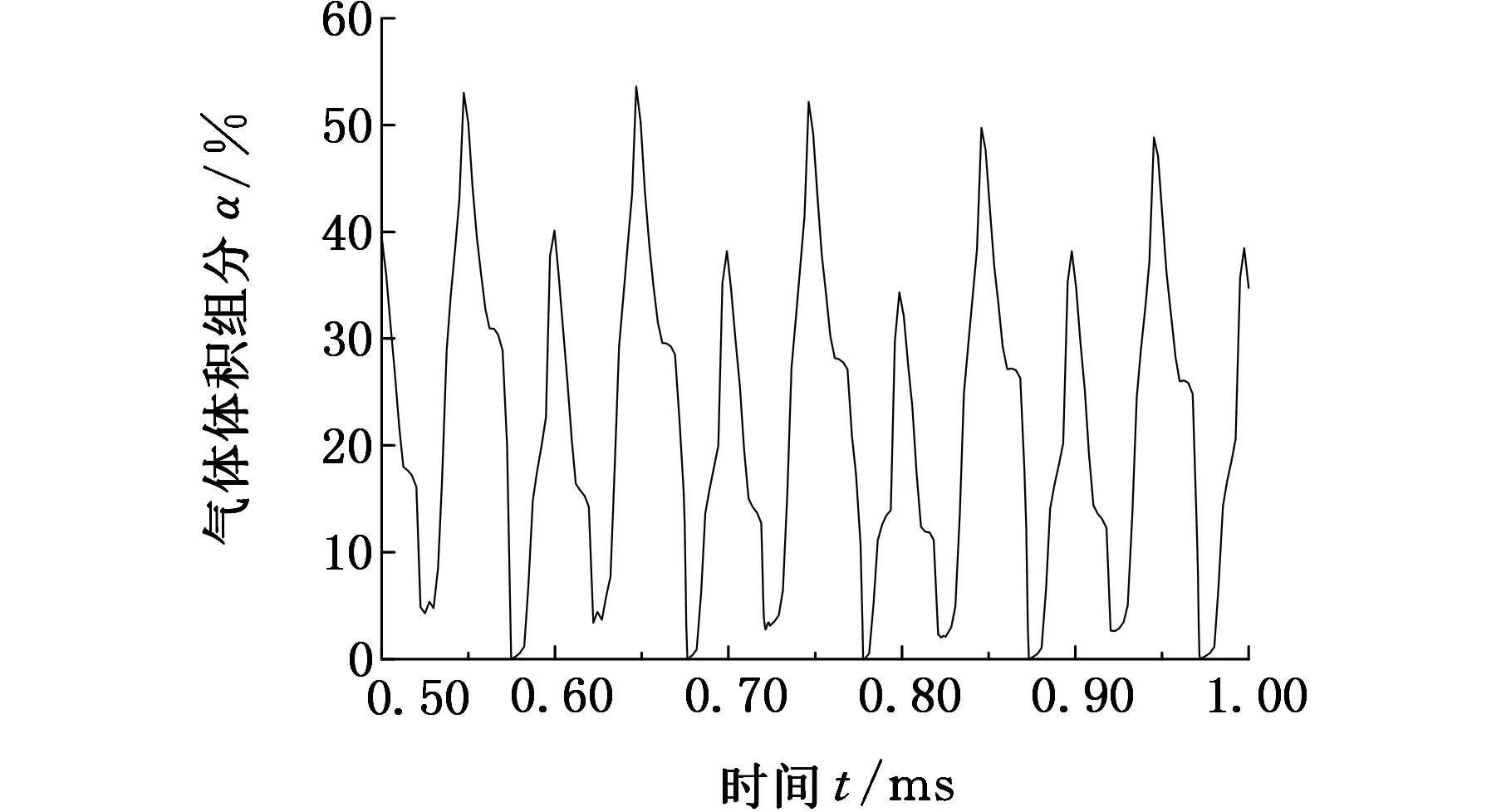
(a)中心

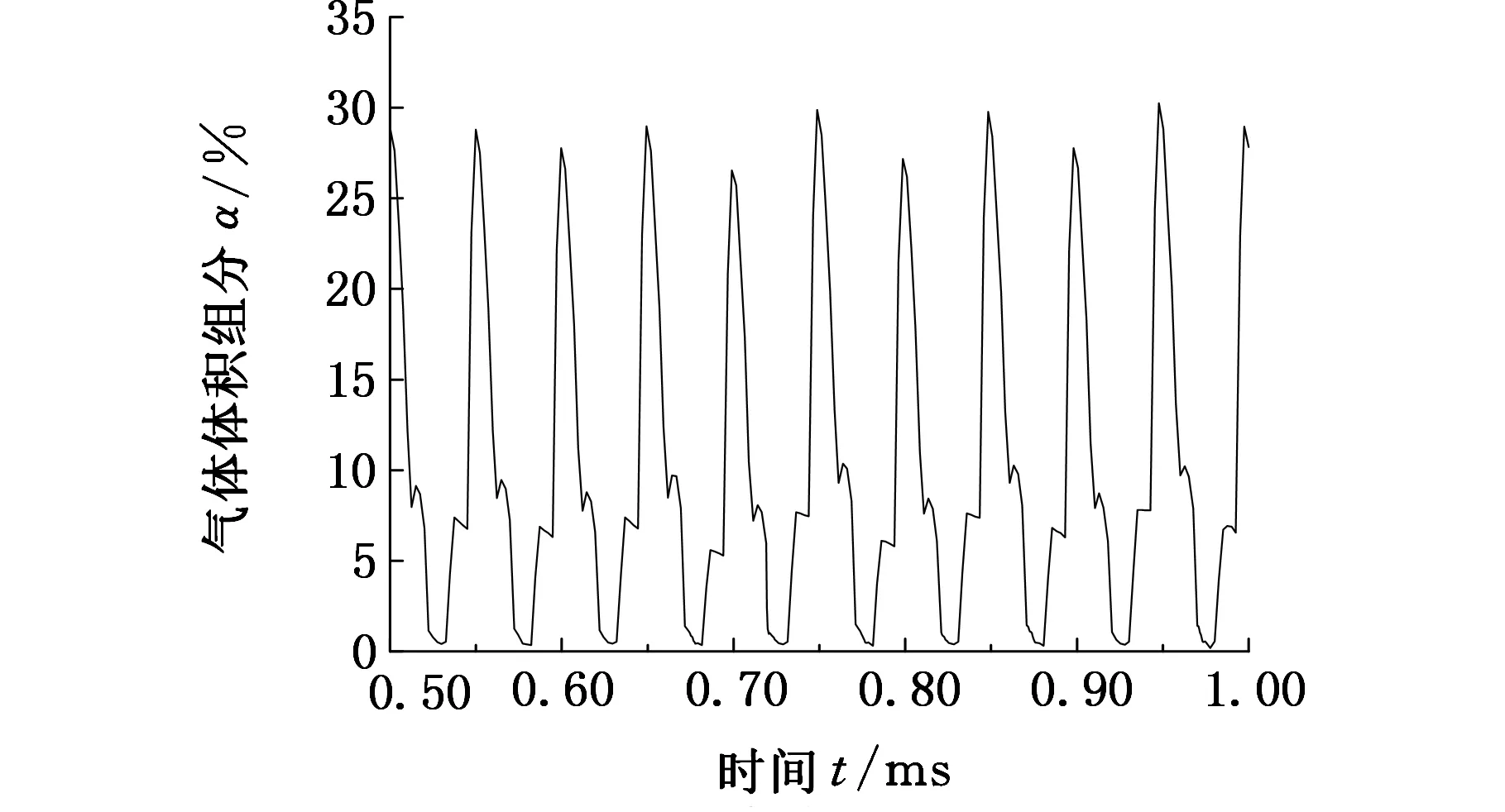
(b)径向距离5 mm处

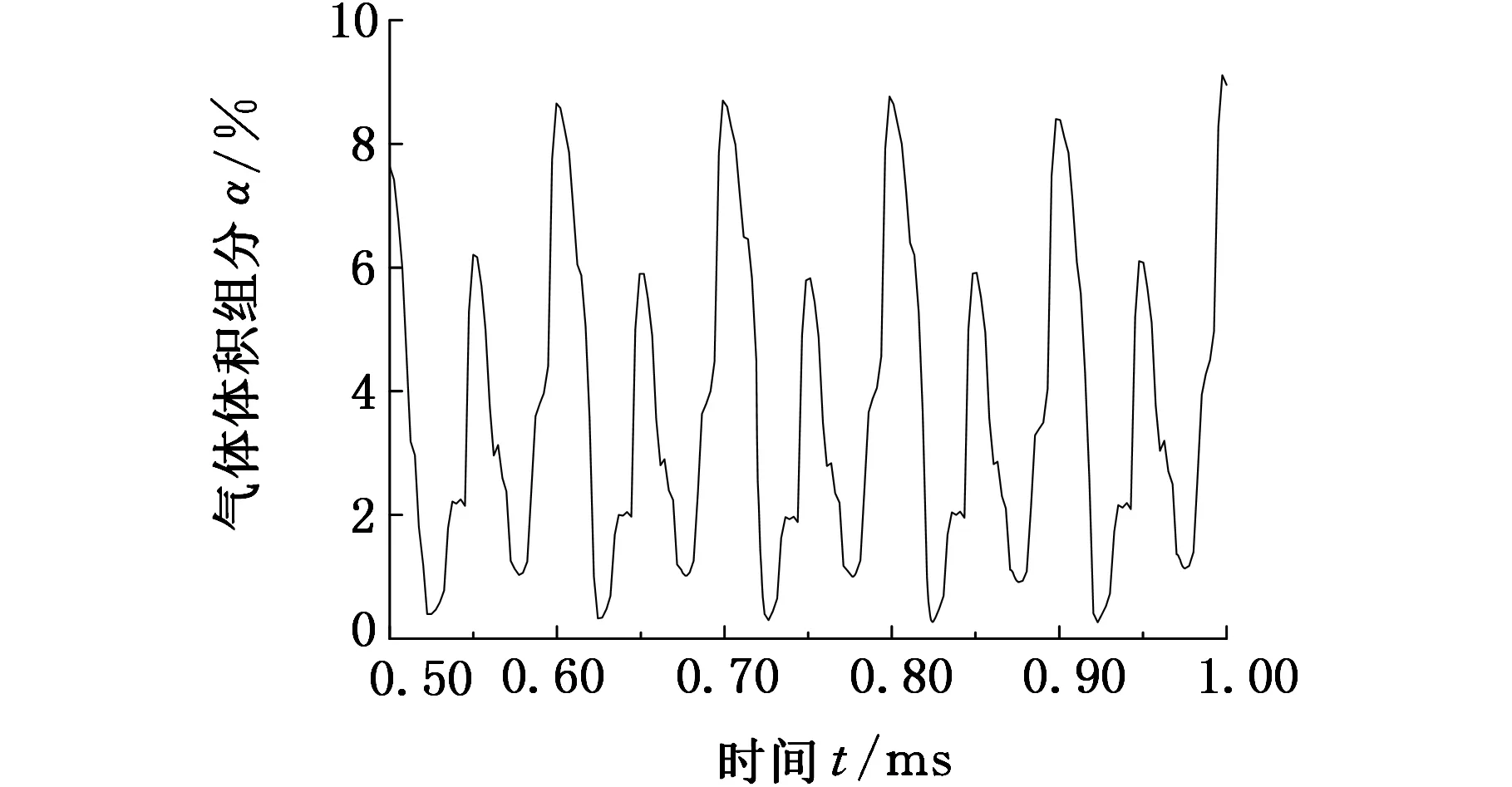
(c)边缘图6 试件表面不同位置气体体积组分随时间变化

当t=0.775 ms时，靠近试样的纵截面局部流场及试件表面的压力和VVF分布云图分别见图7和图8。当t=0.775 ms时，试件向下运动到平衡位置，此时加速度向下减小为0，速度达到最大。试件表面压力和VVF围绕试件中心近似呈环形分布，两者分布相对应。此刻，随压力增大，靠近试件表面空泡发生集中溃灭，产生脉冲压力，脉冲高压分布在试件中心和间隔的环形区域。但在脉冲高压区以外靠近试样局部流场处仍存在较低负压区，该区域有一定数量的空泡，VVF最大值可达33.5%。图7和图8表明即使在同一环形区域内，压力和VVF也不是均匀分布的，存在无规律断续脉动，这可能是由水流的脉动和水流运动影响空泡分布的均匀性及不均匀空泡溃灭所引起的。大于1 MPa的脉冲高压区分布在围绕试件中心半径约1.2 mm的近似半球范围内。由于试件表面压力分布近似呈环状分布，试样空蚀形貌应呈现环状分布的特征，这与大量的磁致伸缩仪空蚀实验结果相一致。试件中心产生较高的脉冲压力将使试件中心空蚀严重，但在外部的脉冲高压区域，断续出现的局部较高脉冲压力将会引起不均匀分布的空蚀坑的出现。

图9所示为相邻两周期内试样向下运动到平衡位置时试样表面沿径向压力分布。此时，试样压缩液体速度最大，试件表面空泡发生集中溃灭，产生脉冲压力。从图9可看出脉冲压力按间隔环形区域分布，且随试样振动在相邻的环形区域上交替出现。对于脉冲压力交替出现的相邻环形区域，其边界有重叠。在环形区域重叠处，每一个振动周期均出现一次脉冲压力，这与试样中心和各环形区域内部每两个振动周期出现一次脉冲压力的频次不同。从图9可看出径向距离为5 mm处恰好位于相邻环形区域重叠处，图5b中该处的压力变化体现了这一特征。

图7 t=0.775 s时纵向截面局部流场和试件表面的压力分布云图

图8 t=0.775 ms时纵向截面局部流场和试件表面的VVF分布云图

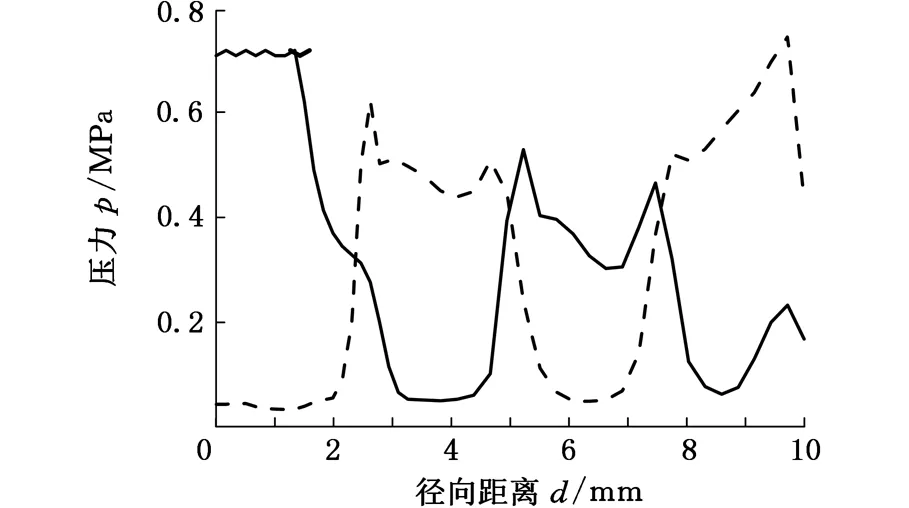
图9 相邻周期内空泡集中溃灭时试样表面径向压力分布

图10所示为相邻两个周期内试样振动加速度向上过程中径向VVF分布随时间的变化。图10中曲线1和曲线4分别为相邻两周期空泡集中溃灭时沿径向VVF分布。曲线1→3和曲线4→6表明，对于相邻两周期试样加速度指向拉伸液体的过程，靠近试样局部流场的VVF值不断增大。每一环形区域内空泡在两个振动周期内经过二次膨胀后发生溃灭。通过对比曲线1和曲线4可看出试样表面空泡溃灭发生在间隔环形区，且随试样振动，在相邻环形区域上空泡发生交替溃灭，这与试样表面脉冲压力的分布特征相对应。在空泡溃灭区以外的间隔环形区域内存在一定数量的空泡，其体积被压缩。

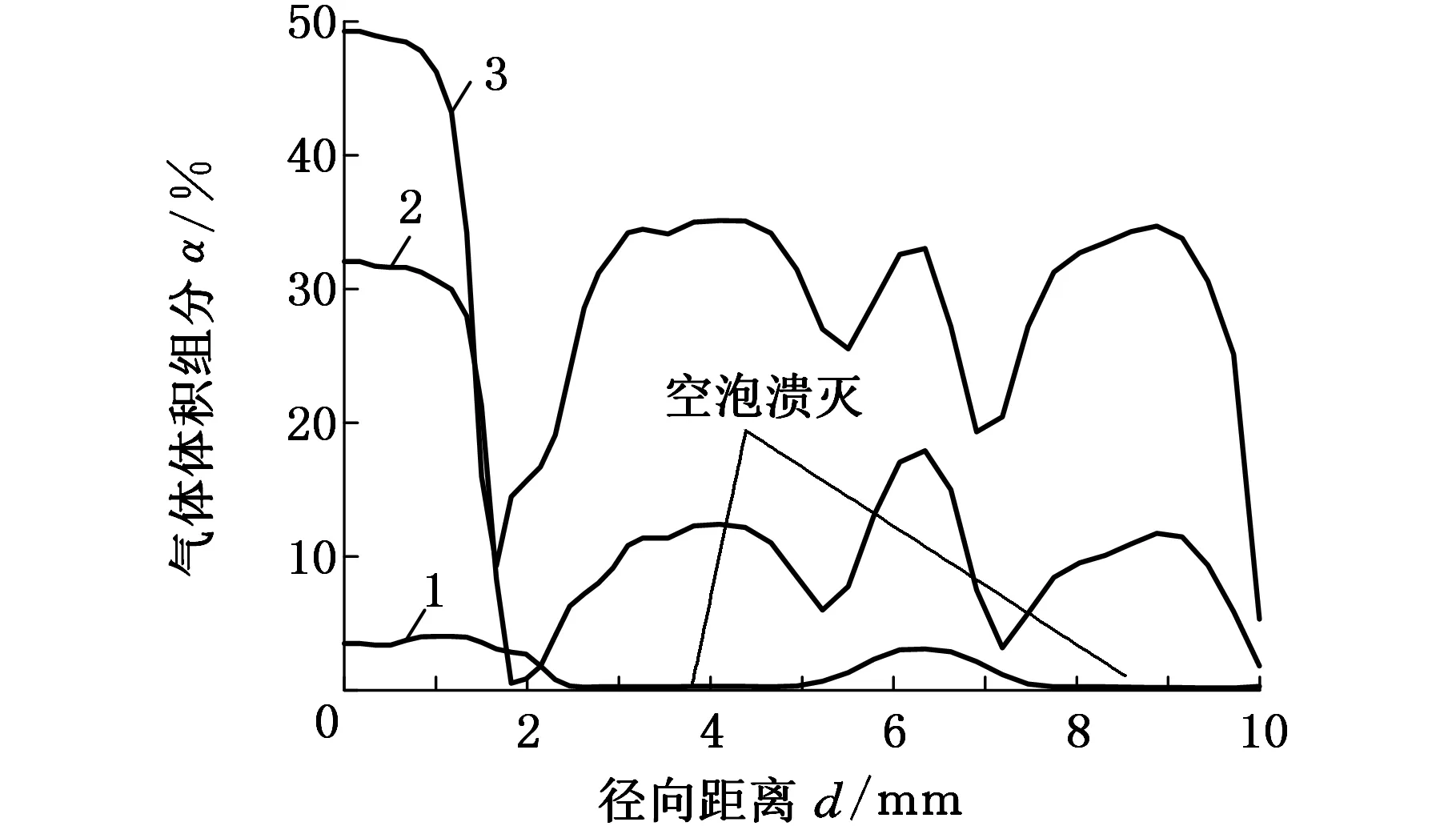
(a)

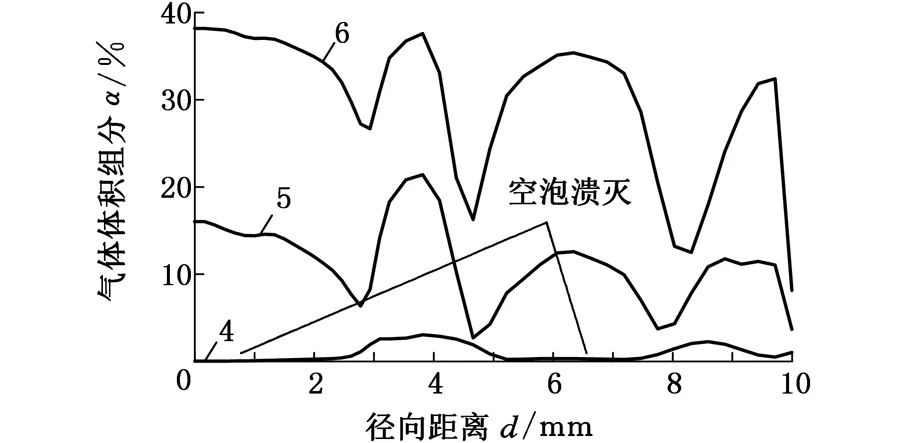
(b)图10 相邻周期内试件加速度向上过程中径向VVF分布变化

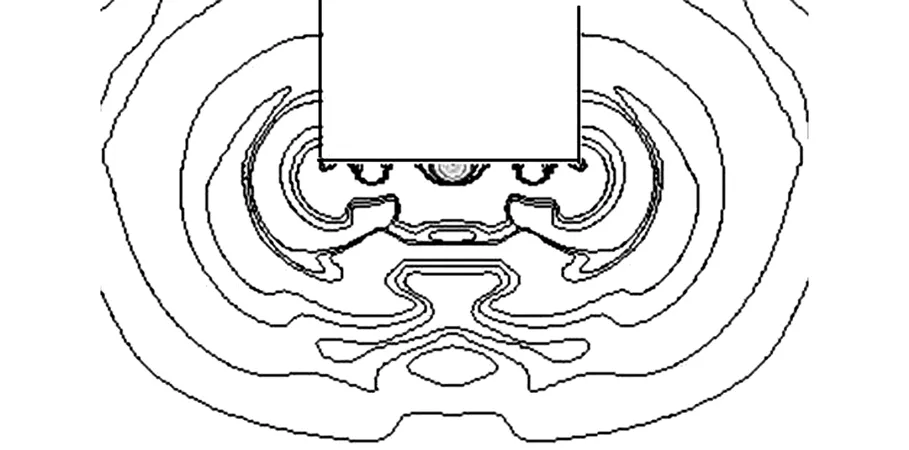
图11 t=0.775 ms时纵截面局部流场的压力等值线

当t=0.775 ms时，纵截面局部流场的压力等值线见图11。图11表明超声压力波不是以试件为中心呈球面波形传播的。由于磁致伸缩仪空化流场的空化程度不均匀和空泡溃灭使试件表面附近局部流场形成高低压区，试件表面可近似多个声波发生源，各声波传播时相互叠加和干扰。

图12所示为一个振动周期内在试件表面中心垂线上压力分布的变化。变幅杆振动频率为20 kHz，超声波波长为70 mm。图12表明在磁致伸缩仪超声空化流场中，随着距振动试样距离增加，声压快速衰减，压力的明显波动只发生在距试件表面约20 mm内，约为波长的1/3，验证了由变幅杆高频振动产生的超声波在空化流场传播过程中能量快速衰减。

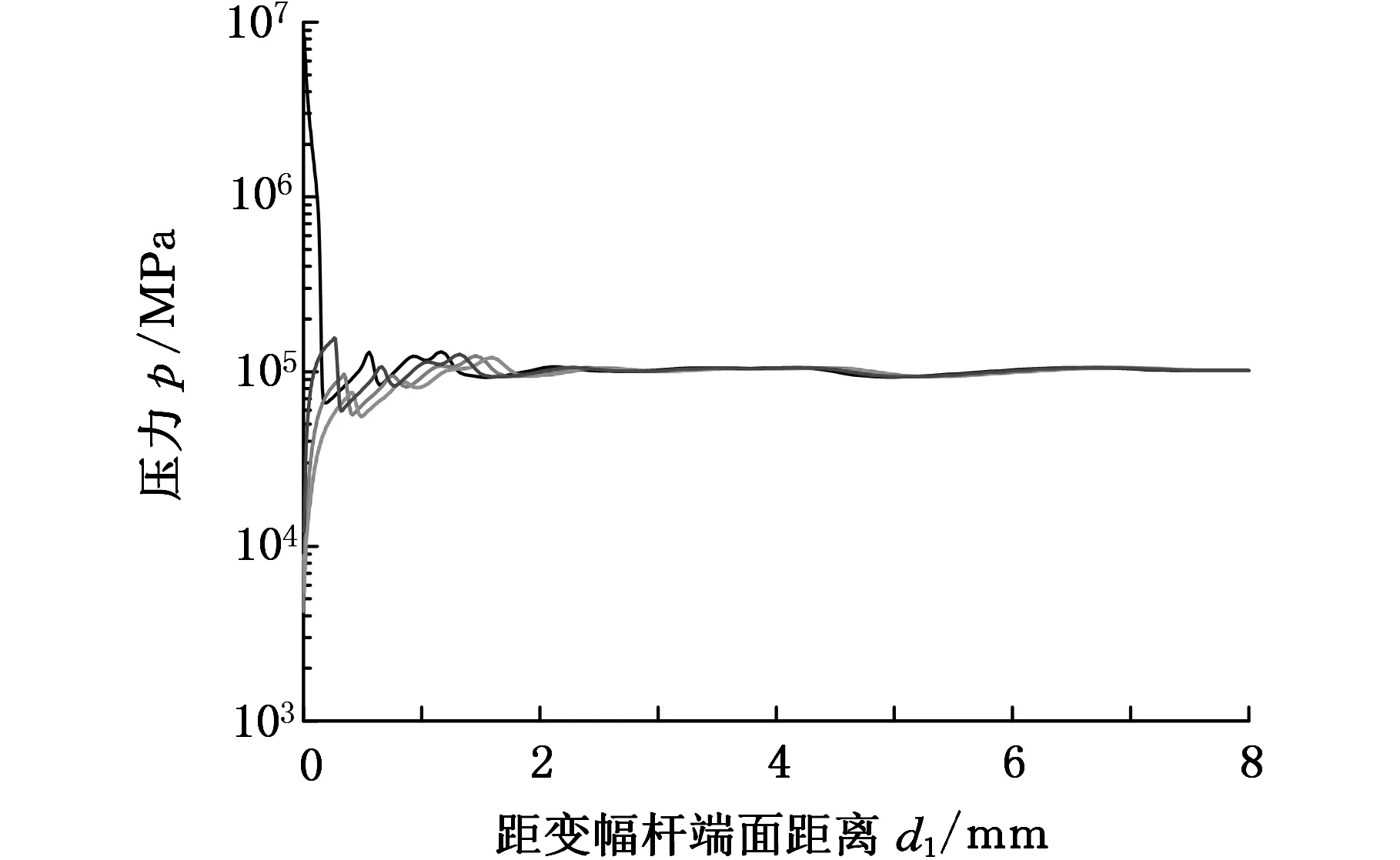
图12 某一周期内变幅杆端面垂线上压力变化

对于超声空化流场中超声波能量的快速衰减，除了超声波的扩散衰减和由液体黏滞性引起的吸收衰减因素外，在靠近变幅杆端面附近的空化区域内，空泡的生成、膨胀等空化过程吸收超声波能量及空泡对超声波传播的干扰等因素也会引起超声波的能量衰减。

4 结论

(1) 通过数值模拟，验证了磁致伸缩仪空化实验试样空蚀机理。变幅杆高频振动引起试件表面附近局部流场发生空化。随压力波动，当试件表面附近空泡溃灭时产生脉冲压力。在试样中心区域空化程度和脉冲压力作用效果显著，最大脉冲压力可达14 MPa。

(2)压力和VVF在试样表面近似呈环形分布。在同一环形区域内，压力和VVF存在无规律断续脉动。脉冲压力在间隔的环形区域形成，且随试样振动在相邻的环形区域上交替出现。

(3)在超声空化流场中，试件表面可近似多个声波发生源，各声波传播时相互叠加和干扰。声压随距试样距离增加快速衰减，压力明显波动只发生在距试件表面约20 mm内，约为波长的1/3。

[1] Philipp A, Lauterborn W. Cavitation Erosion by Single Laser-produced Bubbles[J]. Journal of Fluid Mechanics, 1998, 361: 75-116.

[2] 夏冬生, 张会臣, 于彦. 柴油机气缸套冷却水空化流的三维数值模拟[J]. 机械工程学报, 2011, 47(22):167-173. Xia Dongsheng, Zhang Huichen, Yu Yan. 3D Numerical Simulation of Cooling-water Cavitation Flow of Cylinder Liner for a Diesel Engine[J]. Journal of Mechanical Engineering, 2011, 47(22):167-173.

[3] Hattori S, Mikami N. Cavitation Erosion Resistance of Stellite Alloy Weld Overlays[J]. Wear, 2009, 267(11):1954-1960.

[4] Ahmed S M. Investigation of the Temperature Effects on Induced Impact Pressure[J]. Wear, 1998, 218(1):119-127.

[5] Benjamin T B, Ellis A T. The Collapse of Cavitation Bubbles and the Pressures Thereby Produced Against Solid Boundaries[J]. Philos. Trans. R. Soc., 1966, 260(1110):221-240.

[6] Leighton T G. The Acoustic Bubble[M]. London: Academic Press, 1997.

[7] Mørch K A. Erosion[M]. London: Academic Press, 1979.

[8] Bai Lixin, Xu Weilin, Zhang Faxing, et al. Cavitation Characteristics of Pit Structure in Ultrasonic Field[J]. Science in China (Series E: Technological Sciences), 2009,52(7):1974-1980.

[9] Burdin F, Tsochatzidis N A, Guiraud P, et al. Characterisation of the Acoustic Cavitation Cloud by Two Laser Techniques[J]. Ultrasonics Sonochemistry, 1999,6(1/2):43-51.

[10] Singhal A K, Athavale M M, Li H Y, et al. Mathematical Basis and Validation of Full Cavitation Model[J]. Journal of Fluid Engineering, 2002, 124(3):617-624.

[11] Menter F R. Two-equation Eddy-viscosity Turbulence Models for Engineering Applications[J]. AIAA Journal, 1994, 32(8):1598-1605.

(编辑 陈 勇)

3D Unsteady Numerical Simulation of Magnetostriction-induced Ultrasonic Cavitation Flow

Xia Dongsheng Sun Changguo Yu Yan Zhang Huichen

Dalian Maritime University, Dalia，Liaoning，116026

The magnetostriction-induced ultrasonic cavitation flow was numerically simulated by using a “Singhal full cavitation model” and SSTk-ωturbulence model with the dynamic mesh technique. The characteristics of ultrasonic cavitation flow and the cavitation erosion mechanism were revealed. The computational results show that pressure and vapor volume fraction (VVF) vary periodically on the specimen with vibration of the specimen. The lowest value of pressure fluctuation reaches the vapor pressure at the local flow field proximity to the specimen, where cavitation can occur. Pressure fluctuation presents a distinct pulse feature on the specimen surface, due to cavitation. Moreover, pressure and VVF were annularly distributed around the center on the specimen. However, they have irregular and discontinuous pulse in the annular zones. At the center of specimen, bubbles collapse leads to intense pulse pressure after twice oscillation, which can reach about 14 MPa. Pulse pressure was distributed in the interval annular zones and alternately occurs in the adjacent annular zones with vibration of the specimen. In the ultrasonic cavitation flow field, the specimen surface seems to be as several acoustic emission sources. The acoustic waves generate mutual superposition and interference. Pressure dramatically attenuates with increasing the distance to the specimen. The considerable pressure fluctuation occurs within the distance of about 20 mm to the specimen.

magnetostriction apparatus; computational fluid dynamics(CFD); cavitation; pulse pressure

2015-10-13

国家自然科学基金资助项目(51275064,50975036);辽宁省自然科学基金资助项目(2015020136)；中央高校基本科研业务费专项资金资助项目(3132013063)

TV131.3； O359.1

10.3969/j.issn.1004-132X.2016.22.014

夏冬生，男，1973年生。大连海事大学交通运输装备与海洋工程学院副教授。主要研究方向为机械摩擦磨损机理和润滑、计算流体力学。发表论文20余篇。孙昌国，男，1979年生。大连海事大学交通运输装备与海洋工程学院讲师。于 彦，女，1972年生。大连海事大学交通运输装备与海洋工程学院副教授。张会臣(通信作者)，男，1965年生。大连海事大学交通运输装备与海洋工程学院教授。