混合动力汽车电池内部状态预测的贝叶斯极限学习机方法

王 琪 孙玉坤 倪福银 陈泰洪 陈连玉 罗印升

1.江苏理工学院，常州，213001 2.南京工程学院，南京，211167



混合动力汽车电池内部状态预测的贝叶斯极限学习机方法

王 琪1孙玉坤2倪福银1陈泰洪1陈连玉1罗印升1

1.江苏理工学院，常州，213001 2.南京工程学院，南京，211167

针对混合动力汽车(HEV)电池内部状态预测问题，引入贝叶斯极限学习机(BELM)方法。对BELM的基本原理进行了详细介绍，在高级车辆仿真软件ADVISOR中采集HEV电池的各项性能参数，包括电压、电流、温度和内阻等。基于此，将BELM应用于电池的荷电状态(SOC)和健康状态(SOH)的预测，同时考虑电池老化对内部状态预测效果的影响。BELM预测结果表明：所设计的预测模型具有较高的精度，能够实时准确地预测出电池的SOC和SOH值。

贝叶斯极限学习机;混合动力汽车;荷电状态;健康状态

0 引言

电池作为混合动力汽车动力系统的关键部件，对整车系统的动力性、安全性以及经济性至关重要[1]。为保证电池性能良好，延长其使用寿命，需要对电池进行合理的管理与控制，但是前提必须是准确而又可靠地获得电池的内部状态[2]。

电池的内部状态主要分为荷电状态(state of charge,SOC)和健康状态(state of health,SOH)两个部分，其中SOC表征电池的剩余电量，可以用剩余电量除以电池的总容量表示[3]；SOH表征电池的老化程度，可以用老化电池的容量除以新电池的容量表示[4]。目前研究电池SOC的报道较多，其预测方法主要有安时计量法[5]、开路电压法[6]、内阻特性法[7]、卡尔曼滤波法[8]、模糊逻辑方法[9]、径向基函数(radial basis function,RBF)核神经网络法[10]和最小二乘支持向量机法[11]等，这些方法各有优缺点和使用范围，并不完全适用于混合动力汽车电池。相对于电池SOC的研究，研究电池SOH的报道则较少，主要方法包括卡尔曼滤波法[12]、样本熵方法[13]和神经网络模糊推理方法[14]等。电池SOC和SOH与其电压、电流、温度和内阻等参数有关，它们不能直接被测量，只能通过这些参数预测而得。另外，SOC和SOH不仅与电池的各种参数有关，而且两者之间还有着密切的关系，这种各个参数之间的复杂联系使得SOC和SOH的精确预测具有较高的难度[15]。

针对混合动力汽车电池SOC及SOH预测问题，极限学习机(extreme learning machine,ELM)提供了有效的解决方案。ELM是Huang等[16]提出的一种新的单隐含层前向神经网络(single hidden layer feed-forward neural network, SLFN)的学习机。ELM网络结构简单，学习速度快，泛化性能好，利用Moore-Penrose广义逆求解网络权重，可以随机产生输入层与隐含层间的连接权值及隐含层神经元的阈值，且在训练过程中无需调整，只需要设置隐含层神经元的个数，便可以获得唯一的最优解。贝叶斯极限学习机(Bayesian extreme learning machine,BELM)基于贝叶斯线性回归原理来优化极限学习机输出层的权重，它涵盖了贝叶斯模型和ELM的 全部优点，降低了计算成本，避免了通过引导等繁琐的方法建立置信区间。

文献[17]采用稀疏贝叶斯预测方法建立了SOH的预测模型，稀疏贝叶斯是贝叶斯方法的一种拓展，从该文献中可以看出，稀疏贝叶斯方法实现了SOH的准确预测，预测精度较高。文献[18]采用贝叶斯最小二乘支持向量机对锂电池的剩余寿命进行了概率性预测，贝叶斯方法很好地对最小二乘支持向量机的正则化参数和核参数进行了优化，这对电池剩余寿命的精确预测至关重要；另外，文献[19]针对锂离子聚合物电池的电量问题采用了非线性贝叶斯估计，锂离子聚合物电池是一种新型电池，贝叶斯方法在该文献中同样作为优化策略，其估计方法采用卡尔曼滤波法。因此，贝叶斯方法在电池内部状态预测中优化预测算法是可行的。

本文采用BELM方法对混合动力汽车电池进行了SOC和SOH的预测，在美国城市动态循环驱动工况(urban dynamometer driving schedule,UDDS)下进行了仿真实验验证。

1 贝叶斯极限学习机的基本原理

极限学习机属于单隐含层前向神经网络，其网络如图1所示，其基本原理见文献[20-21]。

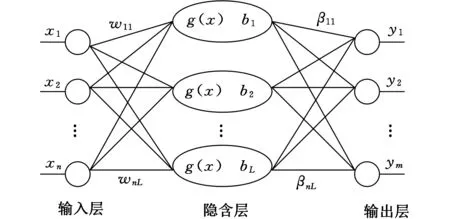
图1 极限学习机网络示意图

任何贝叶斯模型的实现都可以分为以下两步[22]：

(1)推断出模型参数的后验分布。模型的前验分布与似然函数的乘积是成比例的。设w为自由参数，D为数据空间，其计算公式为

P(w/D)=P(w)·P(D/w)

(1)

(2)对于一个新的输入x0，计算出模型的输出分布y0(为简单起见，这里只考虑一个输出)，可定义为w的后验分布的积分，即

P(y0/x0,D)=∫P(y0/x0,w)·P(w/D)dw

(2)

通过式(2)就可以预测出模型的输出[23]，具体实施过程见文献[24]。

贝叶斯方法使用了一些超参数的正则化，正则化项可以从模型参数的分布中得到，这样有助于减少模型的过度拟合；此外，置信区间的使用提高了模型输出的可靠性。

2 样本数据采集与处理

2.1 样本数据采集

HEV电池参数包括电压、电流、温度和内阻等，采用高级车辆仿真软件ADVISOR来获取这些参数。本文中混合动力汽车是使用铅酸蓄电池的标准小型车，其参数见表1。模拟行驶程序使用的测试工况选择美国城市动态循环驱动工况(UDDS)，UDDS被广泛使用于混合动力汽车性能测试，具有很强的代表性。开发后的混合动力汽车电池性能仿真结果如图2～图5所示。由于混合动力汽车的再生制动过程会对电池进行能量回馈，故图5中电池SOC曲线有小幅上升的区段。

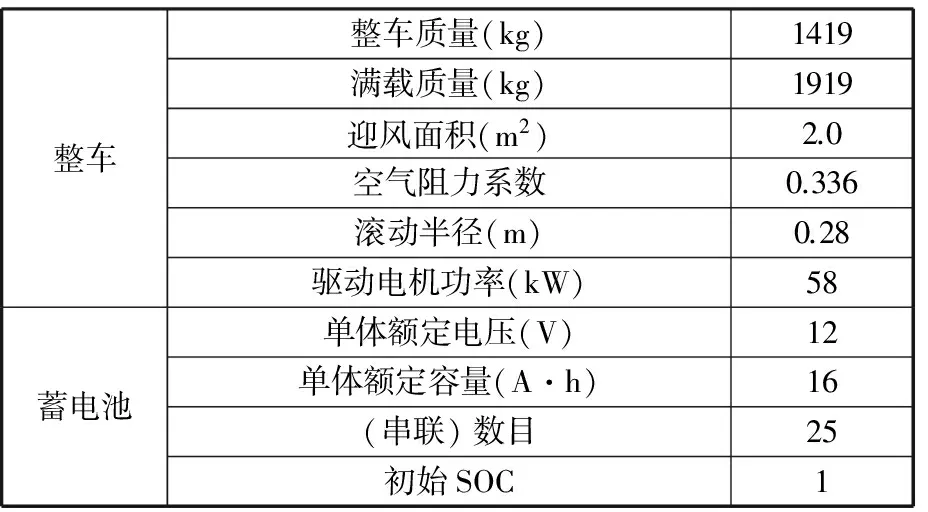
表1 标准小型车参数表

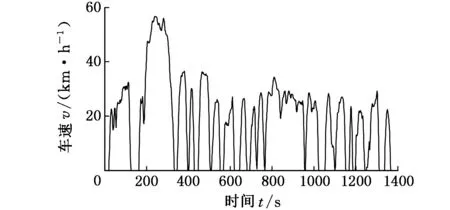
图2 UDDS工况

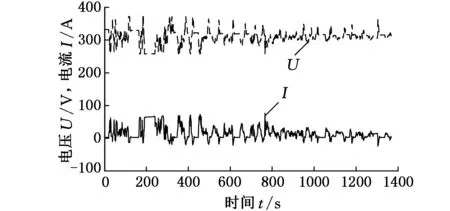
图3 电池电压和电流参数

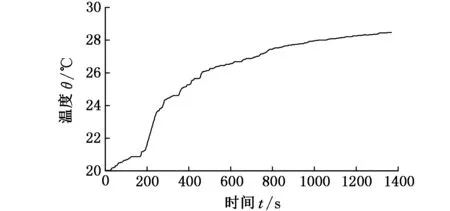
图4 电池温度参数

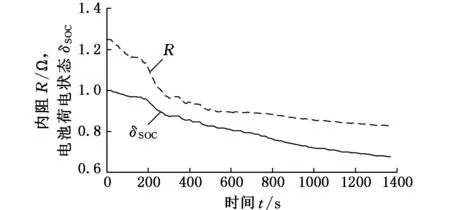
图5 电池内阻和SOC参数

2.2 样本数据采集

模拟测试工况被循环执行了2次，混合动力汽车总共行驶了2740 s。在模拟行驶过程中，使用频率为1 Hz的采样速度对电池各项参数进行了记录，总共获得2740组共13 700个数据。为了充分验证预测模型的有效性，对循环执行获得的样本数据进行排列，将第一次循环执行样本中的奇数项数据用于训练，第二次循环执行样本中的偶数项数据进行测试。

对于多参数问题的分析与计算，参数的基本度量单位首先要统一，这个观点同样适用于BELM。用于训练的样本数据集首先要被归一化，然后才能用于模型的训练[3]。同时，归一化的数据也有利于加快训练网络的收敛速度。

3 仿真实验

3.1 新电池SOC预测

所谓新电池即该电池未老化，其SOH值为100%。取电池的电压、电流、温度和内阻作为BELM的输入，输出为电池的SOC预测值。为了充分体现BELM的优越性，与当前研究得较多的最小二乘支持向量机方法(LS-SVM)进行比较研究。BELM的隐含层神经元的个数设置为30，考虑到LS-SVM正则化系数c和核参数σ2的选择会对预测结果具有较大的影响，采用贝叶斯证据框架(Bayesian evidence framework，BEF)算法优化LS-SVM，BEF的优化路径采用单纯形法。两种方法的预测结果如图6和图7所示。

不难看出，BEF-LS-SVM预测模型在起始和末端时刻的预测能力较强，而在中间时刻预测能力较差，这是由于中间时刻能量回馈较多，SOC的变化趋势不断发生变化，BEF-LS-SVM预测模型未能及时响应；BELM的预测效果明显优于BEF-LS-SVM，其预测值与真实值咬合得更加紧密。另外，尽管电池存在能量回馈的现象，BELM的预测模型依然具有较高的跟踪性能。

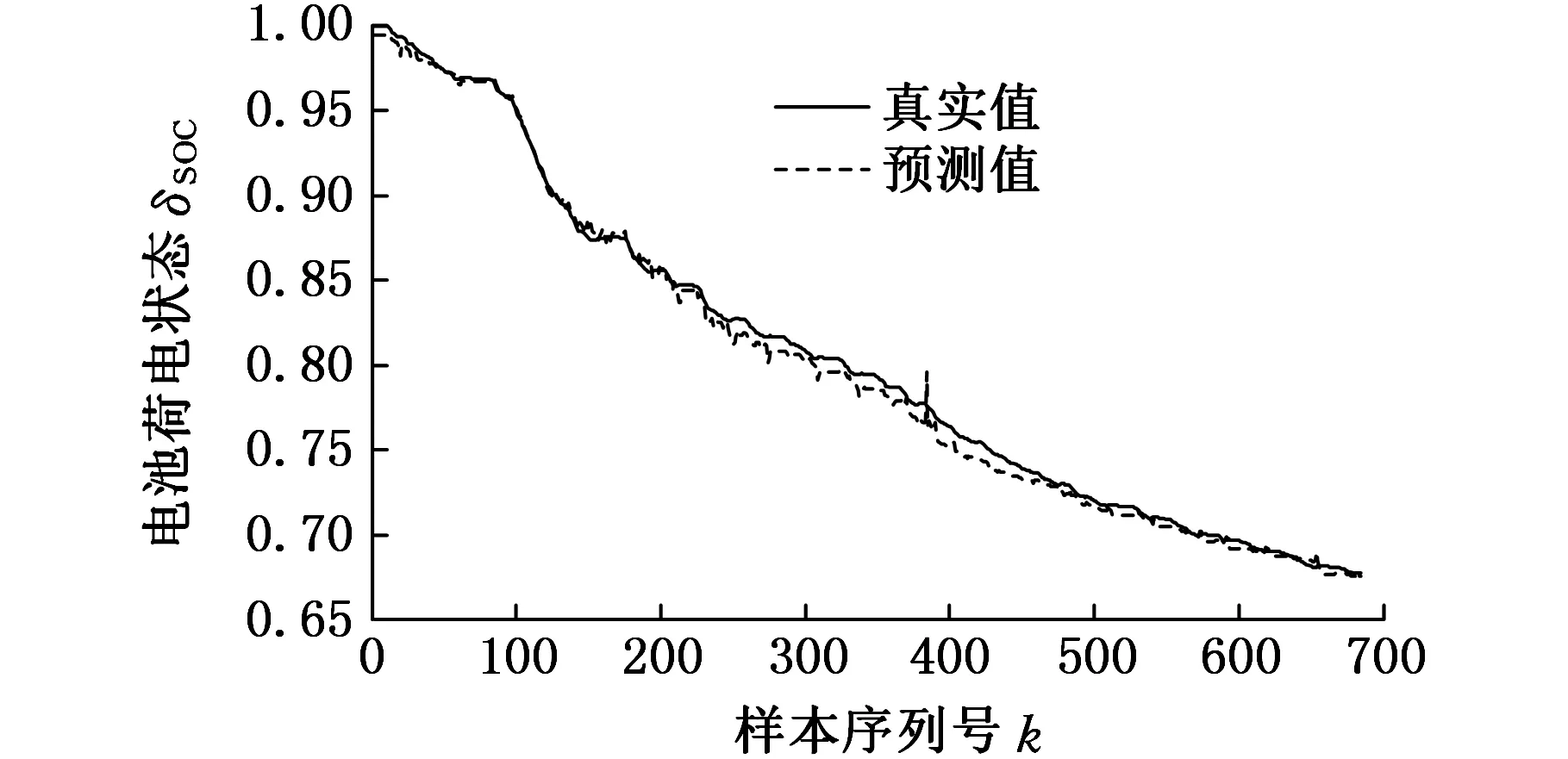
图6 基于BEF-LS-SVM的预测结果

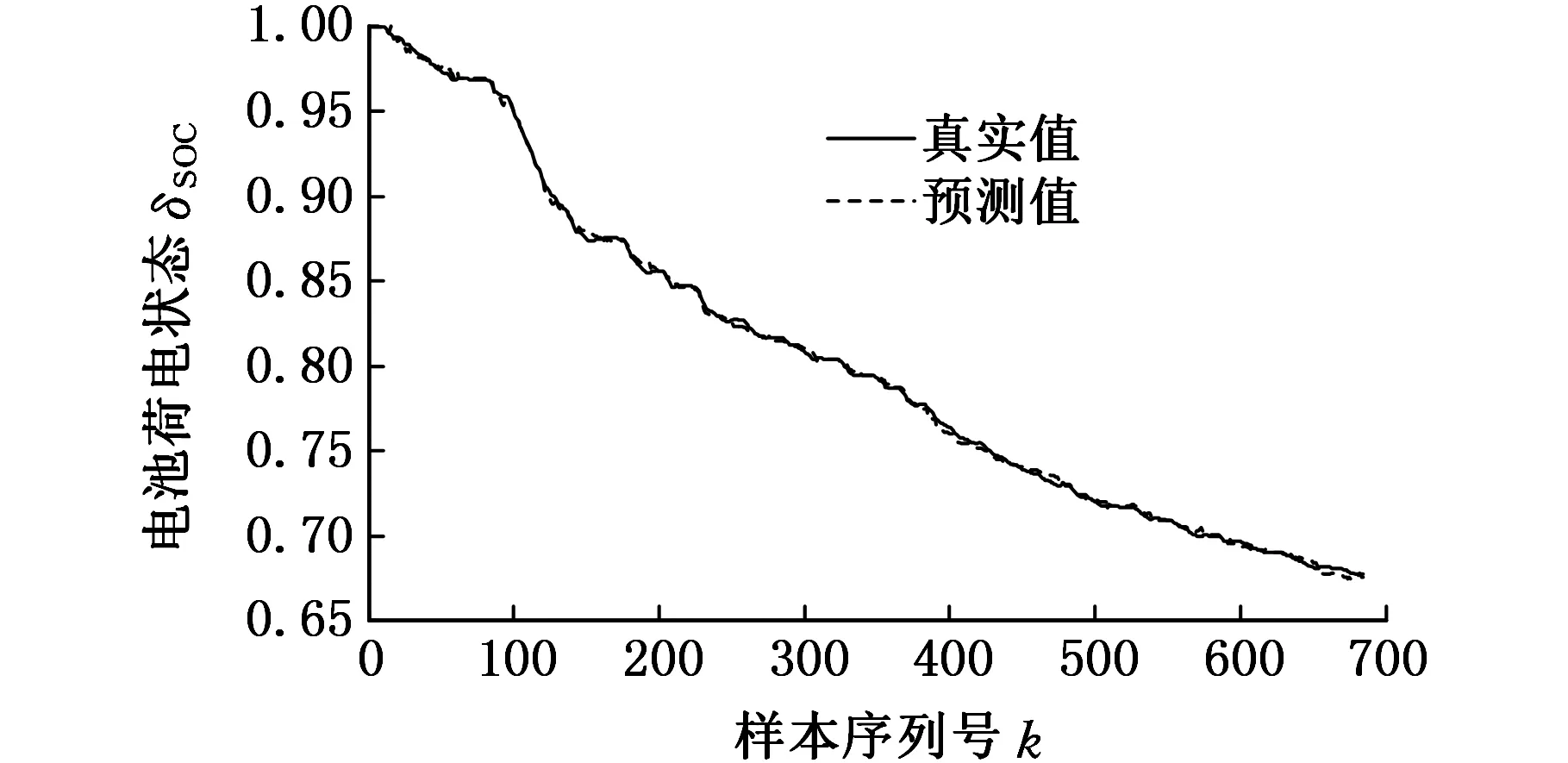
图7 基于BELM的预测结果

为了进一步说明BEF-LS-SVM和BELM所建预测模型的优劣，将预测模型绝对误差(absolute error, AE)和相对误差(relative error, RE)作为评价指标来评价两种预测模型，绝对误差EA和相对误差ER的定义分别为

(3)

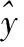
两种方法的预测误差如图8和图9所示。可以发现，不管是绝对误差还是相对误差，BELM预测模型的误差最大值均约为BEF-LS-SVM预测模型的1/3，误差分布得更加密集，因此，BELM预测模型的性能更加优越。

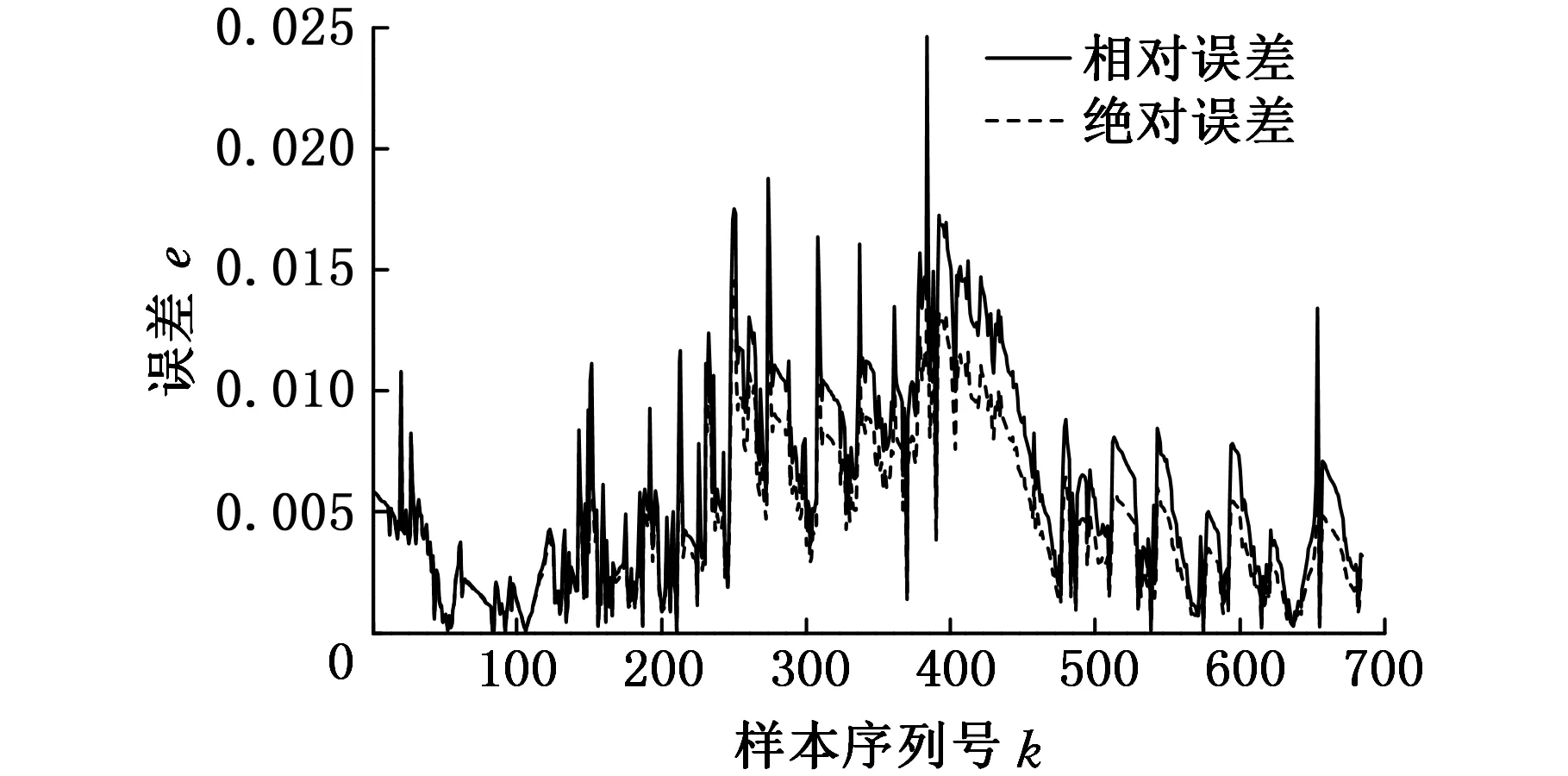
图8 基于BEF-LS-SVM的预测误差

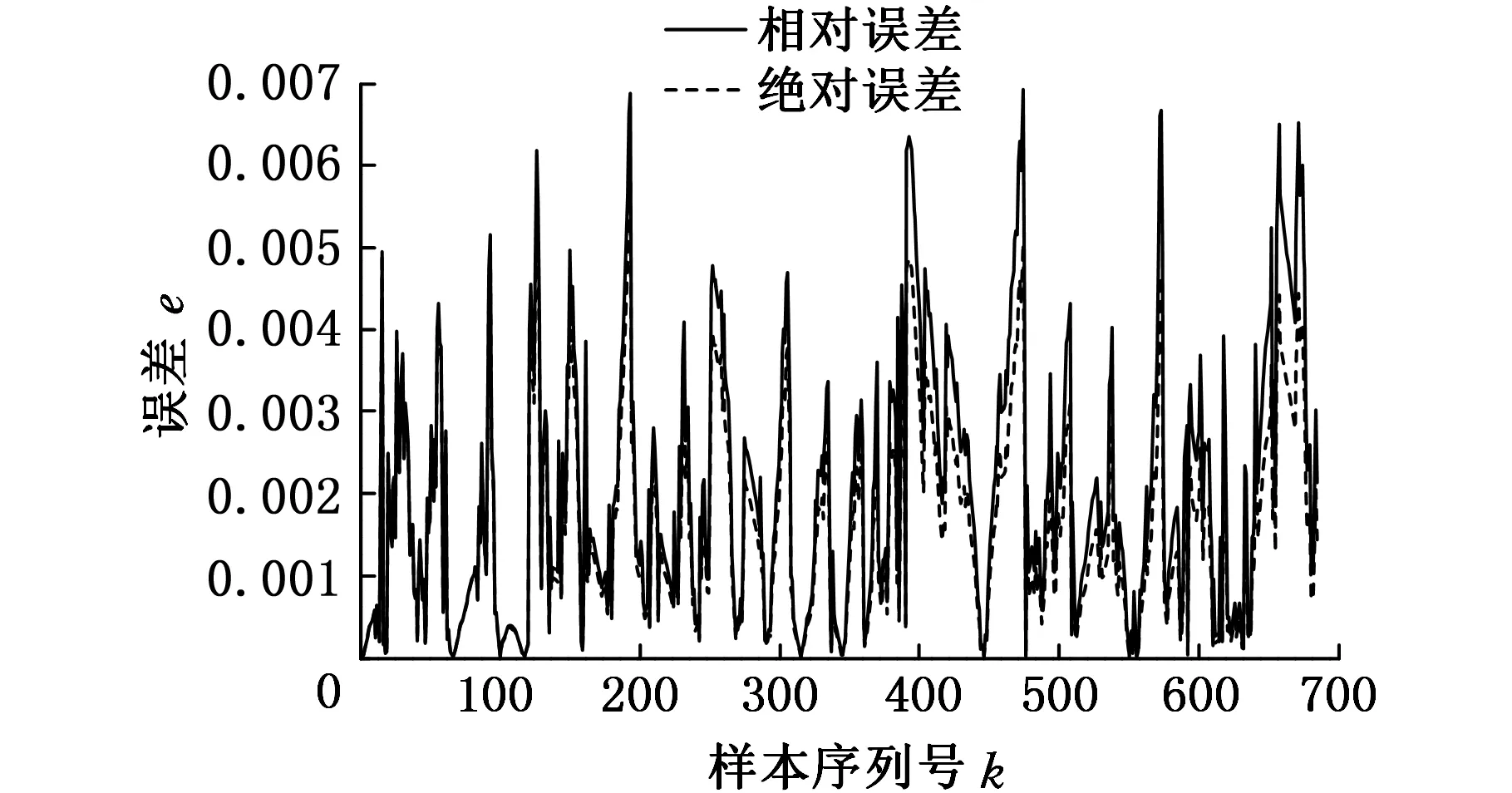
图9 基于BELM的预测误差

3.2 老化电池SOC预测

电池老化的程度由SOH来表征，老化后的电池容量会降低，内阻会变大，其SOC值下降得更快，从而降低了可提供的最大功率，因此，电池SOH对SOC的预测有着至关重要的影响。取两种不同SOH的电池进行SOC预测，其电池参数见表2。

表2 两种容量电池参数

由于BELM预测模型的效果较好，故采用BELM来对2种不同SOH的电池进行SOC预测，2种模型的预测结果和误差如图10～图13所示。

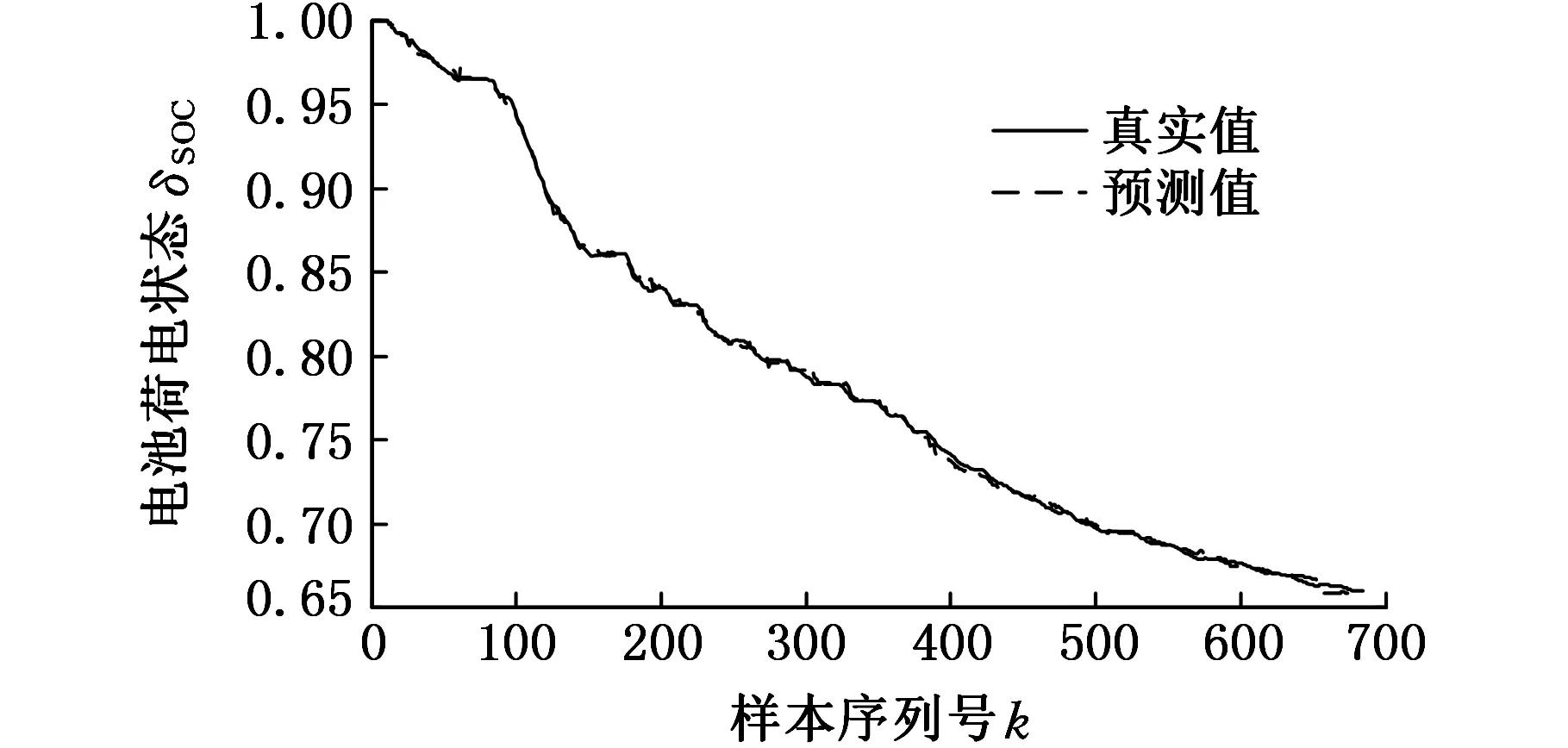
图10 SOH值为90%时的SOC预测结果

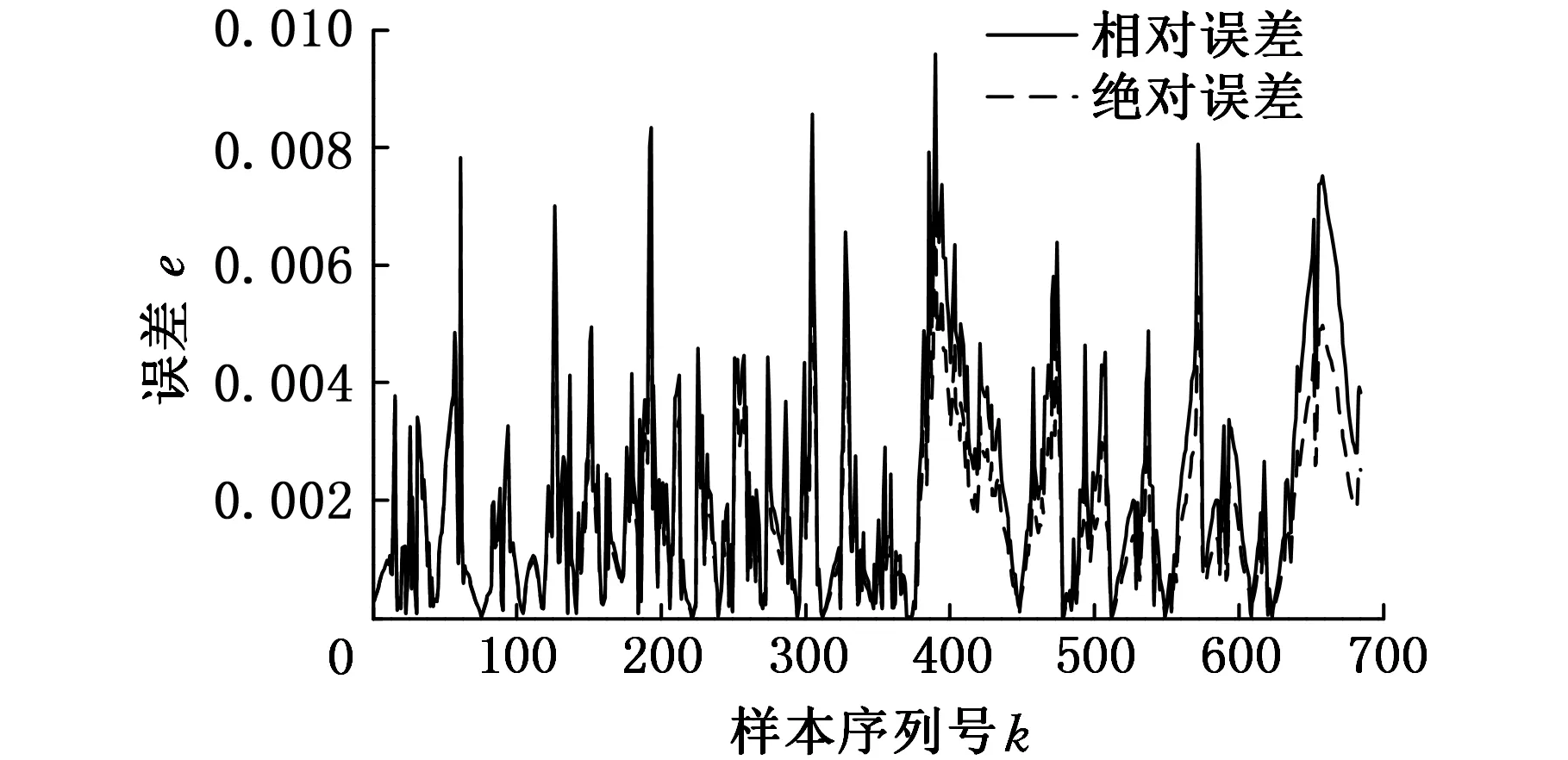
图11 SOH值为90%时的SOC预测误差

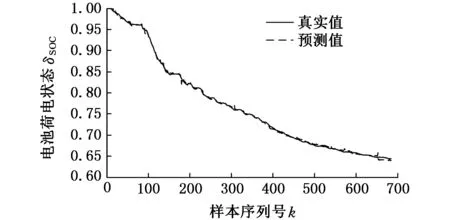
图12 SOH值为80%时的SOC预测结果

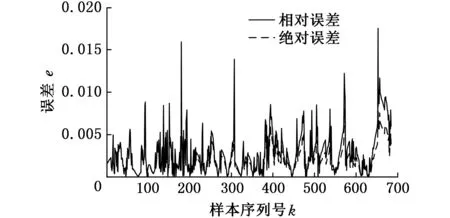
图13 SOH值为80%时的SOC预测误差

从图10～图13中不难发现，随着电池的老化(SOH值的降低)，电池SOC值下降的幅度有所增大，其预测值与真实值之间偏离的幅度也越来越大，同时伴随着预测误差的不断增大，出现这种情况的原因是老化后的电池其内部参数发生了变化(容量变小，内阻增大等)。尽管如此，基于BELM的老化电池SOC预测效果依然保持着较高的预测精度，即使当SOH值为80%时，绝对误差和相对误差的最大值仅约为2%。

3.3 电池SOH预测

对于老化电池，在相同条件下，其内阻变化往往比其他参数表现得更为敏感，这是由于内阻是电池受老化影响的主要参数之一，故可以根据内阻的变化来预测出电池的SOH值。内阻值的确定同样可以采用BELM算法对老化电池的内阻进行预测，BELM的输入为电池电压、电流、温度和SOC，输出则为内阻，具体预测过程与SOC一样，不再赘述。SOH值的计算公式如下：

(4)

其中，REOL为电池寿命终结时内阻，IEEE1188-1996中明确规定，当电池的容量下降到80%，即δSOH<80%时，就应该更换电池[25]。R表示电池的当前内阻，Rnew表示新电池的内阻。根据表2可以得到REOL为1.95 Ω，Rnew为1.25 Ω。在相同温度条件下，取不同容量的电池内阻，结合式(4)对电池SOH进行预测。分别取温度为25 ℃和28 ℃、SOH值为80%和90%时的老化电池对SOH进行预测，预测结果见表3。

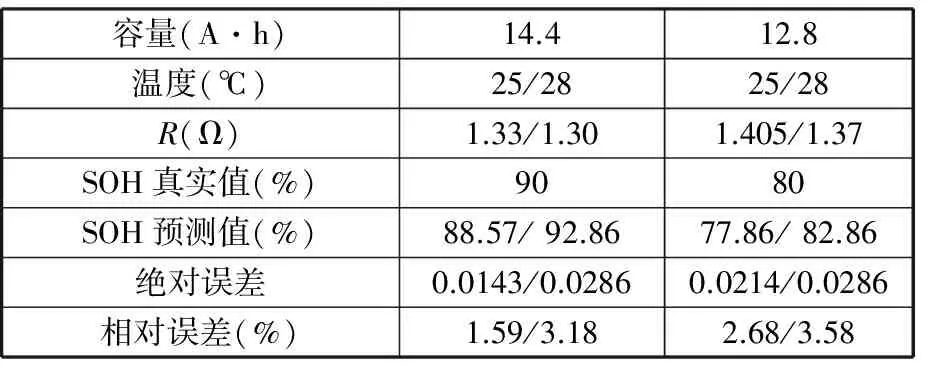
表3 SOH预测结果

从表3中可以看出，在一定温度范围内，随着温度的升高，电池内阻会降低，不管在25 ℃还是28 ℃条件下，SOH的预测值与真实值偏离程度均较小。另外，随着电池老化程度的加深，SOH的预测误差也会随之增大，尽管如此，在电池寿命终结，即SOH值为80%时，预测模型的相对误差最大值仅为3.58%，预测精度较高。

4 结论

(1)采用BELM对混合动力汽车电池内部状态(SOC和SOH)的预测是可行的，且模型预测性能良好。

(2)电池老化程度越深(即SOH值越小)，SOC和SOH的预测效果越差。

(3)BELM方法同样可以适用于电池其他参数的预测，比如内阻和容量等。

(4)本文方法在仿真过程中预测效果较好，精度较高。但是，在实际实验中会存在各种干扰和随机因素，今后将研究其他预测方法与BELM方法联合使用，进行优势互补，如样本熵、稀疏贝叶斯等。

[1] 戴海峰, 孙泽昌, 魏学哲.利用双卡尔曼滤波算法估计电动汽车用锂离子动力电池的内部状态[J].机械工程学报, 2009, 45(6): 95-101. Dai Haifeng, Sun Zechang, Wei Xuezhe. Estimation of Internal States of Power Lithium-ion Batteries Used on Electric Vehicles by Dual Extended Kalman Filter[J]. Journal of Mechanical Engineering, 2009, 45(6): 95-101.

[2] 雷肖, 陈清泉, 刘开培, 等.电动车蓄电池荷电状态估计的神经网络方法[J].电工技术学报, 2007, 22(8): 155-160. Lei Xiao, Chen Qingquan, Liu Kaipei, et al. Battery State of Change Estimation Based on Neural-network for Electric Vehicles[J]. Transactions of China Electrotechnical Society, 2007, 22(8): 155-160.

[3] 雷肖,陈清泉,刘开培,等.电动车电池SOC估计的径向基函数神经网络方法[J].电工技术学报, 2008, 23(5): 81-87. Lei Xiao,Chen Qingquan, Liu Kaipei, et al. Radial-based-function Neural Network Based SOC Estimation for Electric Vehicles[J]. Transactions of China Electrotechnical Society, 2008, 23(5): 81-87.

[4] Kong S N，Moo C S，Chen Y P，et al.Enhanced Coulomb Counting Method for Estimating State-of-charge and State-of-health of Lithium-ion Batteries[J].Applied Energy，2009，86(9)：1506-1511.

[5] 徐欣歌, 杨松, 李艳芳,等.一种基于预测开路电压的SOC估算方法[J].电子设计工程,2011,19(14): 127-129. Xu Xinge, Yang Song, Li Yanfang, et al. A Method of SOC-estimate Based on Forecast of Open-circuit Voltage[J]. Electronic Design Engineering, 2011, 19(14): 127-129.

[6] 李哲, 卢兰光, 欧阳明高. 提高安时积分法估算电池SOC精度的方法比较[J].清华大学学报(自然科学版), 2010, 50(8): 1293-1296. Li Zhe, Lu Languang, Ouyang Minggao. Comparison of Methods for Improving SOC Estimation Accuracy through an Ampere-hour Integration Approach[J]. Journal of Tsinghua University(Science and Technology), 2010, 50(8): 1293-1296.

[7] 朱元, 韩晓东, 田光宇. 电动汽车动力电池SOC预测技术研究[J]. 电源技术, 2000, 24(3): 153-156. Zhu Yuan, Han Xiaodong, Tian Guangyu. Research on Estimation Technology of Traction-battery SOC for Electric Vehicle[J]. Chinese Journal of Power Sources, 2000, 24(3): 153-156.

[8] Hu X, Li S, Peng H, et al. Robustness Analysis of State of Charge Estimation Methods for Two Types of Li-ion Batteries[J]. Journal of Power Soueces, 2012, 217(11): 209-219.

[9] Hu X, Li S, Yang Y. Advanced Machine Learning Approach for Lithium-ion Battery State Estimation in Electric Vehicles[J]. IEEE Transactions on Transportation Electrification, 2015, 99: 1-10.

[10] 刘瑞浩, 孙玉坤, 陈坤华. 电动汽车SOC利用BP神经网络模型预测方法研究[J]. 电测与仪表, 2011, 48(3): 34-37. Liu Ruihao, Sun Yukun, Chen Kunhua. BP Neural Network Model Estimation on State of Charge for Electric Vehicle[J]. Electrical Measurement and Instrumentation, 2011, 48(3): 34-37.

[11] Hu Xiaosong, Sun Fengchun. Fuzzy Clustering Based Multi-model Support Vector Regression State of Charge Estimator for Lithium-ion Battery of Electric[C]//International Conference on Intelligent Human-Machine Systems and Cybernetics.Hangzhou,2009:392-396.

[12] Zou Yuan, Hu Xiaosong, Ma Hongmin, et al. Combined State of Charge and State of Health Estimation over Lithium-ion Battery Cell Cycle Lifespan for Electric Vehicles[J]. Journal of Power Sources, 2015, 273: 793-803.

[13] Hu Xiaosong, Li S E, Jia Zhenzhong, et al. Enhanced Sample Entropy-based Health Management of Li-ion Battery for Electrified Vehicles[J]. Energy, 2014, 64(1): 953-960.

[14] 李刚, 谢永成, 李光升, 等. 基于自适应神经网络模糊推理系统的蓄电池SOH预测[J].微型机与应用, 2011, 30(22): 82-87. Li Gang,Xie Yongcheng, Li Guangsheng, et al. Prediction of Battery SOH Based on Adaptive Neural Fuzzy Inference System[J]. Microcomputer & Its Applications, 2011, 30(22): 82-87.

[15] 张承慧, 李珂, 崔纳新, 等. 混合动力电动汽车能量及驱动系统的关键控制问题研究进展[J].山东大学学报(工学版), 2011, 41(5): 1-8. Zhang Chenhui, Li Ke, Cui Naxin, et al. Research Progress on Key Control Problems Arising from the Energy and Driving System of the Hybrid Electric Vehicle[J]. Journal of Shandong University (Engineering Science), 2011, 41(5): 1-8.

[16] Huang Guangbin, Zhu Qinyu, Siew C K. Extreme Learning Machine: theory and Application[J]. Neurocomputing, 2006, 70(1/3): 489-501.

[17] Hu Xiaosong, Jiang Jiuchun, Cao Dongpu,et al.Battery Healthy Prognosis for Electric Vehicles Using Sample Entropy and Spare Bayesian Predictive Modeling[J]. IEEE Transactions on Industrial Electronics, 2015, 63(4): 2645-2656.

[18] 陈雄姿，于劲松，唐荻音，等. 基于贝叶斯LS-SVR的锂电池剩余寿命概率性预测[J].航空学报，2013, 34(9): 2219-2229. Chen Xiongzi, Yu Jinsong, Tang Diying, et al. Probabilistic Residual Life Prediction of Lithium-ion Batteries Based on Bayesian LS-SVR[J]. Acta Aeronautica et Astronautica Sinica, 2013, 34(9): 2219-2229.

[19] Zhao Qi, Heiinz W, Christian B.Nonlinear Estimation of Li-ion Polymer Battery SOC with Bayesian Filtering[J]. Journal of University of Science and Technology of China, 2012, 42(8): 628-639.

[20] Huang G B, Siew C K. Extreme Learning Machine: RBF Network Case[C]//Proceedings of the Eighth International Conference on Control, Automation, Robotics and Vision. Kunming,2004: 1029-1036.

[21] 何群，李磊，江国乾，等.基于PCA和多变量极限学习机的轴承剩余寿命预测[J].中国机械工程，2014,25(7): 984-989. He Qun,Li Lei,Jiang Guoqian, et al.Residual Life Predictions for Bearings Based on PCA and MELM[J].China Mechanical Engineering,2014, 25(7): 984-989.

[22] Congdon P.Bayesian Statistical Modelling[M]. New York: Wiley, 2006.

[23] Bishop C. Pattern Recognition and Machine Learning[M].New York: Springer-Verlag, 2006.

[24] Chen T, Martin E. Bayesian Linear Regression and Variable Selection for Spectroscopic Calibration[J]. Analytica Chimica Acta,2009,631(1):13-21.

[25] Park H S, Kim C E, Kim C H,et al. A Modularized Charge Equalizer for an HEV Lithium-ion Battery String[J]. IEEE Trans. Ind. Electron, 2009, 56(5): 1464-1476.

(编辑 陈 勇)

Prediction of Internal States of Battery in HEV by BELM

Wang Qi1Sun Yukun2Ni Fuyin1Chen Taihong1Chen Lianyu1Luo Yinsheng1

1.Jiangsu University of Technology,Changzhou,Jiangsu,213001 2.Nanjing Institute of Technology,Nanjing,211167

BELM was proposed based on approach to predict the battery’s internal states of HEVs. The basic principles of BELM were described in detail, and the performance parameters of battery were collected under advanced vehicle simulator(ADVISOR) including voltages, currents, temperatures and so on. Then the BELM was used in the predictions of SOC and SOH, at the same time, the influences of aging battery were taken into account. The results of BELM indicate that the prediction model possesses higher prediction accuracy, and achieves real-time and accurate SOC and SOH predictions with high effectiveness.

Bayesian extreme learning machine(BELM); hybrid electric vehicle(HEV); state of charge(SOC); state of health(SOH)

2016-01-07

TM912

10.3969/j.issn.1004-132X.2016.22.023

王 琪，男，1987年生。江苏理工学院电气信息工程学院讲师、博士。主要研究方向为混合动力汽车复合电源能量管理系统。发表论文20余篇。孙玉坤，男，1958年生。南京工程学院电力工程学院院长、教授、博士研究生导师。倪福银，男，1978年生。江苏理工学院电气信息工程学院讲师、博士研究生。陈泰洪，男，1972年生。江苏理工学院电气信息工程学院高级实验师。陈连玉，男，1970年生。江苏理工学院电气信息工程学院副教授。罗印升，男，1965年生。江苏理工学院电气信息工程学院院长、教授、博士。