基于总体平均经验模式分解近似熵和混合PSO-BP算法的轴承故障诊断方法

张淑清 黄文静 胡永涛 宿新爽 陆 超 姜万录

燕山大学河北省测试计量技术及仪器重点实验室，秦皇岛，066004



基于总体平均经验模式分解近似熵和混合PSO-BP算法的轴承故障诊断方法

张淑清 黄文静 胡永涛 宿新爽 陆 超 姜万录

燕山大学河北省测试计量技术及仪器重点实验室，秦皇岛，066004

针对机械系统的非平稳、非线性特性，提出了一种基于总体平均经验模式分解(EEMD)近似熵和混合PSO-BP算法的轴承故障诊断方法。EEMD能够解决EMD的端点效应，改善处理非线性信号时的局限性；引入随机权重和压缩因子来改进粒子群算法，优化BP神经网络的权值和阈值，解决BP网络的全局收敛问题。将信号经EEMD得到的IMF分量与近似熵结合，组成特征向量，再将构造的特征向量输入到PSO-BP神经网络中进行模式识别。实验及工程应用实例证明了该方法的有效性和优越性。

轴承；故障诊断；总体平均经验模式分解；近似熵；混合粒子群神经网络

0 引言

特征提取和模式识别是机械故障诊断的关键问题。目前常用的处理方法自适应性，在处理非线性、非平稳振动信号时存在局限性[1]。经验模式分解(empirical mode of decomposition，EMD)可以根据振动信号自身的时间特征尺度进行自适应分解，有效处理非线性振动信号[2-3]。但EMD存在端点效应、模态混叠、分解停止准则等问题，使分解结果不理想[4]。总体平均经验模式分解(ensemble empirical mode of decomposition，EEMD)将高斯白噪声信号叠加到原始信号之后进行多次EMD，把多次分解后的IMF分量的均值作为最终结果，可以有效抑制端点效应。EEMD可以保留更多频率和包络信息，因此比EMD优越。近似熵能够显示不同频带内信号的复杂程度，为提取故障信号的特征向量提供了良好依据[5]。

神经网络因其良好的自学习性、并行性及较强的容错能力，被很多学者应用于故障诊断领域[6-7]，但收敛性问题一直制约着其发展。粒子群优化 (particle swarm optimization，PSO) 算法是一种新的基于群体智能的优化算法，通过迭代搜索最优解。PSO算法结构简单，只需根据当前最优解来寻找全局最优解，是解决全局收敛问题的有效途径[8]。PSO算法参数中，惯性权重w是重要的参数，较大的w有利于跳出局部极小值，较小的w有利于精确局部搜索。为解决这一矛盾，本文采用随机权重法克服线性权重的不足，并在PSO算法中引入压缩因子来控制粒子速度。利用改进后的混合PSO算法优化BP神经网络的权值和阈值，可以帮助BP神经网络快速收敛到全局最优点。

1 EEMD近似熵特征提取

EEMD将白噪声信号叠加到原始信号后进行多次EMD[9],得到一组IMF分量。设xn,r为第n(n=1，2，…，N；N为运算次数)次EMD的第r个IMF分量，则可得到N组IMF分量序列{x1,r，x2,r，…，xN,r}，将N组IMF分量序列分量的平均值作为EEMD的第i个IMF分量：

(1)

利用EEMD算法将原始振动信号分解为有限个IMF分量，选取包含故障有用信息的IMF分量，计算其近似熵作为特征向量。

对序列{x(i)|i=1，2，…，N}求取近似熵的步骤如下：

(1)选定嵌入维数m，构造m维向量：

X(i)=(x(i)，x(i+1)，…，x(i+m-1))

(2)

i=1，2，…，N-m+1

(2)将向量X(i)与X(j)对应元素的最大差值定义为两者之间的距离：

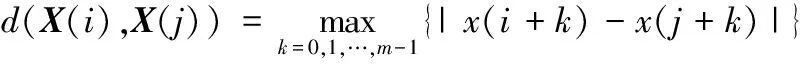
(3)

i,j=1，2，…，N-m+1 且i≠j

(3)设定相似容限的阈值ε，并统计向量X(i)与X(j)距离d(X(i)，X(j))小于ε的数目B{d(X(i)，X(j))< ε}，将其与向量总数N-m+1的比值记为

(4)

(4)Φm(ε)为矢量X(i)的自相关程度，它是所有Cmi(ε)的对数平均值：

(5)

(5) 增加维数构成一组m+1维矢量，重复上述步骤，得到Φm+1(ε)。

(6)当数据长度N为有限值时，按照上述步骤得出时间序列近似熵的估计值：

ApEn(m,ε,N)=Φm(ε)-Φm+1(ε)

(6)

近似熵的取值与相似容限ε和嵌入维数m密切相关。为了得到较好的统计特性，数据长度N通常在100～5000内取值，嵌入维数m一般取1或2，相似容限ε取0.1～0.25倍的序列标准差[10]。

2 混合粒子群神经网络模式识别

2.1 粒子群算法

PSO算法初始时随机产生一个种群，设定每个粒子初始的随机位置和速度。设搜索空间为D维，种群包括K个粒子，种群记为y=(y1，y2，…，yK)，则粒子u(u=1，2，…，K)的位置由yu=(yu1,yu2,…,yuD)表示，粒子u的速度由vu=(vu1,vu2,…,vuD)表示。粒子u到当前时刻为止搜索到的最优位置pud=(pu1,pu2,…,puD)，到当前时刻为止整个粒子群搜索到的最优位置pgd=(pg1,pg2,…,pgD)。搜索到pud和pgd后，粒子通过下式进行速度和位置更新：

vud(t+1)=wvud(t)+c1e1(pud-yud(t))+

c2e2(pgd-yud(t))

(7)

yud(t+1)=yud(t)+vud(t+1)

(8)

式中，w为惯性权重；t为迭代次数；c1、c2为学习因子，起调节作用；e1、e2为0到1之间的随机数；yud、viu分别为粒子u的当前位置和速度。

传统的粒子群算法中，学习因子c1、c2及惯性权重w为常数。

2.2 改进的混合粒子群算法

惯性权重w是PSO算法的重要参数，很多学者采用线性递减权重算法，线性递减权重中较大的w有利于跳出局部极小值，较小的w有利于精确局部搜索，但线性递减惯性权重存在下述问题：如果粒子群在运行初期探测到最优点，则希望能迅速收敛于最优点，但w的线性递减减缓了算法的收敛速度；算法运行后期，随着w的减小，全局搜索能力下降，多样性减弱，容易陷入局部最优[11]。为解决这一问题，本文采用随机权重法克服线性权重的不足，在运算初期接近最优点时，随机权重可以产生较小的w，提高收敛速度；在算法运行后期，随机权重不会线性递减使全局搜索能力下降，可以有效改善全局搜索能力。设w为服从标准正态分布的随机数：

w=μ+σN(0，1)

(9)

μ=μmin+(μmax-μmin)R(0，1)

式中，N(0，1)为标准正态分布的随机数；σ为随机权重平均值的方差，μmax、μmin分别为随机权重平均数的最大值和最小值；R(0，1)为0到1之间的随机数。

为了更好地改进PSO算法模型，笔者引入压缩因子λ来控制粒子的飞行速度，使算法达到全局探测和局部开采的有效平衡[12]。引入压缩因子λ后的粒子速度更新公式为

vud(t+1)=λ[vud(t)+c1e1(pud-yud(t))+

c2e2(pgd-yud(t))]

(10)

(11)

C=c1+c2

本文将随机权重和压缩因子结合，构成了一种新的混合PSO算法。该混合算法既可以通过随机权重有效弥补线性递减权重的不足，又可以通过压缩因子有效控制粒子的飞行速度。新的混合PSO算法粒子通过下式进行速度和位置更新：

(12)

2.3 混合粒子群神经网络模式识别

本文采用3层神经网络优化模型，其网络拓扑结构如图1所示。

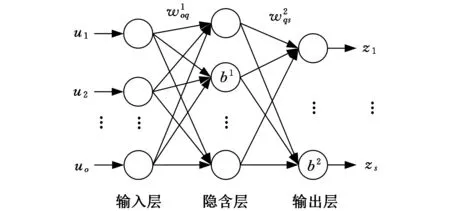
图1 BP神经网络结构图

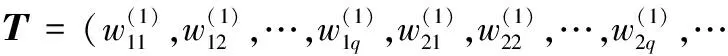
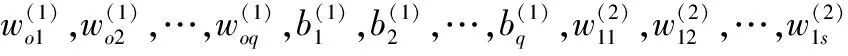
(13)

式中，U为训练样本数；αlj为网络实际输出；βlj为网络期望输出。

式(13)表明，误差越小，粒子寻优性能越好，即粒子在适应度函数最小时寻出BP神经网络的最优权值和阈值，实现对BP神经网络的优化。

混合粒子群优化神经网络的步骤如下：

(1)载入样本数据，初始化化神经网络，确定神经网络的输入层、隐含层和输出层的节点数。

(2)初始化粒子群，确定粒子个数；设定粒子初始位置和速度；设置学习因子c1、c2；设置随机惯性权重平均值的方差σ，随机权重平均数的最大值μmax和最小值μmin。

(3)计算适应度值，BP神经网络的均方误差指标为适应度函数。

(4)根据式(13)适应度值计算当前各粒子的最优位置与总最优位置。

(5)根据式(12)更新粒子速度和位置。

(6) 检查是否达到终止条件，迭代次数达到给定的最大次数或达到最小误差要求时终止，输出优化后神经网络的权值和阈值，否则返回步骤(3)。

3 故障仿真实验

本实验采用美国凯斯西储大学的滚动轴承故障数据[13]。测试轴承为深沟球轴承的驱动端轴承，型号为SKF6205。

3.1 不同类型故障诊断

对轴承正常、滚动体故障、内圈故障、外圈故障4种信号进行分析，轴承转速为1797 r/min，采样频率为12 kHz，每个数据样本长度取1024，图2为4种信号的局部图。

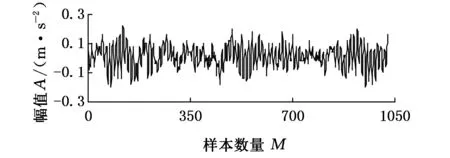
(a)正常

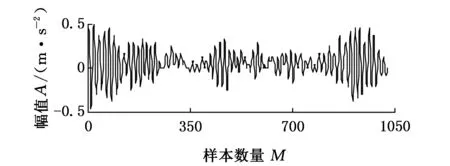
(b)滚动体故障

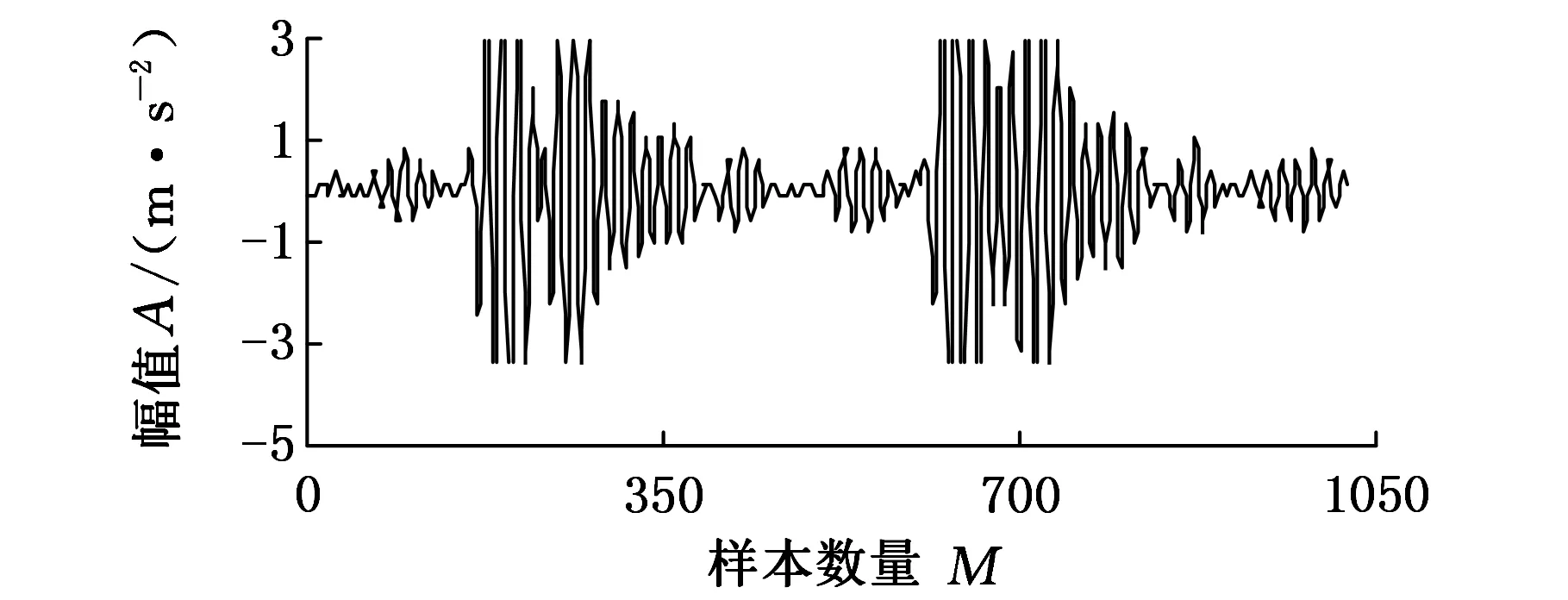
(d)外圈故事图2 轴承4种信号局部图

对4种信号进行EEMD。以轴承内圈故障信号为例，其分解结果如图3所示，内圈信号被分解为9个IMF分量和残余分量r。

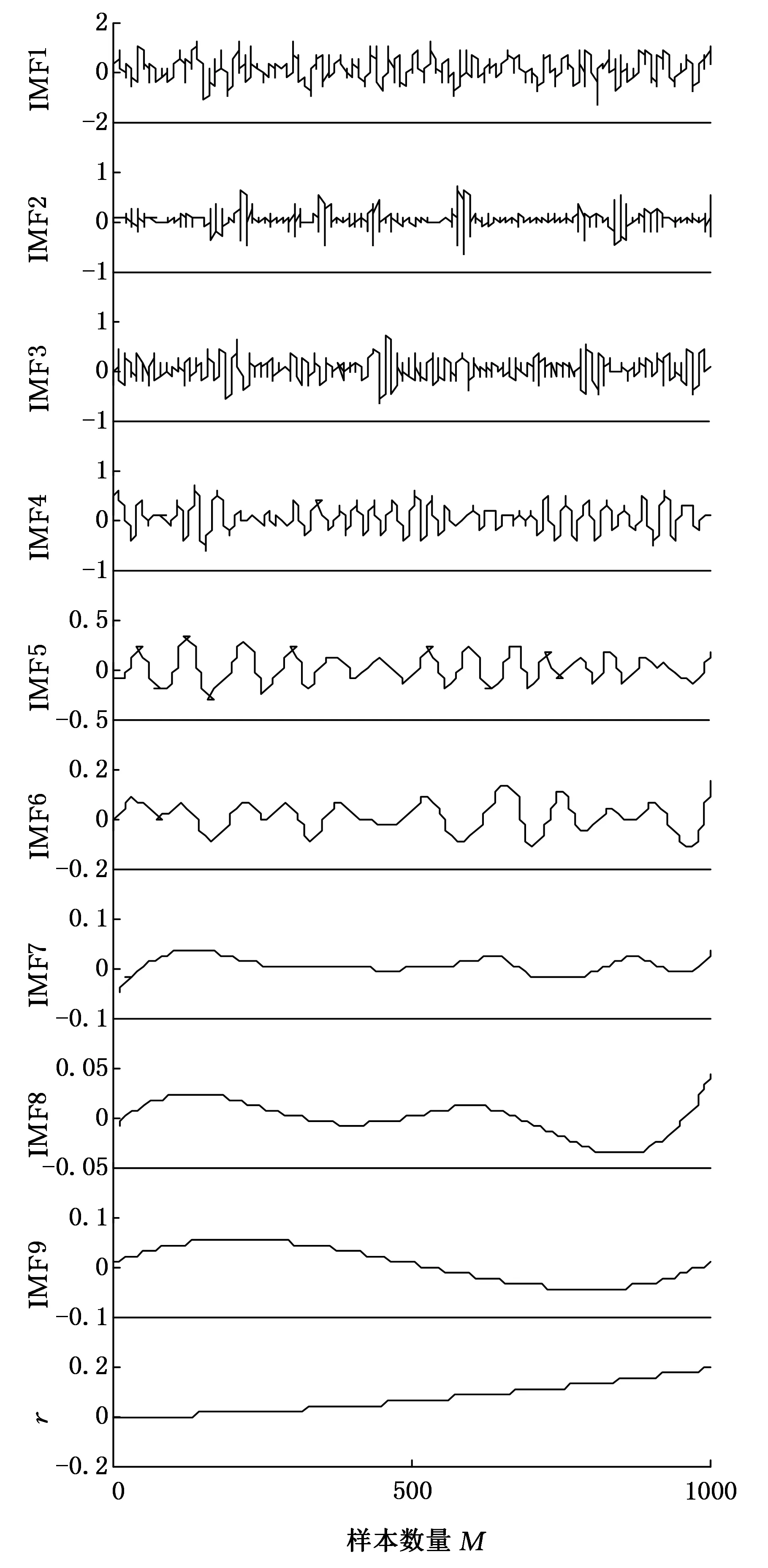
图3 轴承内圈故障信号EEMD图

EEMD后要筛选出与原始信号相关的分量。设{xi} (i=1，2，…，n；n为分量的个数)表示信号分解后的IMF分量。计算各个IMF分量的信息熵H(xi)：

式中，hi为xi取值的概率。

设定阈值γ：

γ=[max(H(xi))-min(H(xi))]/n

(14)

若某一分量的H(xi)≥γ，则该分量包含了原始信号的有用信息，可作为被筛选出的特征量计算近似熵，否则不再考虑该分量。将筛选后m个分量的近似熵作为特征向量。

经过EEMD后，正常、内圈故障和外圈故障信号均被分成了9个IMF分量(IMF1～IMF9)和残余分量，滚动体故障信号被分解为7个IMF分量和残余分量。根据信息熵的特征筛选方法，正常、内圈故障、外圈故障这3种信号EEMD分解后，得到9个IMF分量IMF分量IMF1～IMF4满足前文所述的筛选条件，滚动体故障信号的分量IMF1～IMF3满足筛选条件，综合考虑，将4种信号的前4个分量作为分析对象。4种信号分解，每个分解得到的前4个分量求取近似熵值如表1所示。从表1可得，不同信号的IMF分量近似熵存在一定的区别，说明不同信号不同尺度的复杂度不同。

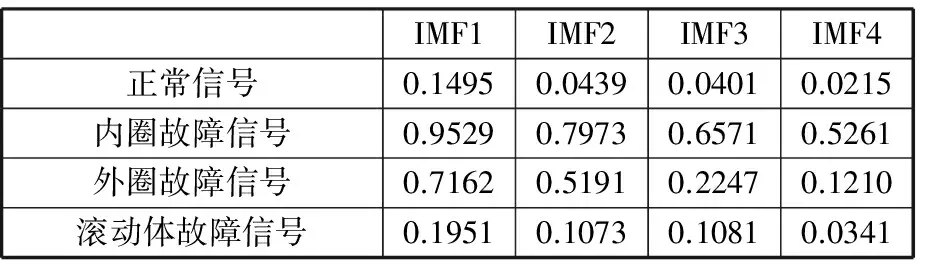
表1 4种信号近似熵值

对4种信号分别取25组数据，共组成100组数据，按照前文所述，分别进行EEMD，计算前4个IMF分量的近似熵，得到100×4的近似熵数据矩阵。对近似熵数据矩阵，每种信号抽取前20组作为样本数据，其余5组为测试数据。测试数据如表2所示，由于篇幅有限，每种测试数据只列出2组。

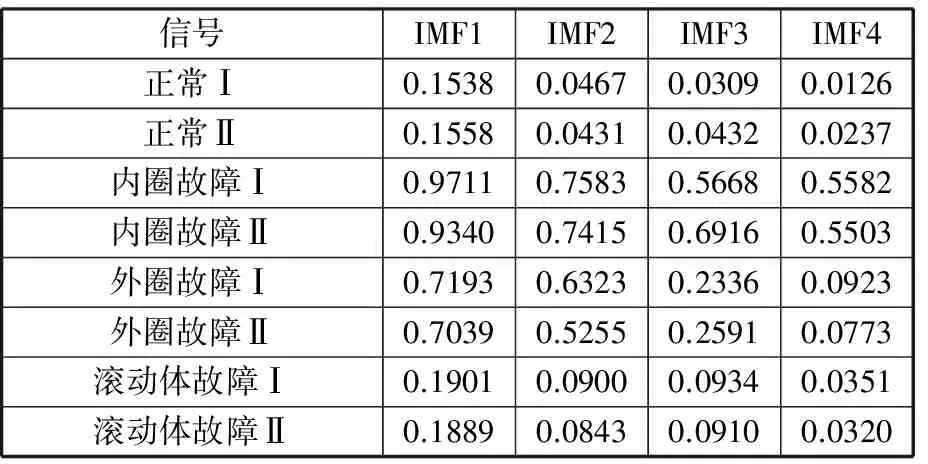
表2 不同类型故障部分测试数据(近似熵)

为了证明改进PSO神经网络的优越性，首先利用BP算法训练神经网络。设BP神经网络输出层节点数为4，网络的期望输出中，(1,0,0,0)代表正常工作，(0,1,0,0)代表内圈故障，(0,0,1,0)代表外圈故障，(0,0,0,1)代表滚动体故障。通过试错法确定隐含层神经元个数为12。设网络收敛目标为10-7，隐含层、输出层的激发函数分别为函数tansig和函数logsig。实验过程中，经过153次迭代后得到输出结果。

然后利用粒子群算法优化神经网络的权值和阈值，设学习因子c1=c2=2.05；设置随机惯性权重平均值的方差σ=0.2，随机权重平均数的最大值μmax=0.9和最小值μmin=0.3。经过29次迭代后得到输出结果。

BP神经网络和粒子群优化神经网络的输出结果如表3所示，和网络的期望输出相比，使用粒子群优化后的神经网络输出结果更接近于期望输出，准确率较高。误差变化对如图4所示。从图4可得，粒子群优化的BP神经网络可以更快收敛，迭代步数较少。

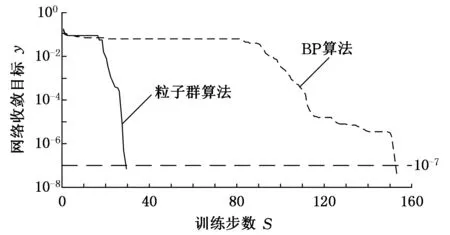
图4 BP算法和粒子群算法对比图

3.2 不同损伤程度故障诊断

对不同损伤程度的内圈信号(正常工作、内圈轻微损伤和内圈严重损伤)进行实验验证，其中，内圈轻微故障的损伤直径为0.1778 mm，内圈严重故障的损伤直径为0.5334 mm。

经过EEMD后，正常、内圈轻微损伤和严重损伤信号均被分成了9个分量(IMF1～IMF9)和残余分量。依据信息熵的特征筛选方法，正常、内圈轻微损伤和严重损伤等3种信号均筛选出的分量IMF1～IMF4满足筛选条件，将3种信号的前4个IMF分量作为分析对象，计算前4个IMF分量的近似熵。设BP神经网络输出层节点数为3，网络的期望输出中， (1,0,0)代表正常工作，(0,1,0)代表内圈轻微故障，(0,0,1)代表内圈严重故障。每种状态提取25组振动信号，共75组进行特征提取。每种特征向量抽取前20组作为样本数据，其余为测试数据。测试数据和输出结果如表4所示，由于篇幅有限，每种测试数据只列出两组。

使用改进的粒子群神经网络算法进行故障诊断，经过17次迭代后得到输出结果，网络误差变化如图5所示。

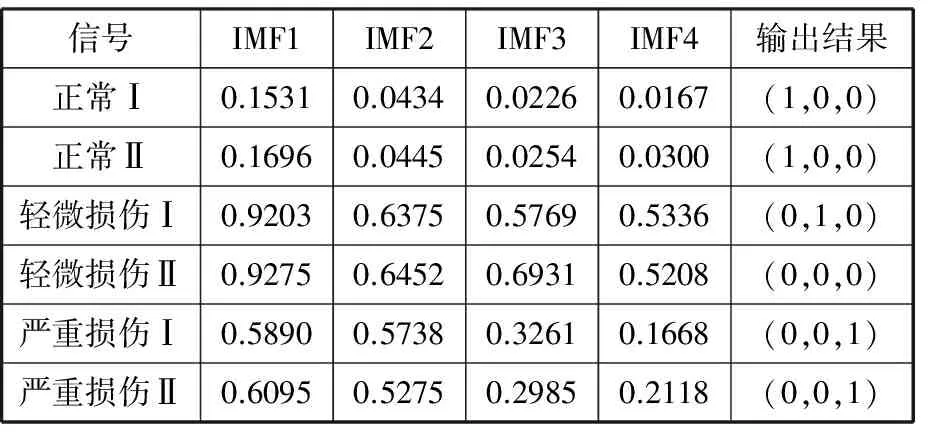
表4 不同损伤程度部分测试数据(近似熵)和输出结果

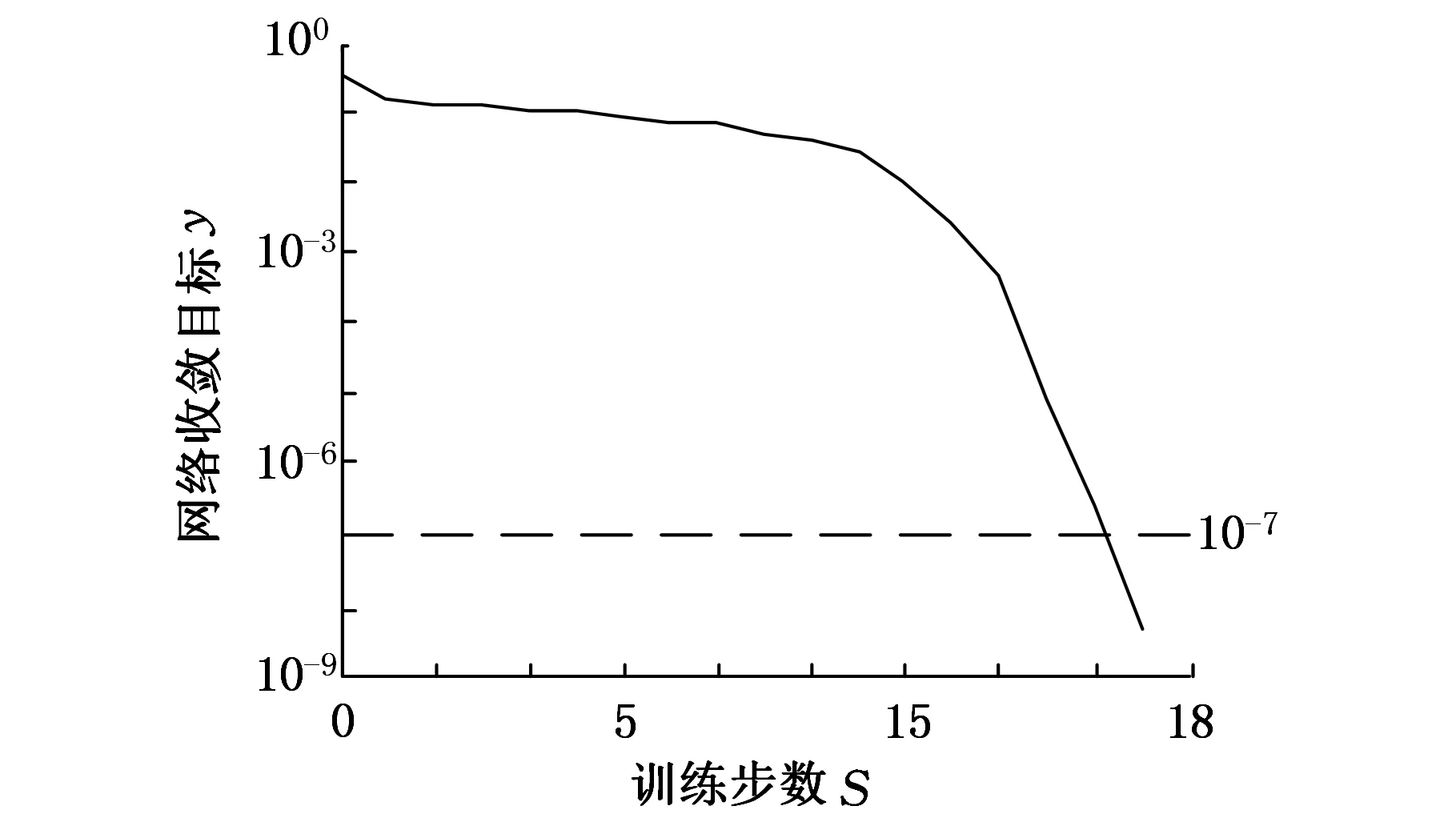
图5 粒子群算法收敛图

4 工程实例分析

对上海宝钢热轧1580SP定宽侧压轧机的动力传输装置——齿轮减速机中的轴承进行分析和诊断。该齿轮减速箱装有2对伞齿轮、4对斜齿轮、1根主轴、3对齿轮轴。主轴发动机入口处安装1个轴承(编号1)、靠近伞齿轮处安装1个轴承(编号2)、每个齿轮轴上分别有1个轴承(编号3～5)[14]。对这5个轴承进行故障识别，图6为该系统简图。

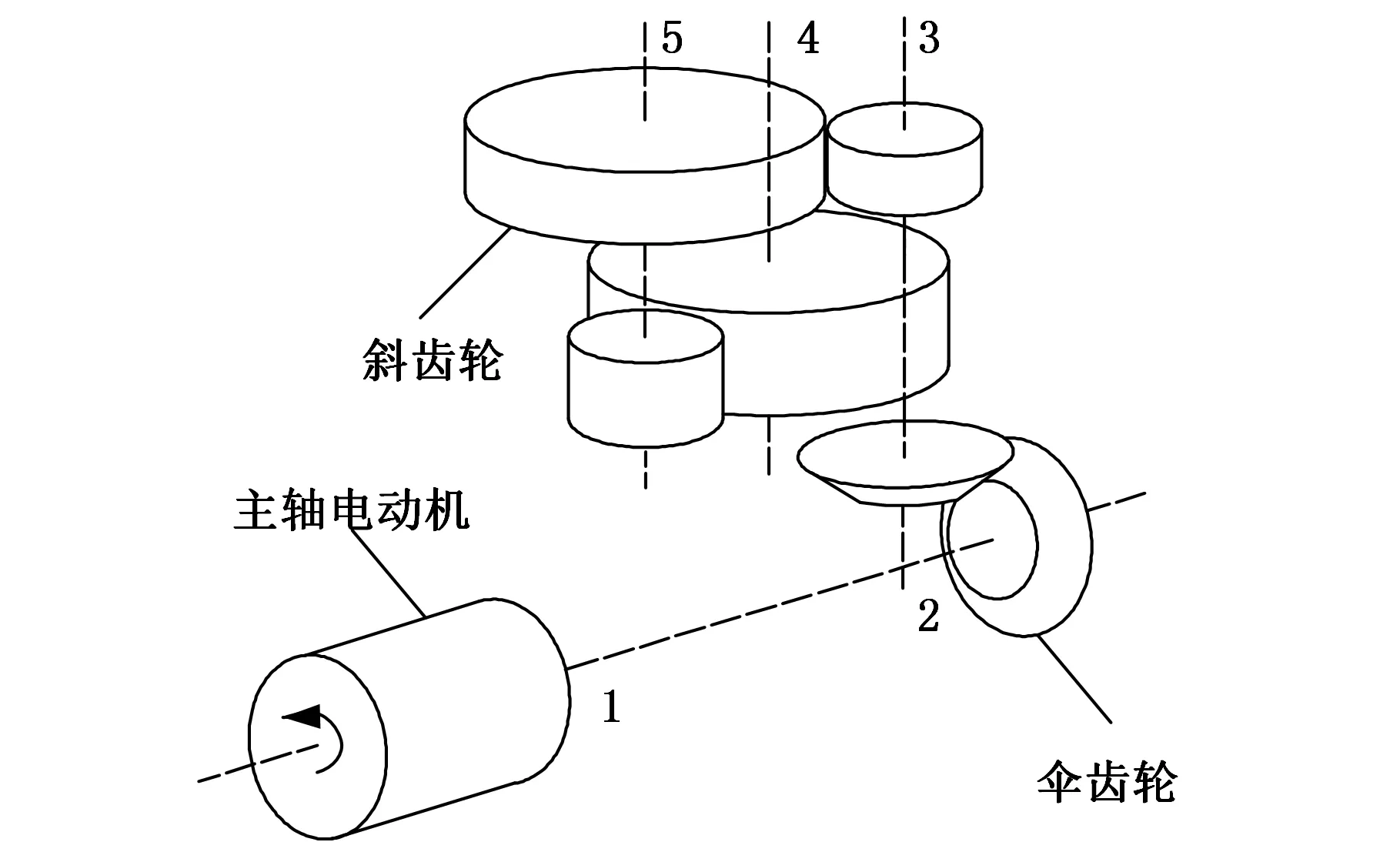
图6 1580SP定宽侧轧机系统简图

正常工作情况下，通过安装在轴承端的集成压电式加速度计对运行状态进行监测，用DASP数据采集仪收集轴承工作时的振动加速度信号。

在轴承测点各采集30组故障信号进行模式识别。首先对振动信号的每组样本进行EEMD，再利用信息熵筛选出与原始信号相关的IMF分量，得出分量IMF1、IMF2、IMF4，计算近似熵，用来构造特征向量，将前15组数据作为样本数据，其余为测试数据。最后用改进的混合粒子群神经网络对该特征矩阵进行故障识别。识别结果如表4所示。可以看出，在排除外界因素对信号的影响后，5个轴承测点的识别率都很高，本方法处理后得到了很好的结果。

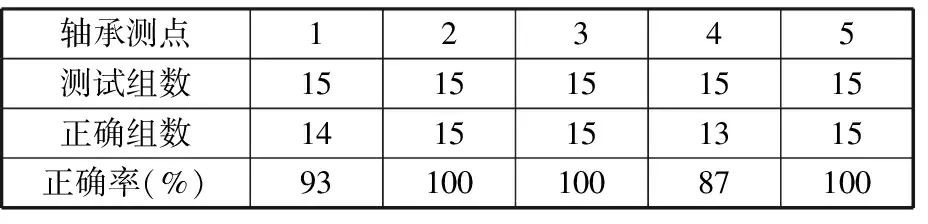
表4 识别结果

5 结论

(1) EEMD可以抑制EMD端点效应的问题，近似熵可以揭示信号在不同尺度的复杂程度，将二者结合的方法为机械故障的特征提取提供了一种新的有效方法。

(2)改进的混合粒子群算法可以有效弥补BP神经网络难以快速收敛到全局最优解的不足，EEMD近似熵和混合粒子群神经网络的故障诊断方法具有结构简单、收敛速度快、识别能力强的优点。实验结果和工程实例分析表明，该方法可以很好地实现对滚动轴承的状态检测及故障诊断。

[1] 王太勇，何慧龙，王国锋，等. 基于经验模式分解和最小二乘支持矢量机的滚动轴承故障诊断[J]. 机械工程学报，2007，43(4)：88-92. Wang Taiyong，He Huilong，Wang Guofeng，et al. Rolling Bearings Fault Diagnosis Based on Empirical Mode Decomposition and Least Square Support Vector Machine[J]. Journal of Mechanical Engineering，2007，43(4)：88-92.

[2] 孟宗，李珊珊. 基于小波半软阈值和EMD的旋转机械故障诊断[J]. 中国机械工程，2013，24(10)：1279-1283. Meng Zong，Li Shanshan. Research on Fault Diagnosis for Rotating Machinery Based on Semi-soft Wavelet Threshold and EMD[J]. China Mechanical Engineering，2013，24(10)：1279-1283.

[3] 吴虎胜，吕建新，吴庐山，等. 基于EMD和SVM的柴油机气阀机构故障诊断[J]. 中国机械工程，2010，21(22)：2710-2714. Wu Husheng，Lü Jianxin，Wu Lushan，et al. Fault Diagnosis for Diesel Valve Train Based on SVM and EMD[J]. China Mechanical Engineering，2010，21(22)：2710-2714.

[4] 时培明，李庚，韩东颖. 基于改进EMD的旋转机械耦合故障诊断方法研究[J]. 中国机械工程，2013，24(17)：2367-2372. Shi Peiming，Li Geng，Han Dongying. Study on Coupling Faults of Rotary Machinery Diagnosis Method Based on Improved EMD[J]. China Mechanical Engineering，2013，24(17)：2367-2372.

[5] Danlel P C，Jose A R. Identification of Dynamic Instabilities in Machining Process Using the Approximate Entropy Method[J]. International Journal of Machine Tool & Manufacture，2011，51：556-564.

[6] 李胜，张培林，李兵，等. 量子BP神经网络在发动机故障诊断中的应用[J]. 中国机械工程，2014，25(16)：2159-2163. Li Sheng，Zhang Peilin，Li Bing，et al. Application of Quantum BP Neural Network in Engine Fault Diagnosis[J]. China Mechanical Engineering，2014，25(16)：2159-2163.

[7] 叶瑞召，李万红. 基于小波包分解和 BP 神经网络的轴承故障诊断[J]. 轴承，2012 (10)：53-56. Ye Ruizhao，Li Wanhong. Fault Diagnosis for Bearings Based on Wavelet Packet Decomposition and BP Neural Network[J]. Bearing，2012 (10)：53-56.

[8] 孟栋，樊重俊，吴天魁. 混沌粒子群神经网络在非线性函数拟合中的应用研究[J]. 计算机与应用化学，2014，31(5)：567-570. Meng Dong，Fan Chongjun，Wu Tiankui. Study on the Application of Chaotic Particle Swarm Neural Network in Nonlinear Function Fitting[J]. Computers and Applied Chemistry，2014，31(5): 567-570.

[9] 刘涛，黄其柏. 基于EEMD和HT的轴流泵压力脉动特征信息提取[J]. 机电工程，2012(3)：278-281. Liu Tao，Huang Qibai. Characteristic Information Extraction of Pressure Pulsation Signal in Axis-flow Pump Based on EEMD and HT[J]. Journal of Mechanical & Electrical Engineering，2012(3)：278-281.

[10] 曹彪，吕小青，曾敏，等. 短路过渡电弧焊电流信号的近似熵分析[J]. 物理学报，2006，55(4)：1696-1704. Cao Biao，Lü Xiaoqing，Zeng Min，et al. Approximate Entropy Analysis of Current Signal of Arc Welding Current in Short Circuit[J]. Acta Physica Sinica，55(4)：1696-1704.

[11] 魏秀业，潘宏侠. 粒子群优化及智能故障诊断[M]. 北京：国防工业出版社，2010.

[12] Kennedy J. Particle Swarm Optimization[M]. New York：Springer，2010.

[13] The Case Western Reserve University Bearing Data Center Website. Bearing Data Center Seeded Fault Test Data[EB/OL]. [2007-11-27]. http:∥www.eecs.case.edu/laboratory/ bearing/download.htm.

[14] 张淑清，张金敏，赵玉春，等. 基于混沌与模糊聚类的机械故障自动识别[J]. 机械工程学报，2011，47(19)：81-85.Zhang Shuqing，Zhang Jinmin，Zhao Yuchun，et al. Research on Automatic Diagnosis Techniques of Machinery Fault Based on Chaos and Fuzzy Clustering Analysis[J]. Journal of Mechanical Engineering，2011，47(19)：81-85.

(编辑 张 洋)

Bearing Fault Diagnosis Method Based on EEMD Approximate Entropy and Hybrid PSO-BP Algorithm

Zhang Shuqing Huang Wenjing Hu Yongtao Su Xinshuang Lu Chao Jiang Wanlu

Measurement Technology and Instrumentation Key Lab of Hebei Province，Yanshan University，Qinhuangdao，Hebei，066004

According to the non-stationary and nonlinear characteristics of mechanical faults, a new method for bearing fault diagnosis was put forward based on EEMD approximate entropy and hybrid PSO-BP algorithm. EEMD might resolve the end effects of the EMD, improving the limitations of EMD when dealing with nonlinear signals; the random weights and the compression factors were introduced to improve particle swarm optimization(PSO) algorithm so as to optimize BP neural network, realizing fast convergence to optimal solution effectively of neural network. Signals were first decomposed by EEMD to get the instrinsic mode function(IMF) components, and to construct feature vectors together with the approximate entropy and the constructed feature vectors were put into the PSO-BP neural network for pattern recognition. The experiments and the engineering tests demonstrate the efficiency and superiority of this method.

bearing; fault diagnosis; ensemble empirical mode decomposition (MEMD); approximate entropy; hybrid particle swarm neural network

2015-03-24

国家自然科学基金资助项目(51475405，61077071)；河北省自然科学基金资助项目(F2015203413)；河北省高等学校科学技术研究重点项目(ZD2014100)

TH17

10.3969/j.issn.1004-132X.2016.22.012

张淑清，女，1966年生。燕山大学电气工程学院教授、博士研究生导师。主要研究方向为弱信号检测、智能信号处理、故障诊断等。发表论文50余篇。黄文静，女，1990年生。燕山大学电气工程学院硕士研究生。胡永涛，男，1987年生。燕山大学电气工程学院博士研究生。宿新爽，女，1991年生。燕山大学电气工程学院硕士研究生。陆 超，男，1991年生。燕山大学电气工程学院硕士研究生。姜万录，男，1964年生。燕山大学机械工程学院教授、博士研究生导师。