不同波长瞬态侧风对汽车气动性能影响分析

黄泰明 谷正气 丰成杰 陈 阵

1.湖南大学汽车车身先进设计制造国家重点实验室，长沙,4100822.湖南理工学院,岳阳,414006 3.湖南文理学院,常德,415000



不同波长瞬态侧风对汽车气动性能影响分析

黄泰明1,2谷正气1,3丰成杰1陈 阵1

1.湖南大学汽车车身先进设计制造国家重点实验室，长沙,4100822.湖南理工学院,岳阳,414006 3.湖南文理学院,常德,415000

利用大涡模拟对某轿车受到的瞬态侧风进行研究，并采用自定义函数(UDF)控制边界的方法实现了正弦侧风在时间及空间上的瞬态变化，分析了三种不同波长的正弦侧风对气动力系数的影响，并将结果与风洞实验及稳态模拟的结果进行对比。结果表明：受到瞬态变化的正弦侧风时，气动力系数呈周期性变化，但气动阻力系数的变化频率是气动侧力及横摆气动力矩系数变化频率的两倍；瞬态正弦侧风波长减小时，气动阻力系数的变化范围逐渐减小；在瞬态侧风作用下，A柱对汽车的气动性能产生了重要影响。

大涡模拟;瞬态侧风;波长;气动力系数

0 引言

在实际环境中，受到气候、周围环境等因素的影响，高速行驶的汽车经常会受到侧向风的影响，使车辆所受到的瞬态气动力发生急剧变化，从而引起车辆行驶特性的改变，使车辆偏离正常的行驶轨迹，甚至引发交通事故[1]。因此，为了保证行车安全, 研究瞬态侧风对高速行驶车辆气动特性的影响是非常必要的[2]。

有学者采用复杂的风洞实验方法对瞬态侧风的影响进行了研究[3-4]，但利用风洞实验再现汽车遇到侧风的复杂工况是非常困难的。而采用计算流体动力学(computational fluid dynamics,CFD)方法研究瞬态侧风是非常有效的，且能够提供更多的瞬态变化信息，可对实际行驶过程中的汽车气动性能进行更深入研究[5-6]。但是，传统的雷诺平均模拟(RANS)方法并不适用于瞬态的分析，特别是在瞬态侧风或是复杂行驶工况下。Guilmineau[7]的研究表明,采用RANS方法模拟复杂的不稳定流场并不能反映真实的流场，而大涡模拟(large eddy simulation，LES)方法模拟瞬态流场是非常有效的。Cheng等[8]采用LES方法对某轿车尾部流程进行了模拟，模拟结果与实验结果保持了良好的一致性。所以本文采用LES方法对瞬态侧风进行模拟分析。

有很多学者采用CFD方法对侧风进行了研究，如文献[9]采用偏转车身等形式的方法对侧风进行了研究，但该方法无法对时变及空间同时变化的侧风进行研究，且工作量巨大[10]。文献[11]采用动网格的方法对侧风进行研究,由于受到计算资源等的影响，所花费的时间非常长，给研究带来极大的困难。自然界中的侧风变化非常复杂，侧风的方向、波长的变化对流场的影响产生重要影响[12]。用自定义函数(UDF)控制边界条件实现侧风的模拟，它所需要的资源远低于动网格及偏转车身等方法需要的资源，能节省大量的时间，本文采用UDF控制边界的方法实现了瞬态侧风在时间及空间上的变化，并研究了瞬态侧风对流场及气动力系数的影响。

本文采用LES方法对某轿车受到几种不同波长正弦侧风的影响进行了仿真分析，并在风洞中进行了稳态实验，将稳态实验结果与仿真结果进行对比，验证了模拟的准确性。讨论了不同波长的瞬态侧风对气动力的影响，并对车身周围的流场进行了分析。

1 数值计算方法

1.1 模型的建立

建立1∶3的比例模型(图1)，模型尺寸与风洞实验模型尺寸一致。对原始模型进行适当的简化处理，忽略门把手、雨刮器、后视镜支架等，并对底盘做平整化处理。 简化后的模型尺寸如下：车身长、宽、高分别为L=1588 mm，W=643 mm，H=505 mm。

图1 车身简化模型

1.2 计算域及边界条件

数值仿真时采用的计算域为长方形，大小设置如下：入口距车前端5倍车长，出口距车后端7倍车长，总高度为5倍车高，为了保证侧风进入流场后流场的稳定性，计算域两侧距车各10倍车宽(图2)。阻塞比为0.95%，而在进行空气动力学研究时，阻塞比一般不超过5%[13]。

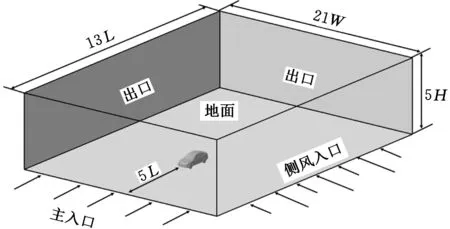
图2 计算域及边界条件

边界条件设置如下：①主入口。Velocity-inlet边界，风速v=27.5 m/s。②侧风入口。采用UDF控制风速及方向。③出口。两个出口都采用Pressure-outlet边界，出口处相对大气压力为0。④地面。Moving-wall边界，自由滑移壁面。⑤顶面及车身表面。Wall边界，无滑移壁面。

1.3 网格划分及网格无关性

采用商用软件ICEM CFD 15.0将计算域生成非结构化网格，由于车身周围存在转捩等复杂现象[14]，为了准确地模拟车身周围的流场，对车身周围需要重点关注的区域的网格进行加密，在本文中采用了5种不同密度的网格(图3)；在车身表面拉伸出平行的三棱柱网格，以满足壁面函数的需求，精确模拟汽车表面的附面层[15]；车尾流场影响主要是在近1.5倍车长区域[16]，故在尾部区域采用了3种不同尺寸的网格，以达到局部网格细化，更多地获取尾部流场数据。

图3 网格拓扑结构及附面层网格

为了进行网格无关性验证，采用与风洞实验一致的方法将车辆横摆20°，在风速为30 m/s的工况下进行稳态仿真计算，并采用了三种不同数量的网格，将结果与风洞实验结果进行对比。网格数量方案分别为9.32×106、1.47×107和2.08×107，其第一层网格中心到壁面的距离y+均小于1。计算所得的阻力系数Cd、升力系数Cl及实验的结果见表1，由表1可知方案二能在保证计算精度的条件下消耗较少的计算资源，因此，本文仿真中采用的网格方案为方案二。

1.4 湍流模型

LES方法的基本思想是：湍流流动由不同尺度的漩涡组成，大尺度的涡旋对湍流能量和雷诺应力的产生以及各种量的湍流扩散起主要作用。大涡的行为强烈地依赖于边界条件，随流动的类型而异。小涡对上述职能的贡献较小，最小的涡主要起耗散作用[17]。在高雷诺数下，小涡近似于各向同性，受边界条件影响较小，具有较大的共同性。虽然目前的计算机还不能计算到耗散尺度，但能够小到惯性区尺度，所以可通过离散时间相关的N-S方程来确定大涡的行为，而用较通用的模型去模拟小涡的作用。这种方法比直接求解RANS方程和DNS方程效率更高，消耗系统资源更少，但却比一般湍流模型方法更精确。

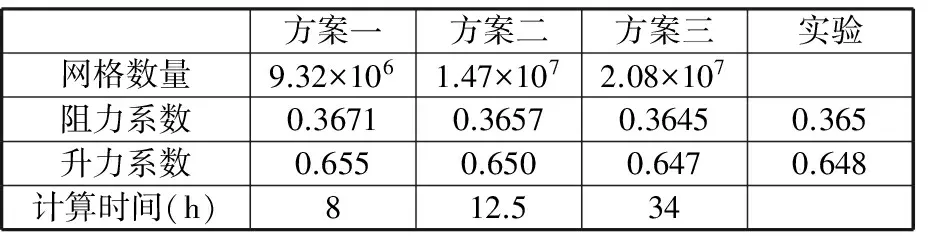
表1 不同数量网格气动力系数对比

(1)

经过滤波后的基于LES 的非定常不可压N-S方程可表示为

(2)

(3)

式中,vSGS为网格运动的涡流黏度。

本文采用Smagorinsky模型，则亚格子湍流黏性可表示为

(4)

1.5 侧风模型

汽车在实际行驶时受间隔的建筑物、路基或路旁的灌木丛等影响，使得汽车受到的侧风呈正弦变化或近似正弦规律变化，所以本文主要研究的侧风为正弦侧风。考虑到自然界侧风受到环境及气候的影响，侧风在空间及时间上是瞬变的，且侧风的大小及方向都是在不断变化的[19]，故本文主要研究三种不同波长的侧风。正弦侧风模型表示为

u=u0sin 2π(X/λ-ft)

其中，u0为侧风的最大风速，本文中侧风风速最大值为10 m/s；λ为侧风的波长，为了使所选取的波长更有代表意义，在本文中取三种波长分别为L、2L和6L，在这三种工况中能更好地观察车身表面压力及周围流程；X为计算域沿X轴方向的坐标；f为侧风变化的频率，由于侧风沿X轴方向运动的速度为主入口的风速v，所以侧风的频率为f=v/λ。图4为本文所模拟正弦侧风示意图。

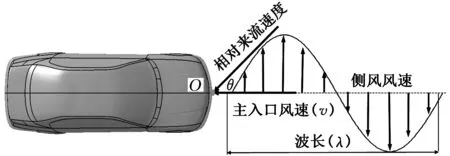
图4 正弦侧风示意图

2 结果分析

2.1 实验验证

对本文湍流模型的准确性进行了验证，因无法获取受瞬态侧风实验数据，故采用与其他学者相似的方法进行验证[20]。在湖南大学HD-2风洞中进行了稳态实验，该风洞高速试验段横截面为矩形，长17 m，宽3 m，高2.5 m，最大风速为58 m/s，收缩比为3.2；风洞速度场的不均匀性小于1%，占截面积的76%以上。其中气动阻力测试采用六分量浮框式应变汽车专用天平。为了保证准确性，实验采用了1∶3的比例模型，与仿真模型一致，风洞实验现场如图5所示。

图5 风洞实验现场

图6为横摆角为20°时Y=0截面速度云图及流线图，在图6a中可以发现车辆纵对称面尾部存在一个自由滞止点的涡A。图6b所示为采用LES模拟稳态侧风的结果，与实验结果基本一致，自由滞止点涡A的形状也基本一致，但与粒子图像测速技术(particle image velocimetry,PIV)实验结果得到的涡的大小、位置有一定的差异；实验时涡A要比仿真时稍大，仿真时涡A在水平方向上离车身更近，而在实验时涡A在竖直方向上离地面更高一些。差异存在的原因主要是实验时环境与数值模拟有一定的差别。这也证明了本文所选取的湍流模型的可靠性。

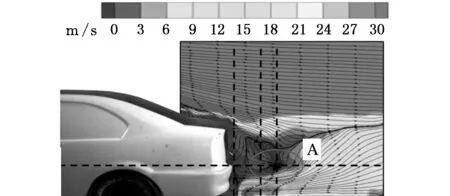
(a)PIV实验

(b)数值模拟图6 纵对称面速度云图及流线图

2.2 不同波长的侧风对气动力系数的影响

本文主要对3种不同波长下的瞬态侧风对气动阻力系数Cd、气动侧力系数Csd及气动横摆力矩系数Cm的影响进行分析。采用大涡模拟时每步的计算气动力系数及流场结果都被保存，如图7～图10所示。

图7 气动阻力、侧力及横摆气动力矩系数曲线(λ=L)

图9 气动阻力、侧力及横摆气动力矩系数曲线(λ=6L)

(a)λ=L

(b)λ=2L

(c)λ=6L图10 Z=70 mm截面上Y方向的速度分布云图

由于本文中的侧风为时间及空间瞬变侧风，无法按常规的稳态侧风方式确定合成侧风的方向，即无法确定车辆横摆角θ，故指定在车辆最前点O点处(图4)的正上方4倍车高处的Y方向风速(侧风风速)与X方向风速(主入口风速)合成的角度为车辆横摆角，则本文中车辆横摆角θ的范围为-20°～20°。

从图7～图9可以发现，随着侧风在时间和空间上发生周期性变化，汽车上所受到的气动力系数也发生周期性变化。侧风的波长发生变化，导致车辆所受到的气动力系数变化的周期也明显不同，侧风波长越小，气动力及横摆气动力矩系数变化的周期越短。还可以发现，随着正弦侧风的波长发生变化，汽车所受到的气动侧力系数以及横摆气动力矩系数的变化幅度发生明显的变化，正弦侧风的波长越长，气动侧力以及横摆气动力矩系数变化幅值越大，而气动阻力系数的变化幅值相对要小一些。

从图10可以发现车身受到波长λ分别为L、2L和6L三种不同正弦侧风作用时，计算域内Y方向速度场也呈现出正弦分布。在车身两侧及尾部流场由于受到车身周围气流迟滞效应的影响[21]，车身周围流场Y方向的速度分布出现不规律变化；离尾部较远处的网格没有加密，导致速度呈正弦分布的趋势减弱。

图11～图13所示为按横摆角变化的单周期内气动力系数的变化迹线，即将图7中的气动力系数曲线用车辆位置变化表示。可以发现：在实验及稳态模拟下，气动力系数相差很小，且基本上都是随着横摆角度的变化而线性变化的；在瞬态正弦侧风作用下变化趋势完全不同。从图11～图13可以发现稳态模拟的气动阻力、侧力及横摆气动力矩系数与风洞实验相差很小，最大误差不超过6%，变化趋势也基本一致，验证了该湍流模型数值计算的可靠性。

1.λ=L 2.λ=2L 3.λ=6L 4.实验 5.稳态仿真图11 气动阻力系数变化迹线

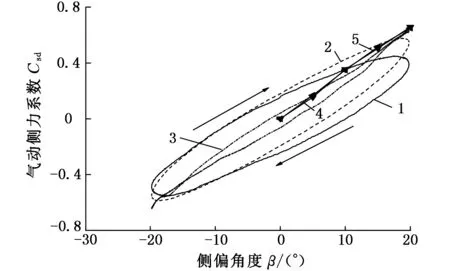
1.λ=L 2.λ=2L 3.λ=6L 4.实验 5.稳态仿真图12 气动侧力系数变化迹线

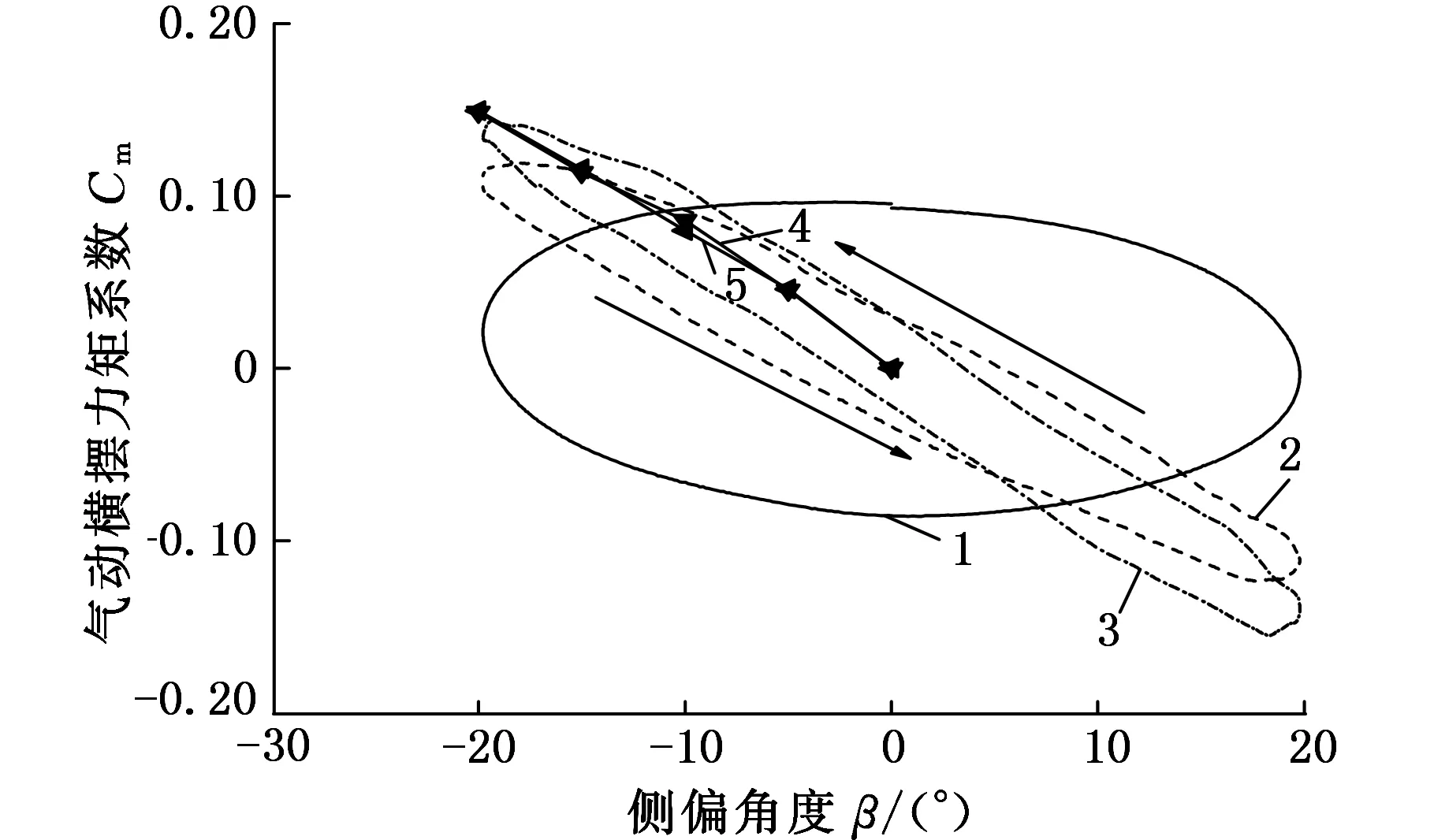
1.λ=L 2.λ=2L 3.λ=6L 4.实验 5.稳态仿真图13 横摆气动力矩系数变化迹线

2.2.1 不同波长的侧风对气动阻力的影响

图11中气动阻力系数的迹线呈现“蝴蝶结”形，可以发现气动阻力系数的变化频率是侧风变化频率的两倍；还可以发现随着侧风波长的逐渐减小，气动阻力系数的变化逐渐变小，波长为L时，最大、最小气动阻力系数分别为0.339和0.284，变化幅度为0.055；波长为6L时，最大、最小气动阻力系数分别为0.353和0.282，变化幅度为0.071，波长为6L时气动阻力系数变化幅值比波长为L时的气动阻力系数变化幅值增大约30%。在稳态仿真时最大、最小气动阻力系数分别为0.3657和0.2847，变化幅值为0.081，稳态模拟时气动阻力系数变化幅值比波长为L时的气动阻力系数变化幅值增大约47%。随着侧风波长的逐渐减小，侧风波长逐渐接近于车长，气动阻力系数的变化范围也越来越小。

对气动阻力产生影响的一个重要因素是尾涡结构[22]，而从图14～图16可以明显发现：在不同波长的侧风影响下尾涡的位置及形状完全不同。这主要是因为侧风的波长越小，在车长范围内气流的速度及方向变化越快，从而导致尾部气流在分离时就被迅速变化的气流所影响，故在图14中无法观察到明显的涡系结构；在图15和图16中由于侧风的波长较长，导致车身周围气流变化速度相对较慢，对尾部气流的分离干涉较小，也就可以观测到明显的涡系结构。

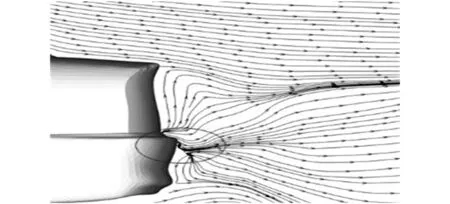
图14 横摆角为20°时Y=0截面尾部的流线图(λ=L)

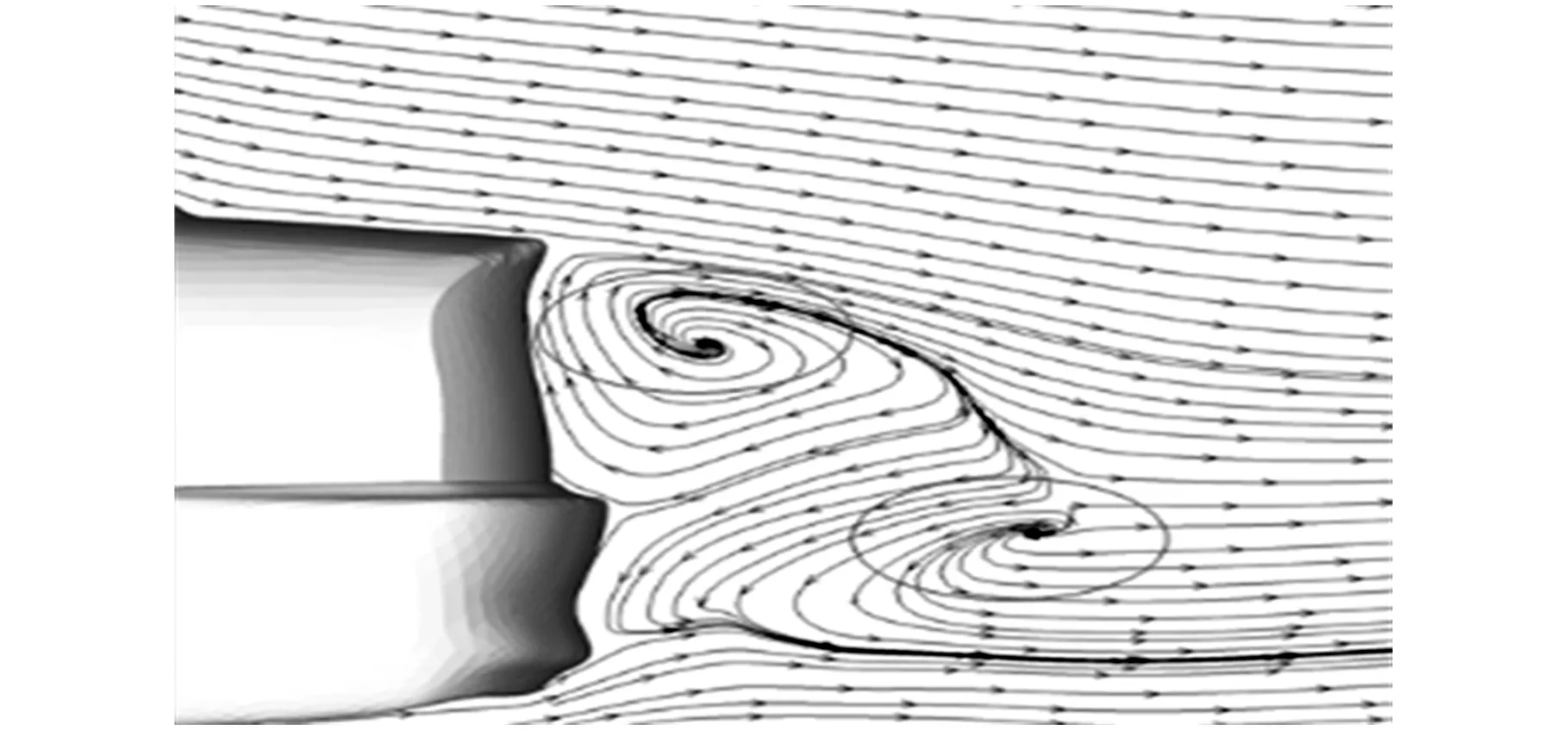
图15 横摆角为20°时Y=0截面尾部的流线图(λ=2L)

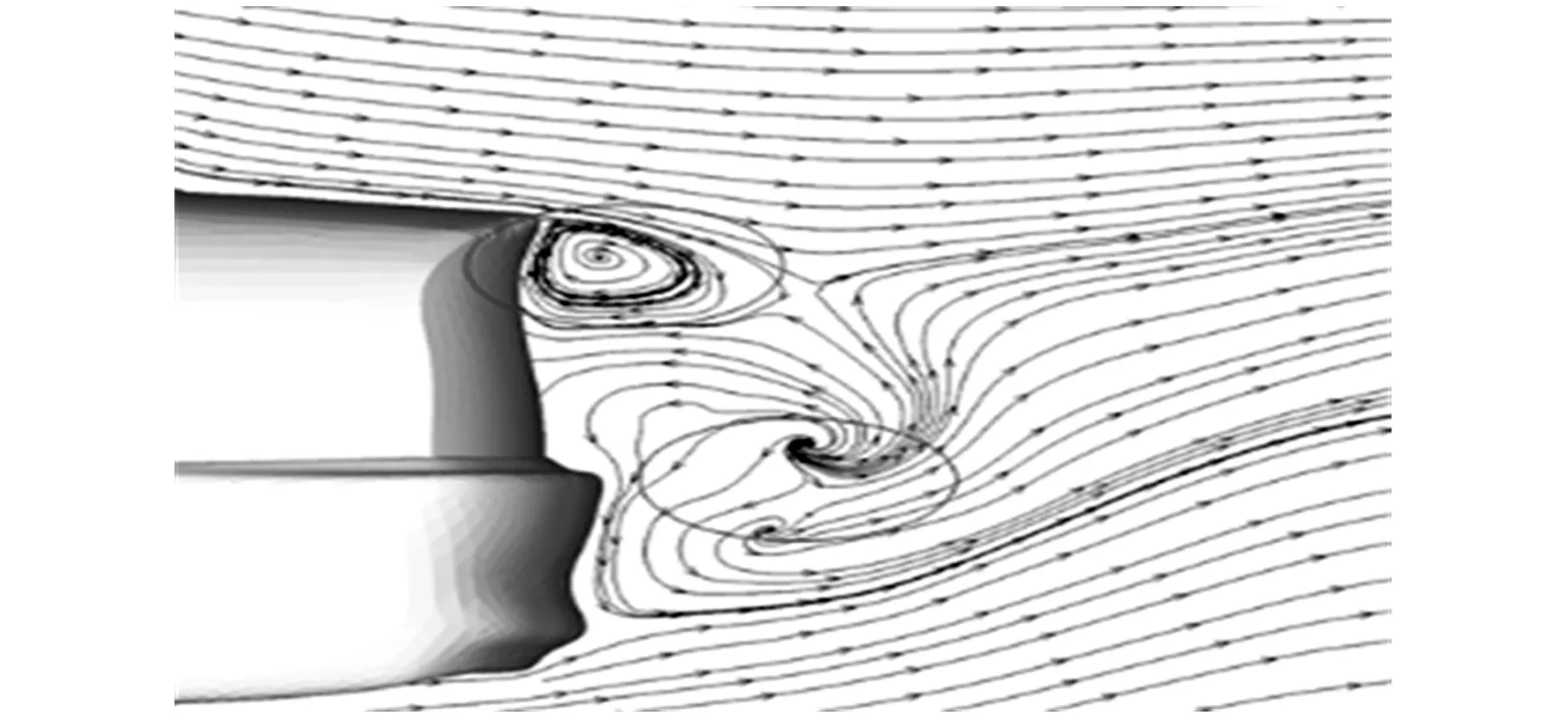
图16 横摆角为20°时Y=0截面尾部的流线图(λ=6L)

2.2.2 不同波长正弦侧风对气动侧力及横摆气动力矩的影响

从图12、图13可以发现气动侧力系数及横摆气动力矩系数变化迹线近似于椭圆形，且呈现出旋转对称性，表示气动侧力系数及横摆气动力矩系数的变化频率与正弦侧风的变化频率一致。椭圆形迹线的宽度反映出在不同波长下气动侧力及横摆气动力矩系数的相位的变化，从图12、图13可以发现，随着波长的减小，气动侧力及横摆气动力矩系数的相位变化更明显。

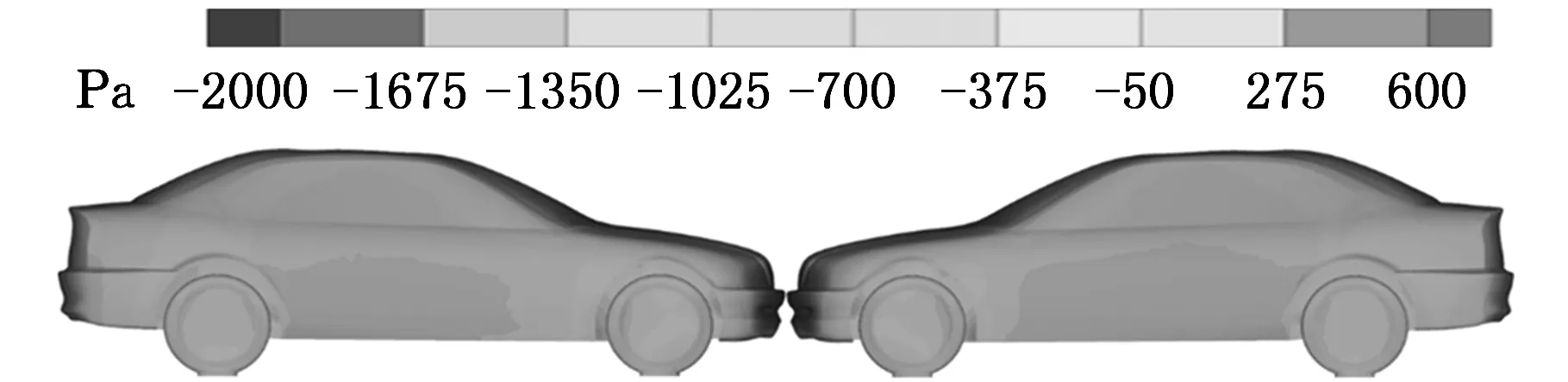
(a)无侧风

(b)有侧风状态(0.8 s时)

(c)有侧风状态(0.82 s时)图17 侧风波长λ=L时车身表面的压力分布

侧风波长变化引起气动侧力及横摆气动力矩系数相位明显变化的主要原因是车身表面所受到Y向压力的变化。从图10可以发现：在不同的波长情况下，车身周围的Y向速度变化很大，从而对车身表面的压力分布产生重要的影响；波长越短，车身表面沿X方向的压力呈现出正负分布的趋势，从而对车身所受到的横摆气动力矩变化产生重要影响。图17所示为侧风波长λ=L时车身表面的压力分布。可以看出：侧风波长为L时，在不同的时刻车身两侧表面的压力分布明显不同，且在图17b与图17c中车身所处的侧风刚好相差1/4个相位，车身左右两侧沿X方向正负压区的位置也明显间隔一段距离，且受瞬态侧风在不同时刻与不受侧风时车身表面的压力分布也存在区别明显。同理，其他时刻及不同波长的正弦侧风在车身两侧表面的压力也会存在相似的变化规律。

从图12可以发现：当侧风的波长增加到6L时，气动侧力系数的迹线所形成的椭圆形的宽度非常小，变化趋势与稳态模拟及实验所得的结果非常相似;当侧风波长为2L及L时，气动侧力系数与稳态仿真结果存在明显的区别。

从图13可发现：横摆气动力矩系数变化趋势与气动侧力系数的变化趋势相似，随着侧风波长的增大，横摆气动力矩系数的相移变小，当侧风波长为L时，横摆气动力矩系数的迹线近似于圆形。而横摆气动力矩系数的迹线与气动阻力及侧力系数迹线存在的最大区别是：侧风波长越小时，横摆气动力矩系数迹线的对称轴接近于水平，而气动阻力及侧力系数迹线的对称轴并不存在此现象。这也说明在瞬态正弦侧风作用下，侧风波长接近车长时，车辆横摆角对横摆气动力矩的影响比车辆横摆角对气动侧力的影响要小一些。

波长不同时车身周围的涡量见图18。可以发现：在不同波长的侧风作用下，车身周围的涡量图有明显的不同，这说明车身周围的气流分离及流动状态明显不同，对车身表面压力及横摆气动力矩产生影响；特别是A柱所形成的拖拽涡在不同波长的侧风作用下长度明显不同，拖拽涡越长影响越大[23]；波长为6L时，A柱所形成的拖拽涡对后风挡及行李箱盖上的气流也产生了影响，而在波长为L时拖拽涡只是到车顶部，这说明在不同波长的侧风作用下A柱对气动性能也产生了重要影响。

(a)λ=L

(b)λ=6L图18 波长不同时车身周围的涡量图

3 结论

(1)受到空间及时间变化的瞬态正弦侧风时，气动阻力系数、侧力系数及横摆气动力矩系数都呈现周期性变化；气动阻力系数周期性变化的频率是正弦侧风变化的2倍，而气动侧力系数及横摆气动力矩系数变化的频率与正弦侧风变化的频率基本一致。

(2)受到瞬态正弦侧风时，正弦侧风的波长越大，气动侧力系数及横摆气动力矩系数迹线趋势与稳态模拟及实验的变化趋势相似；波长越小，差别越大。

(3)受到不同波长的正弦侧风作用时，侧风的波长对气动侧力及横摆气动力矩系数相位变化产生重要影响，侧风的波长与车长相近时相位变化很大。

(4)在侧风作用下A柱对汽车的气动性能产生重要影响，侧风波长越长，A柱所产生的影响越大。

[1] 谷正气. 汽车空气动力学[M].北京:人民交通出版社, 2005.

[2] Fuller J, Matt B, Nikhil G, et al. The Importance of Unsteady Aerodynamics to Road Vehicle Dynamics [J]. Journal of Wind Engineering and Industrial Aerodynamics,2013, 117(6):1-10.

[3] Dominy R G, Ryan A. An Improved Wind Tunnel Configuration for the Investigation of Aerodynamic Cross Wind Gust Response [J]. SAE Paper, 1999-01-0808.

[4] Raffaele V, Ferrand V, Arthur D, et al. Forces and Flow Structures Evolution on a Car Body in a Sudden Crosswind[J]. Journal of Wind Engineering and Industrial Aerodynamics,2014, 128(5):114-125.

[5] Wang Bin, Xu Youlin. Safety Analysis of a Road Vehicle Passing by a Bridge Tower under Crosswinds [J]. Journal of Wind Engineering and Industrial Aerodynamics,2015, 137(137):25-36.

[6] Hrvoje K, Kyle B, Ahsan K.Transient Cross-wind Aerodynamic Loads on a Generic Vehicle due to Bora Gusts [J]. Journal of Wind Engineering and Industrial Aerodynamics,2012, 111(12):73-84.

[7] Guilmineau E. Computational Study of Flow around a Simplified Car Body [J]. Journal of Wind Engineering and Industrial Aerodynamics, 2008, 96(6/7): 1207-1217.

[8] Cheng S Y, Tsubokura M, Okada Y, et al. Aerodynamic Stability of Road Vehicles in Dynamic Pitching Motion[J]. Journal of Wind Engineering and Industrial Aerodynamics, 2013, 122(11): 146-156.

[9] Emmanuel G，Francis C.Numerical and Experimental Analysis of Unsteady Separated Flow behind an Oscillating Car Model [J]. SAE Paper,2008-01-0738.

[10] 龚旭, 谷正气, 李振磊,等.侧风状态下轿车气动特性数值模拟方法的研究 [J].汽车工程，2010,32(1):13-16. Gong Xu,Gu Zhengqi,Li Zhenlei,et al.A Study on the Numerical Simulation of Car Aerodynamic Characteristics under Crosswind Conditions[J].Automotive Engineering,2010, 32(1):13-16.

[11] 王夫亮, 胡兴军, 杨博,等.侧风对轿车气动特性影响的稳态和动态数值模拟对比研究[J].汽车工程, 2010,32(6):477-481. Wang Fuliang, Hu Xingjun, Yang Bo, et al. A Study on the Comparison between Steady and Dynamic Numerical Simulations of the Crosswind Effects on Car Aerodynamic Characteristics [J]. Automotive Engineering, 2010, 32(6):477-481.

[12] Carsten P, Zhang X. Influence of Uncertainties on Crosswind Stability of Vehicles[J].Procedia IUTAM, 2015, 13: 98-107.

[13] Cheng S Y, Tsubokura M, Nakashima T, et al. Numerical Quantification of Aerodynamic Damping on Pitching of Vehicle-inspired Bluff Body[J].Journal of Fluids and Structures, 2012, 30(4): 188-204.

[14] 谷正气，陈阵，黄泰明,等.基于改进LRNk-ɛ模型的汽车气动特性研究[J].中国机械工程，2015,26(18):2550-2555. Gu Zhengqi，Chen Zhen, Huang Taiming, et al. Research on the Aerodynamic Characteristics of the Vehicle with an Improved LRNk-ɛ Turbulence Model[J].China Mechanical Engineering, 2015, 26(18): 2550-2555.

[15] 杨易, 徐永康, 聂云,等.非定常来流对汽车气动升力瞬态特性的影响[J].中国机械工程, 2014,25(12):1681-1686. Yang Yi, Xu Yongkang, Nie Yun, et al.Effects of Unsteady Stream on Transient Characteristic of Automotive Aerodynamic Lift[J].China Mechanical Engineering, 2014,25(12): 1681-1686.

[16] Tsubokura M, Andrew K, Keiji O, et al.Vehicle Aerodynamics Simulation for the Next Generation on the K Computer: Part 1 Development of the Framework for Fully Unstructured Grids Using up to 10 Billion Numerical Elements [J]. SAE Paper, 2014-01-0621.

[17] 汪怡平,王文龙,杨雪,等.超低马赫数空腔流诱发自激振荡数值模拟[J].中国公路学报,2015,28(7): 121-126. Wang Yiping, Wang Wenlong, Yang Xue, et al. Numerical Simulation for Self-oscillation Evoked by Cavity Flow at Ultra Low Mach Numbers [J]. China Journal of Highway and Transportation, 2015, 28(7):121-126.[18] Zhu Zhiwen.LES Prediction of Aerodynamics and Coherence Analysis of Fluctuating Pressure on Box Girders of Long-span Bridges [J]. Computers & Fluids, 2015, 110(30):169-180.

[19] Mo H M, Hong H P, Fan F. Estimating the Extreme Wind Speed for Regions in China Using Surface Wind Observations and Reanalysis Data Long-span Bridges Subjected to Crosswind[J]. Journal of Wind Engineering and Industrial Aerodynamics, 2015, 143(8):19-33.

[20] Ikeda J, Tsubokura M, Nakae Y,et al.A Numerical Analysis of Unsteady Aerodynamics of Road Vehicle during Lane-change Maneuvering[C]//ASME 2013 Fluids Engineering Division Summer Meeting. Lake Tahoe, 2013: V01CT19A004:1-10.

[21] Mehrdad R, Ahmadreza K.Numerical Analysis of Airflow around a Passenger Train Entering the Tunnel [J]. Tunnelling and Underground Space Technology,2015, 45(45):203-213.

[22] Krajnovic S L, Davidson L. Flow around a Simplified Car, Part 2: Understanding the Flow [J]. Journal of Fluids Engineering, 2005, 127(5): 919-928.

[23] Bruneaua C H, Creusé E, Gilliéronc P, et al. Effect of the Vortex Dynamics on the Drag Coefficient of a Square Back Ahmed Body: Application to the Flow Control[J]. European Journal of Mechanics—B/Fluids, 2014, 45(5): 1-11.

(编辑 陈 勇)

Analysis for Effects of Transient Crosswinds with Different Wave-lengths on Vehicle’s Aerodynamics Performance

Huang Taiming1,2Gu Zhengqi1,3Feng Chengjie1Chen Zhen1

1.State Key Laboratory of Advanced Design and Manufacture for Vehicle Body，Hunan University,Changsha，Hunan,410082 2.Hunan Institute of Science and Technology,Yueyang,Hunan,414006 3.Hunan University of Arts and Science,Changde,Hunan,415000

The large eddy simulation was used to investigate the vehicles subjected to transient sinusoidal crosswinds, and the transient crosswinds were changing in time and space, which was realized by the user defined function(UDF) to control the boundary conditions. The effects of the transient crosswinds with three different wave-lengths on the coefficient of the aerodynamic forces were analyzed, and the results were compared with the experimental and the quasi-steady simulation. The results show that: the coefficients of the aerodynamic forces are changing in periodic when the vehicles subjected to the transient sinusoidal crosswinds, but the change frequency of the coefficients of the drag forces is two times of the coefficients of lift and yawing moments. The changing range of the coefficients of drag forces are gradually decreased when the wavelengths of the crosswinds are reduced. The A-pillar has important influences on the vehicle aerodynamic performances in crosswinds.

large eddy simulation(LES); transient crosswind; wave-length; coefficient of aerodynamic force

2015-12-14

国家高技术研究发展计划(863计划)资助项目(2012AA041805)；中央财政支持地方高校专项资金资助项目(0420036017)；湖南大学汽车车身先进设计与制造国家重点实验室自主课题(734215002); 长沙市科技计划资助重点项目(K1501011-11)

U469

10.3969/j.issn.1004-132X.2016.20.022

黄泰明,男,1982年生。湖南大学机械与运载工程学院博士研究生，湖南理工学院机械工程学院讲师。主要研究方向为汽车车身与空气动力学、整车性能分析与优化。谷正气,男,1963年生。湖南大学机械与运载工程学院教授、博士研究生导师,湖南文理学院教授。丰成杰,男,1991年生。湖南大学机械与运载工程学院硕士研究生。陈 阵,男,1988年生。湖南大学机械与运载工程学院博士研究生。