基于数学模型的预测钢材消费强度的研究
瞿云华,张焕成,张玉柱,韩闯闯
(1.东北大学 辽宁 沈阳 110819;2.华北理工大学,河北 唐山 063000)
基于数学模型的预测钢材消费强度的研究
瞿云华1,2,张焕成2,张玉柱2,韩闯闯2
(1.东北大学 辽宁 沈阳 110819;2.华北理工大学,河北 唐山 063000)
钢材消费强度;曲线拟合;趋势移动平均法;灰色预测
以2005~2014年我国不变价国内生产总值、钢材需求量数据为样本,运用数学模型理论建立了曲线拟合模型、时间序列模型、灰色预测模型,分别进行预测并综合分析得出曲线拟合模型为最优模型,并用此模型对中国2015~2020年钢材消费强度进行预测。
一、引言
由于钢铁消费强度与国民经济紧密相关,从某种意义上能反映一个国家的经济水平,因此对未来我国钢铁消费强度的预测变得尤为重要。因此钢铁消费强度的预测成为目前的研究热点。1987年,潘德惠[1]等人基于国外钢铁需求预测的方法,建立了钢铁消费强度与时间序列组合的模型,预测了中国2000年钢材的需求量。2007年,黄永强[2]等人在分析了钢材消费强度的基础上,以1980~2005年钢材消费强度数据为样本,对我国2006~2008年的钢铁需求量进行了预测。2009年,黄波[3]基于我国2003~2006年钢材消费总量的面板数据分析,建立了钢材消费模型,对我国2010年钢材的消费量进行了预测。2011年,张群[4]等人以我国1985~2007年钢材表观消费量和钢材消费强度数据为样本,运用岭估计法,建立了钢材消费强度的超越对数模型,结果表明GDP对钢材消费有促进作用。
本文以2005~2014年我国不变价国内生产总值、钢材需求量数据为样本,建立了曲线拟合模型、时间序列模型、灰色预测模型,对中国2015-2020年钢材消费强度进行预测。
二、模型建立与求解
(一)数据准备
参考中国统计年鉴[5]以及相关文献,查到2005~2014年我国不变价国内生产总值、钢材需求量[6]如表1所示。

表1 2005~2014年我国不变价国内生产总值、钢材需求量
注:GDPCP: Gross Domestic Product at Constant Price
研究表明,钢材消费强度、钢材需求量和国内生产总值三者之间存在以下关系
IUt=Dt/GDP
(1)
式中,IUt——钢材消费强度;Dt——钢材需求量;GDP——国内生产总值。
由(1)式可得到我国2005~2014年钢材消费强度如表2所示。

表2 2005~2014年我国钢材消费强度
为了直观的了解我国钢材消费强度随时间的变化情况,根据表2数据画成折线图1。

图1 2005~2014年我国钢材消费强度随时间的变化图
(二)曲线拟合模型
(1) 最小二乘法理论
线性最小二乘法是解决曲线拟合最常用的方法[7],令
f(x)=a1r1(x)+a2r2(x)+…+amrm(x)
(2)
其中,rk(x)是线性无关的函数,ak是未知系数(k=1,2,…,m,n)。
拟合原理是使yi(i=1,2,…,n)与f(xi)的距离δi的平方和最小,称为最小二乘准则。


(3)
即

(4)

RTRA=RTY
(5)
当{r1(x),…,rm(x)}线性无关时,R列满秩,RTR可逆,于是方程组(5)有唯一解
A=(RTR)-1RTY
2曲线回归
利用曲线回归对钢材消费强度与时间的关系进行拟合,比较各种曲线的拟合度(表3),取拟合度最好的曲线作为钢材消费强度与时间的关系曲线(图2)。

表3 模型汇总和参数估计
由表3可知,在众多回归模型中,拟合度最好的是二次曲线模型,R Square为0.965,P值小于0.001,非常显著。因此选二次曲线模型,建立回归方程为
y=-2.00758×10-5x2+0.08044x-80.56502
(6)
拟合可得如下曲线

图2 最小二乘法钢材消费强度与时间的拟合关系图
计算可得表4

表4 最小二乘法预测值与实际值比较
平均误差为0.99 %,这表明精确度比较高。
(三)趋势移动平均法模型
一次移动的平均数[8]为

(7)
二次移动平均数,其原理是

(8)


(9)
其中,t为当前时间值;T为由t至预测期的时间值;at为截距;bt为斜率。
根据移动平均值确定平滑系数。由(9)式可知
所以
(10)
因此

(11)
由式(9),类似式(11)的推导,可得
(12)
所以
(13)
类似式(11)的推导,可得
(14)
于是,由式(11)和式(14)可得平滑系数的计算公式为
(15)
利用Matlab软件编程时间序列预测模型,可得表5。

表5 时间序列法预测值与实际值比较
拟合可得图3曲线:

图3 时间序列法钢材消费强度与时间的拟合关系图
时间序列模型所拟合的直线方程为
y2=0.0165-3.7778×10-4x2
(16)
其中,x2为n-2014,n为所预测的年份。
平均误差为2.15%,因此精确度较高,结果比较可信。
(四)灰色预测Verhulst模型的建立
(1) 设x(0)为钢材消费强度原始数据序列,即

=(0.0188,0.0185,0.0183,0.0182,0.182,0.0181,0.0176,0.0172,0.167,0.0166)
(17)


(18)
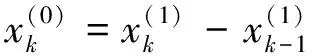
(19)


(20)

(21)
于是

(22)
(23)
(5) Verhulst模型为
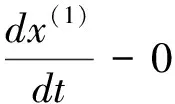
(24)
利用Matlab软件运行结果整理如表6。

表6 灰色预测法预测值与实际值比较
拟合曲线见图4:

图4 灰色预测法钢材消费强度与时间的拟合关系图
由表6可以得知平均误差为1.5%,较小,精确度相对而言较高。
灰色预测Verhulst模型的方程为:
y3=0.0209708-0.00217083×e0.0779106x3
(25)
(五)2015-2020年中国钢材消费强度的预测
由上面建立的三个模型比较可知,曲线拟合模型误差最小,所以用此模型预测中国2015~2020年钢材的消费强度,如表7所示。

表7 2015~2020年我国钢材消费强度的预测
三、小结
为了得到准确的预测值,运用三种不同的方法建立了三个模型,并进行比较,寻找最优模型对中国钢材消费强度进行预测。
模型一,利用10组数据建立曲线拟合模型,此方法的预测误差为0.99%,仅看此误差的数值可知此模型的准确度已经相当高,可以用来预测未来的钢材消费强度。模型二,即时间序列模型,此模型的预测误差为2.15%。模型三,即灰色预测Verhulst模型,运用此方法的预测误差为1.5%。
综合钢材消费强度趋势和模型误差可知:模型一,即曲线拟合模型为最优模型。
[1]潘德惠, 王海晏. 2000年我国钢材需求量预测. 信息与控制, 1987, 1: 49-53.
[2]黄永强, 尹继东, 李哲. 基于消费强度变化的钢材需求预测. 江西冶金, 2007, 27(3): 45-47.
[3]黄波. 基于面板数据的钢材消费模型估计与预测. 统计与决策, 2009, 1: 90-92.
[4]张群, 张超, 韩晓磊. 基于岭估计的中国钢材消费超越对数模型研究. 中国管理信息化, 2011, 14(24): 50-54.
[5]http://www.stats.gov.cn/tjsj/ndsj/2014/indexch.htm,2015.8.5.
[6]http://www.chyxx.com/data/201504/311544.html, 2015.8.5.
[7]万星火. 概率论与数理统计. 北京:科学出版社,2007.
[8]博克斯. 时间序列分析预测与控制. 北京:中国统计出版社,1997.1.
[9]党耀国. 灰色预测与决策模型研究. 北京:科学出版社,2009.12.
Evaluation Model of Core Competence of Chain Drugstore
FENG Bai-xia1, GE Feng-li1, CHEN Lei2
(1.College of Management, North China University of Science and Technology, Tangshan Hebei 063009, China;2.Graduate School of North China University of Science and Technology, Tangshan Hebei 063009, China)
chain drugstore; core competence; fuzzy comprehensive evaluation; evaluation model
There is no unified standard for evaluation of the core competence of drugstore chain. Based on the evaluation model of the core competitiveness of chain pharmacies, the evaluation model of the core competence is evaluated. First introduced the evaluation index of the core competitiveness of chain pharmacies; followed by the use of fuzzy comprehensive evaluation method to build the core competitiveness of chain drugstore evaluation model, select h pharmaceutical chain Co., Ltd, an empirical study on the evaluation of core competence, find out the weak links in the core competitiveness; finally puts forward strategies to improve the in view of the weak link.
2095-2708(2016)06-0034-07
F424.7
A

