数学复习如何加强审题训练
宁夏西吉一中 瓮彩霞
数学复习如何加强审题训练
宁夏西吉一中瓮彩霞
审题训练中要把握题意,准确理解概念,重视数形结合;运用数学思想及特例,注重基础知识;细读、多思、挖潜完成解题过程.
数学教学审题训练训练途径
“数学的真正部分是问题和解”.从典式到变式,从尝试到成功,充分利用数学课本中的习题与例题,研究探索怎样根据学生的特点,引导他们学会解数学问题,培养思维的灵活性、深刻性和创造性,实在是值得研究的课题。.为了提高解题能力,必须加强审题训练.应该怎样审题呢?可从以下几个方面入手.
一、准确把握题意,注意细微差别
审题是解题之始.认真、细致、全面、准确地审题,是解题成功的前提和关键.
例:设 a,b是两实数,A={(x,y)|x=n,y=n a+b,n∈Z},B={(x,y)|x=m,y=3m2+ 15,m∈Z},C={(x,y)|x2+y2≤144},是否存在a和b
使:(1)A∩B≠覫
(2)(a,b)∈C同时成立.这是一道用集合的语言表述的综合题.集合是现代数学最基本的概念之一.此题虽在灵活运用概念的能力上对学生的要求较高,但这些概念都是教材中最基本的知识.把na+b=3m2+15看成关于a,b变量的直线方程,涉及的是直线方程的概念和点到直线的距离公式等,是一道考察双基和能力的好题.
错误之一,将实数a,b与整数m,n混淆,从判断集合A、B的交集是否是集合C的子集,或者求集合A、B、C的交集入手造成错误.
错误之二,3n2-an-(b-15)=0理解为必存在两个整数n1,n2使其满足韦达定理,由此得出整数a,b均可被3整除的结论.再由a2+b2≤144,令 a=0,±3,…;b=0,±3,…去实验,把推理过程引向歧途.错误原因是概念不清,没有明确掌握题意和审题不细.
二、准确掌握概念,注意潜在条件
中学数学里,“没有概念就没有思路”.准确理解概念,它直接关系到公式定理的掌握及运算、推理和空间想象等能力的培养和提高,加强概念在审题中的作用是十分重要的.
例:设甲是乙的充分条件,乙是丙的充要条件,丙是丁的必要条件,则丁是甲的什么条件?
此题为充分必要条件的“复合”,是课本上的弱点.要用“推理 ”关系和“等价命题”来思考,即甲圯乙,乙圳丙,丙坩丁,复合起来看甲圯乙坩丁,丁是甲的什么条件不能确定,应为既不充分又不必要条件.充要条件是数学中的重要概念,揭示命题中条件和结论间的依存关系,应给予充分重视.
三、重视数形结合,注意运用特例
数和形是整个数学发展进程中的两大柱石.从“数”中去认识“形”,从“形”中去认识“数”就成为数学思维的基本方法之一.华罗庚曾告诫我们“数形结合百般好,割裂分家万事休”.数形结合的思维能力,不仅是中学数学能力与数学素质的主要标志之一,还是进一步学习高等数学和现代数学的能力基础,因此加强培养和训练这方面的能力,具有极其重要的意义.
例:函数y=sin(2x+5π/2)的图像的一条对称轴的方程是:
(A)x=-π/2(B)x=-π/4
(C)x=π/8(D)x=5π/4
如考虑到“数形结合”,画出y=sinα草图知其对称轴的方程是:α=π/2+kπ,即2x+5π/2=π/2+kπ,可把选项代之验证或解出x=kπ/2–π亦可得出答案(A).
数学思维分为逻辑思维、辨证思维和直觉思维.数形结合中的思维方法属于辨证思维,它和其他的数学思维方法一起,凝聚在丰富多彩的数学基础知识之中.审题中,数形结合思维能力的培养和训练,是提高解题能力和发展智力所必需的.
四、运用数学思想,注重基础知识
中学数学有两条红线,即数学基础知识和数学思想方法.无比丰富的数学内容,闪烁着许多共同的数学思维规律和方法,在平时的审题训练中应注重数学思想,着手双基,着眼能力,应从各个角度进行发散思维和分析探究,联想常用的解题方法,熟悉的例题与习题的解法,已知的定理、公式和法则等,尽量一题多解,充分发挥每道题的作用,从中选出最佳解题方案.经过长期有计划、有目的、有针对性地训练,学生在解题中会收到事半功倍的效果.
例:椭圆x2/a2+y2/b2=1(a>b>0),A,B是其上两点,线段AB的中垂线与x轴相交于点P(x0,0).证明:
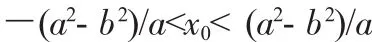
除常规解法外,可设参求解.设
A(a cosθ1,b sinθ1),B(a cosθ2,b sinθ2),
由|PA|2=|PB|2,
得:(a2–b2)(cos2θ1-cos2θ2)
=2ax0(cosθ1-cosθ2).
∵AB的垂直平分线与x轴相交,
故AB与y轴不平行,
即cosθ1≠cosθ2,
∴(a2-b2)(cosθ1+cosθ2)=2ax0,
即x0=(a2-b2)(cosθ1+cosθ2)/2a,
知-2〈cosθ1+cosθ2〈2,
∴-(a2-b2)/a 总之,审题训练是平时教学中的薄弱环节,应在总复习中加强辅导,审题的方法既多又灵活,但我的做法仅仅抓住了细读、多思、挖潜六个字,在这六个字上下功夫.在此基础上重视以上四种关系,使我们的学生能正确、迅速、准确地完成解题过程.

