巧设探究性问题 绽放异样光彩*——“等差数列的概念”教学设计体会

●周冬松 李 荣

(射阳县高级中学 江苏射阳 224300)



巧设探究性问题 绽放异样光彩*
——“等差数列的概念”教学设计体会

●周冬松 李 荣

(射阳县高级中学 江苏射阳 224300)

在数学教学中设置探究性问题是增加探究性教学空间的有效措施之一.力寻探究点，巧设探究性问题：紧扣数学概念的本质，多点并一问；注重课本例、习题的辐射作用，多例探结论；凸显数学课堂的完美性，要点回头问.探究性问题设计的思考：高水平、富有探究性的“问”是构建探究性问题教学的精髓；适时、富有指导性的“让”“引”是运用探究性问题教学、打造高效课堂的关键.

问题;探究性问题;探究点;高效课堂

新课程改革以来，新课程标准和新教材都积极倡导探究性教学，呼吁增加教师在数学教学中的探究性教学空间，将培养学生的探究能力和实践能力放在首要地位.笔者认为：在数学教学中设置探究性问题是增加探究性教学空间的有效措施之一.所谓探究性问题是指问题的条件或结论尚不明确，需通过探究去补充条件或完善结论的一类问题[1].相对于问题(即要求回答或解答的题目)，更有助于培养学生发现、提出解决问题的能力，有助于发展学生的创新能力.因此，在新课程理念中，数学探究性问题在教学中越来越受到重视，也备受广大师生的关注.

没有问题就没有数学教学，没有好的问题就没有好的课堂教学.那么，在平时的教学中，我们该如何设计问题呢？特别是如何增加问题的探究性呢？近日，笔者在江苏省射阳县第7届高中数学新课程优质课竞赛活动中上了“等差数列的概念”这节课，并作了一些尝试.以下是笔者在教学设计中的一些想法与做法，供大家参考.

1 力寻探究点，巧设探究性问题

1.1 紧扣数学概念的本质，多点并一问

在新授课中，离不开对数学概念的教学.要想使学生对数学概念有更为深刻的理解，教师不妨紧紧围绕数学概念的本质这一探究点，来巧设探究性问题.为了增强问题的探究性，可将多个反映同一本质的知识点合在一起来提出问题，即多点并一问.

比如，在本节课的开始，笔者引入了日常生活中出现的一些数列，然后充分挖掘等差数列的本质特征，并以此为探究点将等差数列定义的文字语言、符号语言、连等表示式合在一起，提出了“如何表示出这样的特点”这样一个问题.应该说，这个问题可给学生创设一定的思考空间与探究空间，因为至少有以下几种方法可以表示出这样的特点：

1)文字语言法.从第2项起，每一项与前一项的差为常数.

2)符号语言法.当n∈N*时，an+1-an=d(常数)；或当n∈N*且n≥2时，an-an-1=d(常数).

3)连等表示法.当n∈N*时，an+1-an=an+2-an+1.

如此一来，给学生创设了充分展示的空间，可将几个要点内容同时探究出来.

教学片段1

师：通过前面的研究，我们知道数列是按照一定顺序排成的一列数．下面，请同学们观察、思考下列情境：

情境1 2008年北京奥运会，女子举重较轻的4个级别体重组成数列：48,53,58,63.

情境2 1986年，人类在地球上观测到哈雷慧星第5次出现，最早在1682年，每隔76年观测到一次，年份依次为：1682，1758，1834，1910，1986.

情境3 NIKE(女)运动鞋尺码：25.5,25,24.5,24,……

从上述情境中抽象出的数列有什么共同特点呢？

生：从第2项起，每一项与它前一项所得的差都等于同一个常数．

师：很好！

追问：如何表示出这样的特点呢？

1.2 注重课本例、习题的辐射作用，多例探结论

课本中的例、习题是我们平时教学中最具有参考价值的素材，同时也最具有权威性.因此，课本例、习题的教学一直是授课的重中之重.如果教师在平时的教学中能注重课本例、习题的辐射作用，并以此作为探究点，来巧设一些探究性问题，教学效果一定会事半功倍.较为常见的做法之一是多例探结论，即不将结论直接告诉学生，而是先列举若干实例，然后让学生自己从中抽象概括出结论来.

比如，在处理本节课的练习时，笔者充分注意到了课本习题的辐射功能，列举了正反4个实例之后，提出“你从中发现了什么”这样一个问题，以引导学生进行观察、比较、分析与提炼.而设置这个问题的意图是引导学生学会猜想与归纳，并自然给出“an=pn+q(其中p,q为常数)一定是等差数列”的结论.

教学片段2

师：判断通项公式为如下所示的数列是否为等差数列？

1)an=0； 2)an=n2；

3)an=-2n+4； 4)an=3n+1.

生：通项公式为an=0，an=-2n+4，an=3n+1的数列都是等差数列，通项公式为an=n2的数列不是等差数列.

师：判断一个数列是否为等差数列，关键是看项an+1与项an之差是否为常数，即与n无关.

追问：你从中发现了什么？

1.3 凸显数学课堂的完美性，要点回头问

一节完美的数学课，不仅是课堂上教师、学生的精彩互动生成，同时最后恰到好处的课堂总结也是完美数学课堂的体现.如果能以此作为探究点，设置一些探究性问题,可能会使自己的课堂变得更精彩.“要点回头问”是巧妙设置探究性问题的常见方法之一，即在一类问题解决之后或课堂小结之时，设置一个问题引导学生回头看，当然这并不是简单的回顾，更多的需要学生进行思考与提炼.

比如，在本节课的最后，笔者提出了“判断等差数列的常用方法有哪些”这样一个问题，以引导学生构建处理这类问题的方法体系.同时，笔者又给出了一个追问，为下节课的学习抛出了一个悬念，进一步激发了学生的求知欲.

在杨万里的写意画里，这位有着浓厚文艺气质的放翁因花而醉，因醉而卧，因情而书的风神意态鲜活灵动，跃然而出。

教学片段3

师：通过本节课的学习，你知道判断等差数列的常用方法有哪些？

(学生讨论，自由回答.)

生1：验证当n∈N*时，an+1-an=d(常数)；或当n∈N*且n≥2时，an-an-1=d(常数)是否成立.

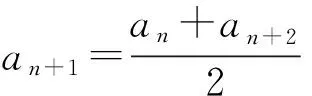
生3：看其通项公式是否为an=pn+q(其中p,q为常数)型，或其图像是否为直线型.

师：好！刚才同学们分别从3个角度来判断一个数列是否为等差数列，可以分别称为定义型方法、性质型方法、特征型方法.将来还可以看其前n项和是否为Sn=An2+Bn型，等等.

追问：通过刚才的讨论我们知道，an=pn+q(其中p,q为常数)型数列一定是等差数列，那么反之是否成立呢？

2 探究性问题设计的思考

在平时的教学中,我们设计问题时常常会暴露出一些不足：1)问题偏多，导致重点不突出.2)问题偏碎.因为问题偏多，自然导致问题偏碎.3)问题偏浅.问题多而碎，容易导致的结果是问题偏浅，即问题的思维价值与探究价值缺少.在这里笔者认为问题的来源不应当是教师将已有的知识转化为向学生简单的提问，而应当由教师创设一定的情境，使学生面临思维矛盾，从而主动地形成有价值的问题．因此，高水平的、富有探究性的“问”是构建探究性问题教学的精髓.

比如，在本节课的学习中，学生学习等差数列的主要难点是对等差数列概念的理解．因此笔者利用教材例题进行变式,再通过恰到好处的“问”,引起学生的思维冲突,让学生自己提出更有价值的探究性问题.这样的设计遵循学生的认知规律，问在“最近发展区”，有助于拓展学生的思维空间．

教学片段4

师：判断以下数列是否是等差数列?若是,请指出首项和公差.

1)-3，-2，-1，1，2，3；

2)1，1，1，1,1；

3)1,4,7,10,13,16,19，22[2].

生：1)不是等差数列；2),3)都是等差数列，公差分别为0,3.

师：很好！老师对第3)小题的数列设置了3个变式:

变式1 22，19，16，13，10，7，4,1.

变式2x，4x，7x，10x，13x，16x(其中x为常数).

变式3 ① 1,7,13,19;② 4,10,16,22.

上述数列都是等差数列吗？与第3)小题的数列有何联系？

生：上述数列都是等差数列，变式1相当于将原来的数列顺序倒过来，变式2相当于将原来的数列乘以同一个常数，变式3相当于取出原来的数列的奇数项或偶数项组成一个新的数列．

生(沉思了一会儿)：老师,已知a1,a2,a3,…,an,an+1,…,a2n是公差是d的等差数列，那么以下数列都是等差数列吗?

1)a2n,a2n-1,a2n-2,…,a3,a2,a1;

2)λa1,λa2,…,λa2n(其中λ为常数)；

3)①a1,a3,a5,…,a2n-1;②a2,a4,a6,…,a2n.

师:这位同学问得非常好!请大家一起探究.

2.2 适时、富有指导性的“让”“引”是运用探究性问题教学，打造高效课堂的关键

最近，江苏省盐城市教科院提出一种“让学引思”的教学主张．解读为“让学”就是要让学生亲身经历学习过程，在时间和空间上保证学生学习活动正常展开和学习行为真实发生.“引思”就是要引发、引导、引领学生思考，在形式和本质上保证学生大脑处于积极的思维状态.教师要在“让”与“引”上多研究，做到能“让”会“引”，确保“让”“引”并重；学生要在“学”与“思”上下功夫，做到善学真思，确保学思结合.笔者认为运用探究性问题教学正是实现这一教学主张的较佳途径．而运用探究性问题教学的效果，关键还在于教师适时、富有指导性的“让”和“引”．

比如，在本节课的例题教学中，笔者通过有度、到位地“让学”和及时、充分地“引思”，使学生对一系列探究性问题进行反思与回顾，提炼方法，探寻规律，让学生的思维能力得到进一步提升，从而探寻解决问题的一般方法．

教学片段5

师(让)：请同学们求出下列等差数列的未知项：

1) 3，a,5; 2) 3,b,c,-9[2].

师(引)：等差数列1),2)中每一项和它的前一项及它的后一项有什么联系？

师(引)：由这些等式,你能猜想出什么结论?

生:在等差数列{an}中，有

师(引、让):你能证明出这个结论吗?

生：在等差数列{an}中，因为

an+1-an=an-an-1(其中n≥2)，

所以

师(引、让)：在数列{an}中，如果对于任意的正整数n(其中n≥2)，都有

那么数列{an}一定是等差数列吗？

生：在数列{an}中，如果对于任意的正整数n(其中n≥2)都有

那么

an+1-an=an-an-1(其中n≥2)．

这表明，这个数列从第2项起，后一项减去前一项所得的差始终相等，因此数列{an}是等差数列．

实践让笔者感悟到，在教材每一章开始的新授课中，教师若能将本质概念、定理及思想内容巧设成一系列的探究性问题，以此引发、引导、引领学生“想学”“会学”“主动学”，那么该课堂定能绽放异样光彩！

[1] 钱云祥.探究性问题[J].中学数学教学参考，2008(1/2)：99-102.

[2] 教材编写组.苏教版普通高中课程标准实验教科书·数学5(必修)[M]．南京：江苏凤凰教育出版社,2015.

�2016-08-30；

2016-10-08

周冬松(1971-)，男，江苏射阳人，中学高级教师.研究方向：数学教育.

O122

A

1003-6407(2016)12-11-03