善于“捕捉”特征 寻找解题途径*

●杨玉坡

(英雄山中学 山东泰安 271000)



善于“捕捉”特征 寻找解题途径*

●杨玉坡

(英雄山中学 山东泰安 271000)

一个数学问题，往往表现出或隐含着诸如：数字、位置、图形、结构、差异等特征，解题时若善于“捕捉”这些特征，则有利于寻找到快速解决问题的途径.

捕捉;特征;寻找;解题;途径

一个数学问题，无论是条件、结论，还是数字、直观图像、整体结构等，往往表现出或隐含着某种特征.解题时，若善于分析、捕捉这些特征，并由此进行分析、变换、联想、构造，不仅有利于提高解题决策的敏捷性、寻找到快速解题的途径，而且可以有效地优化问题解决的过程.下面从几个方面来阐述，供参考.

1 “数字”特征

数学离不开“数字”，巧合的数字、共性的特征，看似偶然，往往暗含着对解题起导向作用的必然.只要善于观察、分析，从数字本身的变化、数字与数字之间的联系就能寻找解题的切入点[1].

例1 已知正数a,b满足ab=4，求证：

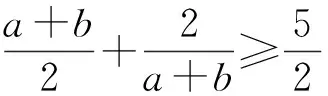
即

( )

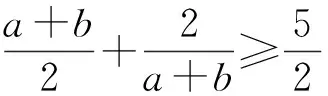
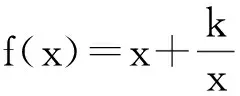
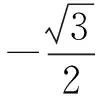
(2012年重庆市数学高考文科试题第5题)

分析 17°,47°暗含了特征47°-17°=30°，也暗含了本题可转化利用30°进行解题.

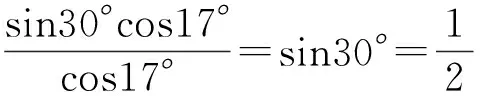
故选C.

点评 本题若分析不到位，则很难发现和利用数字(角)特征“47°-17°=30°”，从而解题思维受阻或无从下手.

2 “位置”特征

与图形(像)有关的一些数学问题都有它特定的位置关系，从与众不同的位置关系上寻找解题的切入点，可以明确解题方向，甚至可以收到不攻自破的解题效果.

例3 若直线y=kx+b是曲线y=lnx+2的切线，也是曲线y=ln(x+1)的切线，则b=______．

(2016年全国数学高考理科试题第6题)

分析 从2条曲线的公切线入手，建立方程组求解.

解 设曲线y=lnx+2上切点的横坐标为x1，则切线方程为

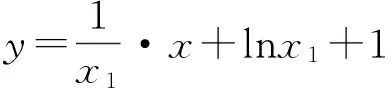
设曲线y=ln(x+1)上切点的横坐标为x2，则切线方程为

依题意可得

解得

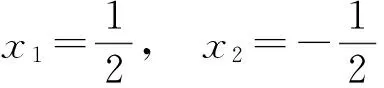
故

b=lnx1+1=1-ln2．

点评 解决本题的关键是抓住“直线y=kx+b是2条曲线的公切线”这一位置特征.

例4 已知变量x，y满足约束条件

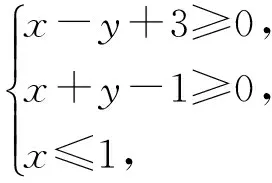
若直线y=k(x-1)将可行域分成面积相等的2个部分，则目标函数z=kx-y的最大值为______.

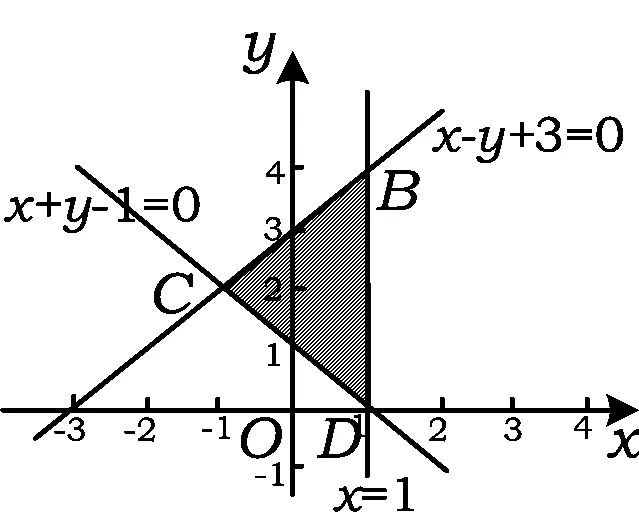
图1

z=kx-y=-3x-y.

平移直线-3x-y=0，易知当直线z=-3x-y经过直线x-y+3=0与直线x+y-1=0的交点C(-1,2)时，z=-3x-y取得最大值，且zmax=1.

点评 本题若不能够发现直线恒过定点这一位置关系，则很难处理好直线y=k(x-1)将可行域分成面积相等的2个部分，也就无法顺利解题.

3 “图形”特征

一些抽象的数量关系，若转化为具体的图形问题，从图形特征中寻找解题的切入点，则思路直观、清晰，有利于快速解题.

( )

分析 若用代数方法，设出直线l的方程，与双曲线方程联立后，利用判别式Δ≥0求解，则过程冗繁.若充分利用图形特征，则可使问题快速解决.

于是

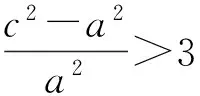
即

e2>4,

亦即e>2.故选D.

点评 若能对所求数学问题既分析其代数含义又挖掘其几何背景，也就是将抽象的数学语言与直观的图形结合起来，在代数与几何的结合中找出解题思路，则十分方便.求解圆锥曲线的离心率时，常利用平面图形的性质，利用图形特征使问题化难为易.

(2014年山东省数学高考理科试题第5题)

点评 本题将新定义的问题巧妙地迁移、转化为“直线与圆的位置关系”问题求解，可以看出这种构造应用具有创造性.

4 “结构”特征

数学问题条件或结论中常常隐含着某种特殊的关系，善于洞察并加以分析、加工和转化，可迅速找到问题解决的切入点.

例7 设x,y为实数，且满足

则x+y=______.

分析 条件中2个方程左边的结构形式相同，为此构造函数f(x)=x3+2 017x，并讨论其单调性和奇偶性即可达到解题的目的.

解 由已知，方程组可变形为

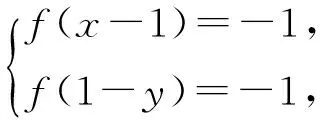
f(x-1)=f(1-y),

即

x-1=1-y，

亦即

x+y=2.

点评 若按常规方法求解此题，难度较大，甚至无法入手.这里通过构造函数，利用函数的奇偶性和单调性转化求解，方法巧妙，且过程简洁.

1)求证：点P的纵坐标为定值，并求出这个值；

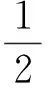
解 1)因为点P为P1P2的中点，所以

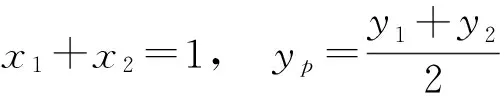
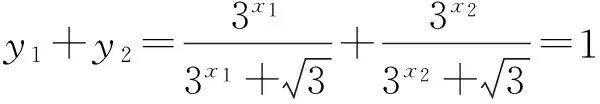
2)由x1+x2=1，得

y1+y2=f(x1)+f(x2)=1.

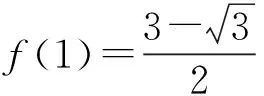
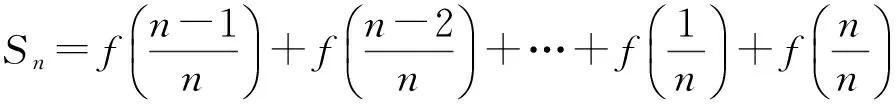
1+1+…+1+2f(1)=

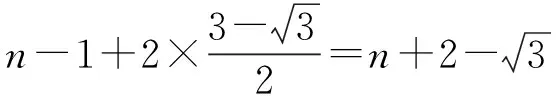
即

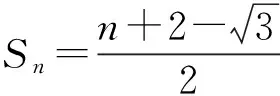
点评 本题在求和时，运用了第1)小题所得等式f(x)+f(1-x)=1得到通项的特征，即

由于距首末2项等距的2项相加和为定值，从而可以用倒序相加法求和.

5 “差异”特征

条件是解题的基础和依据，结论是解题的目标.善于捕捉条件和结论之间的“差异”关系，并以此启动和确定解题的切入点.

分析 条件中给出了2个“不等量”关系，结论探求的是“等量”关系.通过对这一差异 “点”的分析，获知解题的切入点就是化“不等”为“等”.

解 因为Sn≤n2+n-1，所以

S1=a1≤12+1-1=1，

即a1≤1.

(1)

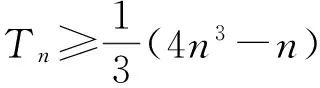
又a1>0，从而

(2)

故由式(1)和式(2)可得a1=1.

由Sn≤n2+n-1，即

(3)

因为

[12+22+…+(n-1)2]d2=

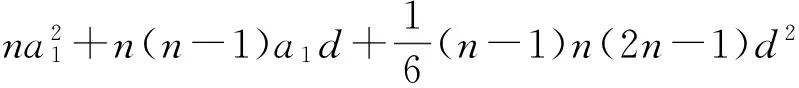
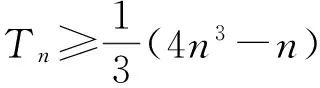
从而

(2n-1)d2+6d-8(n+1)≥0，

即

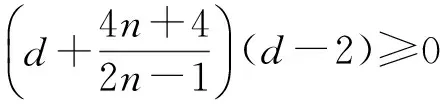
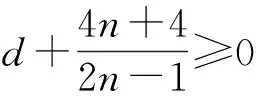
d-2≥0,

即d≥2，

(4)

故由式(3)和式(4)可得d=2.

点评 本题通过对“等”与“不等”的差异点进行分析和转化，使得不等式中的夹逼法则(如果实数x,a满足a≤x≤a(即x≥a且x≤a)，则必有x=a)在本题中起了重要的作用.

[1] 尹承利．例说寻找解题切入点的途径[J]．中学数学研究，2003(5)：25-27．

�2016-09-30；

2016-10-31

杨玉坡(1981-)，男，山东泰安人，中学一级教师.研究方向：数学教育.

O122

A

1003-6407(2016)12-18-04