数学命题策略探析*

●吴国建

(东阳二中 浙江东阳 322100)



数学命题策略探析*

●吴国建

(东阳二中 浙江东阳 322100)

作者介绍： 吴国建，男，1969年生，浙江东阳人，中学高级教师，现任浙江省东阳市第二高级中学校长.浙江省首届教育硕士、首届浙派名师班班长.曾获浙江省特级教师、金华市名师、东阳市拔尖人才等荣誉称号.辅导学生参加全国高中数学联赛等各级竞赛成绩突出，多次荣获全国高中数学联赛优秀教练员称号.曾主持浙江省首个高中数学特级教师工作室，现主持浙江省网络名师工作室.开发省市精品选修课程、网络推荐课程和基础教育微课程7门，发表文章近50篇，出版专著和参与编写教材教辅60多本，主持“基于教师学科理解力培育的自慧课堂研究”等省市级课题10余项.

数学题的命制是数学、教育学、心理学等多学科交叉的一个综合性工程．一道优美的数学题在符合知识点、难度等命制要求的同时往往蕴含了数学形式与内在美的和谐统一，既能深刻揭示数学的本质，展示数学思维的品质，也能充分展现命题者良好的数学素养．文章通过一些具体数学问题背景意义和命题过程的分析，阐述数学题命制的4种基本策略.

命题策略;一般与特殊;嫁接与组合;类比与推广;定量与定性

问题是数学的心脏，数学教学离不开解题．数学题的命制是数学、教育学、心理学等多学科交叉的一个综合性工程．一道优美的数学题在符合知识点、难度等命制要求的同时往往蕴含了数学形式与内在美的和谐统一，既能深刻揭示数学的本质，展示数学思维的品质，也能充分展现命题者良好的数学素养．一个优秀的数学教师不仅应当是一个解题高手，而且应当成为一个命题能手．本文结合笔者多次参与各级各类命题的实践，探析数学命题的4种基本策略．

策略1 一般与特殊

一般化是将已有特殊问题中的结论向更一般的情形推广，使原有的结论具有更一般的意义.特殊化是将数学中的一般结论通过数字化、赋值、图形定位等特殊手段展现在题目中.两者既可以独立运用，又可以交叉进行．一般问题特殊化与特殊问题一般化既是数学解题的重要思想，也是数学命题的常用策略．人教版《数学》选修2-1第70页有这样一道例题：

例1 过抛物线焦点F的直线交抛物线于点A，B，通过点A和抛物线顶点的直线交抛物线的准线于点D，求证：直线DB平行于抛物线的对称轴．

图1

这是一个非常巧妙的结论，题目可以变式如下：

变式1 如图1，过抛物线焦点F的直线交抛物线于点A,B，过点B作平行于抛物线对称轴的直线DB，交抛物线的准线于点D，则点A,O,D共线．

这2个问题结论成立的关键在于焦点与准线、抛物线准线与x轴交点和抛物线的焦点关于原点对称，这正是抛物线定义的本质.在日常教学中，直线有2种变换：一是旋转变换，如问题中直线AB随着直线倾斜角的变化而变化，这种变换不改变问题的结果；二是平移变换，直线平移变换变化的实际上是定点的位置，即题中点F的位置，平移变换后直线的位置需要怎样改变，是否还要保持原有的对称性？问题的结果是否会变化呢？基于这些问题的思考，产生了新的问题，其实质就是特殊情况一般化：

图2

变式2 如图2，在平面直角坐标系中，过点M(m,0)(其中m>0)作直线g与抛物线y2=2px(其中p>0)交于点A,B，设点N为点M关于原点的对称点，直线l过点N且与x轴垂直，直线AO与直线l相交于点D，求证：直线DB平行于x轴．

先看一道不等式证明题：

分析 因为

(1-x2)2x2= (1-x2)(1-x2)x2=

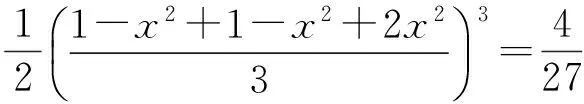
所以

即

这是一个一般化的结论，题中只涉及一个变量，结合基本不等式的性质可以通过增加变量、变换多项式的项数等方式，编拟出如下一系列问题：

1)已知0

2)已知0

3)已知0

进一步，结合基本不等式，对a+b,a+b+c,a2+b2等式进行赋值或放缩，可以得到表述更为简洁的不等式问题：

4)已知0

5)已知0

6)已知0

策略2 嫁接与组合

所谓嫁接，是将已有的一些结论作为一个整体移植到一个数学题内，使之成为整个题目的重要组成部分.而组合是将2个或者更多重要的知识或结论有机地组合在一起，形成一个完整的数学题．无论是嫁接还是组合，在命题过程中要讲究自然和谐，而不是生搬硬套，各部分之间应相得益彰，浑然天成．

例3 在解析几何中有以下结论：如图3，已知抛物线y2=2px上一点P，过点P作倾斜角互补的2条直线PS,PT，分别交抛物线于点S,T，则直线ST的斜率为定值．

图3 图4

为了改变考查形式，在命题时将之作为一部分，与其他知识或内容(如直线和圆)相融合，增加切线等内容，形成了以下变式：

变式3 如图4，已知抛物线C：y2=2px(其中p>0)，曲线M：x2+2x+y2=0(其中y>0).过点P(-3,0)与曲线M相切于点A的直线l，与抛物线C有且只有1个公共点B.

1)求抛物线C的方程及点A，B的坐标；

2)过点B作倾斜角互补的2条直线分别交抛物线C于点S，T(不同于坐标原点)，求证：直线ST∥直线AO.

例4 1)已知a>1,b>1，求证：

以上问题的解答过程启发了笔者的进一步思考：

它体现了均值在数轴上分布的稠密程度.那么是不是可以考虑

即

从而构造如下题目：

3)已知a>1,b>1，求证：

策略3 类比与推广

所谓类比，就是由2个对象的某些相同或相似的性质，推断出它们在其他性质上也有可能相同或相似的一种推理形式．类比是一种主观的不充分的似真推理，运用类比可以由某一问题的背景联想到相似的背景，由某一问题的结论联想到相似的结论，或由某一问题的解决过程联想到另一问题的解决过程．运用类比构造数学问题，应当特别注意问题的科学性．推广是指对一个数学问题的解决过程和结果进行进一步的分析研究得到新的结论，或得到启发从而构思出新问题的过程．类比需要的是2个存在某些相同或相似的研究对象，而推广需要的是原问题有进一步思考的空间和价值．

( )

A．若|F2M|<|F1N|，则∠MF2N为锐角

B．若|F2M|<|F1N|，则∠MF2N为钝角

C．若|F2M|<|F2N|，则∠MF2N为锐角

D．若|F2M|<|F2N|，则∠MF2N为钝角

本题的求解，可以直接运用双曲线的定义．而椭圆和双曲线作为2种重要的圆锥曲线，在几何性质上具有统一性，这种统一性正是联想的基础，由此及彼，往往可以编拟出许多数学问题．如将本题中的双曲线改为椭圆，其余不变，可得到如下变式：

图5 图6

( )

A．若|F2M|<|F1N|，则∠MF2N为锐角

B．若|F2M|<|F1N|，则∠MF2N为钝角

C．若|F2M|<|F2N|，则∠MF2N为锐角

D．若|F2M|<|F2N|，则∠MF2N为钝角

仿照原题的解法，利用椭圆的定义可以求得(过程略).

例6 设a,b,c>0，求证：(a5-a3+3)(b5-b3+3)(c5-c3+3)≥(a+b+c)2.

分析 本题的证明需先证一个结论：

a5-a3+3≥a2+2.

由a5-a3+3-(a2+2)=

(a-1)2(a+1)(a2+a+1)≥0，

可得

a5-a3+3≥a2+2.

在此基础上，由均值不等式得

(b2+2)(c2+2)=b2c2+2b2+2c2+4=

即

由柯西不等式得

故 (a2+2)(b2+2)(c2+2)≥

从而 (a5-a3+3) (b5-b3+3)(c5-c3+3)≥

3(a+b+c)2,

得证．

分析此证明过程，可以发现a5-a3+3≥a2+2的证明起到了一个降幂的作用，实现了从五次到二次的巧妙过渡．而在(a2+2)(b2+2)(c2+2)≥3(a2+b2+c2)的证明过程中，根据轮换对称性，左边a2+2,b2+2,c2+2中任何2项组合都能证明结论．值得思考的是，如果将左边推广到(a2+2)(b2+2)(c2+2)(d2+2)，结论会怎样呢？由此，可编拟如下变式：

变式5 设a,b,c,d>0，求证：(a5-a3+3)(b5-b3+3)(c5-c3+3)(d5-d3+3)>

策略4 定性与定量

将定性的结论，通过数字化的形式以定量的方式呈现，也是数学命题的一种常用策略.这一策略比较适用于几何问题，要求命题者有较高的几何素养，对几何图形有较强的观察能力，对几何性质有较深刻的理解．

例7 在平面几何2个圆的位置关系中，有如下性质：如果2个圆相交，则公共弦所在直线与2个圆公切线的交点是2个切点的中点．如图7，已知⊙M和⊙N相交于直线PQ，直线ST为2个圆的公切线，直线PQ交直线ST于点G，则由GS2=GP·GO=GT2知G为ST的中点．

联想抛物线的性质，以过抛物线焦点的弦为直径的圆与抛物线的准线相切，因此可以将整个图形置于坐标系中，将准线看成2个相交圆的公切线，进一步研究相交弦的性质，可编制如下变式：

图7 图8

变式6 如图8，过抛物线Γ的焦点F(0，1)作斜率分别为k1,k2的2条不同直线l1,l2，且l1交抛物线Γ于点A,B，l2交抛物线Γ于点C,D，以AB,CD为直径分别作⊙M和⊙N．

1)求抛物线Γ的方程.

2)判断⊙M和⊙N的公共弦所在直线是否经过定点？若是，求出定点的坐标；若不是，请说明理由．

例8 用“定性与定量”的策略描述空间几何体中的正多面体.

我们知道，空间几何体中，正多面体只有5种，分别是正四面体、正六面体、正八面体、正十二面体和正二十面体，其中每个面都是三角形的只有正四面体、正八面体和正二十面体．

以正四面体为例，在正四面体靠近一个面的中心取一点，从这点出发，将四面体的各条棱投影到平面内，得到如图9所示的图形，它由3个三角形组成，每个三角形对应四面体的一个面，第4个面投影后变成大三角形，此时图形的每个顶点聚焦着3条边，因四面体每个顶点聚集3条棱．

图9 图10 图11

同理，利用中心投影，可从一个正八面体得出一个由7个三角形组成的图形(如图10所示)；可从一个下正二十面体得到一个由19个三角形组成的图形(如图11所示)，在每个顶点分别聚焦着4条边或5条边．

根据以上的分析，可以将每个面都是三角形的正多面体通过投影转化到平面上，此时得到的图形每个顶点有相同数目的边，可根据上述结论命制如下变式：

变式7 把一个三角形分成n个三角形，使在所得三角形的每个顶点处(包括大三角形顶点处)聚集着相同数目的边，求n的可能取值．

�2016-09-10；

2016-10-12

吴国建(1969-)，男，浙江东阳人，浙江省特级教师.研究方向：数学教育.

O12

A

1003-6407(2016)12-01-05