恶劣海况下船体波浪载荷的统计推断

邱强，陈敏康，潘良，虞昊

1中国船舶科学研究中心，江苏无锡214082

2海军驻上海江南造船（集团）有限责任公司军事代表室，上海201913

3飞行器海上测量与控制联合实验室，江苏江阴214431

恶劣海况下船体波浪载荷的统计推断

邱强1，3，陈敏康2，潘良3，虞昊1

1中国船舶科学研究中心，江苏无锡214082

2海军驻上海江南造船（集团）有限责任公司军事代表室，上海201913

3飞行器海上测量与控制联合实验室，江苏江阴214431

介绍恶劣海况下船体波浪载荷（包括波浪和合成弯矩）统计推断的计算方法，并以某一高速排水型船舶作为算例进行计算。首先，按30 min短期海况估算该船的船舯波浪弯矩、砰击弯矩和合成弯矩统计特征值并与测量结果进行比较；其次按4 h海浪稳定假设，给出统计推断；最后，对巨浪海况完成算例船舶的波浪弯矩和合成弯矩的统计推断，并简要分析船体的总纵强度。

波浪弯矩；砰击弯矩；合成弯矩；统计特征值；恶劣海况

0 引 言

科学、准确地估算作用在船体上的波浪载荷，尤其是船体在恶劣海况下的波浪载荷，是船体结构安全性分析必须面对的问题。恶劣海况下船体结构波浪载荷估算主要有估算理论和实船测试2个方面的困难。首先，从实船测试角度看，要投入资金进行海洋观测、研制测量仪表、组织人员并做好设备保障，以期在恶劣海况（或设计工况）下进行实船波浪载荷与响应测试，然而受自然环境约束，往往达不到预设的海浪条件，经常遭遇的是4～5级海浪，不得不就当前遭遇的海况条件完成测试。而对于大型、超大型船舶，希望能够充分反映实船运动的恶劣海况更加难以寻觅。因此，实船测量数据显得十分珍贵和重要，特别是高海情状态下的实船测量数据就更加弥足珍贵，经常作

为检验理论估算和模型试验的依据和标杆。比较著名实船试验包括：3艘荷兰驱逐舰的耐波性试验［1］，经检验其测量数据符合雷利分布；英国海军进行的2艘驱逐舰的耐波性试验［2］与船舶水弹性理论［3］的计算比较；以及近年的美国CG47巡洋舰的海上试验［4］（由于测试海况没有充分反映船体的运动和载荷响应，在水池中进行了模型补充试验）和理论计算等。这些研究结果反映了当时这些组织与机构对排水型船舶在高海情状态下的科研预报能力与水平。其次，从估算理论的角度看，目前已知的困难主要是由海浪存在的自由表面非线性引起的，在自由表面线性化后，描述船体的运动方程仍然是一个依赖频率系数的微分方程系统。为了与实测结果进行比较，Denis等［5］提出将通信理论中发展起来的线性理论与方法用于船舶的非规则波中的响应与载荷计算，但是，1959年，英国学者Tick［6］指出，这种方法只适合于线性系统，对依赖频率系数的微分方程系统是不适用的；美国泰勒水池原主任Cummis［7］将这种线性方法比喻为“给造船界穿了一双不合脚的靴子”，每前进一步就需要回头看看，检查一下物理模型与理论估算模型对应的适用程度。迄今为止，2个不同波浪频率同时激励下的船体波浪载荷估算模型仍然未见报道。

针对估算线性模型中的物理模型与数学模型假设不一致的问题，文献［8］提出了一种理性的估算方法，用统计学第一定理直接估算船舶波浪载荷及其响应的低阶统计矩，引入载荷熵理论计算船舶波浪载荷的概率分布及各种特征值，使得物理模型与实际模型保持一致。

本文在文献［8-9］的基础上，取某一高速排水型船舶作为算例船，模拟测试工况，详细估算该船的船舯波浪弯矩、砰击弯矩和合成弯矩统计特征值，并与测量结果进行比较，以进一步验证理性计算方法的有效性，进而对巨浪海况完成算例船的波浪弯矩和合成弯矩的统计推断。

1 计算方法与数值结果

在文献［8］的基础上，将遭遇的短期海况分解为一个接一个不同波高、不同周期的表观波，根据船舶航行当前遭遇的波高、周期，将船舶“定格”在该“规则波”工况下，逐个计算遭遇波高与周期状态下的船体波浪载荷（波浪弯矩、砰击弯矩、合成弯矩）极大值，然后统计这些波浪载荷的极大值，便可以按载荷熵理论估算出载荷极大值分布，以便对船体波浪载荷进行统计推断。通俗而言，就是先“数”浪，其次“数”载荷，然后统计载荷，给出统计推断。这一计算过程与实际的海上测量和统计过程是一致的。

1.1 计算对象及干模态计算结果

计算对象取一艘高速排水型船，船长126.0 m，排水量3 320 t，按船体重量及刚度分布计算获得位移振型模态和弯矩模态。图1所示为船体梁的位移振型模态曲线，图2所示为高速排水型船船体梁干结构的弯矩模态图。

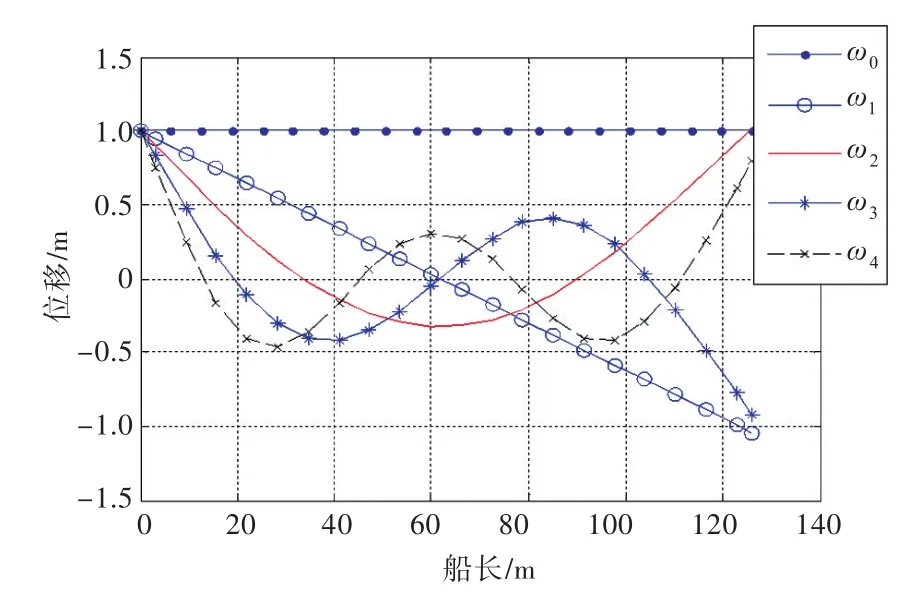
图1 船体梁的位移振型模态Fig.1 Vibration mode curve of vessel

图2 船体梁干结构的弯矩模态图Fig.2 Vertical bending moment mode

图1中：ω0为船体作为刚体的升沉振型；ω1为船体作为刚体的纵摇振型；ω2为船体梁的2节点弯曲位移振型；ω3，ω4分别为船体梁的3节点、4节点位移振型。图2中M2，M3，M4分别为船体梁的2节点、3节点和4节点弯曲的弯矩振型。

1.2 船体动置于规则波上的稳态响应

船体波浪载荷计算公式和步骤可参考文献［3］，首先计算高速排水型船在规则波激励下的纵向弯矩。航速分别取18，24与28 kn，波幅均取1 m，规则波波长取0.08～10.0倍船长范围的30个波长。

图3所示为高速排水型船航速18 kn时的主坐标 p2，p3，p4的波长船长比（λ/L）的幅值响应曲线，即船体梁的2节点、3节点、4节点频幅响应

曲线，由图可看出船的2节点弹性振动在波长船长比接近于1时响应较大。图4所示为航速在18 kn时船体梁的波浪弯矩幅值响应曲面。24与28 kn计算的图形与18 kn相似，此处省略。与文献［3］不同，图4所示的是船体梁波浪弯矩幅值响应曲面，而不是通常的二维曲线。

图3 弹性船体的波长船长比—幅值响应曲线Fig.3 Variation of|pi|with respect toλ/Lfor the hull girder

图4 弹性船体的波浪弯矩幅值响应曲面Fig.4 Amplitude response surface of wave induced bending moment

图3中，p2，p3，p4分别对应2节点、3节点和4节点振动响应的主座标幅值，为无量纲参数。

1.3 船体动置于规则波上的非稳态（砰击）响应计算

船舶在波浪中航行，船体不但有低频波浪弯矩作用，还可能发生砰击，船体同时要承受砰击弯矩的作用。在规则波响应计算中，通常认为低频波浪弯矩是稳态响应，砰击引起的响应是瞬态响应，其砰击过程可分为船艏底部砰击、艏外张砰击（动量矩砰击）及甲板上浪砰击。船艏底部（甲板上浪）砰击可以先用哈密顿方法求取脉冲响应函数，再用杜哈美积分求得船体梁的砰击响应弯矩。

砰击响应的研究可以追溯到上世纪30年代，Wagner［10］基于水上飞机的降落问题，进行了这方面的理论与试验研究工作，而后Ochi［11］，Tick［12］，Chung［13］等也开展了这方面的研究，对船艏底部的砰击提出了不同的看法，有的认为船艏底部与波面的相对速度超过则发生砰击，有的认为船艏底部与波面的相对速度超过则发生砰击，有的则干脆定义砰击应力超过6 MPa时发生砰击。文献［3］则认为船艏底部区域有足够的长度露出水面，再次入水时即发生砰击。本文注意到文献［11］提出的砰击压力公式中包含速度项，这意味着速度大，砰击压力大；速度小，则砰击压力小。而砰击次数并不直接影响弯矩大小，故部分采纳文献［3］的建议，将足够长度露出水面改为船艏底部有多少区域露出波面，则计算多大区域的砰击压力和砰击弯矩。具体计算时，根据航速和波长，逐歩提高波高；根据船艏底部露出波面的区域大小，按文献［11］建议的砰击压力公式计算砰击弯矩，而后计算动量矩砰击弯矩。

图5～图8所示为该船航速18 kn时的主坐标p0，p1，p2，p3的单位脉冲响应函数曲线。

图5 单位脉冲响应函数 p0（航向180°，航速18 kn）Fig.5 Unit impulse response curvep0（heading 180°，speed 18 kn）

图6 单位脉冲响应函数 p1（航向180°，航速18 kn）Fig.6 Unit impulse response curvep1（heading 180°，speed 18 kn）

图9～图12所示分别为在不同波长和波高状态下，用杜哈美积分求得船体梁的砰击弯矩和合成弯矩响应的典型曲线。

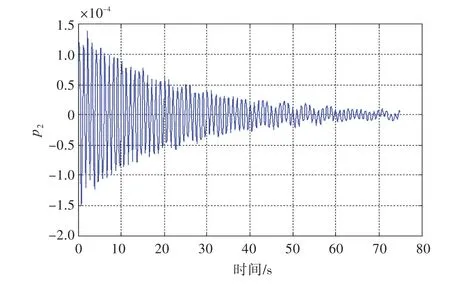
图7 单位脉冲响应函数 p2（航向180°，航速18 kn）Fig.7 Unit impulse response curvep2（heading 180°，speed 18 kn）

图8 单位脉冲响应函数 p3（航向180°，航速18 kn）Fig.8 Unit impulse response curvep3（heading 180°，speed 18 kn）

图9 船舯砰击弯矩响应曲线（顶浪，航速18.0 kn，波幅2.1 m，波长126 m）Fig.9 Bendingresponsecurveofonlyslamming（headwave，speed 18.0 kn，wave amplitude 2.1 m，wave length 126 m）

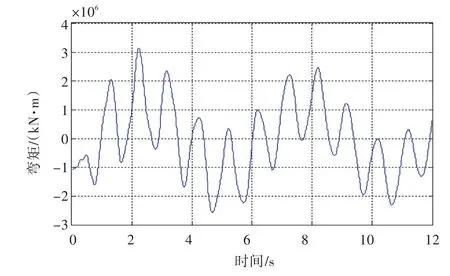
图10 船舯波浪弯矩叠加砰击弯矩后的响应曲线（顶浪，航速18.0 kn，波幅2.1 m，波长126 m）Fig.10 Resultant bending moment curve（head wave，speed 18.0 kn，wave amplitude 2.1 m，wave length 126 m）

图11 船舯砰击弯矩响应曲线（顶浪，航速18.0 kn，波幅2.1 m，波长126 m）Fig.11 Bending response curve of only slamming（head wave，speed 18.0 kn，wave amplitude 3.1 m，wave length 126 m）

图12 船舯波浪弯矩叠加砰击弯矩后的响应曲线（顶浪，航速18.0 kn，波幅2.1 m，波长126 m）Fig.12 Resultant bending moment curve（head wave，speed 18.0 kn，wave amplitude 3.1 m，wave length 126 m）

图13～图14所示分别为航速为18 kn时船舯砰击弯矩全幅值响应曲面，以及考虑相位的船舯中垂合成弯矩幅值响应曲面。

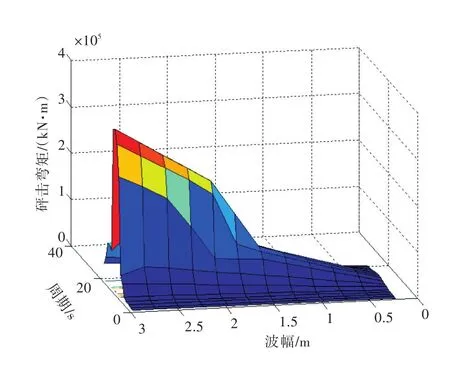
图13 船舯砰击弯矩全幅值响应曲面Fig.13 Full amplitude response surface of slamming bending moment

图14 船舯中垂合成弯矩幅值响应曲面Fig.14 Sagging response surface of resultant bending moment

2 随机波浪响应计算及实测数据比较

2.1 测试海浪条件简况

1975年12月29日，在我国南海对算例船开展高海情耐波性测试，测试海况如表1所示。根据实测海况条件，取ITTC谱形式，即有义波高H1/3=3.8 m，平均周期T1=8.4 s。实测波谱和模拟波谱如图15所示，按文献［8］计算获得到的第1小时的时域波浪曲线如图16所示，对应的波幅与周期联合概率分布如图17和图18所示。表1所示为模拟海情下的各统计特征与实测值比较。

表1 模拟海况的各统计特征与实测值Tab.1 Statistical value of pseudo and testing on the rough sea

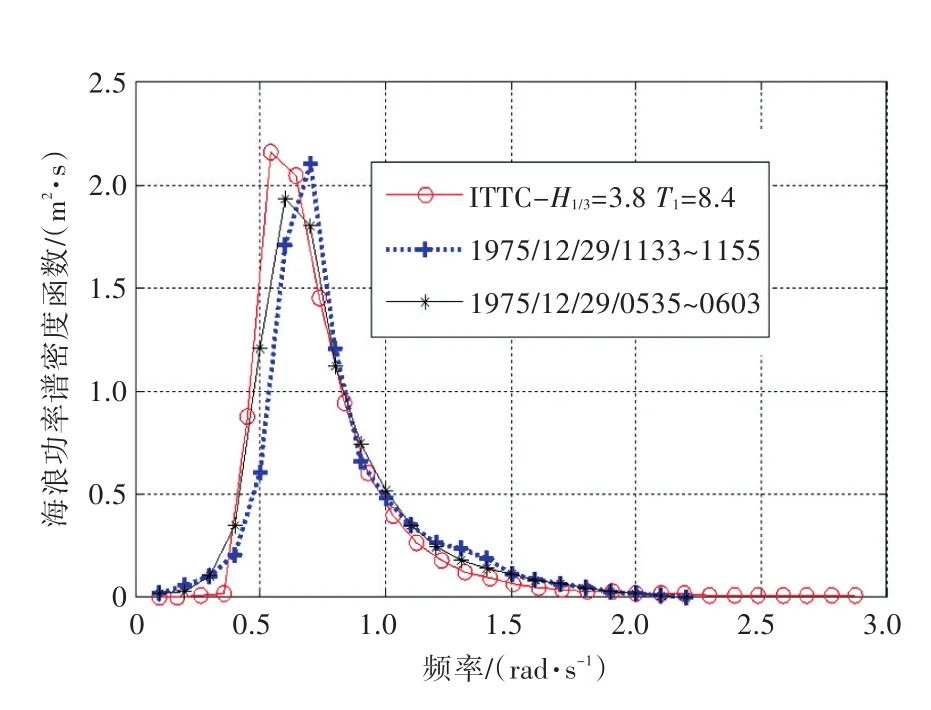
图15 实测波谱和模拟波谱Fig.15 Testing spectrum and simulation spectrum

图16 伪波浪现实Fig.16 Pseudo-wave elevation

图17 波幅与周期的统计直方图Fig.17 Histogram of wave amplitude and period

图18 波幅与周期联合概率密度分布Fig.18 Joint distribution of amplitude and period

2.2 计算与测量结果比较

为了估算算例船在测试状态下的合成弯矩1/3、1/10和1/100等统计特征值，首先按参考文献［14］的方法确定合成弯矩的概率密度函数，图19和图20分别给出了不同航速条件下的全幅和中垂合成弯矩的概率密度函数，根据概率密度函数

可以方便地计算出随机变量的各种统计特征值。表2所示为实船分别在航速18，24，28 kn时4 h航行状态的统计计算推断结果，表3所示为30 min的统计结果，便于与实测的统计结果进行比较。

图19 波浪和砰击作用下不同航速下船舯合成弯矩全幅值的概率密度与分布函数的比较Fig.19 Full resultant bending moment probability density at different speed impacted by wave and slamming

图20 波浪和砰击作用下不同航速下船舯中垂合成弯矩幅值的概率密度与分布函数的比较Fig.20 Sagging resultant bending moment probability density at different speed impacted by wave and slamming

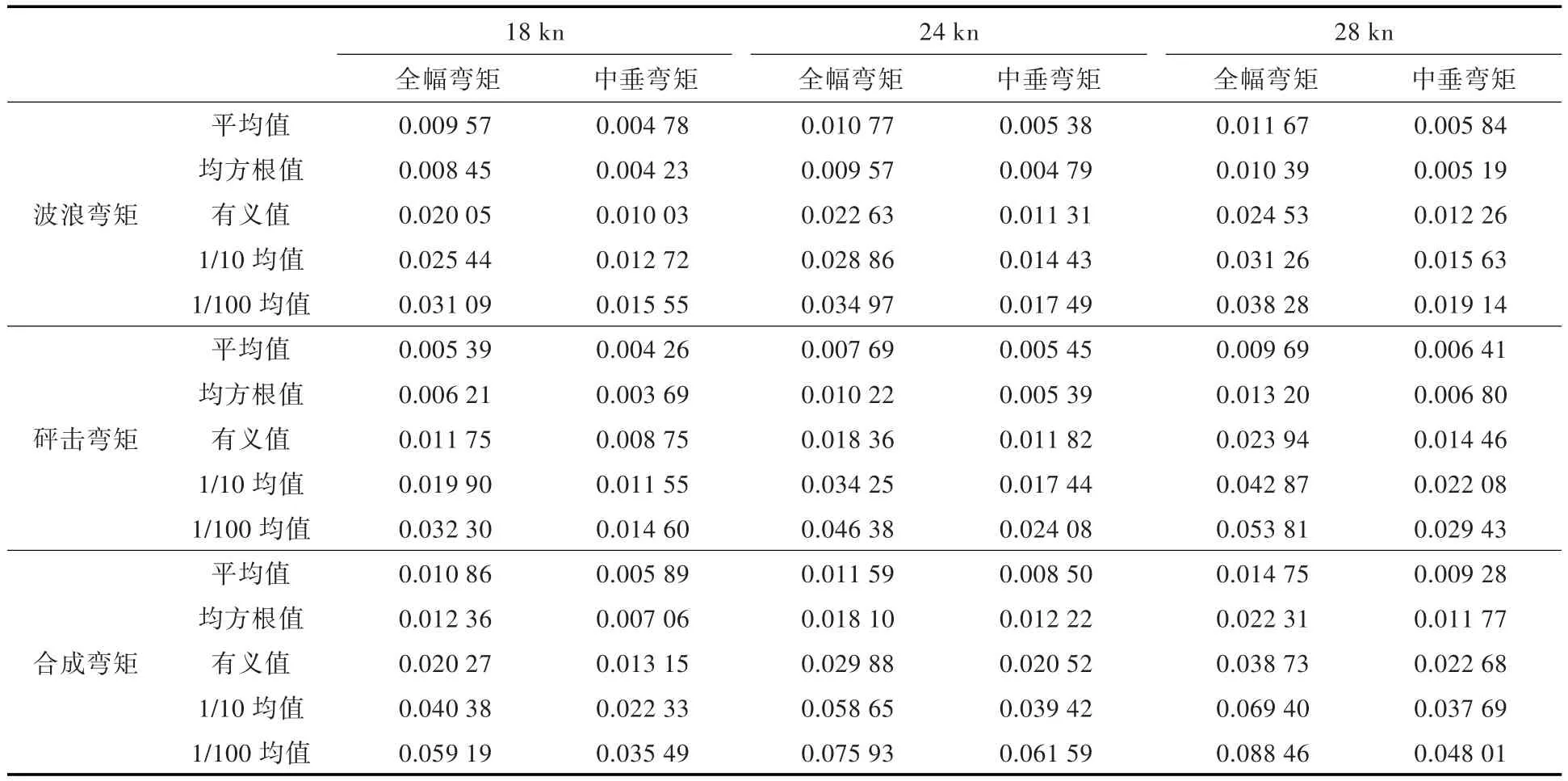
表2 波浪弯矩、砰击弯矩、合成弯矩的计算结果（无量纲）Tab.2 Calculated results of wave loads（nondimension）

比较表2和表3，可以看出：4 h的全幅弯矩计算结果与30 min的计算结果大致相当，基本符合人们的认识；不管是低频波浪弯矩统计值，还是砰击弯矩或合成弯矩的统计值，30 min的计算结果普遍小于4 h的计算结果。

根据试验测量状态，取30 min的估算结果与实测结果进行比较。表3列出了实船在顶浪18，24，28 kn时的测量结果与对应计算结果。

由表3可以看出：

1）低频波浪弯矩方面，不同航速18，24，28 kn的船舯波浪弯矩平均值、均方根值、有义值，测量值与概幅域计算和传统频域计算结果三者基本在同一水准上。

2）砰击弯矩方面，砰击弯矩为多频响应，传统的频域理论（谱方法）目前无法给出计算结果，原报告［15］中没有原始样本，仅给出了测量最大值，故实测砰击弯矩的统计分布难以确定，但测量的砰击弯矩最大值，在18 kn时，砰击弯矩小于本文计算的1/10均值；在24 kn时，砰击弯矩小于本文计算的1/10值；在28 kn时，砰击弯矩也小于本文计算的1/10平均值；这符合海上测量的一般规律。

3）合成弯矩方面，合成弯矩为低频波浪弯矩和砰击弯矩的叠加。传统频域理论（谱方法）目前无法给出计算结果，而合成弯矩大小是确定船体总纵强度的判断依据，因此十分重要。原实测报

告中给出了平均值、方差，没有给出有义值，但提出实测合成弯矩暂拟是指数分布，与本文的计算概率分布曲线大致相近。按本文的概率分布计算的合成弯矩特征值在航速18，24，28 kn时，最大合成弯矩均在有义值与1/10平均值之间，这也符合海上测量的一般规律。

表3 测量与计算结果比较（无量纲）Tab.3 Comparison between wave loads based on measured and calculated（nondimension）

3 巨浪条件下算例船的波浪弯矩统计推断

算例船的适航性试验海浪为6级，波高H3%为5.0 m。受自然条件的限制，期望的高海情适航性试验，波高H3%=6.0～8.5 m，即H1/3=4.542～6.437 m的基本试验条件没有遭遇。在技术条件下，可按前述的方法，通过仿真计算获得高海情适航性试验的波浪数据，并完成巨浪条件下的算例船波浪弯矩统计推断。

按照现行的我国国家海浪标准，有义波高H1/3=3.785 m为5级浪，称为大浪；6级浪的浪高标准为有义波高为4.0～6.0 m，称为巨浪。平均周期没有规定。而参考美国海军浪级标准，6级巨浪的有义波高为5.5 m，平均周期T1=7.9 s，谱型为ITTC谱，因该海浪环境规定比较明确，故采用这组数据。有义波高、平均周期、谱型确定后，按前述方法，可相继获得伪随机海浪现实、波高与周期的联合直方统计数据，而船体波浪弯矩、合成弯矩等已在规则波条件下计算完成，进行插值便可以完成统计计算。

根据总纵强度安全评估的需要，仅取相应的合成弯矩统计特征值。图21所示为伪随机海浪（H1/3=5.5 m，T1=7.9 s）的波高与波浪周期联合分布直方图。表4为4 h波浪条件下的船舯合成弯矩的矩统计值。船舯砰击中垂合成弯矩幅值响应曲面的形态可参见图4、图13和图14。

图21 波高与波浪周期联合分布直方图Fig.21 Histogram of wave amplitude and period

按表4所示的矩统计值可以按熵理论计算获得航速18，24及28 kn的船舯合成弯矩的概率分布。

表5～表7分别给出了在巨浪、顶浪情况下，在

18，24，28 kn航时算例船的船舯波浪弯矩、砰击中垂弯矩和考虑相位角的中垂合成弯矩4 h统计推断结果。

表4 船舯合成弯矩的矩统计值Tab.4 Midship resultant bending moment statistics

表5 船舯波浪弯矩、砰击弯矩、合成弯矩的统计特征值（4小时伪随机海浪，H1/3=5.5 m，T1=7.9 m；航速18 kn）Tab.5 Statistical characteristic values of midship wave，slamming and resultant bending moments（4 h pseudo-random wave，H1/3=5.5 m，T1=7.9 m；speed：18 kn）

表6 船舯波浪弯矩、砰击弯矩、合成弯矩统计特征值（4小时伪随机海浪，H1/3=5.5 m，T1=7.9 m；航速24 kn）Tab.6 Statistical characteristic values of midship wave，slamming and resultant bending moments（4 h pseudo-random wave，H1/3=5.5 m，T1=7.9 m；speed：24 kn）

表7 船舯波浪弯矩、砰击弯矩、合成弯矩统计特征值（4小时伪随机海浪，H1/3=5.5 m，T1=7.9 m；航速28 kn）Tab.7 Statistical characteristic values of midship wave，slamming and resultant bending moments（4 h pseudo-random wave，H1/3=5.5 m，T1=7.9 m；speed：28 kn）

传统的工程结构安全要求是保证在期望的使用期内，在最坏的使用条件下保证结构安全，要求最大载荷小于结构承载能力，并有一个安全系数，具体到船舶工程上，目前规范［16-17］采用的船舶结构总纵强度安全的评价方法中规定

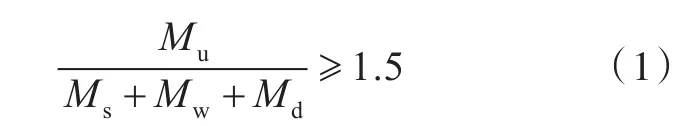
式中：Mu极限弯矩；Ms静水弯矩；Mw波浪弯矩；Md砰击弯矩。

实际情况中，砰击弯矩总是伴随波浪弯矩产生，砰击弯矩与波浪弯矩之间存在一定的相位角，故在某些情况下可简化为下式，比较符合实际情况，也便于计算。

式中：Mr=Mw+Md称为合成弯矩。为了进行强度比较，引入比较系数：

取不同的Mr，Mw，Md的统计特征值，便可以在不同的平均概率条件下进行强度比较。

就算例船而言，船体结构总纵强度的承载能力主要取决于甲板板架的压缩稳定性能力。现取算例船极限弯矩Mu=577 000 kN·m（作为常量考虑），静水弯矩Ms=25 000 kN·m（中拱，常数），Mr，Mw，Md分别取对应的1%平均值，分别按式（3）和式（4）进行计算，计算结果如表8和表9所示。

表8 中垂分析（4 h外推）的计算值结果（按式（3））Tab.8 Sagging analysis in extrapolation（4 hours）calculated value（per Equation（3））

表9 中垂分析（4 h外推）的计算结果（按式（4））Tab.9 Sagging analysis in extrapolation（4 hours）calculated value（per Equation（4））

由表8可以看出，砰击中垂弯矩随着航速的增加而快速增加，从而使得24，28 kn航速条件下，船体的合成中垂弯矩也快速增加，导致船体强度比较系数迅速下降。

至此补充了实船测试要求数据的不足，完成了巨浪条件下的算例船波浪弯矩统计推断。

4 结 语

本文介绍了海上船体波浪载荷的统计推断方法，其力学的基本思路就是将复杂的随机波浪弯矩（载荷）估算分解为随机波浪的“数浪”和确定性的非线性载荷动力计算二个问题分别给予处理，先“数浪”，获得波浪的波高与周期分布，然后再利用统计学第一定理“数载荷”，获得载荷的低阶统计矩；从概率论的角度利用载荷的统计矩逆求载荷的概率密度分布；获得概率密度函数后，便可以求得三一有义值和其他统计推断值，理论计算的统计过程与实际的测量数据的统计过程是一致的，测量统计结果与理论计算结果基本吻合，证实了本计算方法对于恶劣海况条件下，波浪弯矩、砰击弯矩和合成弯矩最小上限估算的有效性。

［1］ BLEDSOE M D，BUSSEMAKER O，CUMMINS W E. Seakeeping trials on three Dutch destroyers［J］.Transactions of Society of Naval Architects and Marine Engineers，1960，68（2）：39-137.

［2］ CLARKE J D.Measurement of hull stresses in two frigates during a severe weather trial［J］.Transactions of Royal Institution of Naval Architects，1982，124：63-83.

［3］ BISHOP R E D，PRICE W G.Hydroelasticity of Ships［M］.Cambridge：Cambridge University Press，1979.

［4］ HAY B，BOURNE J，ENGLE A，et al.Characteristics of hydrodynamic loads data for a naval combatant［C］// Proceedings of the 1st Conferences on Hydroelasticity in Marine Technology.Balkema，Rotterdam：［s.n.］，1994.

［5］ DENIS S M M，PIERSON W J.On the motion of ships in confused seas［J］.Transactions of Society of Naval Architects and Marine Engineers，1953，61（8）：71-77.

［6］ TICK J L.Differential equations with frequency-dependent coefficients［J］.Journal of Ship Research，1959，3（2）：45-47.

［7］ CUMMINS W E.The impulse response function and ship motions［J］.Schiffstechnik，1961，7（9）：101-109.

［8］ 邱强.非规则波激励下船舶运动及结构响应的理性估算方法［J］.船舶力学，1997，1（1）：40-43. QIU Qiang.Rationally-based prediction of ship motions and structural responses in irregular waves［J］. Journal of Ship Mechanics，1997，1（1）：40-43.

［9］ 邱强.一艘高速排水型船舶的波浪载荷估算和实测比较［C］//中国造船工程学会2013年船舶水动力学学术会议论文集.西安：中国造船工程学会，2013. QIU Qiang.Comparison of theory and experiment for wave loads of a ship［C］//Chinese Society of Naval Architecture and Marine Engineering Ship Hydrodynamic Academic Conference.Xi'an：Chinese Society of Naval Architecture and Marine Engineering，2013.

［10］ WAGNER H.Über stoss-und gleitvorgänge an der oberflä che von flüssigkeiten［J］.Zeitschrift Fur Angewandte Mathematik Und Mechanik，1932，12（4）：193-215.

［11］ OCHI M K.Slamming and impact［C］//Proceedings of the 6th International Ship Structure Congress.Boston，Cambridge，MA：MIT，1976.

［12］ TICK L J.Certain probabilities associated with bow submergence and ship slamming in irregular seas［J］. Journal of Ship Research，1958，22：30-37.

［13］ CHUANG S L.Experiments on flat-bottom slamming［J］.Journal of Ship Research，1966，10（1）：10-27.

［14］ 邱强.最大熵原理在船舶波浪载荷理性预报中的应用［J］.船舶力学，2004，8（4）：48-54.

［15］ 沈进威，周国华.南海某舰结构适航性试验［R］.无锡：中国船舶科学研究中心，1976.

［16］ 中国船舶工业总公司702研究所.水面舰艇结构设计计算方法：GJB/Z 119-99［S］.北京：总装备部军标出版社，1999.

［17］ 海军规范所.舰船通用规范：GJB 4000-2000［S］.北京：总装备部军标出版社，2000.

Statistics and analysis of ship wave loads under severe sea conditions

QIU Qiang1，3，CHEN Minkang2，PAN Liang3，YU Hao1

1 China Ship Scientific Research Center，Wuxi 214082，China

2 Naval Military Representative Office in Jiangnan Shipyard（Group）Co.，Ltd.，Shanghai 201913，China

3 Joint Lab of Ocean-Based Flight Vehicle Measurement and Control，Jiangyin，214431，China

A new calculation method of ship wave loads under severe sea conditions，including resultant moments and slamming moments，has been introduced，based on a high speed case.Results are firstly estimated under 30 minutes short term sea conditions，by comparing wave，slamming and resultant loads，then estimated under 4 hours stable sea states for higher statistics of extremes.Finally the overall strength of the ship has been briefly calculated.

wave induced bending moment；slamming bending moment；resultant bending moment；statistical characteristics；severe sea

U661.4

A

10.3969/j.issn.1673-3185.2016.06.008

2015-11-27

时间：2016-11-18 15:19

国家部委基金资助项目

邱强（通信作者），男，1956年生，高级工程师。研究方向：船体波浪载荷、结构变形与安全可靠性研究

http://www.cnki.net/kcms/detail/42.1755.tj.20161118.1519.016.html 期刊网址：www.ship-research.com

邱强，陈敏康，潘良，等.恶劣海况下船体波浪载荷的统计推断［J］.中国舰船研究，2016，11（6）：47-55. QIU Qiang，CHEN Minkang，PAN Liang，et al.Statistics and analysis of ship wave loads under severe sea conditions［J］.Chinese Journal of Ship Research，2016，11（6）：47-55.