水面舰船破损稳性的概率评估方法

马坤，邹梦瑶，吕振望

大连理工大学船舶工程学院工业装备结构分析国家重点实验室，辽宁大连116024

水面舰船破损稳性的概率评估方法

马坤，邹梦瑶，吕振望

大连理工大学船舶工程学院工业装备结构分析国家重点实验室，辽宁大连116024

水面舰船生命力的主要影响因素之一是舰船遭遇不同武器破坏下的薄弱性，而薄弱性主要由破损稳性决定。目前，舰船破损稳性评估主要运用确定性方法，但该方法不能全面评估舰船破损稳性。为了更加客观、全面地评估舰船破损稳性，探讨水面舰船破损稳性评估的概率方法，提出变区间线性插值计算残存概率Si的新方法并开发计算程序。以某水面舰船为例，计算各种破损情况的进水概率Pi以及残存概率Si，并累加所有破损情况Pi和Si的乘积，得到分舱指数A。研究表明：通过将分舱指数A作为评估指标并考虑不同武器和碰撞的综合破坏效应，概率方法可以实现水面舰船破损稳性定量且整体的评估，能为舰船初步设计阶段主船体的分舱优化以致提高舰船生命力提供一种解决途径。

水面舰船；破损稳性；概率方法；变区间线性插值

0 引 言

概率评估方法早期是由德国的Kurt Wendel教授于20世纪60年代提出，用于评估船舶的破损稳性［1］。随后，前苏联学者马涅采夫提出将船舶不沉概率作为统一的不沉性指标［2］。虽然概率方法提出得较早，但受制于计算机软、硬件的限制且概率评估方法的数值计算过程较为复杂，较少被运用在实船的破损稳性评估上。

然而，为了提高客船的安全等级，国际海事组织（IMO）开始采用概率方法评估客船的破损稳性。概率方法作为确定性方法的一种补充，被详细阐述在SOLAS 1974规范Res.A.265条款下，并最终作为货船的破损稳性评估方法之一被SOLAS 1992规范所采纳。之后，SOLAS 2009规范又将确定性的客船SOLAS 90标准与干货船基于概率方法的SOLAS 92标准协调为统一的概率破损稳性要求［3］。由此可见，概率方法在商船破损稳性评估上的运用已相对成熟。胡铁牛［4］基于概率方法分析了影响分舱指数A的主要因素和提高分舱指数A的方向及措施，并通过实船算例进行了验证。户艳宏［5］运用概率方法求取了客滚船分舱指数并进行了分析。

对于水面舰船，破损稳性评估主要是基于一系列确定性衡准，衡准中可残存的破损长度和稳性指标是根据第二次世界大战海战中的破损经验确定的。伴随着现代高科技作战武器的发展和舰船设计中对生命力的更高要求，引发了有关确定性方法在舰船设计上的局限性和适用性方面的思考［6］。为了更加客观、全面地评估水面舰船的破损稳性，荷兰学者Harsen等［7］根据IMO商船的概率方法提出了用于舰船的概率破损评估方法，提出了导弹和接触水雷这2种武器的破损点以及破损长度的概率密度分布，表明概率方法可以很好地用于舰船破损稳性评估。希腊学者Boulougouris和Papanikolaou［6，8-9］增加了SOLAS规范中有关碰撞破损的情况，通过计算所达到的分舱指数，比较了概率方法和确定性方法在评估舰船生命力方面的结果，提出了基于风险的舰船设计，并通过遗传算法对生命力予以了优化。由此可见，概率方法运用于水面舰船破损稳性评估和生命力优化是发展趋势。然而，我国学者针对水面舰船的相关研究还主要集中在舰船抗沉性或不沉性［10-12］、生命力的模糊评价［13］等方面。

综上所述，为了实现分舱指数A的数值计算，为我国水面舰船概率破损稳性衡准的制定提供一些参考，本文将研究适用于舰船破损进水概率Pi和残存概率Si的计算方法，提出Si的变区间线性插值方法，开发相应的计算程序，并给出某大型水面舰船的计算实例。

1 概率破损稳性计算模型

概率方法采用舰船破损后的残存概率作为衡量安全性的指标，总的残存概率即为所达到的分舱指数A。分舱指数A由全概率公式确定，为每个舱或舱组破损进水的概率Pi与进水后舰船不倾覆或沉没的概率Si的乘积的总和，即IMO在MSC.216（82）中制定了商船的概率破损稳性衡准，要求所达到的分舱指数A必须大于所要求的分舱指数R。对于商船，分舱指数R的大小主要与乘客数量、救生设备数量以及分舱长度等因素有关；对于舰船，分舱指数R的大小应该和舰船所指定的执行任务有关［7］，该指数目前还没有相关的计算准则。

商船的分舱指数A为3种装载工况下计算所得分项分舱指数的加权和，3种装载工况所对应的吃水分别为最深分舱吃水ds、部分分舱吃水dp和轻载航行吃水dl，因此，综合分舱指数可按下式计算：

式中，0.4，0.4和0.2分别为3种分项分舱指数的加权因子。对于商船，SOLAS 2009规范中只考虑了碰撞这一种破损效应，但是对于水面舰船，还需考虑导弹、鱼雷、触发水雷等武器的破损效应，因此，分舱指数A应为考虑了各个破损因素的分项分舱指数的加权和，其某一载况下的计算公式如下：

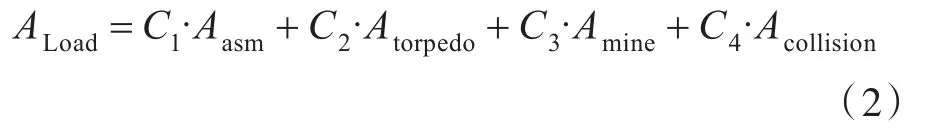
式中，C1，C2，C3和C4分别为导弹、鱼雷、触发水雷和碰撞的加权因子。加权因子的确定还需后续进行深入研究，本文暂时都取为0.25。

2 破损进水概率Pi的计算

2.1 破损点和破损长度的概率密度分布

SOLAS 2009规范中假定商船的破损进水是由碰撞造成的，碰撞情况下的破损点以及破损长度的概率密度分布符合分段线性分布。而对于水面舰船，不仅要考虑碰撞破损，还要考虑不同武器的破损效应，如导弹、鱼雷、触发水雷等。不同武器对应的破损点概率密度分布是不同的。在舰船

设计初期，由于缺乏大量真实的破损数据，一般假定武器效应的破损点的概率密度沿船艉至船艏方向符合分段线性分布或者正态分布［8］，本文假定为分段线性分布，如图1所示。导弹的最大概率密度在船舯，触发水雷在船艉至船舯范围的概率密度为0，鱼雷沿船长方向的概率密度相等［15］。

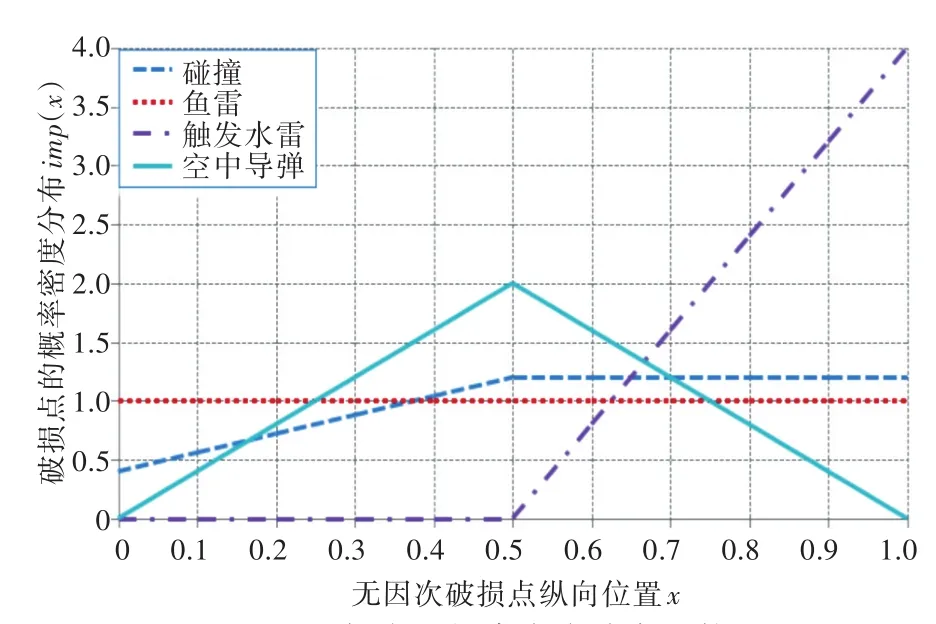
图1 破损点的概率密度分布比较Fig.1 Comparison of probability density distribution with impact point

破损长度的概率密度分布是基于防御分析中的损伤函数，其中对数分布最符合武器破损的真实情况［9］。本文在此基础上将其简化为分段线性分布［16］，如图2所示。

图2 破损长度的概率密度分布Fig.2 Probability density distribution of damage length

2.2 破损进水概率计算方法

在已知破损点和破损长度的概率密度分布的前提下，可以求得破损区域的进水概率Pi。假设破损区域的横舱壁位置为x1和x2，破损点的位置为x，破损范围以破损点为中心对称分布且破损长度为 y，如图3所示。在该区域，破损长度y的最大值 ymax=x2-x1。假定破损范围的最左端与x1重合，则x=x1+y/2；假定破损范围的最右端与x2重合，则x=x2-y/2。

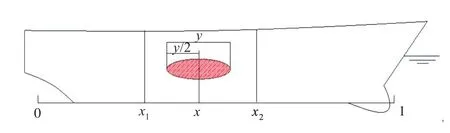
图3 破损区域示意图Fig.3 The sketch of damaged zone

对于该破损区域，破损进水概率Pi的计算可以通过破损点的概率密度函数imp(x)以及破损长度的概率密度函数Dam(y)的二重积分来实现，积分公式如下：

由式（3）可以看出，内层和外层函数的积分范围是相互制约的。本文将二重积分转化为单重积分，假设imp(x)=ax+b，Dam(y)=ky+c，单重积分函数的计算主要在于确定系数a，b，k和c。

2.3 多舱同时破损进水的概率

根据SOLAS 2009规范，Pi表示单舱i作为单区域破损后的进水概率，Pi+j表示i舱和j舱作为相邻两个区域破损进水的概率，Pij表示相邻的i舱和j舱同时破损进水的概率，三者满足式（4）：

同理，三舱连破进水的概率满足式（5）：

由此可见，相邻多舱同时破损进水的概率可以通过单区域和多区域破损进水的概率组合得到。

3 破损残存概率Si的计算

舰船破损后的残存概率Si一般可以通过准静态概率研究方法和动态进水/倾覆概率研究方法来计算［8］。准静态概率研究方法是根据舰船的确定性衡准演变而来，利用由破损后的复原力臂GZ曲线和风倾力臂曲线所围成的面积之比来计算破损后的残存概率。动态进水/倾覆概率方法是用时域仿真模拟舰船进水和倾覆，评估可能的破损情况并计算残存概率。本文中残存概率Si的计算采用准静态概率研究方法。

3.1 准静态概率研究方法

目前，世界主要海军强国均制定了各自的舰船破损稳性规范，对破损舰船的浮态和稳性均提出了相应的要求。浮态方面主要是通过最小干舷、限界线高度、纵倾程度及静平衡角来规定，稳性方面主要体现在破损后的初稳性高、GZ曲线特

性以及A1/A2等方面。国外舰船破损稳性规范各参数的定义如图4所示。

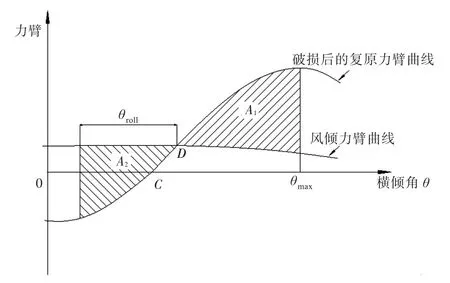
图4 舰船破损稳性规范各参数定义Fig.4 The definition of parameters in warship damaged stability criteria

舰船破损后，对于不对称进水的情况，会产生一个横倾角θC。风倾力臂曲线与复原力臂曲线相交于D点，对应的角设为θD。倾覆角θmax（即稳性消失角）取45°和进水角之间的较小者，在θD和θmax之间，风倾力臂曲线和复原力臂曲线围成面积A1。在风浪的联合作用下，舰船向来风一侧横摇至角θroll，在该角度范围内，风倾力臂曲线和复原力臂曲线围成面积A2。

本文主要借鉴英国和美国海军的破损稳性衡准，如表1所示。

表1 舰船破损稳性衡准Tab.1 Current UK and US damage stability criteria for surface combatants

由表1可以看出，英国和美国海军的破损稳性衡准具有相似性，但也存在着很多差异。两国海军的衡准均按照分舱长度Ls来对假定破损长度进行规定，在考虑突风和计算精度的情况下，均要求面积A1＞1.4A2［17］。根据以上舰船破损稳性衡准，希腊学者Boulougouris和Papanikolaou提出了用于概率破损稳性评估中的计算残存概率Si的方法。由于英、美两国海军规范在计算破损稳性时的风速要求大致相同，所以根据两国舰船破损稳性衡准计算残存概率Si的方法也基本相同，如表2所示。

表2 残存概率的计算方法Tab.2 The calculation method for the probability of survival

对于不满足Si=0或Si=1的破损情况，需要进行插值以计算残存概率Si。由表2可以看出，首先需计算出破损舰船的浮态和稳性，然后根据假定风速计算风倾力臂，利用破损后的GZ曲线和风倾力臂曲线在不同横摇角下所围成三角形的面积比例来计算破损后的残存概率Si。当θroll=15°时，如果纵倾水线淹没进水点或A1≤1.05A2，则Si=0；当 θroll=25°时，如果最小干舷≥0.6 m且A1＞1.4A2，则Si=1。

因为在判断Si=0和Si=1时θroll分别为15°和25°不满足线性插值中单一变量的要求，所以对于某种不满足Si=0或Si=1的破损情况，虽然计算出了A1/A2的值，但是不能直接在区间［1.05，1.4］内进行线性插值。此外，每一种破损情况所对应的实际的θroll也不相同，所以需要根据实际的θroll和A1/A2这2个参数来对残存概率Si进行计算。为了解决这一难题，本文提出了变区间线性插值方法，即先根据破损情况计算出实际的θroll以确定线性插值区间，然后再利用A1/A2的值在该区间内进行插值。下面将重点探讨变区间线性插值方法。

3.2 变区间线性插值

本文简化了水面舰船的舱室布置，仅对主船体进行纵向分舱，因此在破损进水后不会产生横倾，即静平衡角为0°。破损后的复原力臂曲线和风倾力臂曲线如图5所示。

图5 力臂曲线局部线性处理示意图Fig.5 Local liner processing of arm curves

由图5可以看出，GZ曲线的AC曲线段比较接近于直线，假设用直线AC进行替代。当横倾角接近于0°时，cos2θ≈1，风倾力臂曲线的AB曲线段假设用直线AB来替代。因此，由封闭曲线ABC围成的面积约等于直角三角形ABC的面积。当A点固定时，不同横摇角θroll对应的直线AB段的长度不同，则三角形ABC的面积比值等于直线AB段的长度比值的平方。假设θroll=25°，三角形ABC的面积为A25，即A2=A25；θroll=15°，三角形ABC的面积为A15，即A2=A15；θroll=x°，三角形的面积为Ax，即A2=Ax。根据面积比之间的相互迭代，不同横摇角下面积的比例关系如表3所示。

表3 不同横摇角下面积的比例关系Tab.3 Area ration under differentθroll

由表3可知，不同的横摇角对应于不同的线性插值区间，对于某种不满足Si=0或Si=1的破损情况，当求得破损情况下的横摇角θroll=x°时，线性插值区间确定为［1.05·（15/x）2，1.4·(25/x)2］，然后利用A1/Ax的值在该区间内进行线性插值计算残存概率Si。

4 实船算例

本文以某水面舰船为例，首先在NAPA软件中进行三维建模并进行破损稳性计算，然后按照上述Pi和Si的计算方法，在给定破损后的浮态和稳性曲线的前提下开发数值计算程序，实现分舱指数A的计算。

4.1 主要参数及分舱

本文以某舰船为研究对象，其基本参数如表4所示。

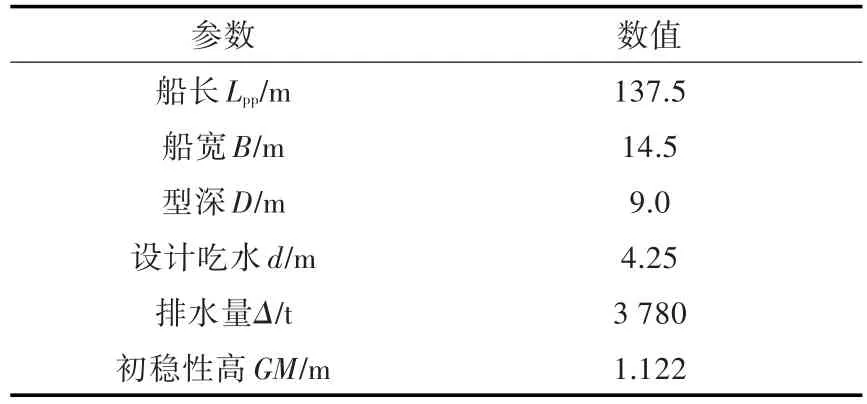
表4 某舰船的基本参数Tab.4 Basic parameters of a frigate

本文简化了舱室布置，仅对主船体进行纵向分舱。横向水密舱壁的位置如图6所示。本船共有14个横向水密舱壁，分成15个大隔舱，分别用No.1～No.15表示。

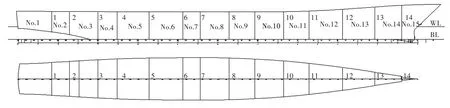
图6 主船体纵向分舱示意图Fig.6 Longitudinal subdivision of the frigate

4.2 破损组合

根据英国海军的确定性破损稳性衡准，假定破损长度取max（15%Lpp或21 m），经计算，本文中的最大破损长度为21 m。这一最大破损长度可导致5舱连续破损，共55种破损情况组合，如图7所示。但5舱连续破损只有一种情况且破损进水概率Pi≈0，对分舱指数A的贡献可以忽略，故最大

只考虑四舱连续破损。

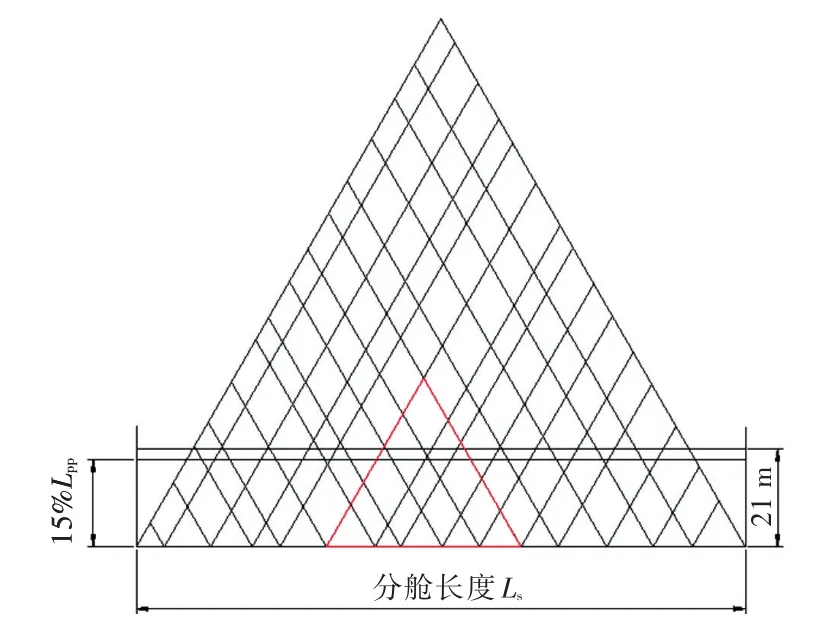
图7 破损舱室组合Fig.7 Damaged compartment combination

4.3 计算结果

Pi的计算根据式（5），单舱破损进水的概率Pi如表5所示。

表5 单舱破损进水概率Tab.5 The probability of damage for single room

在轻载装载工况下，以导弹造成的破损进水为例，单舱和两舱、三舱、四舱连续破损的进水概率Pi以及相应舱室破损的残存概率Si如图8所示。单舱破损对分舱指数A的贡献为0.153，两舱、三舱和四舱连续破损对分舱指数A的贡献分别为0.533，0.173和0.003，如图9所示。

图8 轻载工况、导弹命中条件下的Pi和SiFig.8 PiandSiin lightweight loading condition and hitted by a missile

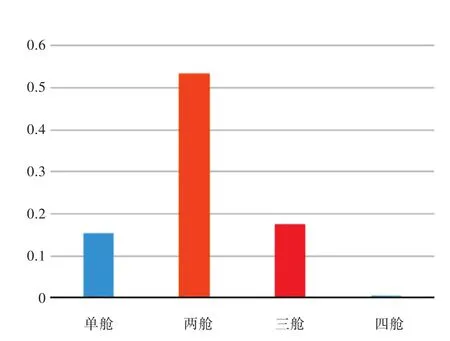
图9 分舱指数A的分布Fig.9 The distribution of the subdivision index A

由图8可知，对于给定的最大破损长度和纵向分舱，发生两舱连续破损进水的概率较大，较为危险的四舱连续破损进水的概率最小。若单舱破损进水之后的残存概率都为1，则舰船肯定不会倾覆。三舱和四舱连续破损进水之后的残存概率较小，若某些四舱连续破损进水情况下的残存概率等于0，则舰船肯定倾覆。由图9可知，对分舱指数贡献最大的是两舱连续破损，其次是三舱和单舱，四舱对分舱指数的贡献几乎可以忽略。

为了较为准确地评估舰船所达到的分舱指数A，在考虑3种不同装载工况的情况下，分别计算了碰撞及3种由不同武器造成的破损情况下的分舱指数，通过加权平均，得到该舰船综合分舱指数A=0.91。

5 结 论

对水面舰船破损稳性概率评估方法的研究重点在于如何计算所有破损组合的进水概率Pi和残存概率Si，本文围绕该要点展开研究，得到以下主要结论：

1）根据破损进水概率的基本积分公式，推导出了适用于不同武器的单区域破损进水概率积分公式，并采用VB编程开发出了舰船破损进水概率Pi的计算程序。

2）基于舰船确定性衡准条件，确定了残存概率Si=0和Si=1这2种特殊情况，针对Si≠0或Si≠1的破损情况，提出了变区间线性插值方法，并在给定破损后浮态和稳性曲线的情况下开发了残存概率Si的计算程序。

3）通过实船算例可以看出，本文所探讨的概率方法考虑了3种不同武器和碰撞的破损效应，计算了3种载况下的综合分舱指数A，与确定性方法运用衡准对每一种破损情况进行“通过或不通过”的定性评估相比，该方法能更加全面且定量地对舰船破损稳性进行评估，可为舰船初步设计阶段主船体的分舱优化提供一种单目标破损稳性评估方法。

［1］ PAPANIKOLAOU A，ELIOPOULOU E.On the development of the new harmonised damage stability regulations for dry cargo and passenger ships［J］.Reliability Engineering &System Safety，2008，93（9）：1305-1316.

［2］ 马涅采夫.船舶不沉性理论［M］.键链，译.北京：国防工业出版社，1977.

［3］ 徐彦哲.SOLAS概率破舱稳性及计算结果分析［J］.船舶标准化工程师，2014，47（1）：1-4，8. XU Yanzhe.Analysis of SOLAS probabilistic damage stability and the calculation result［J］.Ship Standardization Engineer，2014，47（1）：1-4，8.

［4］ 胡铁牛.货船概率破舱稳性计算及对分舱的影响［J］.上海交通大学学报，1997，31（11）：26-31. HU Tieniu.Probability calculation of ship damage stability and its influence on subdivision［J］.Journal of Shanghai Jiaotong University，1997，31（11）：26-31.

［5］ 户艳宏.规则波中客滚船破损横摇时域运动分析及概率破损稳性研究［D］.上海：上海交通大学，2011. HU Yanhong.Time domain roll motion of the damaged Ro-Ro passenger in beam regular waves and study of probabilistic damage stability［D］.Shanghai：Shanghai Jiao Tong University，2011.

［6］ BOULOUGOURIS E，PAPANIKOLAOU A.Advanced damaged stability assessment for surface combatants［C］//Proceeding of the 12th International Conference on the Stability of Ships and Ocean Vehicles.Glasgow，UK，2015.

［7］ HARSEN E，KRIKKE M.A probabilistic damage stability calculation method for naval ship vessels［C］// Proceedings of the 7th International Conference on Stability of Ships and Ocean Vehicles.Australia，Tasmania：STAB，2000.

［8］ BOULOUGOURIS E，PAPANIKOLAOU A.Risk-based design of naval combatants［J］.Ocean Engineering，2013，65：49-61.

［9］ BOULOUGOURIS E，PAPANIKOLAOU A.Optimisation of the survivability of naval ships by genetic algorithms［C］//Proceedings of the 3rd International Euro conference on Computer Applications and Information Technologies in the Maritime Industries（COMPIT'04）. Siguenza，Spain：［s.n.］，2004.

［10］ 胡丽芬，马坤，张凤香.破损舰船浮态稳性实时计算研究［J］.武汉理工大学学报（交通科学与工程版），2009，33（6）：1160-1163，1182. HU Lifen，MA Kun，ZHANG Fengxiang.Study on real-time calculation of stability for damaged warship［J］.Journal of Wuhan University of Technology（Transportation Science&Engineering），2009，33（6）：1160-1163，1182.

［11］ 蔡成涛，夏桂华.一种舰船破损稳性计算方法研究［J］.信息系统工程，2012（10）：133-135，130. CAI Chengtao，XIA Guihua.A study on the calculation method for damaged stability of warships［J］.Information System Engineering，2010（10）：133-135，130.

［12］ 吕振望，马坤，姜彭，等.基于提高舰船不沉性的分舱优化［J］.中国造船，2015，56（3）：108-115. LV Zhenwang，MA Kun，JIANG Peng，et al.Optimization of subdivision based on the ship's insinkability［J］.Shipbuilding of China，2015，56（3）：108-115.

［13］ 曹冬华，浦金云，熊凯军.舰艇作战系统生命力的模糊综合评估［J］.武汉理工大学学报（交通科学与工程版），2006，30（1）：110-112. CAO Donghua，PU Jinyun，XIONG Kaijun.A fuzzy comprehensive evaluation on combat system of war-ship［J］.Journal of Wuhan University of Technology（Transportation Science&Engineering），2006，30（1）：110-112.

［14］ 中国船级社.分舱与破损稳性要求实施指南：SOLAS 2009［S］.北京：人民交通出版社，2009.

［15］ 刘玉秋，聂武，王建国，等.鱼雷命中前后舰船主船体水线以下部分结构的应力分析与比较［J］.哈尔滨工程大学学报，2001，22（2）：15-19. LIU Yuqiu，NIE Wu，WANG Jianguo，et al.Stress analysis of torpedo-damaged warship structure under waterline［J］.Journal of Harbin Engineering University，2001，22（2）：15-19.

［16］ LYU Z W，MA K，LIU F.Military ship's subdivision optimization for reinforcement of anti-wind capacity after damage［J］.Journal of Marine Science and Technology，2015，20（3）：579-589.

［17］ BROWN A J，DEYBACH F.Towards a rational intact stability criteria for naval ships［J］.Naval Engineers Journal，1998，110（1）：65-77.

A probabilistic method for damage stability assessment of surface combatants

MA Kun，ZOU Mengyao，LV Zhenwang
State Key Laboratory of Structural Analysis for Industrial Equipment，School of Naval Architecture Engineering，Dalian University of Technology，Dalian 116024，China

One of the main influential factors on the survivability of a surface combatant is its vulnerability to weapon effects，which means that its damage stability determines the vulnerability of a vessel. Currently，a surface combatant's damage stability is mainly assessed via the deterministic method，which offers no comprehensive assessment compared with the probabilistic method.This paper discusses the probabilistic method of evaluating the damage stability of a surface combatant，presents a new method named‘variable interval linear interpolation’for the calculation of survival probability，and develops numerical procedures.Taking a certain combatant as an example，through calculating the damage probabilityPiand the survival probabilitySi，the subdivision index A is obtained by the sum of the product ofPiandSifor each compartment and compartment group.Research shows that，by taking the subdivision index as an evaluation index and considering the damage effects of different weapons and collisions，the probabilistic method can realize a quantitative overall assessment of a surface combatant's damage stability，thereby providing a way to increase the survivability of a combatant through the optimization of the hull subdivision in the primary stages of ship design.

surface combatants；damage stability；probabilistic method；variable interval linear interpolation

U661.2+2

A

10.3969/j.issn.1673-3185.2016.06.001

2016-04-22

时间：2016-11-18 15:19

马坤（通信作者），女，1961年生，博士，教授。研究方向：船舶破损稳性。E-mail：makun@dlut.edu.cn邹梦瑶，男，1991年生，硕士生。研究方向：船舶破损稳性。E-mail：mengyao_zou@163.com吕振望，男，1984年生，博士生。研究方向：船舶破损稳性。E-mail：lvshaoqian888@163.com

http://www.cnki.net/kcms/detail/42.1755.tj.20161118.1519.002.html 期刊网址：www.ship-research.com

马坤，邹梦瑶，吕振望.水面舰船破损稳性的概率评估方法［J］.中国舰船研究，2016，11（6）：1-7，21. MA Kun，ZOU Mengyao，LV Zhenwang.A probabilistic method fordamage stability assessmentofsurface combatant［sJ］. Chinese Journal of Ship Research，2016，11（6）：1-7，21.