基于分段动态松弛协同优化算法的船舶机舱结构优化设计

钱杨，王德禹

1上海交通大学海洋工程国家重点实验室，上海200240

2高新船舶与深海开发装备协同创新中心，上海200240

基于分段动态松弛协同优化算法的船舶机舱结构优化设计

钱杨1，2，王德禹1，2

1上海交通大学海洋工程国家重点实验室，上海200240

2高新船舶与深海开发装备协同创新中心，上海200240

基于标准的协同优化算法，针对其对初始点敏感、收敛慢等固有缺陷，将协同优化算法法与混合优化算法及动态松弛法相结合，提出分段动态松弛协同优化算法，并将其应用到船舶机舱结构多目标优化问题中。针对船舶主机舱结构静、动态多学科多目标优化问题，建立主机舱结构的多目标协同优化模型。在Isight优化软件中采用改进的分段动态松弛协同优化算法，对船舶机舱结构进行静、动态多学科多目标协同优化设计，得到优化设计的最优解。优化结果表明，相对于基于遗传算法的协同优化算法，分段动态松弛协同优化算法兼顾了优化的高效性和准确性，对于实际工程中更加复杂的多学科多目标结构优化具有一定的参考价值。

船舶机舱结构；协同优化；混合算法；动态松弛

0 引 言

为充分考虑复杂系统设计过程中各学科间的相互耦合制约特性，用以满足日益增长的设计需求，出现了多学科设计优化（Multidisciplinary Design Optimization，MDO）。MDO优化策略可以分为单级优化方法和多级优化方法，现有的单级优化方法主要包括同时运行方法（All-At-Once，AAO）、多 学 科 可 行 方 法（Multidisciplinary Feasible，MDF）和单学科可行方法（Individual Discipline Feasible，IDF）；多级优化方法主要包括协同优化（Collaborative Optimization，CO）、并行子空间优化（Concurrent subspace optimization，CSSO）和两级集成系统合成（Bi-Level Integrated System Synthesis，BLISS）。其中，协同优化算法由于采用分解建模、并行求解策略，具有建模难度低、求解效率高、模型独立性优和适于分布式计算等优点，因此是解决大规模复杂工程优化问题、多学科设计优化问题的有效方法。

协同优化作为一种新兴的优化理论方法，还存在着不少缺陷，由此引起了广泛的关注与研究。协同优化算法在系统级优化中采用的是一致性等式约束，通常情况下约束条件无法满足，会导致优化问题无法收敛。针对协同优化的这一问题，Alexandrov和Lewis［1］给出了松弛因子法，对系统级一致性等式约束进行松弛，将等式约束变为不等式形式，但因松弛因子大小取值难以确定，又成为新的难点。李响等［2］等从几何的角度出发，在松弛因子法的基础上，提出了动态松弛法，利用学科不一致信息选取松弛因子。郭健彬和曾声奎［3］将优化问题的设计空间分为3类，对每类设计空间分别赋予了不同的松弛量。

近年来，协同优化算法在复杂结构的优化设计问题中也得到了广泛应用。Balling等［4］首次采用多学科优化方法求解多目标问题，将协同优化应用到了多目标问题中。李冬琴等［5］研究了如何将多目标多学科优化问题转化为能反映设计者偏好的综合多目标问题。Jang等［6］首次将Pareto遗传算法引入到了协同优化框架中。王平等［7］将协同优化方法和多目标遗传算法应用到了车身结构优化设计中。杨丽丽等［8］提出了协同优化方法与全局多目标优化算法（CO-PE）的组合优化方法，并成功将其应用到了卫星结构优化设计中。

船舶结构具有一定的特殊性，其板厚、骨材都有规定的特殊规格，导致优化设计变量为离散变量；另船舶结构复杂，设计变量众多，学科之间通常具有相互耦合的关系。由于标准协同优化算法的一致性等式约束会导致算法收敛困难、优化设计变量的离散性会导致固定松弛方法的松弛因子难以确定，以及基于遗传算法的协同优化算法收敛缓慢等，针对机舱结构优化的实际问题，并基于以上所述已有方法的缺陷，本文拟将混合优化算法与动态松弛方法集中应用到协同优化算法中，提出分段动态松弛协同优化（Sectionalized Dynamic Relaxation Collaborative Optimization，SDRCO）算法。该算法将优化阶段分为全局搜索阶段和局部搜索阶段，分段优化过程兼顾整个优化过程的稳定性和高效性。在全局阶段和局部阶段都采用动态松弛法，但减小局部阶段的松弛系数，以缩小系统级与学科级之间的差异，保证最终优化结果的准确性。并将以某船机舱结构为例，分别采用所提出的SDRCO算法与基于遗传算法的协同优化算法（Collaborative optimization algorithm based on genetic algorithm，GA-CO）对其进行优化设计，通过对这2种方法优化结果的比较分析，验证SDRCO算法的高效性与准确性。

1 协同优化算法的改进

1.1 标准协同优化算法

协同优化算法是多学科设计优化方法中重要的多级优化算法，其可将复杂的工程系统设计问题根据具体的工程分工形式，分解成系统级和学科级两级优化结构。学科级的优化目标是根据学科内约束条件，使学科级的优化方案与系统级优化方案之间差异最小。系统级的优化目标是使整个优化问题的目标最优，并通过等式约束条件保证各个子学科间耦合变量的一致性。标准协同优化数学模型如下。

1）系统级优化。

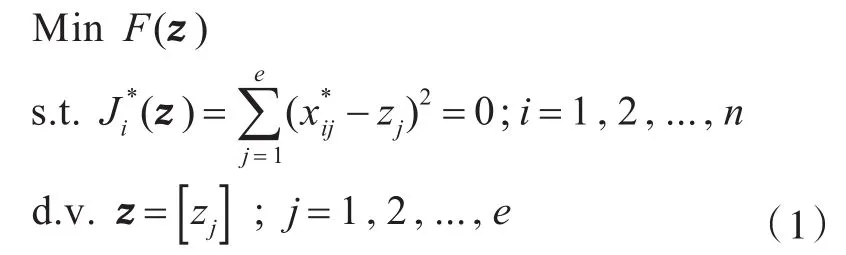
2）学科级优化。

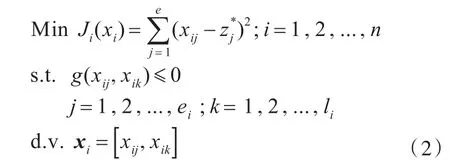
协同优化算法的优点在于，对于复杂的大型工程问题，不需要进行系统分析就可以处理学科间的耦合问题。但协同优化算法由于本身结构的原因，也存在着一些弊端，如协同优化算法的一致性约束形式会大大缩减优化搜索空间，使优化收敛较慢甚至是不收敛，或者收敛到局部解。为了改善算法性能，结合船舶结构优化的实际问题，本文采用以下措施对标准协同优化进行改进。

1.2 分段动态松弛协同优化（SDRCO）算法

针对标准协同算法的弊端，现做出如下改进。

1）为解决协同优化收敛困难，并易收敛到局部最优解的问题，采用混合优化策略，将整个优化搜索过程分为2个优化阶段：全局优化阶段和局部优化阶段。在全局优化阶段，系统级优化属多目标优化问题，所以系统级优化采用多目标智能优化算法非支配排序遗传算法Ⅱ（NSGA-Ⅱ），学科级优化属单目标优化问题，所以学科级优化采用单目标优化算法多岛遗传算法（MIGA），这样可以从算法上在整个搜索空间进行优化搜索，避免优化陷入局部最优。经过全局优化之后，当收敛到达全局最优解附近时，进入局部优化搜索阶段。系统级采用直接搜索方法Hooke-Jeeves算法，学科级采用多岛遗传算法（MIGA），这样可以加快优化收敛速度，更快地达到最优解。因为局部优化阶段采用的是单目标的直接搜索方法，所以全局搜索结束后得到的是Pareto集，需要根据实际优化问题对2个目标函数（质量、加速度）取合适的权重，从而得到需要的最优解及对应的设计点，并将此作为局部优化搜索的起始点进行优化，最终得到最优解。

2）由于船舶结构的板材都有特殊的规格，因此板材厚度建议取整数，而骨材尺寸也有规范规定统一的尺寸规格，一般也取整数值。但这样会导致船舶结构优化设计变量的取值都是固定孤立的整数值，从而成为离散变量，在采用标准协同优化一致性约束时会出现约束过强的问题，而采用固定不等式松弛因子时，确定最佳松弛因子的大小又相对困难，所以本文采用李响等［9］基于超半球子空间思想的动态松弛法。以两学科问题为例，设在某次迭代过程中经过第一学科优化后得到最优设计点X1，经过第二学科优化后得到最优设计点X2，定义

式中，Δ 表示两学科间的不一致信息。

令

式中，0.5≤λ≤1。那么，新的系统级约束转化为

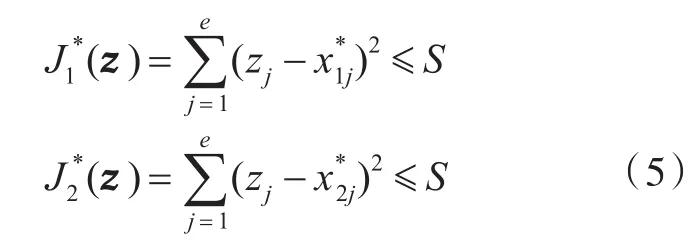
式（3）表示的是分别以 X1和X2为中心、S为半径的2个高维空间里的球，系统级优化的可行域为这2个球的相交部分。随着迭代的进行，学科间的不一致信息量Δ不断减小，致使S也在动态变化。动态松弛方法可以有效克服由系统级一致性等式约束带来的求解困难，在每一步迭代步中，不仅能保证系统级优化问题是可行的，还能兼顾学科间的一致性要求。

本文在采用动态松弛方法时，会根据优化阶段的不同，调整动态松弛方法不一致信息的定义。在全局优化阶段，因为需要在整个空间进行全局搜索，避免优化陷入局部最优，故令λ值取最大值1，这样可以使搜索空间尽可能扩大，避免优化陷入局部解。在局部优化阶段，因为经过全局阶段的优化过程后得到的解集已经在最优解的附近，为了缩小学科级与系统级之间的差异，保证多学科之间的耦合性，使优化结果更加准确，可适当减小λ值，本文取λ=0.7。

在对标准协同优化算法做出上述改进措施之后，得到了改进之后的SDRCO算法，算法核心步骤示意图如图1所示。

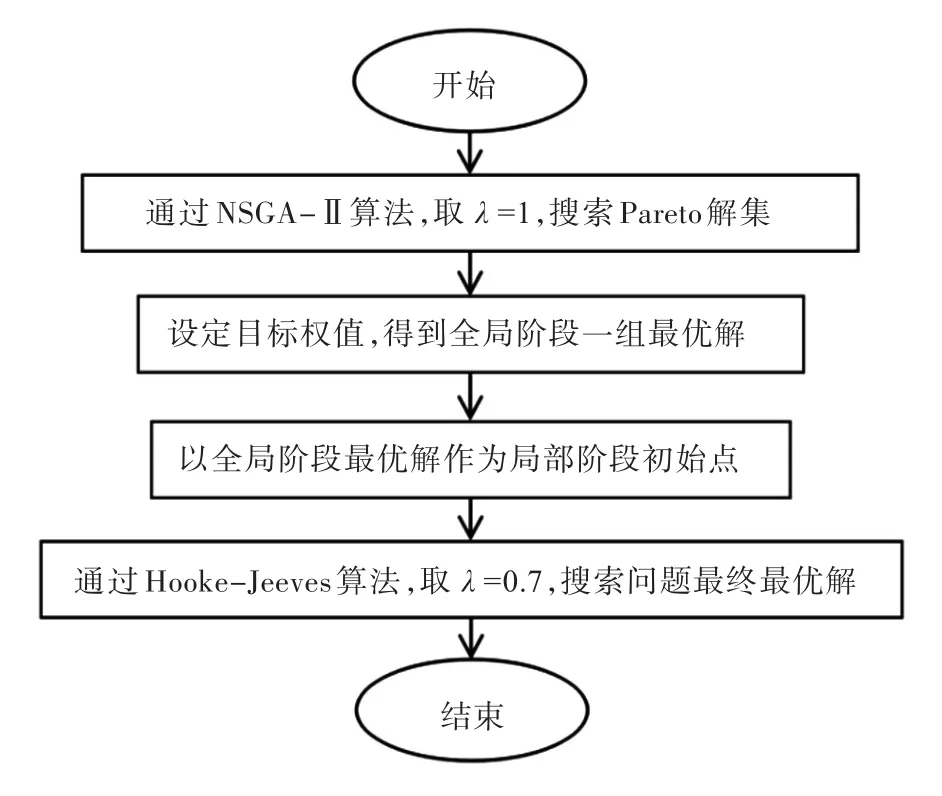
图1 SDRCO算法核心步骤Fig.1 The core steps of SDRCO algorithm

2 船舶主机舱结构多目标协同优化

将改进之后的协同优化算法应用到某船的主机舱结构多学科多目标优化问题中，并对比SDRCO算法与GA-CO算法的优化结果。

2.1 优化数学模型

优化结构为某实船机舱立体舱段模型。船长方向的长度为18 m，船宽方向的宽度为16.4 m，高度为7.8 m，包括双层底、中间平台、甲板、舷侧、纵舱壁、横舱壁等结构，主机、齿轮箱和其他附加设备以质量点和MPC的形式安装在内底板上。分别对主机舱有限元模型进行静力与动力分析。在进行机舱固有频率和响应计算时，结构附连水质量以Patran软件自带的功能虚拟质量法的方式加到与水接触的外底板单元上。机舱在某一静载荷作用下，出现最大正应力σmax=227 MPa，最大剪应力为τmax=112 MPa；在主机位置施加主机激励力，得到机舱机构最大位移响应值dmax=0.054 8 mm，最大速度响应值vmax=2.96 mm/s，最大加速度响应值amax=159 mm/s2；进行模态计算，得到机舱固有一阶频率 f1=9.27 Hz。

1）设计变量。

在机舱有限元模型中，分布着36种板材与11种骨材。将每一种骨材的面板宽w、腹板高h、面板厚t1及腹板厚t2分离成4个设计参数，共计44个骨材设计参数，每种板材厚度t计为一个设计参数，共计36个板材设计参数，总计80个设计参数。分别将所有的设计变量对质量、固有频率、正应力、剪应力、位移、速度、加速度等响应值进行灵敏度分析［10］。根据灵敏度分析结果，显示主要板材厚度以及主要骨材腹板高度会对结构力学性能产生较大影响，因此，从80个设计参数中选出了17个参数作为优化设计变量，其中 x1～x13为主要板材厚度，x14～x17为主要骨材腹板高度。

2）约束条件。

在系统级优化中，以一致性约束J1和J2作为约束条件；在静力学学科优化中，以最大正应力σmax与最大剪应力τmax作为约束条件；在动力学学科优化中，以一阶固有频率 f1、最大位移响应值dmax及最大速度响应值vmax作为约束条件。

3）目标函数。

系统级优化中，在全局优化阶段，以结构质量m和最大加速度响应值amax作为多目标函数；在局部优化阶段，以全局优化结果为基础确定2个目标函数的权重，然后以加权值作为局部阶段的目标函数，本文取机舱结构质量m的权系数为0.35，加速度响应 amax最大值的权系数为0.65。在静力学与动力学学科级优化中，分别以一致性约束J1和J2作为目标函数。

根据上述描述，采用SDRCO算法建立主机舱结构多学科多目标协同优化的数学模型如下。

系统级：

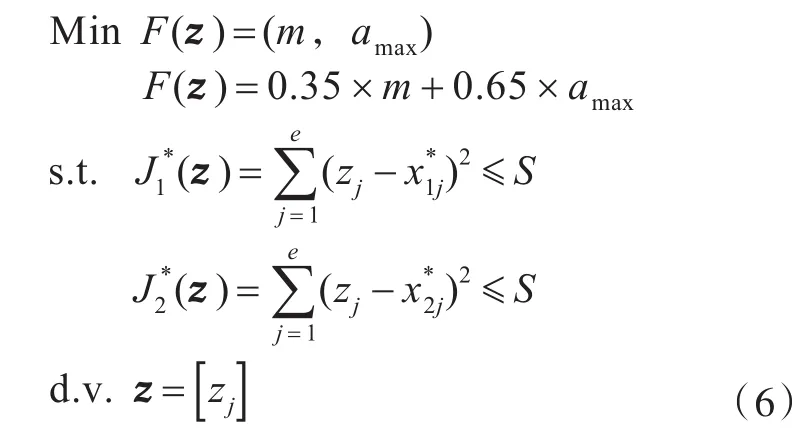
静力学学科：

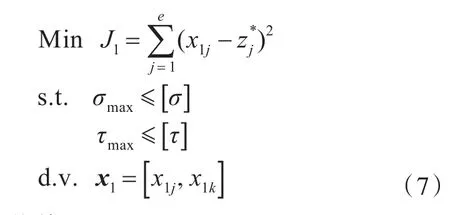
动力学学科：

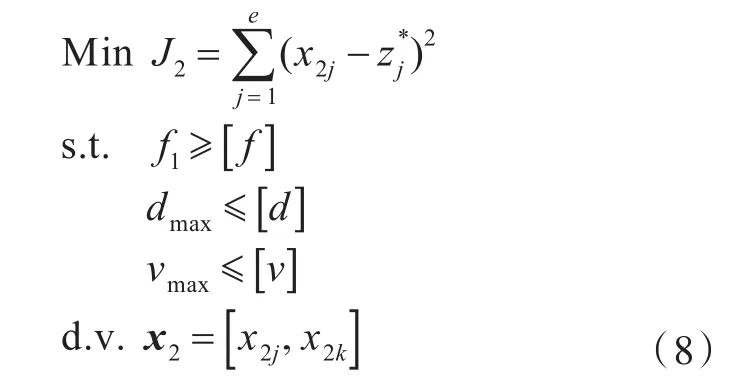
2.2 协同优化流程

本文采用优化软件Isight集成前处理软件Patran和有限元计算软件Nastran进行迭代计算。由于机舱有限元模型较复杂，特别是在进行频响计算时耗时较长，影响优化效率，故本文采用径向

基函数近似模型代替有限元计算过程，以此来提高优化效率。径向基函数是一类以待测点与样本点之间的欧式距离为自变量的函数。通过采用欧氏距离，径向基函数可以很容易地把一个多维问题转化为以欧氏距离为自变量的一维问题。

首先，采用超拉丁试验设计方法进行设计变量敏感度分析，选出设计变量；然后，用超拉丁试验设计方法采集样本点，建立近似模型；最后，建立协同优化结构，在全局搜索阶段采用非支配排序遗传算法（NSGA-Ⅱ）进行全局搜索，直到设计点到达最优解附近，然后根据优化需要确定权重，找到一组最优解及其对应的设计点，并以此设计点为局部搜索阶段的起始点，之后采用Hooke-Jeeves算法进行局部搜索，最终找到优化设计最优解。采用SDRCO算法，机舱结构多目标协同优化的流程如图2所示。

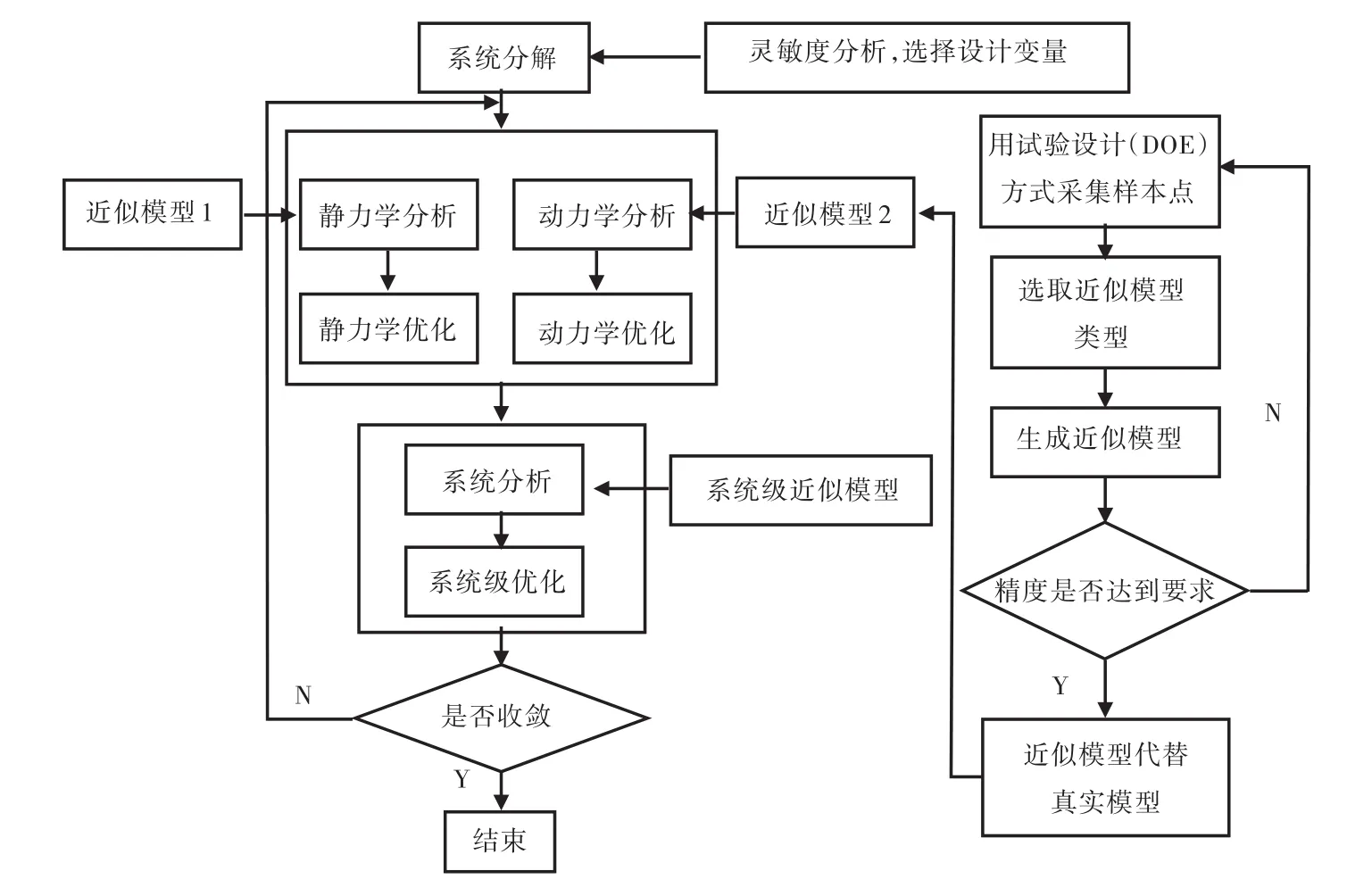
图2 基于SDRCO算法的机舱结构优化流程图Fig.2 Flow chart of the engine room structure optimization based on SDRCO algorithm

2.3 优化结果比较

分别采用SDRCO算法和GA-CO算法对该船主机舱结构进行多目标优化。采用SDRCO算法时，在全局优化结束并得到Pareto解集之后，根据确定的权重系数得到一组解，并以此优化结果作为局部优化阶段的初始设计变量进行优化，得到最终最优解。然后，与基于遗传算法的协同优化算法得到的最优解进行比较分析。

基于SDRCO算法，在全局优化阶段得到的Pareto解集如图3所示，局部优化阶段的迭代过程如图4所示。

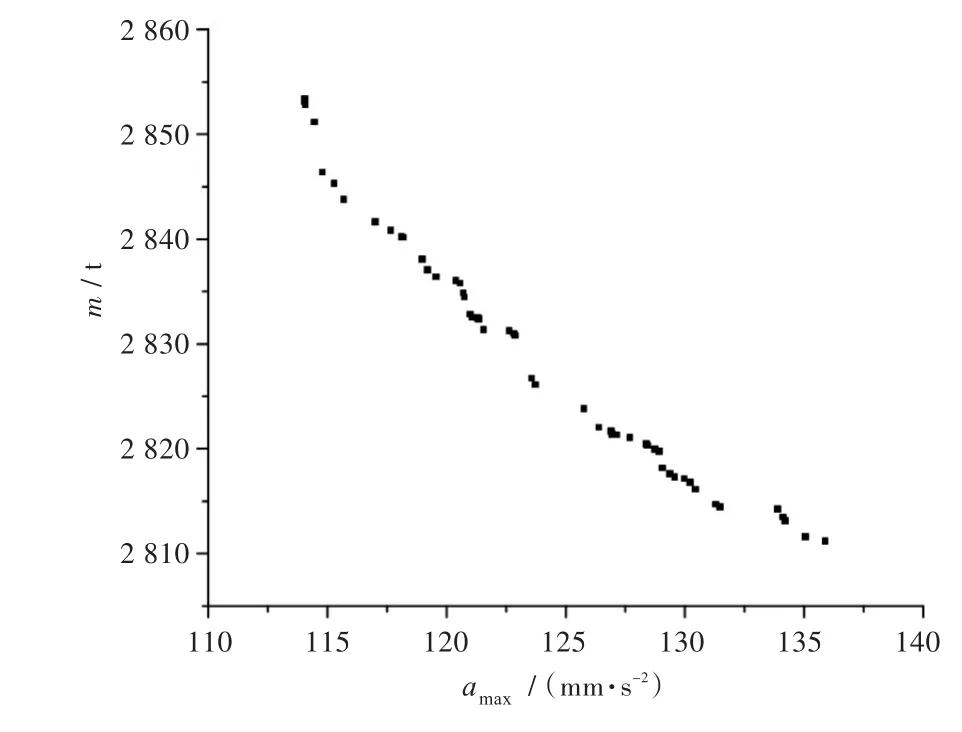
图3 SDRCO算法全局优化Pareto解集Fig.3 Pareto solution set in the global optimization phase based on SDRCO algorithm

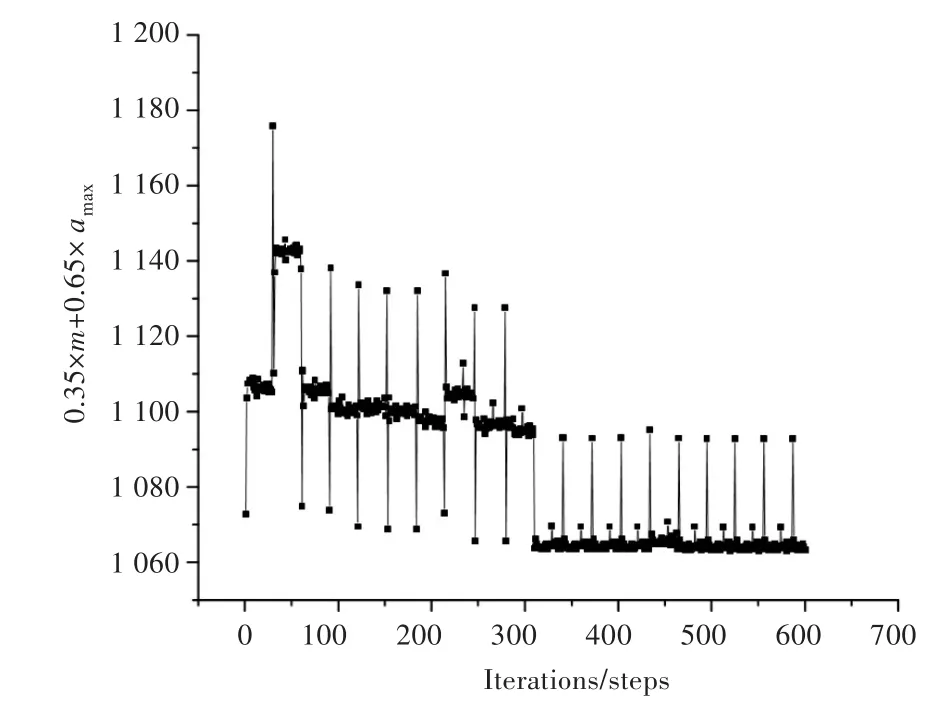
图4 SDRCO算法局部优化迭代过程Fig.4 Iterative process in the partial optimization phase based on SDRCO algorithm

基于GA-CO算法优化Pareto解集，如图5所示。

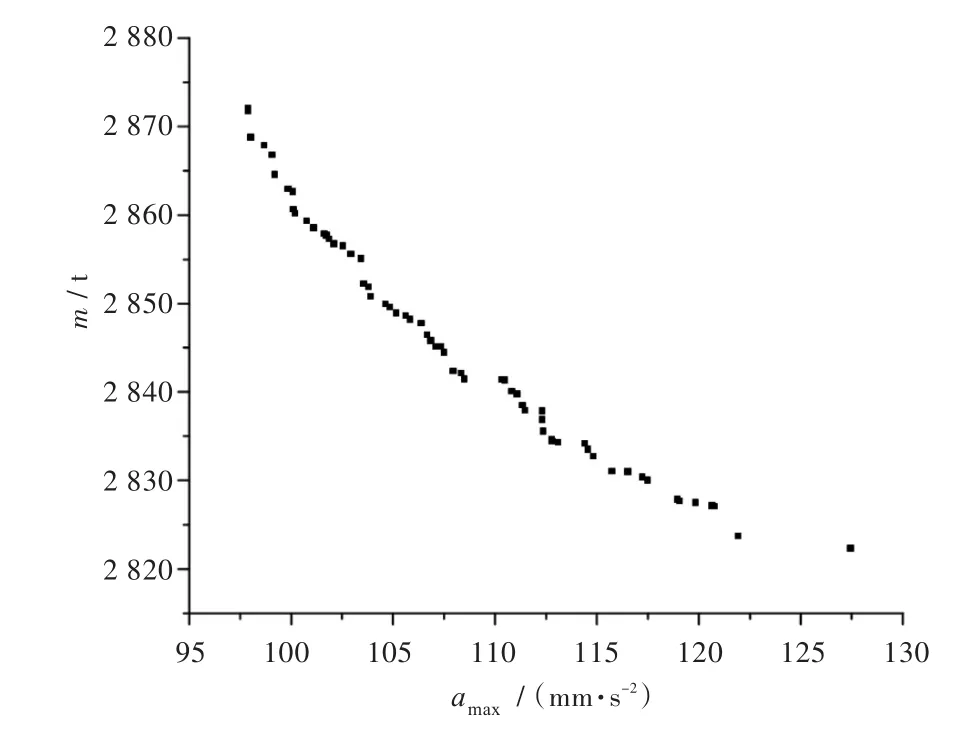
图5 GA-CO算法优化Pareto解集Fig.5 Pareto solution set optimized by GA-CO algorithm

将2种算法获得的优化前后静、动力学响应最优解以及设计变量取值汇总于表1与表2。

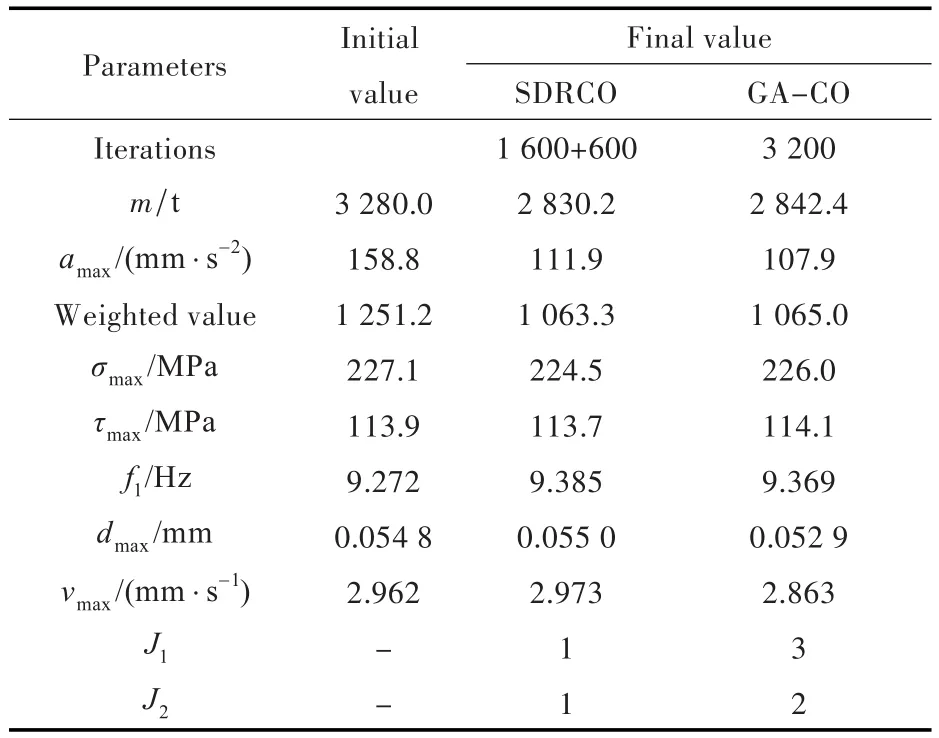
表1 SDRCO算法与GA-CO算法的优化结果对比Tab.1 The comparison between results based on SDRCO algorithm and GA-CO algorithm

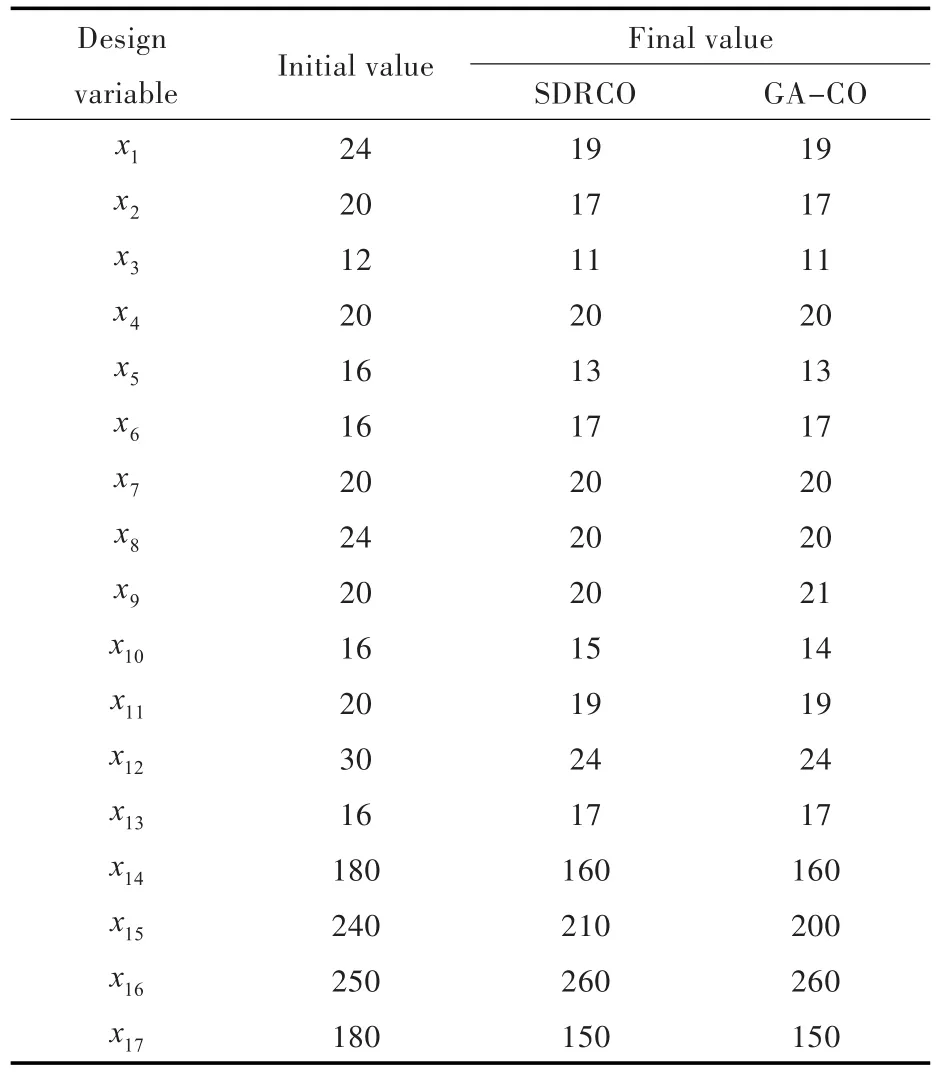
表2 SDRCO算法与GA-CO算法的设计变量对比Tab.2 The comparison of design variables between SDRCO algorithm and GA-CO algorithm

根据2种算法的优化结果对比分析，可以得出如下结论：

1）从优化结果可以看出，采用本文提出的SDRCO方法进行优化，经过2段总计2 200次迭代之后，得到2个优化目标值：结构质量优化到了2 830.2 t，和初始值相比减小了约13.7%；最大加速度降低到了111.9 mm/s2，和初始值相比减小了29.6%，优化效果明显。

2）通过将本文的SDRCO算法与GA-CO算法的优化结果进行比较分析可以看出，本文方法通过全局1 600次、局部600次，总计2 200次迭代得到的最优解，和全程采用GA-CO算法相比其优化次数减少了1 000次，最终得到的最优解更小，说明了本文采用分段优化方法的高效性。

3）SDRCO算法采用分段动态松弛，在局部优化阶段缩小了动态松弛因子，减小了系统级与学科级之间的差异性。从优化结果可以看出，2个子学科与系统级之间的差异分别为1和1，和GA-CO算法相比差异性更小，保证了优化结果的准确性。

3 结 语

本文考虑到标准协同优化算法收敛困难、易陷入局部最优解等固有缺陷以及船舶结构优化实际问题的特殊性，针对标准协同优化做出了2点改进：一是采用混合优化算法，将优化问题分为全局与局部2部分，在全局阶段采用全局多目标优化方法保证收敛性，在局部阶段采用直接搜索方法加快收敛，提高算法的稳定性；二是采用分段动态松弛法代替一致性约束和固定松弛因子法，在全局阶段动态松弛因子取最大值以避免陷入局部最优解，在局部阶段缩小松弛因子以保证结果的准确性，得到了改进之后的SDRCO算法。利用该方法，对某船主机机舱结构进行了多学科多目标优化。首先，采用SDRCO算法进行优化后，发现2个优化目标结构的质量与加速度都有大幅的下降，优化效果明显，说明方法有效；其次，将本文提出的SDRCO方法与已有的GA-CO算法相比，发现采用SDRCO算法不仅迭代次数更少，优化结果还更好，验证了算法的高效性；再次，通过采用分段动态松弛，SDRCO算法局部优化阶段系统级与

学科级之间的差异更小，说明SDRCO算法具有更强的准确性。可见，SDRCO方法对于实际工程中复杂船舶结构的多学科多目标优化问题具有较好的适用性。

［1］ ALEXANDROV N M，LEWIS R M.Analytical and computational aspects of collaborative optimization for multidisciplinary design［J］.AIAA Journal，2002，40（2）：301-309.

［2］ 李响，李为吉.利用协同优化方法实现复杂系统分解并行设计优化［J］.宇航学报，2004，25（3）：300-304. LI Xiang，LI Weiji.A new collaborative optimization algorithm and its applications to complex system parallel design［J］.Journal of Astronautics，2004，25（3）：300-304.

［3］ 郭健彬，曾声奎.自适应协同优化方法研究［J］.系统工程与电子技术，2009，31（5）：1108-1112. GUO Jianbin，ZENG Shengkui.Research on adaptive collaborative optimization method［J］.System Engineering and Electronics，2009，31（5）：1108-1112.

［4］ BALLING R J，WILKISON C A.Execution of multidisciplinary design optimization approaches on common test problems［J］.AIAA Journal，1997，35（1）：178-186.

［5］ 李冬琴，蒋志勇，杨永祥.基于自适应加权的船舶多目标协同优化［J］.中国造船，2012（4）：75-83. LI Dongqin，JIANG Zhiyong，YANG Yongxiang.Multidisciplinary and multi-objective design optimization based on adaptive weighted-sum method［J］.Shipbuilding of China，2012（4）：75-83.

［6］ JANG B S，YANG Y S，JUNG H S，et al.Managing approximation models in collaborative optimization［J］. Structural and Multidisciplinary Optimization，2005，30（1）：11-26.

［7］ 王平，郑松林，吴光强.基于协同优化和多目标遗传算法的车身结构多学科优化设计［J］.机械工程学报，2011，47（2）：102-108. WANG Ping，ZHENG Songlin，WU Guangqiang.Multidisciplinary design optimization of vehicle body structure based on collaborative optimization and multi-objective genetic algorithm［J］.Journal of Mechanical Engineering，2011，47（2）：102-108.

［8］ 杨丽丽，陈昌亚，王德禹.基于多目标协同优化算法的卫星结构优化设计［J］.上海交通大学学报，2014，48（10）：1446-1450. YANG Lili，CHEN Changya，WANG Deyu.Structural optimization of satellite based on multi-objective collaborative optimization algorithm［J］.Journal of Shanghai Jiaotong University，2014，48（10）：1446-1450.

［9］ 李响，李为吉.基于超球近似子空间的协同优化方法及应用研究［J］.西北工业大学学报，2003，21（4）：461-464. LI Xiang，LI Weiji.Collaborative optimization based on inter-disciplinary inconsistency information and its application to mechanical system design［J］.Journal of Northwestern Polytechnical University，2003，21（4）：461-464.

［10］ 黄海燕，王德禹.基于灵敏度多学科优化设计变量的模糊分析［J］.上海交通大学学报，2009，43（8）：1327-1331. HUANG Haiyan，WANG Deyu.Fuzzy comprehensive analysis of design variables for multidisciplinary design optimization based on sensitivity analysis［J］. Journal of Shanghai Jiaotong University，2009，43（8）：1327-1331.

Optimization design of ship engine room structures based on sectionalized dynamic relaxation collaborative optimization method

QIAN Yang1，2，WANG Deyu1，2

1 State Key Laboratory of Ocean Engineering，Shanghai Jiao Tong University，Shanghai 200240，China

2 Collaborative Innovation Center for Advanced Ship and Deep-Sea Exploration，Shanghai 200240，China

Based on the standard collaborative optimization and aiming at its inherent flaws such as high sensitivity to the initial guess and slow convergence,this paper combines the collaborative optimization algorithm,the hybrid optimization algorithm,and the dynamic relaxation method to put forward a sectionalized dynamic relaxation collaborative optimization algorithm.The proposed algorithm can be applied in the multi-objective optimization of ship engine room stuctures.Meanwhile,the multi-objective collaborative optimization model of the main ship engine room is established to solve the static and dynamic,multidisciplinary and multi-objective optimization of ship engine room structures.Then,the collaborative optimization is validated through the Isight software to draw the optimal solution.It is shown that the step-by-step dynamic relaxation collaborative optimization algorithm achieves both accuracy and efficiency compared with that based on the genetic algorithm,which provides great

to the multidisciplinary and multi-objective design optimization of more complex structures in real projects.

ship engine room structure；collaborative optimization；hybrid algorithm；dynamic relaxation

U663

A

10.3969/j.issn.1673-3185.2016.06.007

2016-04-06

时间：2016-11-18 15:19

教育部、财政部基金资助项目（201335）

钱杨，男，1992年生，硕士生。研究方向：船体结构优化设计理论与方法。E-mail：1175968402@qq.com王德禹（通信作者），男，1963年生，博士，教授，博士生导师。研究方向：结构动力学和计算结构力学。E-mail：dywang@sjtu.edu.cn

http://www.cnki.net/kcms/detail/42.1755.tj.20161118.1519.014.html 期刊网址：www.ship-research.com

钱杨，王德禹.基于分段动态松弛协同优化算法的船舶机舱结构优化设计［J］.中国舰船研究，2016，11（6）：40-46. QIAN Yang，WANG Deyu.Optimization design of ship engine room structures based on sectionalized dynamic relaxation collaborative optimization method［J］.Chinese Journal of Ship Research，2016，11（6）：40-46.