非全周开口滑阀运动过程液动力数值计算
王建森, 刘耀林, 冀 宏, 王鹏飞
(兰州理工大学 甘肃省流体机械及系统重点实验室,甘肃 兰州 730050)
非全周开口滑阀运动过程液动力数值计算
王建森, 刘耀林, 冀 宏, 王鹏飞
(兰州理工大学 甘肃省流体机械及系统重点实验室,甘肃 兰州 730050)
为了获取非全周开口滑阀运动过程液动力特性,以油液流出U形节流槽方向为例,采用非一致性、滑移网格技术及UDF编程方法,研究阀芯运动速度、运动方向、进出口压差及节流槽个数对阀芯所受液动力的影响规律.研究结果表明,在阀芯运动速度低于0.1 m/s,阀芯运动时所受的液动力与阀口开度一定稳态计算时的液动力相差不大,可以用瞬态计算近似稳态计算;阀芯运动速度越高,阀芯所受液动力与稳态计算时液动力偏离越大;当阀芯运动方向改变时,液动力出现滞环,速度越大,滞环越大且在小开口下出现液动力方向变化;进出口压差越大,节流槽个数越多,阀芯所受液动力增大,滞环越明显.
滑阀;非全周开口;液动力;阀芯运动
非全周开口滑阀是液压控制阀的基本结构形式之一,典型结构特征为在阀芯凸肩圆周方向均布有大小、形状不同的沟槽,如U形、V形、K形、球形等,通过槽形几何尺寸的改变和不同沟槽的组合可以得到不同的阀芯位移通流面积曲线,从而可以获得丰富多变的流量控制特性,因此在比例控制阀技术中得到广泛使用.液动力是液压阀阀芯驱动装置设计时必须考虑的基本要素之一.由于非全周开口滑阀阀口的几何构造复杂,在不同的阀口开度下存在阀口迁移、流束射流角变化大等因素,传统的全周开口滑阀液动力理论计算公式不再适用于非全周开口滑阀液动力计算.
冀宏等[1-7]采用计算流体动力学(CFD)方法获取非全周开口滑阀的液动力特性,该研究的不足之处在于工作主要集中在阀口开度一定下的稳态计算,只能获得有限阀口开度下液动力的离散分布图,且未考虑实际工况中阀芯瞬态运动对阀芯所受液动力的影响.由于阀芯瞬态运动时液动力试验测试的困难性,目前研究手段以数值计算方法为主,DEL Vescovo等[8]建立了方向控制阀二维计算域模型,采用动网格技术对3种工况条件即进出口压力恒定,阀芯开启运动;阀口开度固定,进口压力脉动;进口压力阻尼振荡,阀芯开启运动下液流由阀腔流向油道时阀的流量特性和液动力特性进行数值模拟研究;赵蕾等[9]建立方向控制阀三维计算域模型,同样采用动网格技术对2种工况条件即流量恒定,阀芯运动速度不同;阀芯运动速度恒定,流量不同下液流由油道流向阀腔时阀的流量特性和液动力特性进行模拟分析;Posa等[10]采用浸没边界技术(immersed-boundary technology)的直接数值模拟方法,就全周开口滑阀阀芯运动速度对滑阀性能的影响进行数值研究.以上研究表明,全周开口滑阀阀芯瞬态运动对阀的内部流场结构、外部流量特性及液动力特性均有重要影响.
有关非全周开口滑阀阀芯瞬态运动对阀芯液动力特性的影响规律尚不清楚,鲜见文献报道.本文以阀芯凸肩圆周布置有对称单U形槽的非全周开口滑阀为例,分别就阀芯运动速度、运动方向、进出口压差及节流槽个数对阀芯所受液动力的影响规律进行初步探讨.
1 几何模型及计算方法
如图1(a)所示为研究的非全周开口滑阀结构尺寸简图[11],在阀芯凸肩沿圆周方向上均布有U形节流槽.
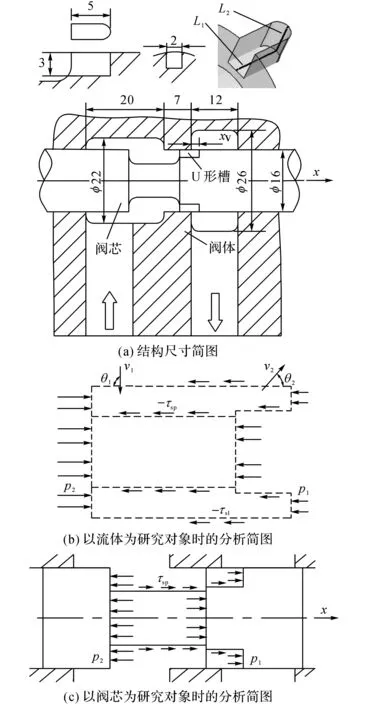
图1 非全周开口滑阀结构简图Fig.1 Structure diagram of non-circular opening spool valve
当油液流经阀腔时,由于流速的大小和方向发生变化,会产生一个作用于阀芯上的轴向液动力.通常有两种方法来求取该液动力.一种方法是以流体为研究对象,取控制体如图1(b)所示,利用动量定理求取作用在控制体上x轴方向上的外力矢量和,即
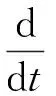
式中:F为作用在阀芯上的液动力;τsl、A1为阀体对控制体的黏性切应力和作用面积;ρ为油液的密度;v、vx、n分别为油液流入或流出控制体的流速及在x轴方向上速度分量和单位法向量;f为作用在控制体上单位质量的体积力.若忽略作用在控制体上的体积力,则作用在阀芯上的轴向液动力为

等号右边前两项为稳态液动力,第3项为瞬态液动力.该方法需要预先知道液体流入、流出控制体的流速和射流角,王东升[11]给出阀口开度一定稳态下非全周开口滑阀液动力近似计算公式,但不适用于阀芯运动状态下液动力的计算.
另一种方法是以阀芯为研究对象,通过流场解析获得阀腔内压力分布后,对受力面积积分求取作用在阀芯壁面上的液压力,如图1(c)所示.
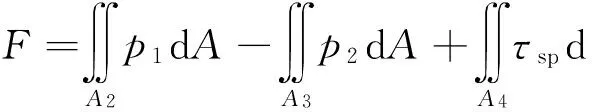
式中:p1、A2分别为作用在阀芯右侧凸肩上的液压力和承压面积,p2、A3分别为作用在阀芯左侧凸肩上的液压力和承压面积,τsp、A4分别为作用在阀芯阀杆上的黏性切应力和作用面积.该方法直观、易于理解,可以用于任意复杂阀口结构下液动力的计算问题.
采用第2种方法,利用Fluent软件二次开发UDF编程功能,通过3个用户自定义函数DEFINE_ADJUST、DEFINE_ZONE_MOTION、DEFINE_EXCUTE_AT_END分别经调用Compute_Force_And_Moment函数实现液压力计算、阀芯运动定义及最终计算数据文件的输出存储等功能,经编译加载勾选后实现与软件求解器动态数据通讯.
2 网格划分及模型验证
以图1所示的结构尺寸创建非全周开口滑阀流动区域三维模型为例,流动域分为进油腔、回油腔和阀腔3个体进行网格划分.采用四面体结构,节流槽处网格加密,定义流动域间交界面为Interface滑移网格界面,网格划分如图2所示.
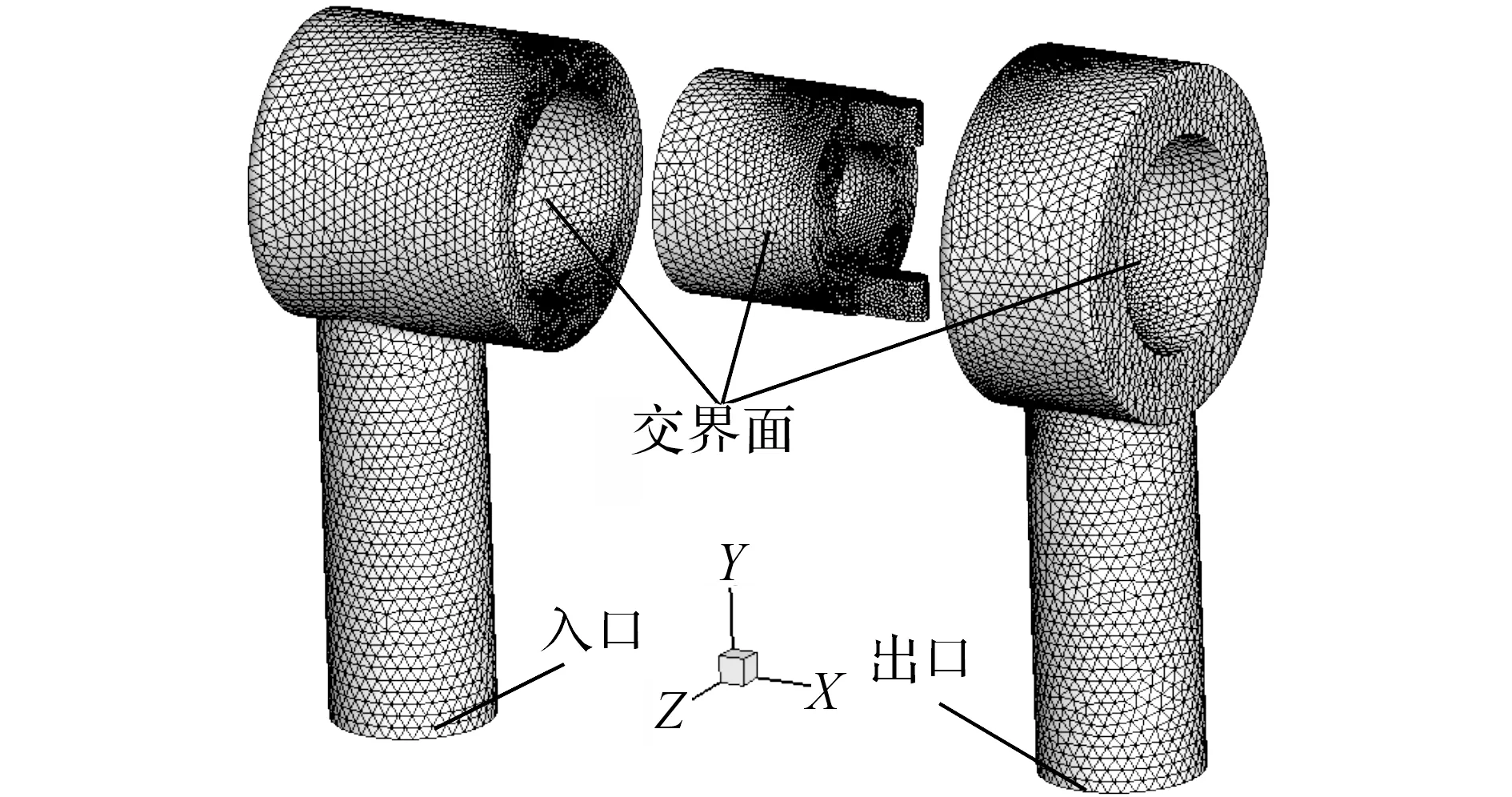
图2 非全周开口滑阀流场计算域网格Fig.2 Grid diagram of non-circular opening spool valve
以油液流出U形节流槽方向为例,边界条件设置与文献[11]的试验条件一致,即入口边界、出口边界为试验设定压力.为了抑制阀口空化流动的影响,将回油背压设定为2 MPa,可用单相流模型进行模拟.阀内流动采用RNGk-ε湍流模型,标准壁面函数,模型常数设为系统默认值,油液密度ρ为860 kg/m3,运动黏度ν为4×10-5m2/s.不同阀口开度xv下稳态计算所得阀芯所受液动力F及体积流量qV与试验测试数据的对比,如图3所示.图中,下标t、s分别表示试验值及稳态值,负号表示液动力方向为使阀口关小方向.由图3可见,数值模拟结果与试验数据吻合较好,故模型可用.

图3 液动力及流量稳态数值计算与试验数据对比图Fig.3 Comparison of steady calculation and test data
3 计算结果及分析
3.1 阀芯运动速度的影响
普通液压阀阀芯典型运动速度约为0.1m/s[8,12],具有高动态性能的开关阀和比例阀阀芯典型运动速度约为1 m/s[8],故分别在阀芯静止、阀芯以这两种速度匀速开启时,在相同进、出油口压差情况下仿真计算,得到阀芯所受的液动力对比,如图4所示.

图4 不同阀芯运动速度下的液动力曲线Fig.4 Flow force curves in different valve movement speed
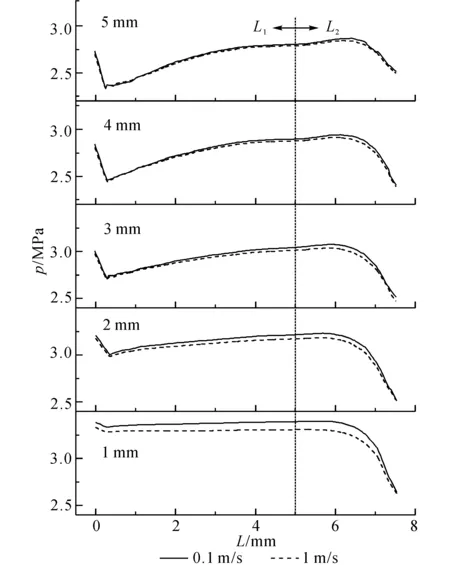
图5 压差为1.5 MPa、不同阀芯运动速度下节流槽壁面“L”折线上压力分布图Fig.5 Pressure profile of line “L” in notches with different valve speed under differential pressure is 1.5 MPa
由图4可见,在进、出口压差一定,阀芯沿开启方向运动时,阀芯运动速度越快,阀芯所受液动力越大,液动力方向沿x负方向,在小阀口开度下阀芯运动速度对液动力的影响比大阀口开度下显著,液动力的变化梯度随阀口开度的增大而变小.这可由图5两种阀芯运动速度下节流槽底部中截面节流槽壁面“L”折线上的压力分布对比图得到解释.压力采样位置如图1(a)所示,“L”形折线为节流槽中截面与槽壁面交线,L1沿轴向方向,L2沿径向方向.由图5可见,阀芯运动速度增大使得节流槽壁面L2处的压力分布降低,故作用在阀芯右侧凸肩上使阀芯开启的力减小,而总的合力使阀口关闭的力增大;该压力分布在阀口开度小时差别大,阀口开度大时差别小,使得液动力在阀口开度小时比在阀口开度大时变化明显;由图4可见,当阀芯以0.1 m/s速度开启时,通过瞬态计算所得的液动力与稳态计算所得的液动力差别不大,故可以用瞬态计算近似稳态计算,得到连续的液动力变化曲线并可以避免稳态计算时网格重复划分的繁琐过程.
3.2 阀芯运动方向的影响
当进、出口压差为1.5 MPa时,阀芯分别以两种典型运动速度匀速开启和关闭下进行仿真计算,得到阀芯所受液动力的对比图,如图6所示.
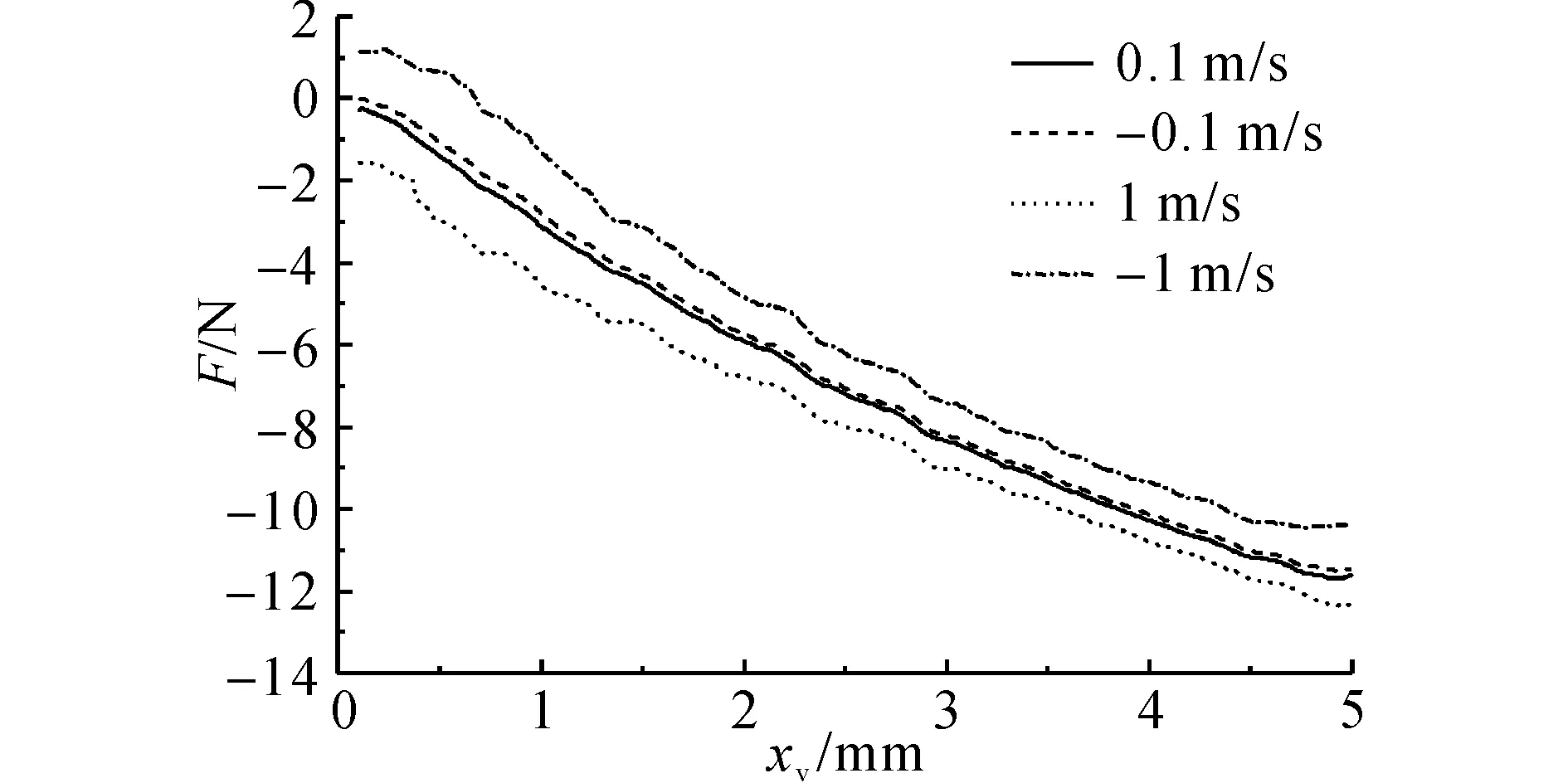
图6 阀芯运动方向改变时的液动力曲线Fig.6 Flow force curves in different valve movementdirection
由图6可见,当阀芯运动方向改变时,阀芯所受的液动力出现滞环现象,运动速度越大,滞环越大,且当阀芯运动速度达-1 m/s时,在阀口小开度下出现液动力方向变化,即产生一个驱使阀芯开启的液动力,这意味着阀芯在小开度下高速往复运动时有可能出现自激振荡现象.如图7所示为阀芯以1 m/s速度匀速开启和关闭时节流槽中截面与槽底相截“L”形折线上压力分布进行对比.由图7可见,阀芯以同样速度开关运动时在节流槽壁面L2处的压力分布不重合,出现滞环,在同一阀口开度位置关闭运动时节流槽壁面的压力分布比开启运动时的压力分布高,从而造成液动力出现滞环;在高速关闭运动小阀口开度位置时节流槽壁面L2处的压力升高较大,可能为阀芯与节流槽内液流相向运动,加剧了射流动量变化的缘故,使得液动力方向发生变化.
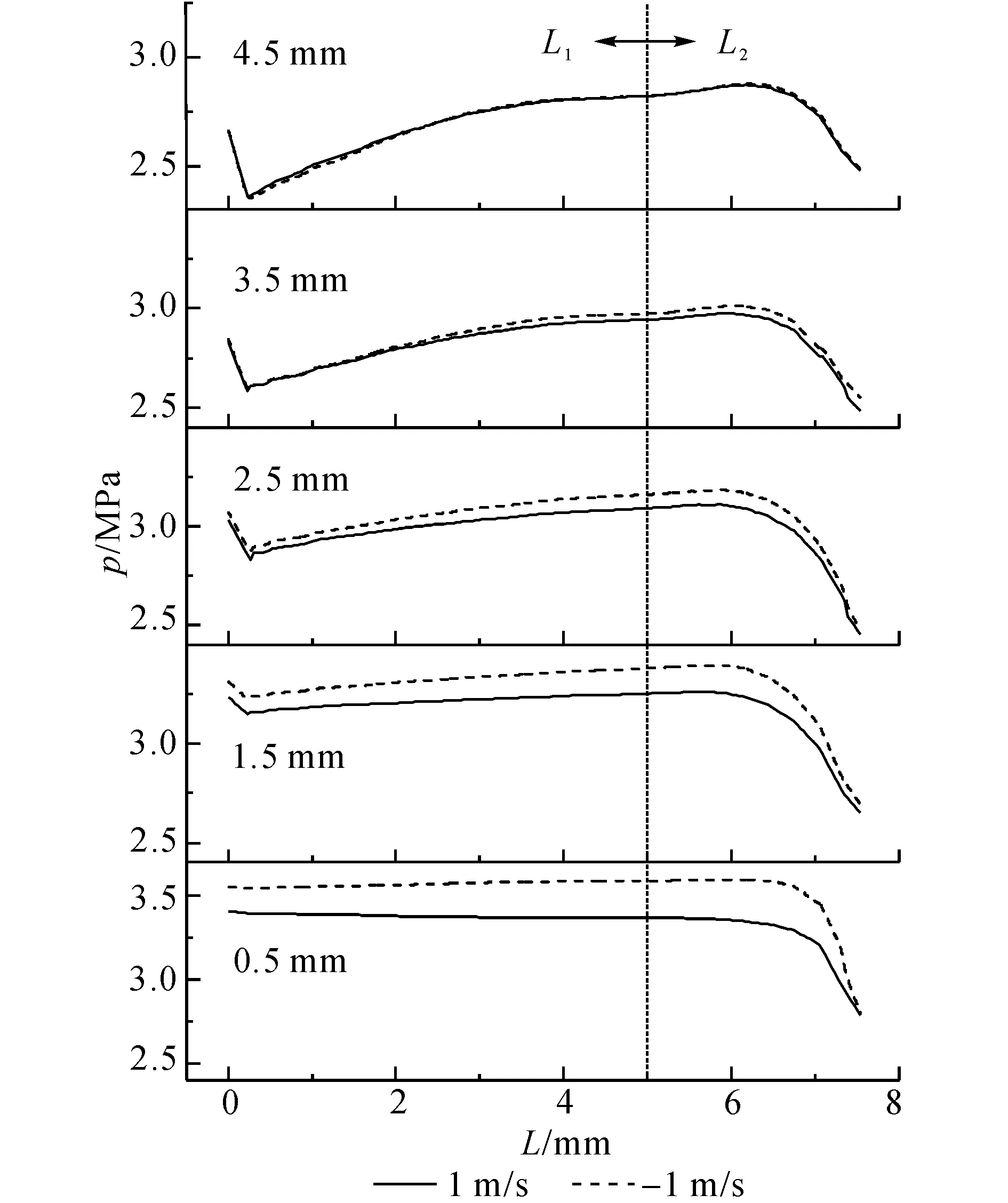
图7 压差为1.5 MPa阀芯启闭运动时节流槽底“L”折线上压力分布图Fig.7 Pressure profile of line “L” in notches with different valve moment direction under 1.5 MPa differential pressure
3.3 进、出口压差的影响
当进、出口压差分别为1.5、3、5 MPa时,阀芯以0.1 m/s速度匀速开启和关闭情况下进行仿真计算,得到阀芯所受的液动力对比图,如图8所示.

图8 不同进、出口压差下的液动力曲线Fig.8 Flow force curves under different differentialpressure
由图8可见,压差越大,作用在阀芯上的液动力越大,这是由于进出控制体的液流动量变化率与压差成正比的缘故,同时液动力滞环随压差的增大越明显.
3.4 节流槽个数的影响
在进、出口压差为1.5 MPa,阀芯以0.1 m/s速度匀速开启和关闭的情况下,在阀芯凸肩圆周方向均布2个和4个U形槽的情况下进行仿真计算,得到阀芯所受的液动力对比,如图9所示.可见,U形槽个数越多,作用在阀芯上的液动力反向增大,这是由于节流槽个数越多,通流面积越大,进出控制体的液流动量变化率越大的缘故;液动力滞环随节流槽个数的增多越明显,且在阀口小开度下出现了液动力方向变化的现象.

图9 不同节流槽个数下的液动力曲线Fig.9 Flow force curves under different number of notch
4 结 论
(1) 当阀芯运动速度低于0.1 m/s时,阀芯运动时所受的液动力与阀口开度一定稳态计算时液动力相差不大,可以用瞬态计算近似稳态计算,得到连续的液动力变化曲线并可避免稳态计算时网格重复划分的繁琐过程.
(2) 当阀芯运动方向改变时,液动力出现滞环现象,速度越大,滞环越大并在高速开关运动小开口位置时出现液动力方向变化问题;进、出口压差越大,节流槽个数越多,阀芯所受的液动力增大,滞环越明显;阀芯运动速度越高,阀芯所受的液动力与稳态计算时液动力的偏离越大,在高动态性能液压阀设计时必须考虑阀芯瞬态运动对液动力的影响.
[1] 冀宏,傅新,杨华勇.非全周开口滑阀稳态液动力研究[J].机械工程学报,2003, 39(6): 13-17.
JI Hong, FU Xin, YANG Hua-yong. Study on steady flow force of non-circular opening spool valve [J]. Chinese Journal of Mechanical Engineering, 2003, 39(6):13-17.
[2] AMIRANTE R, DEL VESCOVO G, LIPPOLIS A. Flow forces analysis of an open center hydraulic directional control valve sliding spool [J]. Energy Conversion and Management, 2006, 47(1): 114-131.
[3] AMIRANTE R, MOSCATELLI P G, CATALANO L A. Evaluation of the flow forces on a direct (single stage) proportional valve by means of a computational fluid dynamic analysis [J]. Energy Conversion and Management, 2007, 48(3): 942-953.
[4]方文敏,成琳琳,傅新,等.带U形节流槽的滑阀稳态液动力研究[J].浙江大学学报:工学版,2010, 44(3):574-580.
FANG Wen-min, CHENG Lin-lin, FU Xin, et al. Investigation on steady state flow force of spool valve with U-grooves [J]. Journal of Zhejiang University: Engineering Science, 2010, 44(3): 574-580.
[5] 吴晓明,要继业,李伟,等.U+K节流槽滑阀的数值模拟[J].流体传动与控制,2010, 5: 13-16.
WU Xiao-ming, YAO Ji-ye, LI Wei, et al. The numerical simualtion of spool valve with U+K notches [J]. Fluid Power Transmission and Control, 2010, 5: 13-16.
[6] 高俊庭,殷晨波,叶仪,等.非全周开口的液压滑阀内部流场的CFD解析[J].液压与气动,2013, 5: 58-61.
GAO Jun-ting, YIN Chen-bo, YE Yi, et al. CFD simulation of flow field in hydraulic spool valve with notches [J]. Chinese Hydraulic and Pneumatics, 2013, 5: 58-61.[7] 叶仪,殷晨波,刘辉,等.节流槽阀口静态流动特性研究[J].农业机械学报,2014, 45(6): 308-316.
YE Yi, YIN Chen-bo, LIU Hui, et al. Stationary flow characteristics of notches on throttling grooves [J]. Transaction of the Chinese Society for Agricultural Machinery, 2014, 45(6):308-316.
[8] DEL VESCOVO G, LIPPOLIS A. Review analysis of unsteady forces in hydraulic valves [J]. International Journal of Fluid Power, 2006, 7(3): 29-39.
[9] 赵蕾,陈青,权龙.阀芯运动状态滑阀内部流场的可视化分析[J].农业机械学报,2008,39(11): 142-146.
ZHAO Lei, CHEN Qing, QUAN Long. Visualizaion of the flow field in a moving spool valve [J].Transaction of the Chinese Society for Agricultural Machinery, 2008,39(11): 142-146.
[10] POSA A, ORESTA P, LIPPOLIS A. Influence of the spool velocity on the performance of a directionalhydraulic valve [J]. International Journal of Fluid Power, 2013, 14(3): 15-25.
[11] 王东升.节流槽滑阀阀口流量系数及稳态液动力计算的研究[D].兰州:兰州理工大学,2008: 42-43.
WANG Dong-sheng. Investigation into flow coefficient of orifice and caculation of steady flow force of spool valve with notches [D]. Lanzhou: Lanzhou University of Technology, 2008: 42-43.
[12] 冀宏,侯敏,王金林,等. 液动多路阀主阀芯瞬态运动的实测[J].机床与液压,2011, 39(23): 6-9.
JI Hong, HOU Min, WANG Jin-lin, et al. Measurement of dynamic motion of spool in hydraulic operated mutiway valve [J]. Machine Tool and Hydraulics, 2011, 39(23): 6-9.
Transient simulation on flow force of non-circular opening spool valve
WANG Jian-sen, LIU Yao-lin, JI Hong, WANG Peng-fei
(KeyLaboratoryofFluidMachineryandSystems,LanzhouUniversityofTechnology,Lanzhou730050,China)
The oil outflow condition in the spool valve with U shaped notches was analyzed as an example in order to obtain the flow forces characteristics of the non-circular opening spool valve in spool movement process under such conditions as different spool speed, direction of movement, pressure differential and throttle slot numbers. The non-conformal, sliding mesh techniques and UDF programming method were adopted. Numerical results show that there is only marginal difference between the flow forces obtained from steady and transient calculations when the spool speed is below 0.1 m/s, so transient calculation can be approximately used in place of steady state calculation. The deviation between these two simulation results became more obvious with the increase of spool speed. The flow force hysteresis appeared when the spool motion direction changed. Flow force redirection happened when the spool approaching to small valve opening with big speed in closing movement. The hysteresis became more obvious with the addition of spool speed, pressure differential and throttling groove number.
spool valve; non-circular opening; flow force; valve movement
2015-09-17.
国家自然科学基金资助项目(51575254).
王建森(1973—),男,副教授,从事液压元件基础理论的研究.ORCID: 0000-0002-6435-9413.E-mail: wajase@163.com
冀宏,男,教授. ORCID: 0000-0002-3578-2810. E-mail: jihong@lut.cn
10.3785/j.issn.1008-973X.2016.10.011
TH 137
A
1008-973X(2016)10-1922-05
浙江大学学报(工学版)网址: www.zjujournals.com/eng

