PMMA表面与深度吸收热解过程数值模拟

龚俊辉, 陈怡璇, 李 劲, 周 洋

(1.南京工业大学 安全科学与工程学院,江苏 南京 211816；2.纽黑文大学 火灾科学系,美国 康涅狄格州 西黑文市 06516；3.中南大学 消防工程系,湖南 长沙 410075)



PMMA表面与深度吸收热解过程数值模拟

龚俊辉1, 陈怡璇1, 李 劲2, 周 洋3

(1.南京工业大学 安全科学与工程学院,江苏 南京 211816；2.纽黑文大学 火灾科学系,美国 康涅狄格州 西黑文市 06516；3.中南大学 消防工程系,湖南 长沙 410075)

通过建立一维热解模型,对聚甲基丙烯酸甲酯(PMMA)在外界辐射热流密度条件下的热解过程进行数值模型的构建,研究表面吸收和深度吸收这两种文献中用的较多且相对极端的吸收方式对材料热解过程的影响.该数学模型对锥型量热仪氮气气氛下材料热解实验过程进行模拟,包括质量损失速率、材料内部温度分布、表面和背面温度.通过与已经发表的相应实验数据对比,对模型的可靠性进行验证.结果表明,不同的吸收模式对热解细节有较大的影响,如材料内部温度分布、表面温度和热解开始时间等.在预测实验尺寸条件下的热解过程时,两种吸收模式的模拟结果均在可接受范围之内.

PMMA；热解；深度吸收；表面吸收

火灾中聚合物材料物理现象的模拟对预测火灾发展过程有重要意义.理论分析模型和数值计算模型都涉及气相流体力学、化学动力学、固相热解、浓缩相和气相交界面上的传热传质过程等.气相问题已经被研究多年且相对成熟[1-2],而固相热解过程没有被充分研究.

在大规模火灾中,辐射传热是未燃材料接收到的火灾热反馈的主要传热形式[3-4].材料对辐射热流的吸收决定了着火延滞时间tig、临界热流HFcri、临界质量流率(MLRcri)和之后的燃烧速率[5-7].外部辐射热流到达聚合物材料(红外半透明介质)表面后在表面发生反射、表面吸收(surface absorption)和透射过材料表面3种现象[8],透射过表面进入材料内部的热流在传输过程中逐渐被吸收,即深度吸收(in-depth absorption).研究表明,对于大部分聚合物,表面反射率不超过3%[3],即绝大部分能量通过表面和深度吸收的方式被用于预加热和热解材料.

在早期的热解研究中,学者们认为对热厚的聚合物材料,当表面被加热到一个临界温度(即热解温度Tp)后,材料以无限快的速率瞬间由固态转化为气态,即表面吸收[9-14].之后,DI Blasi等[15-20]对该类模型进行改进并考虑有限速率的热解反应,即用一步单阶阿伦尼乌斯方程来精确模拟热解过程.Stoliarov等[21-26]通过热重分析法(TGA)和示差扫描量热法(DSC)结合ThermaKin[22]对碳化和非碳化聚合物材料的热力学和动力学参数与温度的关系进行测试.

在很多研究中,即使对红外半透明介质,为了模型简化也采用表面吸收假设.Hallman等[23-25]发现,聚合物材料的着火时间受表面吸收的影响很大,Saito等[26]发现,深度吸收是造成PMMA着火延迟的主要原因,特别是在高热流密度情况下.Jiang等[6-7]用水冷的方法对几种聚合物材料的深度吸收系数进行测量.

本文建立新的综合考虑表面和深度吸收过程的数值模型,对PMMA在外部辐射热流加热情况下的热解过程进行研究,对之前文献中采用的两种极端的热流吸收模式进行讨论.该模型除在分别研究单一吸收模式合理性方面以外,对两种吸收模式同时存在情况下的组合吸收热解过程有较好的适用性,而该领域目前还处在探索阶段.

1 模型介绍

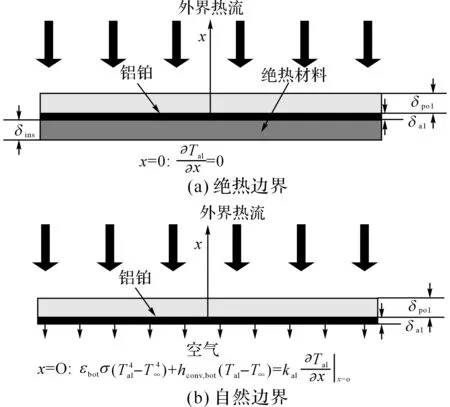
图1 PMMA热解物理模型图Fig.1 Physical model of PMMA degradation

为了模拟对应氮气气氛下锥型量热仪上的PMMA热解过程[25],与之对应的物理模型如图1所示,坐标原点设置在铝箔的下表面处.热流密度为20、40和60 kW/m2.样件上表面与空气接触,下表面与铝箔接触,为了分别模拟PMMA背面热电偶测温实验和红外热相仪测温实验,背面采用2种边界条件,即背面绝热边界和背面自然边界,如图1(a)、(b)所示.

1.1 控制方程

半透明聚合物表面对照射到其上的外部热流的反射、吸收和透射过程[8]可以表达为

r+τ+ω=1.

(1)

式中：r、τ和ω分别为表面的反射率、吸收率和透射率,分别表征表面反射、吸收和透射热流与入射热流的比值.这些表面参数均与入射热流辐射波长和入射角有关,本文采用全波长平均数且忽略入射角的影响[22，24-25,27].材料内部透射进来的热流强度与材料的深度吸收系数有关且呈指数衰减：

(2)

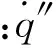
一维固相能量方程包括PMMA内部能量方程和铝箔内能量方程.为了研究表面和深度吸收两种吸收模式,τ和κ同时被引入能量方程：

(3)

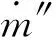
(4)

PMMA和铝箔内部连续性方程可以分别表达为

∂ρs/∂t=ρsSv,

(5)

∂ρal/∂t=0.

(6)

PMMA内部热解速度或挥发分生成速率可以表达为

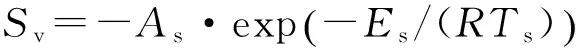
(7)

式中：As为指前因子,Es为活化能,R为理想气体常数.总的质量损失速率可以表达为

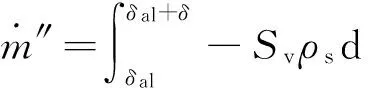
(8)

1.2 初始条件和边界条件

初始条件为

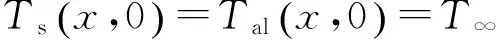
(9)

(10)

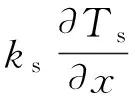
(11)

式中：εpol、σ、hconv,top分别为表面发射率、斯蒂芬玻尔兹曼常数和上表面对流换热系,且假定上表面吸收率和发射率相等(基尔霍夫定律)[30],即εpol=τ.材料和铝箔交界面上的传热过程可以表达为x=δal：

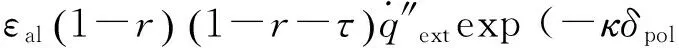
(12)

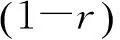
铝箔下表面处有2种边界条件,如图1所示.第一种绝热边界为

(13)

第二种自然边界,包括向环境的对流和辐射：

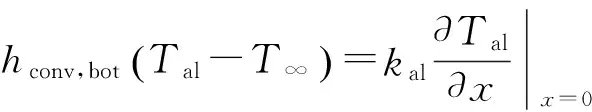
(14)

式中：εbot,al和hconv,bot分别为铝箔下表面发射率和自然对流换热系数. 方程(11)、(14)中的hconv,top和hconv,bot可以通过热平板上表面和下表面的经验公式[8]计算得到：

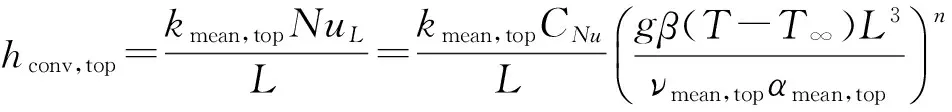
(15)

(16)

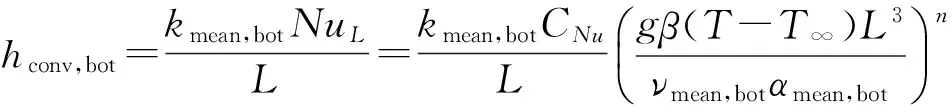
(17)

CNu=0.27,n=1/4.

(18)

式中：L为特征长度,对于方形样件,

L=A/P.

(19)

式中：A为面积，P为周长.式(15)、(17)中的kmean,top和kmean,bot可以通过膜温计算：

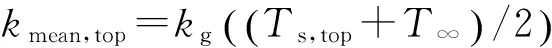
(20)

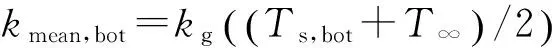
(21)

式中[28]：

1.018 4×10-4T-3.933 3×10-4.

(22)

热扩散率可以表达为

αmean,top=kmean,top/(ρgcp,g),

(23)

αmean,bot=kmean,bot/(ρgcp,g).

(24)

式中：cp,g为气体比定压热容,是常数,

cp,g=const=1.063 J/(g·K) ;

(25)

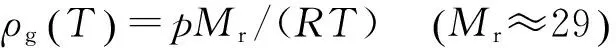
(26)

式中：p为气体压力，Mr为相对分子质量.式(15)、(17)中的气体膨胀系数β和动力黏度νg[29]为

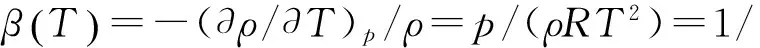
(27)

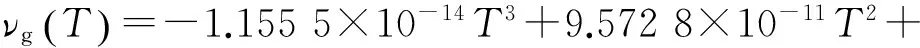
3.760 4×10-8T-3.448 4×10-6(m2·s-1).

(28)

当上表面温度从300 K上升到700 K时,hconv,top从0增大到13.26 W/(m2·K).同样,hconv,bot从0增大到4.3 W/(m2·K).

1.3 计算方法

模拟中,PMMA样件厚度均为6 mm,铝箔厚度为0.3 mm.非线性偏微分方程通过控制容积法进行离散得到离散方程,PMMA和铝箔内均采用相同尺寸的均匀网格.在热解过程中,假定材料变薄的过程只发生在材料表面,即最表层,当最表面网格内材料密度小于原始密度的5%(ρpol,top≤0.05ρpol,∞)时,认为该层材料热解完成,次表层网格变为最表层网格.由于控制方程中有能量源项且材料热物性参数为温度的函数,计算方法采用半隐式格式.能量源项和物性温度函数均为非线性项,半隐式格式可以根据最新迭代结果计算出最新源项和物性参数并根据收敛条件进行修正,在保证计算精度的前提下大大加快收敛速度.在每一时间步长内都进行重复迭代,直至达到相应的收敛条件,即两次计算所得所有区域内网格差别的最大值小于设定要求0.001 K：

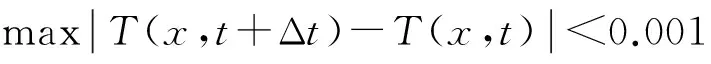
(29)

模拟中所用到的PMMA和铝箔热物理参数和化学动力学参数如表1所示.计算总时间、时间步长、初始和环境温度、材料表面反射率分别为3 000 s、1 s、300 K和0.05.每一时间步内的质量损失速率可以通过式(8)计算得到.

表1 PMMA和铝箔计算参数

Tab.1 Parameters of polymers and aluminum used in simulation

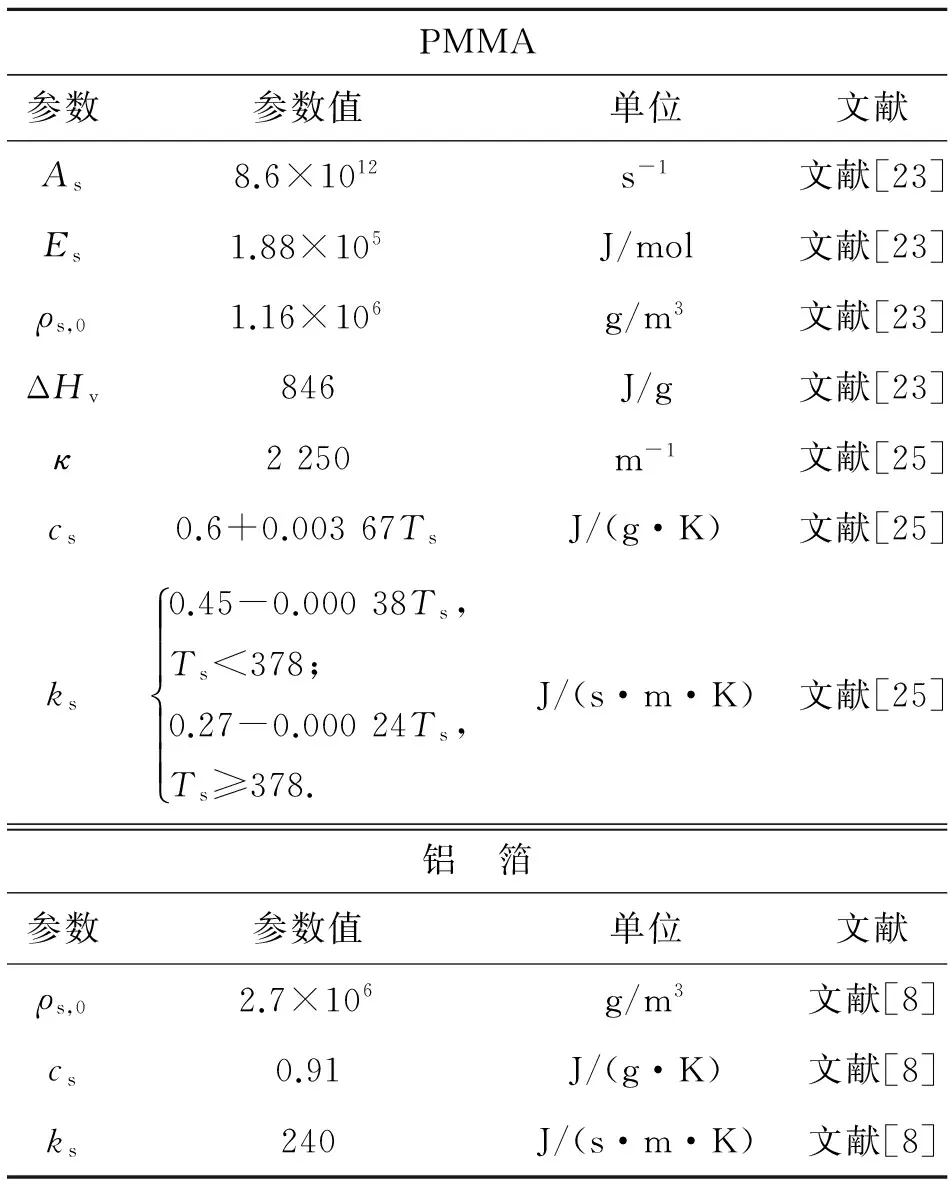
PMMA参数参数值单位文献As8.6×1012s-1文献[23]Es1.88×105J/mol文献[23]ρs,01.16×106g/m3文献[23]ΔHv846J/g文献[23]κ2250m-1文献[25]cs0.6+0.00367TsJ/(g·K)文献[25]ks0.45-0.00038Ts,Ts<378;0.27-0.00024Ts,Ts≥378.ìîíïïïïJ/(s·m·K)文献[25]铝 箔参数参数值单位文献ρs,02.7×106g/m3文献[8]cs0.91J/(g·K)文献[8]ks240J/(s·m·K)文献[8]

2 结果与讨论

2.1 表面吸收与深度吸收

大部分研究聚合物材料燃烧特性的模型都采用两种经典假设：表面吸收和深度吸收.表面吸收(ω=0)认为热流只在材料表面被吸收,外部热流被当作边界条件处理；深度吸收(τ=0)认为热流在透射过材料时被逐渐吸收,外部热流被当作控制方程中的能量源项.这两种假设对半透明介质都比较理想和极端.

如图2所示为分别采用2种吸收模式不同热流和背面绝热条件下PMMA最上面10个网格在热解过程中的温度模拟结果随时间的变化曲线,其中网格大小为0.1 mm.表面吸收情况下,10条曲线间明显存在差异,即材料表面下的这部分区域内存在较大的温度梯度.传导热热流可以通过模拟结果估算出来：q″cond=ksΔTs/Δx.在20、40、60 kW/m2热流密度下,最上面两层网格间的温度差为4、16、28 K,表面温度大约为645、675、700 K,材料导热率通过表1可以计算为：0.115 2、0.108 0、0.102 0 W/(m·K).相应的导热热流密度为4.6、17.28、28.56 kW/m2.材料表面吸收的净热流密度大小可以通过式(11)的左半部分计算为5.6、22.3、39.2 kW/m2,其中hconv,top通过式(15)计算.这意味着在第一层网格内被用于加热和热解PMMA材料的热量分别为1.0、5.02、10.64 kW/m2.很显然,照射到材料表面被吸收用于加热和热解的热量占总入射热流密度的比例分别为28%、55.75%、65.33%,其他均以对流和辐射的形式通过表面散失到环境中.与表面吸收不同,深度吸收情况下,最上面10层网格内温度梯度较小,特别是最上面几层(热穿透层)基本上没有温度差,这意味着这些体积内的材料主要通过深度吸收的方式被加热而不是热传导,热穿透层下的传热过程主要受热传导控制.类似的现象在PMMA自然对流背面边界条件下同样存在,如图3所示.

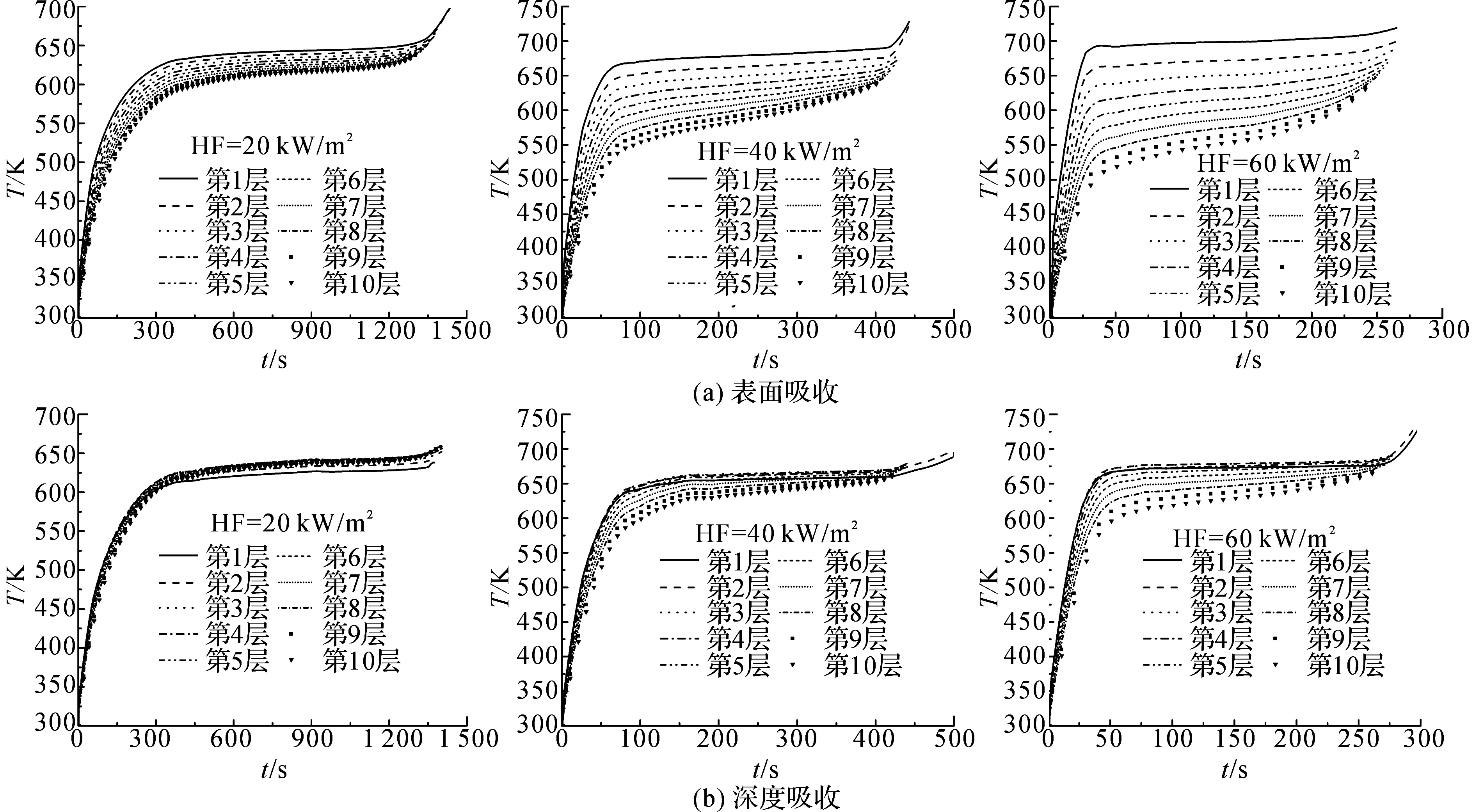
图2 两种吸收模式不同热流和背面绝热条件下PMMA最上面10层网格热解过程中的温度模拟结果曲线Fig.2 Simulated temperatures of first top 10 meshes of PMMA with in-depth and surface absorption in thermal-adiabatic bottom boundary condition under different heat flux

导致深度吸收情况下热穿透层内较均匀温度分布的另一个主要原因是材料表面向环境的热损失.在最表层网格内,一方面材料被透射过热流加热,另一方面通过辐射和对流向环境中散热,但在第二层及以下风格中,没有向环境中的热损失.受表面热损的影响,最表层的温度甚至低于其下的几层网格温度.如图4所示为PMMA两种背面边界条件下表面吸收和深度吸收模拟的材料内部温度分布.在表面吸收模式下,材料内部温度从底部到表面持续增大,但在深度吸收情况下,内部温度从底部开始上升,快到表面时达到最大值,然后下降直到表面.如文献[7]所述,1/κ可以用于估算热流穿过材料的热穿透层厚度；对于透明的PMMA,当κ=1 870 m-1时大约80%的热量在最表面的0.534 mm厚度范围内被材料吸收,即在该厚度内深度吸收占主导,其他区域热传导占主导.本文中PMMA,κ=2 250 m-1,相应的热穿透层厚度约为0.44 mm,即最表面的4层网格.表面的热损失和净热量吸收率可以采用上表面对流换热和辐射散热的方法计算.

在文献[9～14]的表面吸收模型中,为了计算方便,表面温度Tp作为热解开始温度或空气环境中材料着火的判据被视为材料的特有参数且不随外部热流密度的变化而变化,即采用无限快热解反应速率.如图5所示为PMMA不同热流密度下的表面温度模拟结果.在两种吸收模式下,表面温度均随热流密度的增大而增大,且背面边界条件对表面温度的影响较小.Lautenberger等[30]在研究热流密度为0～200 kW/m2条件下PMMA的着火过程时发现,表面温度随热流密度增大而增大,将临界质量流率作为着火的临界判据.Lautenberger给出的解释是在高热流密度条件下,热解发生在表面的一薄层内,为了达到临界的质量流率,该内层的热解速率相对较高,对应的热解时的温度较高,即表面温度.本文中,较大的外部热流密度导致材料热穿透层内较高的反应速率,即较高的表面温度,如式(7)所示.

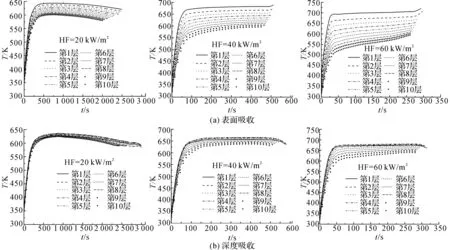
图3 两种吸收模式不同热流和背面自然条件下PMMA最上面10层网格热解过程中温度模拟结果曲线Fig.3 Simulated temperature of first top 10 meshes of PMMA with in-depth and surface absorption in free convection bottom boundary condition under different heat flux

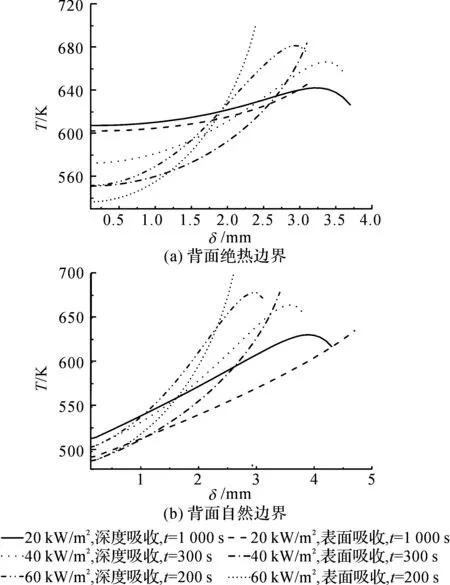
图4 PMMA表面和深度吸收材料内部温度分布模拟结果Fig.4 Temperature distribution in condensed phase of PMMA with both hypotheses during gasification

在不同热流密度条件下,表面吸收情况下的表面温度较深度吸收情况下的高,如图5所示.材料所吸收的热量集中在热穿透层内,表面吸收情况下该层内存在较大的温度梯度,导致表面温度相对较高；在深度吸收情况下,热穿透层内的温度分布较均匀,表面温度较低.

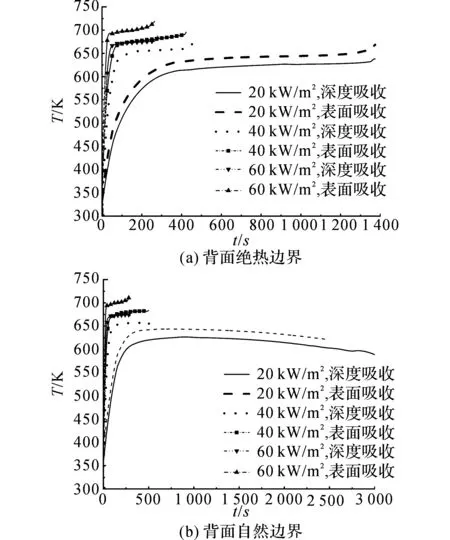
图5 PMMA不同热流下表面温度模拟结果Fig.5 Top surface temperature of PMMA of modelunder varying HF

事实上，非碳化聚合物对于外部热流来说，为半透明介质,在热解过程中2种吸收模式现时存在.Jiang[6]发现,即使在PMMA表面涂了黑色碳层的条件下深度吸收依然存在,并指出需要进行更进一步的研究以分析表面和深度吸收过程的综合作用.本文对表面吸收占总吸收热流的不同百分比进行研究,即τ从0(0%)变化到1-r(100%).如图6所示,不同百分比下背面温度的模拟结果非常相近,这说明不同吸收模式对背面温度没有太大影响.如图7所示为不同百分比下的质量损失速率曲线,模拟结果比较相近.表面吸收导致的较高表面温度会使热解开始时间较早,深度吸收情况下较低的表面温度会延迟热解开始时间,特别是在高热流情况下更明显.类似地,如果是在空气气氛下,深度吸收会导致材料着火时间的延迟,即验证了Jiang[6]的结论.尽管如此,在整个热解时间期内,两种吸收模式模拟结果的差别不是特别大,在模拟实验尺寸条件下均在可接受范围之内.

2.2 质量损失速率(mass loss rate, MLR)

对2种吸收模式下的模型模拟结果和已经出版的实验数据进行对比说明.对比参数为PMMA背面绝热和自然边界条件下的质量损失速率.

如图8所示为PMMA模拟结果与实验数据对比图.在相同热流密度条件下,图8(b)的持续时间较图8(a)长,质量损失速率较低,主要是因为在背面自然边界条件下(见图8(b)),部分热量会散失到环境中.模型的模拟结果较好,但在图8(a)中,MLR的最大值在表面吸收情况下较深度吸收大,且高出实验数据较大.这主要是因为在热解的最后阶段,当材料厚度减小到与热穿透层厚度相当或更小时,受表面吸收过程的影响,整个材料温度较深度吸收情况下高,如图9所示.在60和40 kW/m2热流密度下该现象比较明显,20 kW/m2时由于热流和净吸收率都较小,该现象不是很明显.

2.3 背面温度

该部分将背面温度的模拟结果和实验数据进行对比来验证模型.如图10所示为PMMA背面绝热边界热流密度为20和60 kW/m2条件下用热电偶所测背面温度[31]和模拟结果对比.可以看出,2种吸收模式下的模拟结果均较好.

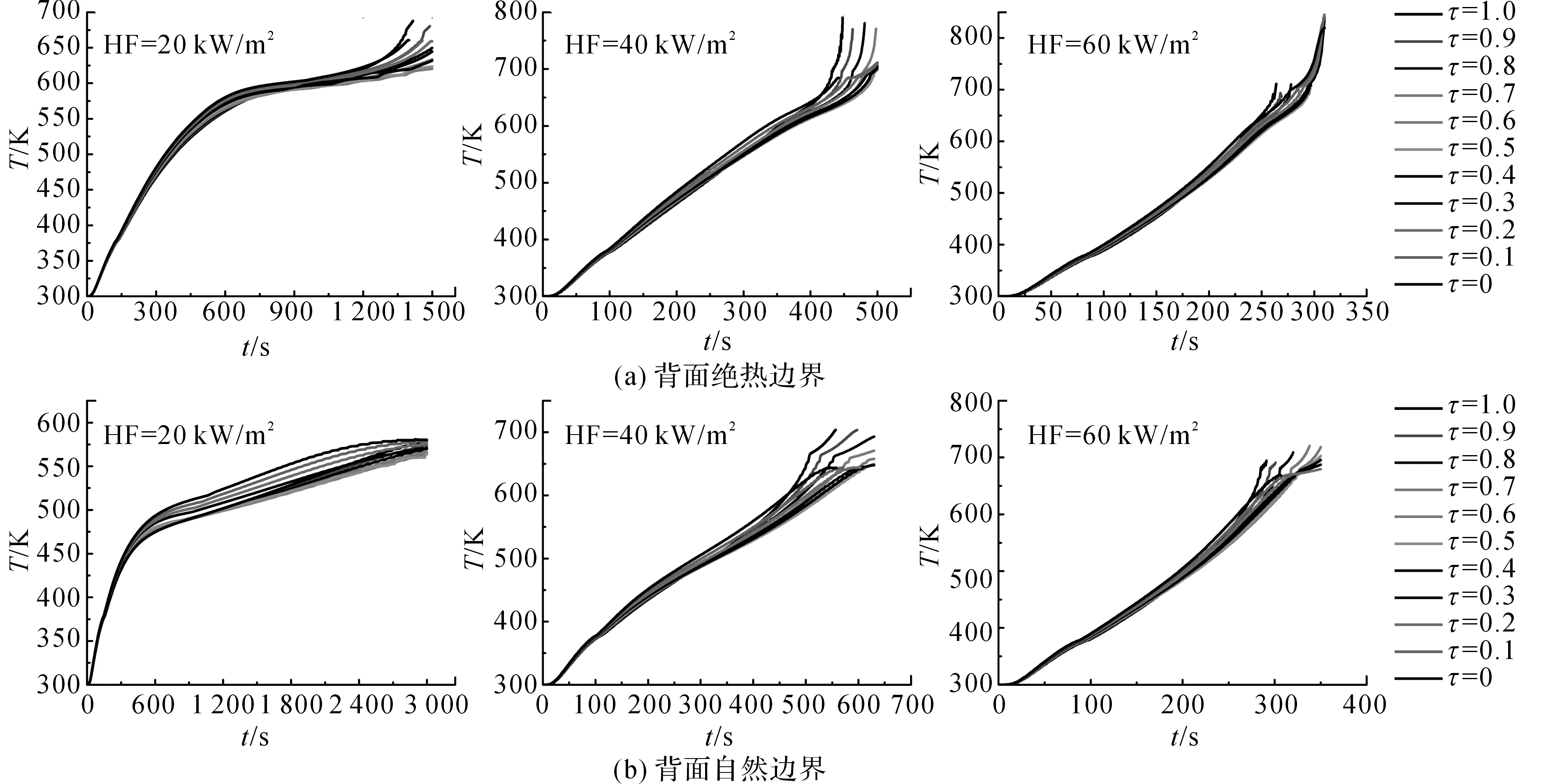
图6 PMMA表面吸收百分比对背面温度的影响Fig.6 Effect of percentage of surface absorption on bottom surface temperature of PMMA convection bottom boundary condition

图7 PMMA表面吸收百分比对质量损失速率的影响Fig.7 Effect of percentage of surface absorption on mass loss rate of PMMA

图8 PMMA质量损失速率模拟结果和实验结果对比Fig.8 Comparison of mass loss rate of PMMA between model results and experimental results

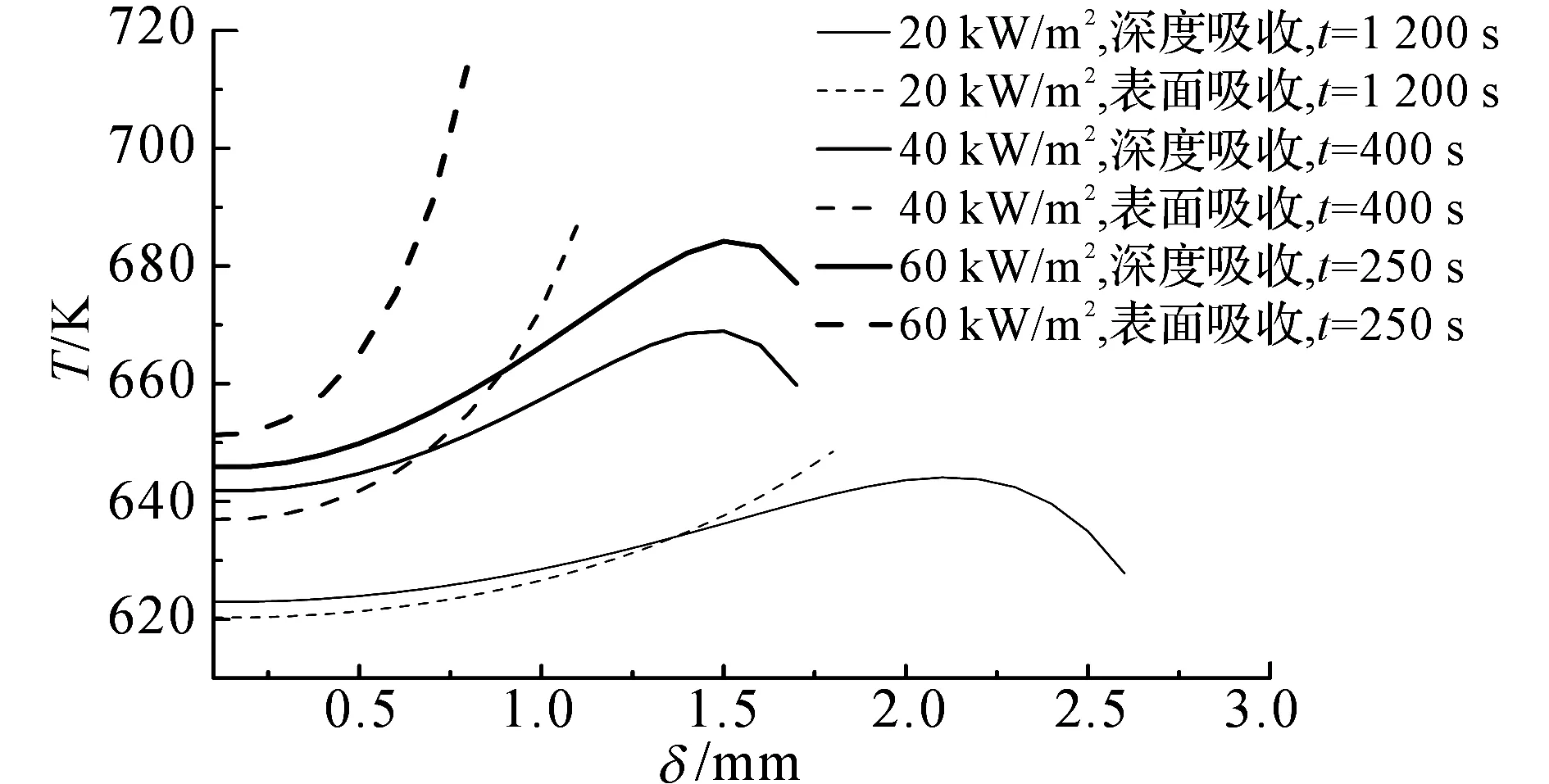
图9 PMMA背面绝热条件下MLR最大值时材料内部温度分布Fig.9 Temperature distribution of PMMA with thermal-adiabatic bottom at time corresponding to maximum value of MLR

如图11所示为用红外热像仪所测PMMA不同热流密度和背面自然边界条件下样件背面温度的模拟和实验结果对比.在不同热流密度下,2种吸收模式模拟结果在模拟实验尺寸热解过程中均可接受,小热流密度情况下表面吸收模拟结果偏差最大.这是因为表面吸收时较高的表面温度过高地估算了由上表面损失到环境中的热量,而该部分热量占总入射热流密度的比例较大所造成的,在大热流密度下,该比例下降,表面热损失整个热解模拟过程造成的影响越来越小.

与2.1节的分析过程类似,通过式(11)和(14)可以计算出PMMA深度吸收情况下上、下表面通过辐射和对流损失到环境中的热量.当下表面温度达到550 K时,hconv,bot和下表面热损失为4.0 W/(m2·K)和5.73 kW/m2.在热流密度为20、40、60 kW/m2的条件下，相应时刻分别为1 735、384、231 s,相应的上表面温度分别为613.4、656.8、674.4 K,上表面热损失分别为11.25、14、27、15.64 kW/m2.这意味着此时吸收热量的84.9%、50.0%、35.62%散失到环境中.材料对热流密度的净吸收率从最开始的1-r逐渐减小到一个较低的值.在20 kW/m2热流密度下,较低的外界热流密度和低的净吸收率导致了较长的热解时间.

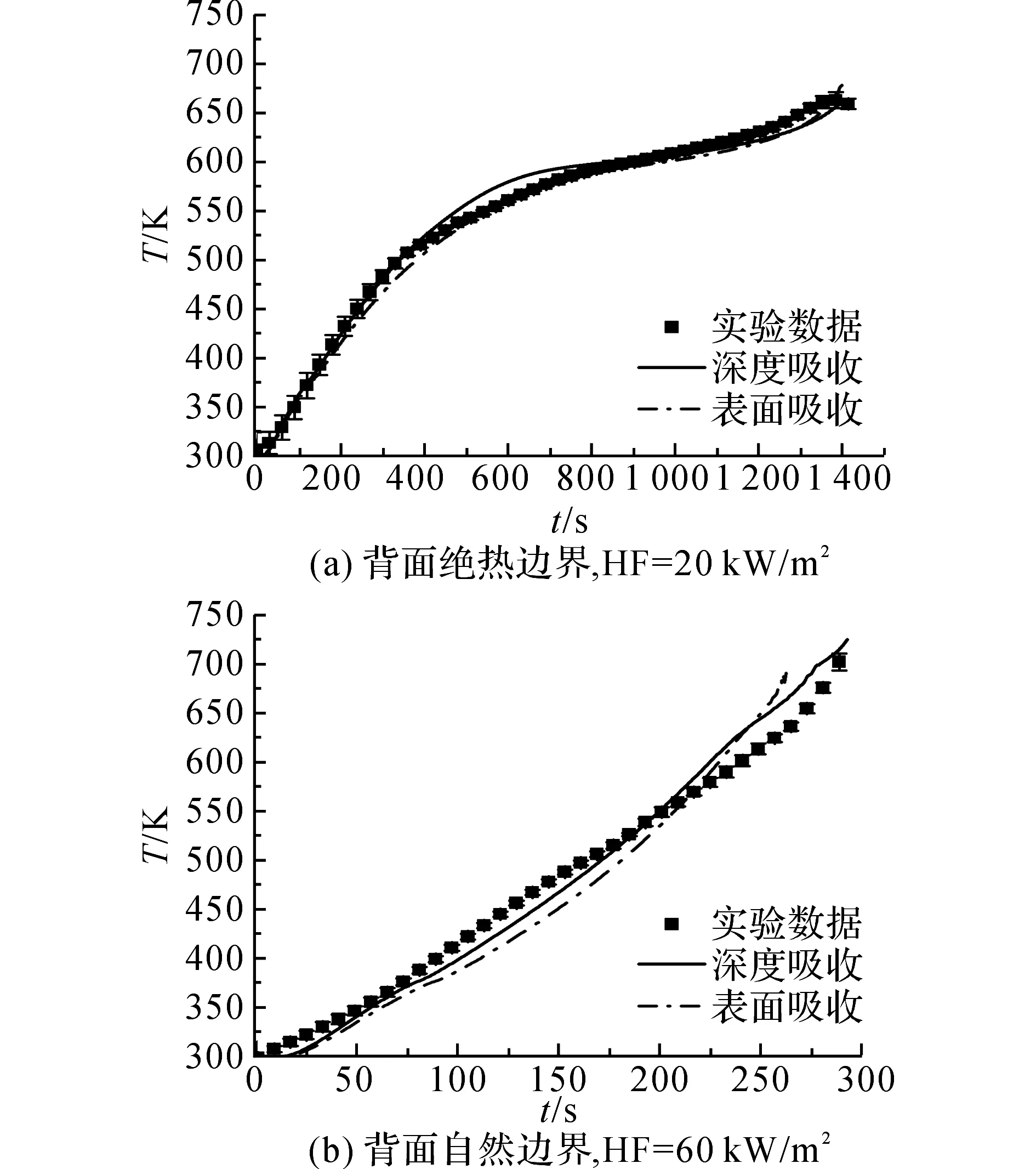
图10 PMMA背面绝热条件下热电偶所测背面温度和模拟结果对比Fig.10 Comparison of bottom surface temperature of PMMA between model and experiments, employing thermocouples method, with insulated boundary condition

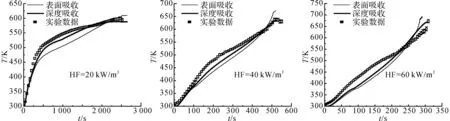
图11 PMMA背面自然边界条件下背面温度模拟和实验结果对比Fig.11 Comparison of bottom surface temperature of PMMA between model and experiments, employing IR camera method, with free convection boundary condition

3 结 论

(1) 在表面吸收情况下,热穿透层内温度梯度较大,传热过程主要受固相热传导控制；在深度吸收情况下,热穿透层内温度分布较均匀,传热过程主要靠深度吸收来实现,热穿透层下,传热过程主要为固相热传导.

(2) 在相同的热流密度下,表面吸收情况下的表面温度较深度吸收高；表面温度随外部热流密度的增大而增大；2种吸收模式对背面温度的影响不大.

(3) 在低热流密度下,较低的热流密度净吸收率是导致热解速率较慢和时间较长的另一个重要原因.

(4) 2种吸收模式模拟结果与实验数据的对比误差都在可接受范围内,即当不涉及热解细节时,两种假设在模拟实验尺寸条件的热解过程时均可采用,但精确度须进行进一步的研究来提高.

(5) 本文关于PMMA热解过程的研究突破传统单一热流密度吸收模式的限制,综合考虑两者的影响,为之后研究不同合理组合方式及热解模型的改进有重要意义,为其他聚合物材料热解过程研究提供了参考方法.此外,本文所涉及到的关于材料热解着火的一些方法、数据和结论,可为该类材料相关安全标准、检测规范和消防法规等文件的制定提供参考.

[1] RICHARD N W, NATALLIA S, RICHARD E L. A microscale combustion calorimeter study of gas phase combustion of polymers [J]. Combustion and Flame, 2015, 162(3): 855-863.

[2] DAI Jia-kun, MICHAEL A D, YANG Li-zhong, et al. Piloted ignition and extinction for solid fuels [J]. Proceeding of the Combustion Institute, 2013, 34(2): 2487-2495.

[3] EGOLFOPOULOS F N, HANSEN N, JU Y, et al. Advances and challenges in laminar flame experiments and implications for combustion chemistry [J]. Progress in Energy and Combustion Science, 2014, 43(6): 36-67.

[4] MASTORAKOS E. Ignition of turbulent non-premixed flames [J]. Progress in Energy and Combustion Science, 2009, 35(1): 57-97.

[5] FERERES S, FERNANDEZ-PELLO C, URBAN D L, et al. Identifying the roles of reduced gravity and pressure on the piloted ignition of solid combustibles [J]. Combustion and Flame, 2015, 162(4): 1136-1143.

[6] JIANG Feng-hui, DE RIS J L, KHAN M M. Absorption of thermal energy in PMMA by in-depth radiation [J]. Fire Safety Journal, 2009, 44(1): 106-112.

[7] LINTERIS G, ZAMMARANO M, WILTHAN B, et al. Absorption and reflection of infrared radiation by polymers in fire-like environments [J]. Fire and Materials, 2012, 36(7)： 537-553.

[8] INCROPERA F P, DEWITT D P, BERGMAN T L, et al. Fundamentals of heat and mass transfer [M]. 6th ed．New York: Wiley, 2007: 752.

[9] WHITING P, DOWDEN J M, KAPADIA P D, et al. A one-dimensional mathematical model of laser induced thermal ablation of biological tissue [J]. Lasers in Medical Science, 1992, 7 (7): 357-368.

[10] BILLINGS M J, WARREN L, WILKINS R. Thermalerosion of electrical insulating materials [J]. IEEE Transaction on Electron Insulation, 1971, 6(2): 82-90.

[11] DELICHATSIOS M A, CHEN Y. Asymptotic, approximate and numerical solutions for the heatup and pyrolysis of materials including reradiation losses [J]. Combustion and Flame, 1983, 92(3): 292-307.

[12] QUINTIERE J, IQBAL N. An approximate integral model for the burning rate of a thermoplastic-like material [J]. Fire and Materials, 1994, 18(2): 89-948.

[13] STAGGS J E J. A discussion of modeling idealized ablative materials with particular reference to fire testing [J]. Fire Safety Journal, 1997, 28(1): 47-66.

[14] TEWARSON A, PION R F. Flammability of plastics-I. burning intensity [J]. Combustion and Flame, 1976, 26(6): 85-103.

[15] DI BLASI C, WICHMAN I S. Effects of solid-phase properties on flames spreading over composite materials [J]. Combustion and Flame, 1995, 102(3): 229-240.

[16] 金杨.不同热流条件下聚合物的热解动力学研究[D].青岛：青岛科技大学，2004.

JIN Yang. Thermal decomposition and kinetics of polymers exposed to varied heat fluxes [D]. Qingdao: Qingdao University of Science and Technology, 2004.

[17] STAGGS J E J, WHITELEY R H. Modeling thermal degradation of polymers using single-step first-order kinetics [J]. Fire Safety Journal, 1999, 32(1): 17-34.

[18] 徐亮，伍卫军，丁严艳.典型热塑性聚合物热解行为研究[J].火灾科学,2010,19(3): 143-149.

XU Liang, WU Wei-jun, DING Yan-yan. Investigation on thermal degradation behavior of typical thermoplastics polymer [J]. Fire Safety Science, 2010,19(3): 143-149.

[19] STAGGS J E J. A theoretical investigation into modeling thermal degradation of solids incorporating finite rate kinetics [J]. Combust Science and Technology, 1997, 123(1): 261-285.

[20] WICHMAN I S, ATREYA A. A simplified model for the pyrolysis of charring materials [J]. Combustion and Flame, 1987, 68(3): 231-247.

[21] STOLIAROV S I, WALTERS R N. Determination of the heats of gasification of polymers using differential scanning calorimetry [J]. Polymer Degradation and Stability, 2008, 93(2): 422-427.

[22] STOLIAROV S I, LYON R E. Thermo-Kinetic model of burning [EB/OL]. 2008-08-17. http:∥www.fire.tc.faa.gov/reports/reports.asp.

[23] HALLMAN J R, WELKER J R, SLIEPCEVICH C M. Ignition of polymers Ignition time depends on incident irradiance, the nature of the radiation source, and the optical properties of the material [J]. SPE Journal, 1972, 28(3): 43-47.

[24] HALLMAN J R, SLIEPCEVICH C M, WELKER J R. Radiation absorption for polymers: the radiant panel and carbon arcs as radiant heat source [J]. Plos One, 2013, 8(3): 462-469.

[25] LINAN A, WILLIAMS F A. Radiant ignition of areactive solid with in-depth absorption [J]. Combustion and Flame, 1972, 18(1)： 85-97.

[26] DELICHATSIOS M A, SAITO K. Upward fire spread: key flammability properties, Similarity solution and flammability indices [R]. Rhode Island: FM Global, 1991.

[27] TSILINGIRIS P T. Comparative evaluation of theinfrared transmission of polymer films [J]. Energy Conversion and Management, 2003, 44(18): 2839-2856.

[28] Thermal conductivity of air vs. temperature [EB/OL]. 2010-01-24. http:∥bouteloup.pierre.free.fr/lica/phythe/don/air/air_k_plot.pdf.

[29] Kinematic viscosity of air vs. temperature [EB/OL]. 2010-01-24. http:∥bouteloup.pierre.free.fr/lica/phythe/don/air/air_nu_plot.pdf.

[30] LAUTENBERGER C, FERNANDEZ-PELLO C A. Generalized pyrolysis model for combustible solids[C]∥Fire Safety Science-Proceedings of the 8th International Symposium. Beijing: The International Association for Fire Safety Science, 2005: 445-456.

[31] LI J. A multiscale approach to parameterization of burning models for polymeric materials [D]. Maryland: College Park, University of Maryland, 2014.

Numerical simulation of pyrolysis of PMMA involving surface and in-depth absorption

GONG Jun-hui1, CHEN Yi-xuan1, LI Jin2, ZHOU Yang3

(1.CollegeofSafetyScienceandEngineering,NanjingTechUniversity,Nanjing211816,China;2.DepartmentofFireScience,UniversityofNewHaven,WestHaven06516,UnitedStates;3.DepartmentofFireProtectionEngineering,CentralSouthUniversity,Changsha410075,China)

The effects of absorption models on the gasification process of PMMA exposed to an incident heat flux were investigated. A numerical one-dimension model was established to analyze the influence of absorption mode, including surface and in-depth absorption, on pyrolysis process of clear PMMA sample which was exposed to an external heat flux. The corresponding cone calorimetry tests in nitrogen atmosphere that were conducted by the developed model. Some important simulation results were discussed, including mass loss rate, top and bottom surface temperature, temperature distribution in solid. The capability of the model was verified by the comparison between experimental and simulation results. Results showed that some detailed behaviors of the thermal degradation were significantly affected by the absorption modes, like temperature in solid, top surface temperature and initiation of pyrolysis etc. Both hypotheses were acceptable within predicting bench scale experiments．

PMMA; thermal degradation; in-depth absorption; surface absorption

2015-10-11.

国家自然科学基金青年基金资助项目(51506081); 江苏省自然科学基金资助项目(BK20150954); 中国科技大学火灾科学国家重点实验室开放课题资助项目(HZ2015-KF09).

龚俊辉(1986—),男,讲师,博士,从事聚合物材料热解及火蔓延的研究.ORCID: 0000-0003-0101-7448.

E-mail: gjh9896@njtech.edu.cn

10.3785/j.issn.1008-973X.2016.10.007

X 932

A

1008-973X(2016)10-1879-10

浙江大学学报(工学版)网址： www.zjujournals.com/eng