El-Nabulsi模型下基于非标准Lagrange函数的动力学系统的Lie对称性与守恒量

周小三，张毅

（1.苏州科技大学数理学院，江苏苏州215009；2.苏州科技大学土木工程学院，江苏苏州215011）

El-Nabulsi模型下基于非标准Lagrange函数的动力学系统的Lie对称性与守恒量

周小三1，张毅2*

（1.苏州科技大学数理学院，江苏苏州215009；2.苏州科技大学土木工程学院，江苏苏州215011）

研究El-Nabulsi模型下基于非标准Lagrange函数的动力学系统的Lie对称性与守恒量。提出了基于非标准Lagrange函数的变分问题，得到了系统的Euler-Lagrange方程；由广义加速度的不变性，给出了基于非标准Lagrange函数的满足Lie对称性的确定方程，建立了结构方程与守恒量；并举例说明。

非标准Lagrange函数；Lie对称性；守恒量；El-Nabulsi模型

1979年，Lutzky[1]将Lie理论应用于动力学系统的运动微分方程，开始研究力学系统的Lie对称性与守恒量。赵跃宇[2]将Lie对称性理论拓展到非保守力学系统。梅凤翔教授在其著作[3]中详细地研究了约束力学系统的Lie对称性和守恒量。张毅[4]研究了非完整约束系统的Lie对称性并给出了由Lie对称性直接导致的守恒量。关于Lie对称性与守恒量的研究已经取得了一系列重要成果[5-7]，但研究尚限于基于标准Lagrange函数的动力学系统。1978年，Arnold在其著作[8]中将基于标准Lagrange函数的系统称为自然动力系统，为研究基于非标准Lagrange函数的动力学系统做了铺垫。相较于标准Lagrange函数，非标准Lagrange函数形式更一般，有指数形式、对数形式等，可能依赖于时间，也可能不依赖于时间。最近发现，这种不规则的函数在量子场论、宇宙学、非线性微分方程等[9-16]领域发挥重要作用。关于非标准Lagrange函数的动力学研究还是开放的课题。

笔者将研究El-Nabulsi模型下基于非标准Lagrange函数的动力学系统的Lie对称性与守恒量。建立了两类非标准Lagrange函数系统的Euler-Lagrange方程，研究系统在无限小变换下的不变性，建立了Lie对称变换的确定方程，给出了结构方程与守恒量。

1 基于指数Lagrange函数的动力学系统的Lie对称性

1.1 Euler-Lagrange方程

假设系统的位形由n个坐标qs（s=1，2，…，n）确定，El-Nabulsi模型下基于指数Lagrange函数的变分问题定义为求积分泛函

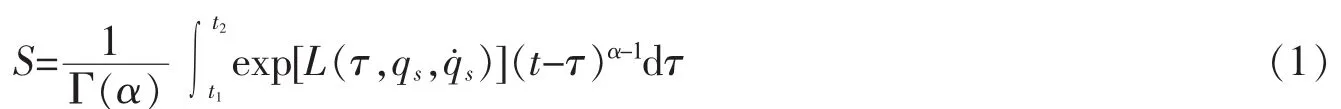
在给定边界条件

上述问题为El-Nabulsi模型下基于指数Lagrange函数的变分问题，泛函（1）为El-Nabulsi模型下基于指数Lagrange函数的Hamilton作用量。

根据变分学理论，有

由式（3），容易得到

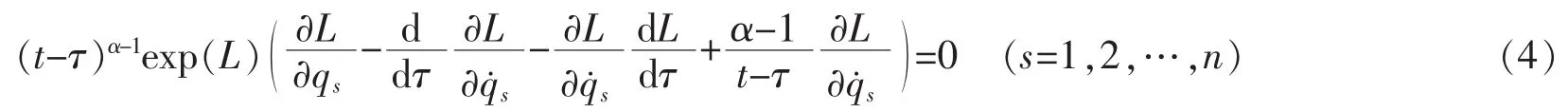
方程（4）称为El-Nabulsi模型下基于指数Lagrange函数的动力学系统的Euler-Lagrange方程。

假设方程（4）非奇异，即

则将式（4）展开可求得广义加速度，记作

1.2 Lie对称性

引进时间和广义坐标的无限小单参数变换群

展开后，有

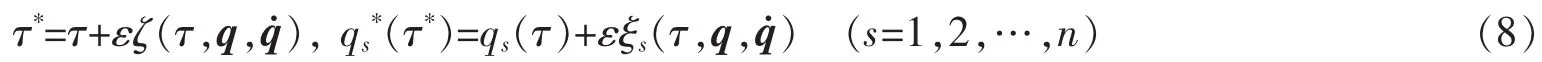
其中ε是无限小参数，ζ和ξs是无限小生成元或称为生成函数。引入无限小生成元向量

式（9）的一次扩展及二次扩展分别为

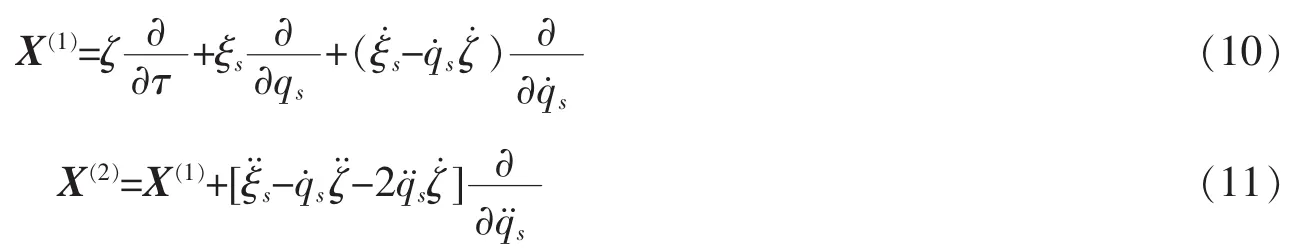
在无限小变换（7）下，方程（6）的不变性归结为满足如下确定方程

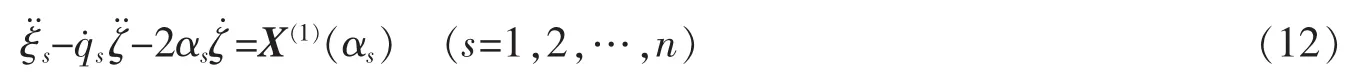
定义1如果生成元ζ和ξs满足确定方程（12），则变换（7）称为El-Nabulsi模型下基于指数Lagrange函数的动力学系统（4）的Lie对称变换。

1.3 结构方程与守恒量

定理1对于El-Nabulsi模型下基于指数Lagrange函数的动力学系统（4），如果无限小生成元ζ，ξs相应于系统的Lie对称性，且存在规范函数G＝G（τ，q，q˙）满足结构方程

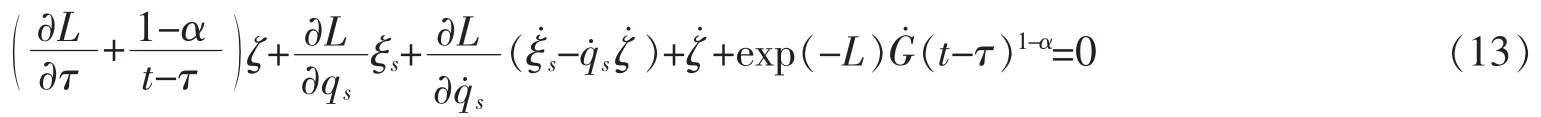
则系统的Lie对称性导致守恒量，形如

证明

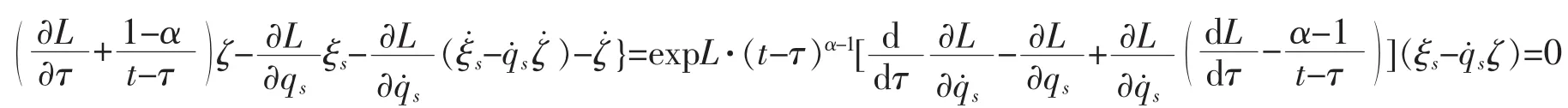
1.4 算例

例1设El-Nabulsi模型下基于指数Lagrange函数的Hamilton作用量为

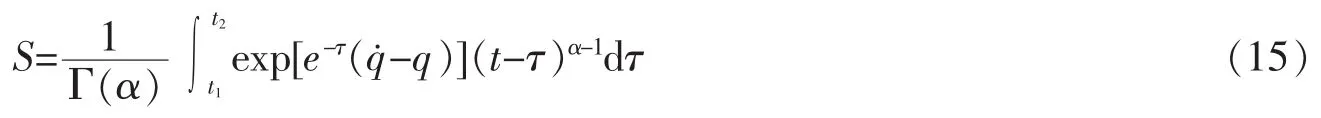
试求系统的Lie对称性与守恒量。

由式（4）得系统的运动微分方程为

根据确定方程（12），有

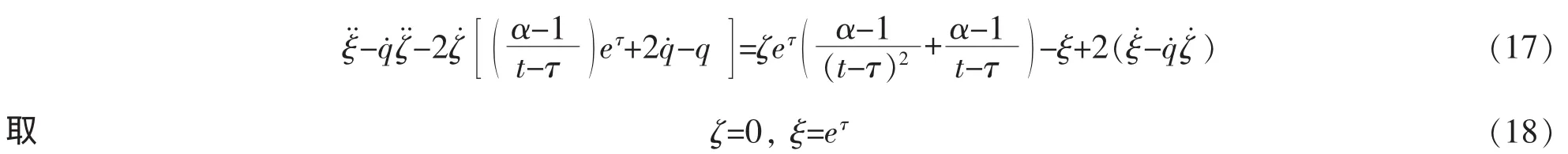
由结构方程（13）得

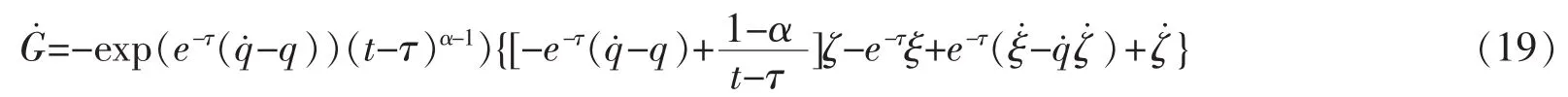
将式（18）代入（19）式，有

式（22）为El-Nabulsi模型下基于指数Lagrange函数的动力系统（16）的Noether型守恒量。

2 基于Lagrange函数幂函数的动力学系统的Lie对称性

2.1 Euler-Lagrange方程

基于Lagrange函数幂函数的动力学系统在El-Nabulsi模型下的变分问题定义为求积分泛函[12]

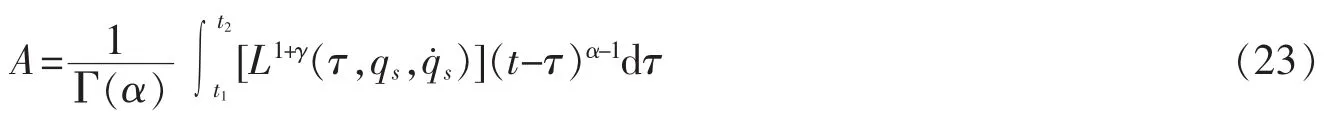
在给定边界条件

上述问题称为El-Nabulsi模型下基于Lagrange函数幂函数的变分问题，泛函（23）为El-Nabulsi模型下基于Lagrange函数幂函数的动力学系统的Hamilton作用量。

根据变分学理论，有

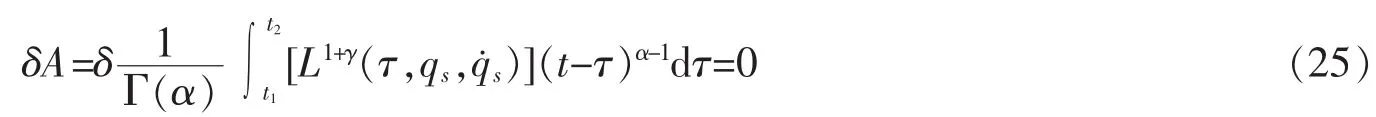
由式（25），容易得到

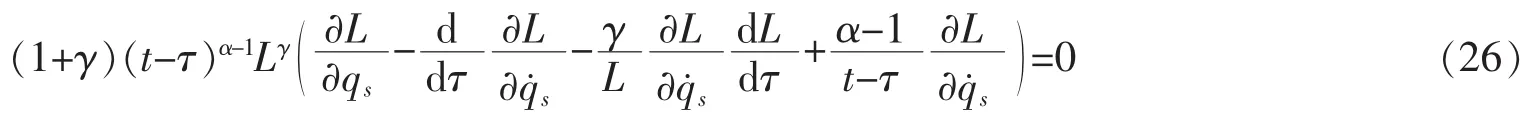
方程（26）称为El-Nabulsi模型下基于Lagrange函数幂函数的动力学系统的Euler-Lagrange方程[12]。

假设方程（26）非奇异，即

则将式（26）展开可求得广义加速度，记作

2.2 Lie对称性

在无限小变换（7）下，方程（28）的不变性归结为满足如下确定方程

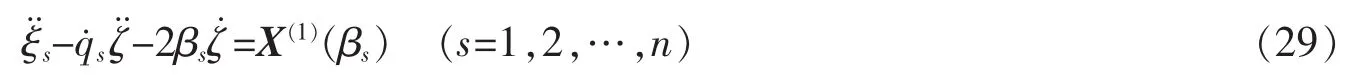
定义2如果生成元ζ和ξs满足确定方程（29），则称变换（7）为基于Lagrange函数幂函数的动力系统（26）的Lie对称变换。

2.3 结构方程与守恒量

定理2对于El-Nabulsi模型下基于Lagrange函数幂函数的动力学系统（26），如果无限小生成元ζ，ξs相应系统的Lie对称性，且存在规范函数满足结构方程

则系统的Lie对称性导致守恒量，形如

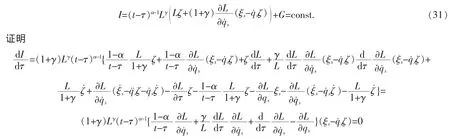
2.4 算例

例2设El-Nabulsi模型下基于Lagrange函数幂函数的Hamilton作用量为

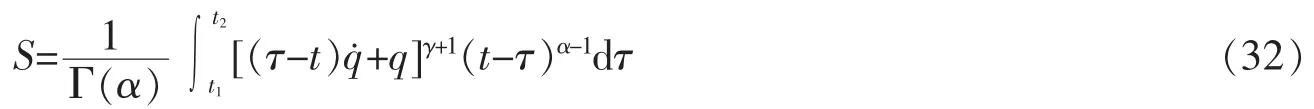
试求系统的Lie对称性与守恒量。

由式（26）得系统的运动微分方程为

取γ＝1时，有

根据确定方程（29），有

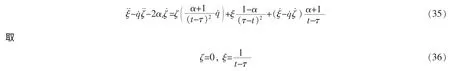
由结构方程（30）得

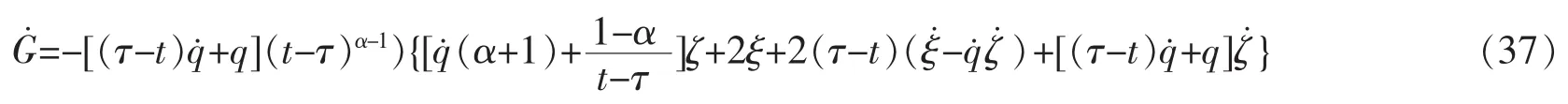
将式（36）代入（37）式，有

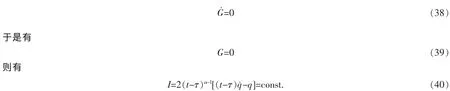
式（40）为El-Nabulsi模型下基于Lagrange函数幂函数的动力学系统（34）的Noether型守恒量。

3 结语

非标准Lagrange函数相对于标准Lagrange函数形式多样，其没有动能与势能的明显区分，可以更好地描述非线性问题[11]，依据非标准Lagrange函数导出耗散系统的运动微分方程[12]更容易。笔者研究了El-Nabulsi模型下基于指数形式与幂函数形式的Lagrange函数的动力学系统的Lie对称性与守恒量。文中方法和结果可进一步推广应用于Hamilton系统、非完整约束系统等，也可进一步研究基于非标准Lagrange函数的动力学系统的Lie对称性导致的Hojman守恒量以及Mei对称性等。

[1]LUTZKY M.Dynamical symmetries and conserved quantities[J].Journal of Physics A：Mathematical and General，1979，12（7）：973-981.

[2]赵跃宇.非保守力学系统的Lie对称性与守恒量[J].力学学报，1994，30（4）：380-384.

[3]梅凤翔.李群和李代数对约束力学系统的应用[M].北京：科学出版社，1999.

[4]ZHANG Y，XUE Y.Conserved quantities from Lie symmetries for nonholonomic systems[J].Journal of Southeast University，2003，19（3）：289-292.

[5]ZHANG Y.Generalized Lutzky conserved quantities of holonomic systems with remainder coordinates subjected to unilateral constraints[J].Communication in Theoretical Physics[J].2006，45（4）：732-736.

[6]HAN Y L，WANG X X，ZHANG M L，et al.Lie symmetry and approximate Hojman conserved quantity of Appell equations for a weakly nonholonomic system[J].Nonlinear Dynamics，2013，71（3）：401-408.

[7]梅凤翔.约束力学系统的对称性与守恒量[M].北京：北京理工大学出版社，2004.

[8]ARNOLD VI.Mathematical Methods of Classical Mechanics[M].New York：Springer，1978.

[9]MUSIELAK Z E.Standard and non-standard Lagrangians for dissipative dynamical systems with variable coefficients[J].Journal of Physics A：Mathematical and Theoretical，2008，41（5）：055205.

[10]MUSIELAK Z E.General conditions for the existence of non-standard Lagrangians for dissipative dynamical systems[J].Chaos，Solitons&Fractals，2009，42（5）：2645-2652.

[11]EL-NABULSIA R.Non-linear dynamics with non-standard Lagrangians[J].Qualitative Theory of Dynamical Systems，2013，12（2）：273-291.

[12]EL-NABULSIA R.Non-standard fractional Lagrangians[J].Nonlinear Dynamics，2013，74（1/2）：381-394.

[13]EL-NABULSIA R.Fractional oscillators from non-standard Lagrangians and time-dependent fractional exponent[J].Computational and Applied Mathematics，2014，33（1）：163-179.

[14]EL-NABULSIA R.Non-standard Lagrangians in rotational dynamics and the modified Navier-Stokes equation[J].Nonlinear Dynamics，2014，79（3）：2055-2068.

[15]EL-NABULSIA R.Quantum field theory from an exponential action functional[J].Indian Journal of Physics，2013，87（4）：379-383.

[16]EL-NABULSIA R.Modified Proca equation and modified dispersion relation from a power-law Lagrangian functional[J].Indian Journal of Physics，2013，87（5）：465-470.Lie symmetries and conserved quantities for dynamical systems with non-standard Lagrangians based on El-Nabulsi models

ZHOU Xiaosan1，ZHANG Yi2
（1.School of Mathematics and Physics，SUST，Suzhou 215009，China；2.School of Civil Engineering，SUST，Suzhou 215011，China）

We studied the Lie symmetries and conserved quantities of dynamical systems with non-standard Lagrangians based on El-Nabulsi models.With the proposition of the variational problem with non-standard Lagrangians,we obtained the Euler-Lagrange equations of the system.By the invariance of generalized acceleration, we gave the determining equations of Lie symmetries with non-standard Lagrangians,and established the structure equations and conserved quantities.Finally,two examples were given to illustrate the application of the results.

non-standard Lagrangians；Lie symmetry；conserved quantity；El-Nabulsi model

O316MR（2000）Subject Classification：70H33；70F25

A

1672-0687（2016）04-0013-05

责任编辑：谢金春

2015-07-17

国家自然科学基金资助项目（11272227）

周小三（1990-），女，安徽宿州人，硕士研究生，研究方向：力学中的数学方法。

*通信联系人：张毅（1964-），男，教授，博士，博士生导师，E-mail：zhy@mail.usts.edu.cn。