一类常微分方程的非标准有限差分法

刘明鼎 段素芳 张艳敏

（青岛理工大学琴岛学院，山东 青岛266106）

微分方程是描述自然科学现象的常用工具，因此对微分方程数值求解的相关理论研究一直是各个领域学者的研究热点。采用方法也比较多，目前常采用的数值求解方法主要有有限差分法、谱方法、有限元法、小波法、分解法等方法[1-6]。

非标准有限差分法Mickens在1994出版的文献[7]中进行了详细地描述。该方法主要讨论在构造微分方程的差分格式时，对导数项离散后的分母函数应具有的形式以及非线性项离散后的形式两个问题。目前国内学者对非标准有限差分方法的应用主要有王媛媛利用非标准有限差分法对Logistic方程进行了分析[8],张磊利用非标准有限差分法和参数扰动法讨论了微分方程的求解[9]，秦雯娣讨论了几类偏微分方程非标准有限差分格式解的正性、有界性以及动力学相容性[10]，王倩倩利用非标准有限差分法研究了两类含空间扩散生物模型数值解并研究了数值解的稳态性[11]。本文将利用非标准有限差分法研究两类能量守恒振子方程[7]。能量方程在研究物理、流体力学等方面有着重要的作用，例如研究无粘不可压缩流体以及无粘可压缩流体的运动现象。

1.一类常微分方程的非标准有限差分格式

在满足Hamilton原理下构造如下能量方程的非标准有限差分格式

ω,f,g为常数。

首先考虑

构造Lagrange函数[12]

对（3）式在tn处进行离散得：

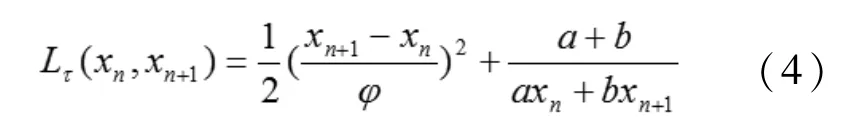
满足性质[12]

根据式（5）计算得a=b。所以有

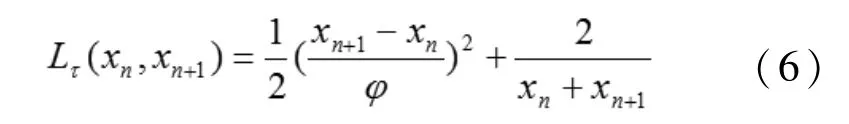
对xn进行移位，利用离散Euler-Lagrange方程[13]，

式(6)满足：

利用式(7)，结合式(6)得：

式(8)为一个二阶非线性差分方程，是(2)式在满足Hamilton原理下的一个非标准有限差分格式。对于式(2)非线性项采用了非局部离散方式为

对于式(2)，传统的有限差分格式为

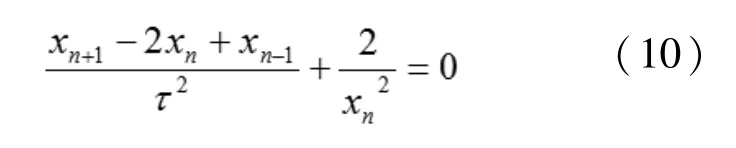
我们再来研究(1)式，采用与(2)式相同的处理过程。构造Lagrange函数

在满足n+1↔n差分格式不变的性质下，对(11)式利用非标准有限差分方法进行离散得

根据式(7)得：

(13)式为(1)式在满足Hamilton原理下的一个非标准有限差分格式。

如果不考虑满足Hamilton原理，可以得到如下的非标准有限差分格式：

利用传统的有限差分方法对(1)式进行离散得

2.一类常微分方程组的非标准有限差分格式

在满足Hamilton原理下构造如下非线性常微分方程组的非标准有限差分格式

对应的Lagrange函数为：

对式(18)进行离散得

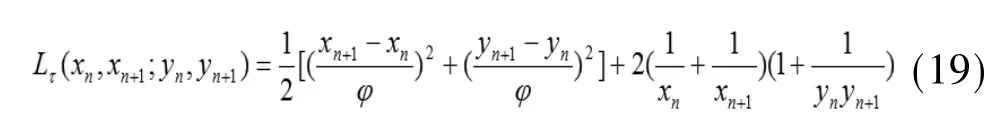
对式(19)中xn,yn进行移位并利用式(7)得

则有

传统的差分格式为

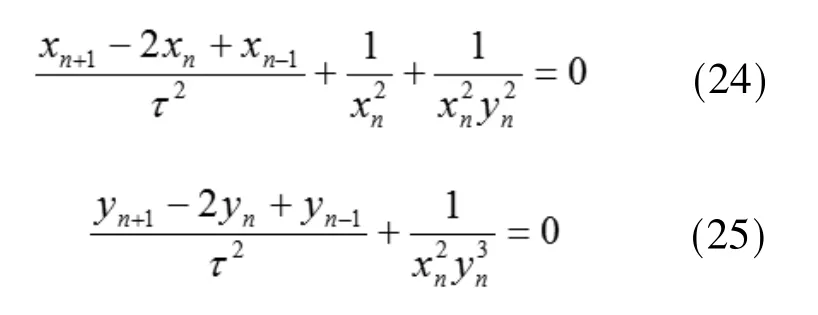
3.非标准有限差分格式性质

性质1 式(8)具有时间转换不变性与能量守恒性[14]。

在式（2）中，令t↔(-t)时，式（2）不变。对应于非标准有限差分格式(8)，令n+1↔n-1，式(8)的格式也不会发生改变。所以式（8）、（13）在不同的相堆成的时间层上具有时间转换不变性与能量守恒性。而传统的有限差分格式（10），在第n+1和n-1和时刻时，差分格式完全不同，所以不具备上述性质。因此利用非标准有限差分方法构造的差分格式可以保持与原微分方程一样的性质，优于传统的有限差分法。

性质2 式（13）具有能量守恒性质。

令n+1↔n-1，带入式（13），得到的差分格式与原差分格式一致，所以式（13）具有能量守恒性，与原微分方程保持同样的性质。而式（14）、（15）则不具备能量守恒性质。

性质3 式（22）、(23)具有能量守恒性质

令n+1↔n-1，带入式（22）、(23)中，变换后的差分格式与变换前的差分格式一致，所以式（22）、(23)具有能量守恒性质，与原微分方程保持同样的性质。对传统的差分格式（24）、（25）做同样的变换，格式上发生了改变，因此不具备能量守恒性质。

4.结语

利用非标准有限差分方法，依据Hamilton原理对一类能量守恒常微分方程和方程组进行离散。对微分方程中的非线性项采用了非局部的离散方式，将离散后的非标准有限差分格式与传统的差分格式进行比较得出，非标准有限差分格式在形式上更复杂，能更好地保留原微分方程能量守恒性质。因此，利用非标准有限差分方法构造的非标准有限差分格式是实用的。