一类二阶差分方程稳定性定理的证明

全卫贞 李晓培

（岭南师范学院基础教育学院，广东 湛江524037）

差分方程知识理论的研究在近二十年来得到了快速的发展。其理论已变成生物学、工程控制、计算机、信息系统、化学和社会经济学中的重要理论依据。它主要来源于连续微分方程的离散化、某些离散方法及各种离散问题（如控制论、生态学、药物动力学）。

在文献[1]中，给出了二阶差分方程渐近稳定性质方面的定理，本文针对其中两个定理给出与其不同的证明方法。此外，我们将方程改成还可以得到另外的两个定理。

1.预备知识

考虑二阶差分方程

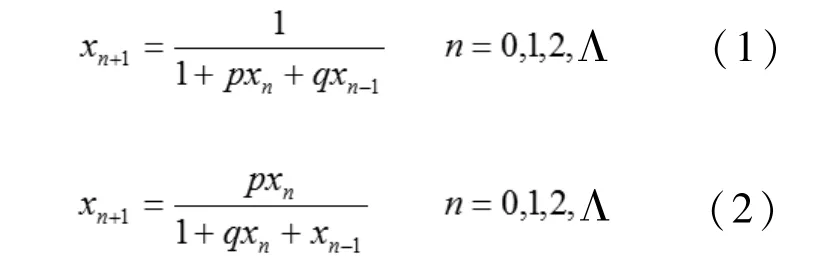
引理1[1]由二阶差分方程得函数f（u，v），令，。若T＜1-＜2，则平衡解是二阶差分方程的局部渐近稳定解。

引理2[1]由二阶差分方程得函数f（x，y），若函数f（x，y）满足下面两个条件：

（1）f（x，y）关于x单调递减，关于y单调递减；

（2）若有f（m，m）=M和f（M，M）=m，则m=M。

引理3[1]由二阶差分方程得函数f（x，y），若函数f（x，y）满足下面两个条件：

（1）f（x，y）关于x单调递增，关于y单调递减；

（2）若有f（m，M）=m和f（M，m）=M，则m=M。

引理4[1]若二阶差分方程为xn+1=f0(xn,xn-1)，xn+f1（xn,xn-1)xn-1满足下面三个条件：

（1）f0（x，y）和f1（x，y）关于x不增，关于y不增；

（2）f0（x，y）＞0（x≥0）；

2.定理及其证明

从文献[1]，我们得到下面的定理1和定理2，并给出与文献[1]不同的证明方法。此证明方法的特点在于先由原差分方程得到函数f(u，v)，从而得到。再根据的情况来判断平衡解的渐近稳定性，其优点是可以适用于判断所有二阶差分方程的平衡解的渐近稳定性。

（2）方程（1）没有素二周期解。

另一方面，因为

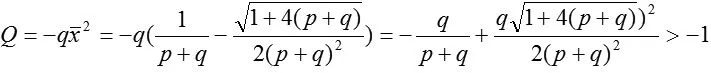
②方法a 反证法，假设方程（1）存在素二周期解，设为Λ，Φ，Ψ，Φ，Ψ，Λ，则

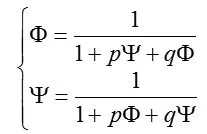
故方程（1）没有素二周期解。

方法b 用文献[1]中的定理，我们也可以判断方程（1）没有素二周期解，具体的证明过程这里将不再赘述。

定理2方程（1）的平衡解是全局渐近稳定的。

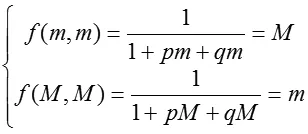
那么m=M，否则p+q=1，与p、q的任意性矛盾。

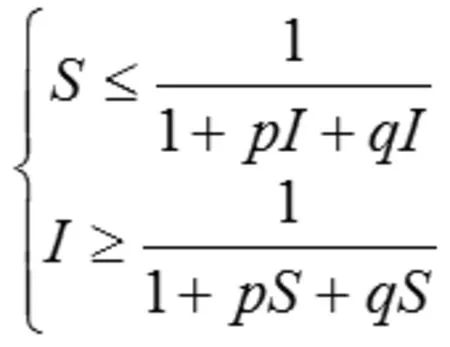
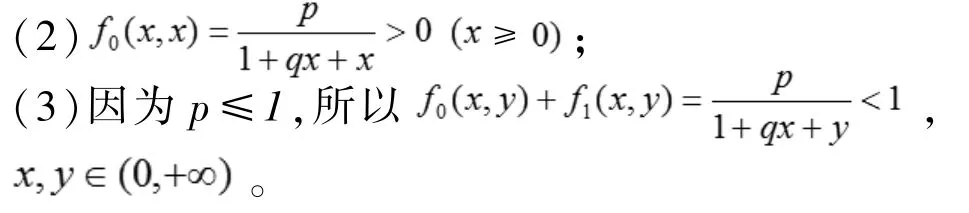
定理4若 p＞1，则方程（2）的正平衡解是全局渐近稳定的。

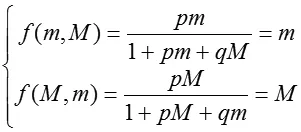
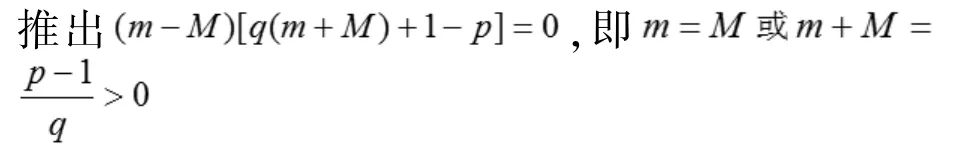
综合之，得m=M。