介观谐振子电路中四模连续变量完美最大纠缠的实现

姜年权， 陈 隆， 刘 祥

(温州大学，浙江 温州 325035)



介观谐振子电路中四模连续变量完美最大纠缠的实现

姜年权， 陈 隆， 刘 祥

(温州大学，浙江 温州 325035)

本文我们将基于连续变量EPR纠缠态以及分束器算符的理论表达式提出四模连续变量完美最大纠缠态(CV PMES)的理论表达形式，在此基础上，进一步利用超导介观LC谐振子电路通过射频超导量子干涉仪进行耦合的系统，提出在实验上近似实现四模连续变量完美最大纠缠态的理论实现方案.

连续变量纠缠态；LC谐振子；超导量子干涉仪

纠缠态是量子通讯和量子计算的基本资源.近年来，人们对不同类型的纠缠态进行了深入的研究和探索，其中一些纠缠态的相关研究已经相当成熟.部分纠缠态可以在离散变量(DV)系统和连续变量(CV)系统中都能够制备出来，例如，我们所熟知的cluster态，开始是在量子比特系统[1,2]中引入的，后来Menicucci和zhang等人[3,4]将它延伸到连续变量系统中.类似的还有GHZ态，Braunstein和Loock等人[5]将它从量子比特系统扩展到了CV系统.但是，还有一些类型的纠缠态，比如完美最大纠缠态(PMMES)等，人们还没能够很好地理解和掌握，它们在DV系统和CV系统中存在着差异.Facchi等人[6]在量子比特系统中引入完美最大纠缠态,初步证明了在量子比特系统中，量子比特数N=4和N≥8时都不存在这种纠缠态.然而，在CV系统中，任意N模的这种纠缠态则有可能存在[7].对于CV PMMES中的四模情况，我们可以在光学系统中得到近似的证明.

在实验上，由于光学系统的连锁反应，操作和探测具有高效性，所以CV纠缠态的近似实现通常采用光学系统[7].然而利用光来研究CV量子态也存在着一些缺点.众所周知，由于光总是以高速传播，所以光学CV量子态只能存在短暂的瞬间而不能持续一段较长的时间.并且光量子信息的存储和读取并不容易，高压缩光(超过10dB)在技术上也很难获得.因此，人们很希望能找到一个拥有光学系统的优点而又没有其缺点系统来用于CV量子态的研究.固态超导量子电路系统(SQC)就是一个很有前景的系统.目前人们对SQC 已经进行了深入的研究[10-16]，其中，已证明超导微波谐振器具有相对高的品质因数，并且可以与各种超导量子比特[17]之间进行强耦合.

本文中，我们首先提出四模CV PMME的一般表达式，进而在SQC中利用超导谐振器经过可控的射频超导量子干涉仪(rf SQUID)耦合来实现CV PMME.我们的方案有以下几个优点：(1)系统能获得高压缩度的量子态,系统中纠缠态能够持续足够长的时间，有利于观察、测量以及操作；(2)量子信息的存储和读取方便；(3)电谐振器耦合的时候同时能够被测量，因此可以提供更多的耦合系统的量子行为.此外，我们的系统拥有固态电路QED的一般优点.

1 完美最大纠缠态的概念

对于量子比特系统而言，Paolo Facchi等人[6]提出了一种完美最大纠缠态，并证明在量子比特系统中，量子比特数N=4或者N≥8都不存在这种纠缠态.下面以量子比特系统来介绍这种纠缠态.

一个由n个qubits粒子S={1,2,3,…,n}组成的希尔伯特空间H=(C2)⊗n，它的态可以表示为

(1)

其中k=(ki)i∈S，ki∈Z2={0,1}

(2)

对于A:

(3)

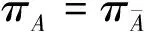
1/NA≤πA≤1

(4)

现在我们来计算πA,式子(1)可以写作

(5)

把式(5)代入到式(3)可得：

(6)

通过分析我们知道，式(6)很容易达到1/NA，如果一个量子态它的任意约化密度算符ρA=1/NA，我们就将它称作完美最大纠缠态.

然而，对于连续变量系统而言，情况有所不同，连续变量系统的量子数是连续变化的，取值范围可以是从-∞到∞.Jing Zhang等人[Phys. Rev. Lett. 103, 070501 (2009)]给出了连续变量系统中完美最大纠缠态的等价定义.

一个n模量子态，将其任意分为的A、B两部分，其中A部分包含有k个模(不妨假设k≤n/2),如果总能通过局域变换将其变为k个EPR对的直积，则该量子态为连续变量完美最大纠缠态.以该量子态作为量子通道，总可以将任意k模的量子态在A、B之间实现保真度为1的量子传输.不过，这种量子态是一种理想的量子态，对应着能量无穷大的情形，实际情况下是无法完全实现的，我们只能在实验上近似实现.

2 四模连续变量完美最大纠缠态的理论表达式

(7)

(8)

(9)

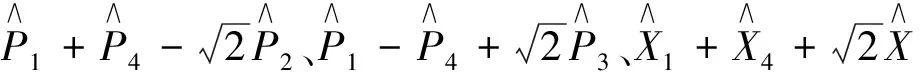
我们也可以把公式(9)改写为

(10)

3 四模连续变量完美最大纠缠态的近似实现

我们用如图1的装置来近似实现四模连续变量完美最大纠缠态.

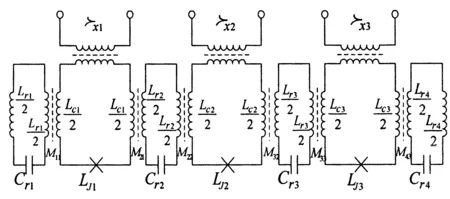
图1 四个LC谐振器与三个射频超导量子干涉器相互耦合Fig.1 Circuit diagram for the lumped-element electrical resonators interact via rf SQUID-mediated tunable couplers

耦合相互作用强度

(11)

其中ωj和ωk是谐振器j和k的频率.

因此，我们可以获得谐振器j和k之间的相互作用

(12)

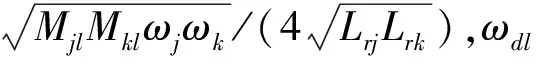
(13)

其中，θ(t1)=λjkt1/ћ.

(14)

(15)

这样，我们就近似实现了四模 CV PMES[24-29].

4 方案的可行性分析及结论

以下用实际参数证明我们的方案的可行性.对于典型的稀释冷藏库的温度约为30mK，我们选择谐振器的频率为10GHz左右，最终谐振器将在基态冷却，因此我们很容易能够制备这些模的压缩态.对于耦合的电谐振器，我们从集成的量子电路[25,31]中选择合理的参数：

ωj/2π=9GHZ，j=1,3,ωk/2π=10GHz,k=2,4

Lj=Lk=5Lc=5Mjl=5Mkl=500pH,I01=2.8μA

本文中我们给出了四模连续变量完美最大纠缠态的一般表达式，提出了在电路QED系统中，利用LC谐振器与rf SQUID耦合来近似产生四模连续变量完美最大纠缠态的方案，该方案在当前技术条件下是可行的.态的纠缠度取决于电路和驱动的参数.与之前大多数应用光学、腔或者原子系统的方案不同，我们在固态电路QED系统中产生了连续变量.

[1] RAUSSENDORF R， BRIEGEL H J. A one-way quantum computer[J]. Phys Rev Lett, 2001,86:5188.

[2] BRIEGEL H J， RAUSSENDORF R. Persistent entanglement in arrays of interacting particles[J]. Phys Rev Lett, 2001,86:910.

[3] MENICUCCI N C et al. Universal quantum computation with continuous-variable cluster states[J]. Phys Rev Lett, 2006,97:110501.

[4] ZHANG J， BRAUNSTEIN S L. Continuous-variable gaussian analog of cluster states[J]. Phys Rev A, 2006,73:032318.

[5] LOOCK P VAN， BRAUNSTEIN S L. Multipartite entanglement for continuous variables: a quantum teleportation network[J]. Phys Rev Lett, 2000,84:3482.

[6] FACCHI P et al. Maximally multipartite entangled states[J]. Phys Rev A, 2008,77:060304(R).

[7] ZHANG J, ADESSO G, XIE C, PENG K. Quantum teamwork for unconditional multiparty communication with gaussian states[J]. Phys Rev Lett, 2009,103:070501.

[8] BRAUNSTEIN S L， KIMBLE H J. Dense coding for continuous variables[J]. Phys Rev A, 2000,61:042302.

[9] TYC T， SANDERS B C. How to share a continuous-variable quantum secret by optical interferometry[J]. Phys Rev A, 2002,65:042310.

[10] CLARKE J， WILHELM F K. Superconducting quantum bits[J]. Nature (London), 2008,453:1031.

[11] BYLANDER J, GUSTAVSSO S, YAN F, et al. Noise spectroscopy through dynamical decoupling with a superconducting flux qubit[J]. Nat Phys, 2011,7:565.

[12] DE GROOT P C, LISENFELD J, SCHOUTEN R N, et al. Selective darkening of degenerate transitions demonstrated with two superconducting quantum bits[J]. Nat Phys, 2010,6:763.

[13] DEPPE F, MARIANTONI M, MENZEL E P, et al. Two-photon probe of the Jaynes-Cummings model and controlled symmetry breaking in circuit QED[J]. Nat Phys, 2008,4:686.

[14] MARIANTONI M, WANG H, YAMAMOTO T, et al. Implementing the quantum von neumann architecture with superconducting circuits[J]. Science, 2011,334:61.

[15] DICARLO L, REED M D, SUN L, et al. Preparation and measurement of three-qubit entanglement in a superconducting circuit[J]. Nature (London), 2010,467:574.

[16] MALLET F, ONG F R, PALACIOS-LALOY A, et al. Single-shot qubit readout in circuit quantum electrodynamics[J]. Nat Phys, 2009,5:791.

[17] SCHOELKOPF R J， GIRVIN S M. Wiring up quantum systems[J]. Nature (London) 2008,451:664.

[18] YOU J Q， NORI F. Atomic physics and quantum optics using superconducting circuits[J]. Nature (London)， 2011,474:589.

[19] HOFHEINZ M, WANG H, ANSMANN M, et al. Synthesizing arbitrary quantum states in a superconducting resonator[J]. Nature (London) 2009,459:546.

[20] ZAKKA-BAJJANI E, NGUYEN F, LEE M, et al. Quantum superposition of a single microwave photon in two different ‘colour’ states[J]. Nat Phys, 2011,7:599.

[21] WANG H, MARIANTONI M, BIALCZAK R C, et al. Deterministic Entanglement of Photons in Two Superconducting Microwave Resonators[J]. Phys Rev Lett, 2011,106:060401.

[22] HU Y AND TIAN L. Deterministic Generation of Entangled Photons in Superconducting Resonator Arrays[J]. Phys Rev Lett, 2011,106:257002.

[23] STRAUCH F W, JACOBS K, SIMMONDS R W. Arbitrary control of entanglement between two superconducting resonators[J]. Phys Rev Lett, 2010,105:050501.

[24] VAN DEN BRINK A M, BERKLEY A J， YALOWSKY M. Mediated tunable coupling of flux qubits. New J Phys, 2005,7:230.

[25] TIAN L, ALLMAN M S， SIMMONDS R W. Parametric coupling between macroscopic quantum resonators. New J Phys, 2008,10:115001.

[26] KIMBLE H J. The quantum internet[J]. Nature (London), 2008,453:1023.

[27] MENICUCCI N C, VAN LOOCK P, GU M, et al. Universal quantum computation with continuous-variable cluster states[J]. Phys Rev Lett, 2006,97:110501.

[28] FAN H Y， VANDERLINDE J. Simple approach to the wave functions of one- and two-mode squeezed states[J]. Phys Rev A, 1989,39:1552.

[29] MCDERMOTT R, SIMMONDS R W, STEFFEN M, et al. Simultaneous state measurement of coupled josephson phase qubits[J]. Science, 2005,307:1299.

[30] LI P B, GAO S Y, LI F L. Engineering two-mode entangled states between two superconducting resonators by dissipation[J]. Phys Rev A, 2012,86:012318.

Perfect Maximally Quadruple Entanglement and Its Implementing in Solid-State Quantum Circuit

JIANG Nian-quan, CHEN Long, LIU Xiang

(School of Physics and Electric Information, Wenzhou University, Wenzhou 325035, China)

In this paper, we proposed a way to obtain continuous-variable perfect maximally quadruple entangled states by applying beam splitter operations on continuous-variable EPR states. Then we show that the approximate version of these states can be achieved in circuit quantum electrodynamics systems composed of LC superconducting resonators and rf SQUIDs by tuning the applied flux bias to the rf SQUIDs.

Continuous-variable entangled states； LC resonators； rf SQUIDs

2016-04-07

国家自然科学基金(60710947017/A05).

姜年权(1966-)，男，安徽太湖县人，教授，研究生导师.

10.14182/J.cnki.1001-2443.2016.05.001

TN929.11

A

1001-2443(2016)05-0409-05