一维电谐振子能量本征问题的代数解法研究①

乔流飞，赵晓东，裴魏魏,*，张海丰

(1.佳木斯大学理学院，黑龙江 佳木斯 154007；2.延边大学护理学院，吉林 延吉 13300)

0 引 言

在量子力学中一维电谐振子是重要的模型系统中的一者，任意势在稳定平衡点附近可以用谐振子势来近似。谐振子是存在简单解析解的量子系统，量子谐振子可用来近似描述分子运动，所以对于谐振子的解的研究就格外重要。例如：肖奎等对一维线性谐振子波函数及概率分布的可视演示[1]；张小伟给出了关于电场中线性谐振子问题的求解[2]；赵清锋用待定系数法求解一维线性谐振子在微扰体系下的解析解[3]；此外还有对二维谐振子、谐振子的概率密度与时间的关系、同调谐振子谱空间上的对称性和参量双粒子模型等方面的研究[4-10]。利用精确解、升降算符等方法求解一维电谐振子的能级和波函数。

1精确解方法

设一维线性谐振子带有电荷为q，哈密顿算符为

(1)

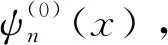
(2)

将式(2)中势能项作如下变形

(3)

其中x0=qε/mω2。

令

x′=x-x0，

(4)

则哈密顿算符变为

(5)

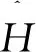
(6)

波函数为

(7)

一维线性谐振子的能级为

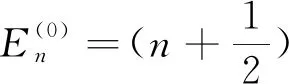
(8)

其中n=0,1,2,…。因此

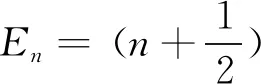
(9)

2 升降算符方法

下面采用升降算符的方法求解上边的一维电谐振子的问题。令

(10)

(11)

则

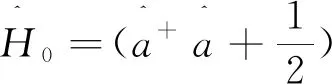
(12)

(13)

其中x0=qε/mω2。

则

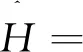
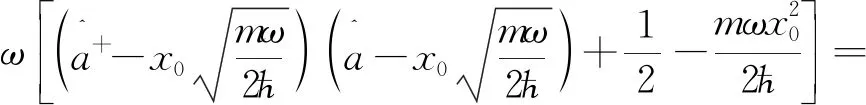
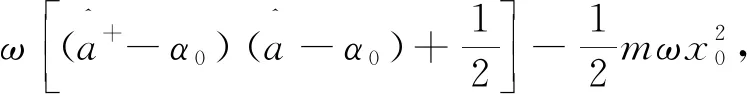
(14)

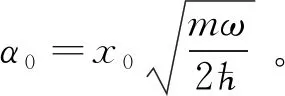
根据对易关系

(15)

可得

(16)

(17)

且

(18)

由于

(19)

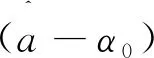
(20)

(21)

(22)

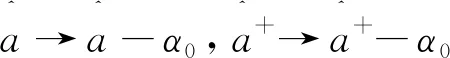
φn(x)=ψn(x-x0)=Dx(x0)ψn(x)，

(23)

其中Dx(x0)为平移算符。φn(x)和φ0(x)的关系为

(24)

3 近似解方法

对于上边的同一问题我们还可以才有微扰理论，进行近似求解

(25)

(26)

(27)

则

(28)

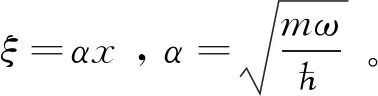
(29)

根据微扰理论公式可得

(30)

(31)

(32)

所以

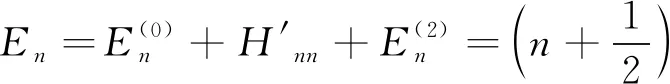
(33)

4 任意时刻的体系波函数

设0≤t≤τ时给一维线性谐振子施加均匀电场ε。设t=0时体系处于基态ψ0(x)，下边求t>τ时的ψ(x,t)。t=0时，波函数满足

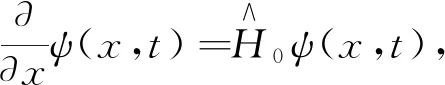
(34)

可以解得

(35)

其中展开项系数为

|<ψn|ψ>|2=|fn|2,

(36)

t=τ时

(37)

所以以下通过求ψ(x,τ)来确定fn。

0≤t≤τ时的薛定谔方程为

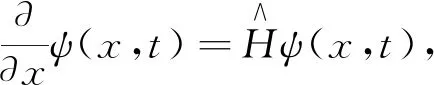
(38)

其通解为

(39)

其中展开项系数Cn由初始波函数给出，即

(40)

根据平移操作的性质可得

ψ0(x)=φ0(x+x0)=Dx(-x0)φ0(x)，

(41)

其中x0=qε/mω2。由升降算符表示的平移操作算符Dx(-x0)为

(42)

根据Glauber公式

(43)

可以得到

(44)

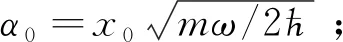
(45)

(46)

(47)

所以

(48)

(49)

可见ψ0(x)用φn的基矢组成的相干态表示出来了。于是

(50)

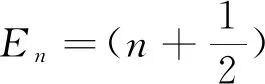
(51)

(52)

其中α(τ)=α0e-iωτ，

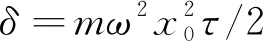
(53)

所以ψ(x,τ)表示为

(54)

(55)

(56)

于是可以用ψn表示ψ(x,τ)，利用公式

(57)

可得

(58)

式中ψn向ψ(x,τ)的系数为

(59)

易知

(60)

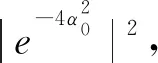
(61)

5 结 语