一种基于位置信号线性拟合差分滤波器串联的二阶差分角加速度观测器
邱文彬, 柴建云, 孙旭东, 陆海峰, 樊明
(清华大学 电机系电力系统国家重点实验室,北京 100084)
一种基于位置信号线性拟合差分滤波器串联的二阶差分角加速度观测器
邱文彬, 柴建云, 孙旭东, 陆海峰, 樊明
(清华大学 电机系电力系统国家重点实验室,北京 100084)
角加速度闭环能增加伺服控制系统的刚度,提高系统鲁棒性,但位置信号的二阶差分运算会放大高频噪声幅值,限制了加速度闭环在实际控制中的应用。首先,对三种基于多项式曲线拟合的角加速度观测器性能进行了分析,结果表明二次多项式角加速度观测器具有最优的综合性能;其次,为了抑制噪声,提出了一种基于位置信号线性拟合的串联二阶差分角加速度观测器,从截止频率、白噪声放大倍数和延时时间三个方面对其性能进行了分析,并与二次多项式角加速度观测器进行了对比,仿真和实验均验证了该方法具有更好的噪声抑制能力。
角加速度; 多项式曲线拟合; 角加速度观测器; 串联二阶差分观测器; 高频噪声
0 引 言
工业机器人是一个多轴强耦合、时变非线性的控制系统,它的参数和负载扰动会随着位姿变化而改变,导致经典三环伺服控制系统的性能变差。角加速度闭环可以增加系统的鲁棒性,提高系统对参数变化以及负载扰动的抑制能力[1-2]。在一些先进控制方法,如滑模变结构控制、扰动观测器[3-4],也需要使用角加速度信号。由于高性能伺服系统大多配置有位置传感器,角加速度主要通过位置信号的二阶差分运算间接观测得到[5],但位置信号的直接二阶差分运算会放大高频噪声幅值,给准确观测带来困难。
针对该问题,国内外众多学者进行了深入研究。文献[6-8]对几种多项式拟合的一阶差分速度观测器进行了研究,将其与基于Taylor级数的一阶差分速度观测器和基于后向差分法的一阶差分速度观测器进行了对比分析,结果表明线性拟合一阶差分速度观测器有更好的噪声抑制能力。文献[9]验证了多项式曲线拟合二阶差分角加速度观测器比直接的二阶差分法角加速度观测器有更好的噪声抑制性能。为了减小多项式曲线拟合差分观测器的延时时间,文献[10-11]提出通过多项式模型对差分输出进行预测,但该方法使观测器的噪声抑制能力变差。为了获得更好的噪声抑制能力,文献[13]提出基于单维卡尔曼滤波器的角加速度观测器,但卡尔曼滤波器特征值的设计一直是难点。为了在抑制噪声和延时时间获得更好的综合性能,文献[14]使用基于单维卡尔曼滤波器的角加速度观测器和二阶牛顿预测器的串联来实现角加速度的观测,该方法虽然减少了延时时间,但同时也削弱了噪声抑制能力。文献[15]提出用优化的IIR一阶差分观测器与多项式曲线拟合一阶差分观测器的串联来实现角加速度观测,该方法有效抑制了噪声,但优化函数构造复杂,且没有分析延时时间。文献[16]提出构建基于模型的全阶观测器来提高观测角加速度的响应速度,但没有对噪声抑制性能进行分析,另外,全阶观测器极点的设计需要依赖经验,性能受模型精度的影响。为了加快角加速度观测值的收敛速度,文献[17-18]使用非线性反馈来构造角加速度观测器,但非线性反馈会引入高频噪声,且难以定量分析观测器的噪声抑制能力。
因为缺乏统一的衡量指标,上述文献没有对提出的角加速度观测器进行定量分析。本文提出从观测器的噪声抑制能力、信号跟踪能力以及频率延时三个方面来衡量二阶差分角加速度观测器的性能,并从噪声抑制能力和延时时间两个方面对各种角加速度观测器进行了对比分析。
从上述文献分析可以看出,基于最小二乘的多项式曲线拟合二阶差分角加速度观测器具有波形不失真、噪声抑制能力强的特点。本文主要针对基于最小二乘的多项式曲线拟合二阶差分角加速度观测器进行研究,首先,对几种多项式曲线拟合角加速度观测器的性能进行了定量的对比分析;其次,为了提高噪声抑制能力,提出了一种基于线性拟合一阶差分滤波器串联来实现角加速度观测的方法,将其与综合性能最优的多项式曲线拟合二阶差分观测器进行对比分析,通过仿真和实验验证了所提方法的有效性。
1 低通二阶差分角加速度观测器的性能评价指标
理想低通二阶差分观测器的幅频特性曲线如图1所示,理想输出相位为180°。
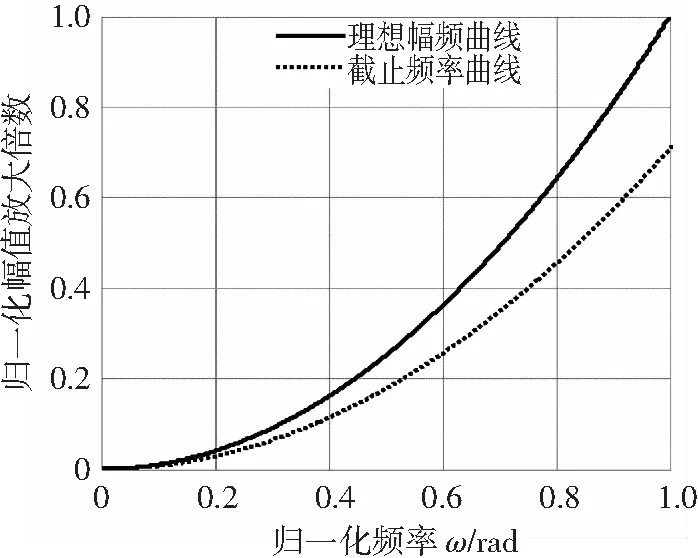
图1 理想低通二阶差分观测器的幅频特性曲线
Fig. 1 Magnitude-frequency characteristic curve of the ideal 2nddifferential observer
角加速度观测器的主要性能应包括信号跟踪能力、噪声抑制能力和延时时间,由于传统的截止频率只能表示对输入信号的跟踪能力,不能描述阻带内的噪声抑制能力,提出用截止频率、白噪声放大倍数和频率延时三个指标来综合衡量二阶差分角加速度观测器的性能,它们的定义如下:

2) 白噪声放大倍数,由于白噪声在频域内为平谱,白噪声放大倍数表示整个频带内信号的放大能力,当数字滤波器的传递函数如下所示时:

根据Parse Val定理,数字滤波器的白噪声放大系数K为:
(1)
3)频率延时,观测器的延时时间对系统的稳定性和控制系统的性能有非常重要的影响。由于中心对称型FIR滤波器具有线性相频特性,不同频率的延时时间相同,输出波形不失真,用延时时间来表示频率延时。
截止频率表示观测器的信号跟踪能力;噪声抑制能力指观测器在高于截止频率段的噪声抑制能力,在截止频率相同时,白噪声放大倍数可以表示观测器的噪声抑制能力;延时时间表示观测器输出值与实际值的延时时间。
2 串联式角加速度观测器
线性拟合一阶差分速度观测器比多项式拟合一阶差分速度观测器有更好的滤波性能[6],但线性拟合曲线的二阶差分为零,无法从线性拟合曲线直接获取二阶差分值,为了获得更好的噪声抑制性能,提出用两个线性拟合一阶差分滤波器串联来实现二阶差分角加速度的观测。基于串联线性拟合差分滤波器的二阶差分角加速度观测器简称为串联式角加速度观测器,基于多项式曲线拟合的二阶差分角加速度观测器简称为多项式角加速度观测器。
当串联式角加速度观测器为(2N+1)阶时,观测器的延时时间为N个数据周期,两个一阶差分滤波器存在多种组合方式,如图2所示,两级差分滤波器的阶数N1、N2间存在如下约束:
N1+N2=N,N≥2。
(2)

图2 串联二阶差分观测器与差分滤波器的阶数关系
Fig. 2 Order relationship between the series 2nddifferential observer and differential filters
由于差分滤波器的串联顺序不改变二阶差分观测器的幅频特性及相频特性,根据式(2)可知,N1的取值区间为[1,N/2],当N1取N/2时具有最好的噪声抑制能力,所提的串联式角加速度观测器指差分滤波器阶数N1取N/2时的串联组合。
2.1 串联式角加速度观测器系数计算
基于最小二乘的线性拟合一阶差分滤波器具有最优的白噪声抑制性能[10],线性拟合一阶差分滤波器的传递函数系数计算方法如下:

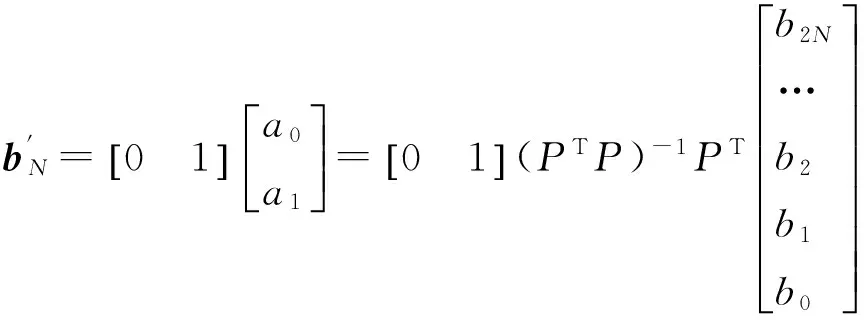
(3)
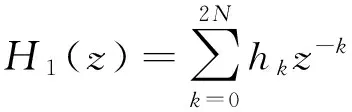
(4)
差分滤波器的系数hk计算表达式如下所示:
(5)
在z域上两个一阶差分滤波器的串联对应为时域上的卷积运算,输入位置信号为(4N+1)个数据点时,串联式角加速度观测器在2N时刻的输出为:

(6)
串联式加速度观测器的传递函数为:
(7)
2.2 串联式角加速度观测器的性能分析
从延时时间、截止频率和白噪声放大倍数三个方面对串联式角加速度观测器和多项式角加速度观测器的性能进行分析如下:
1)延时时间,中心对称型FIR滤波器具有群延时的特性,同阶的多项式加速度观测器与串联式加速度观测器延时时间相同。(4N+1)串联式加速度观测器与(2N+1)差分滤波器的延时时间关系如图3所示,群延时为2N个数据周期。

图3 串联二阶差分观测器与差分滤波器的延时关系
Fig. 3 Delay relationship between the series 2nddifferential observer and the differential filters
2)截止频率,已知一阶差分滤波器阶数时,由式(3)和式(6)可计算得到串联式加速度观测器的传递函数系数,由传递函数系数可得到观测器的截止频率ωc,图4给出了串联式加速度观测器和多项式加速度观测器的延时时间与截止频率的关系。
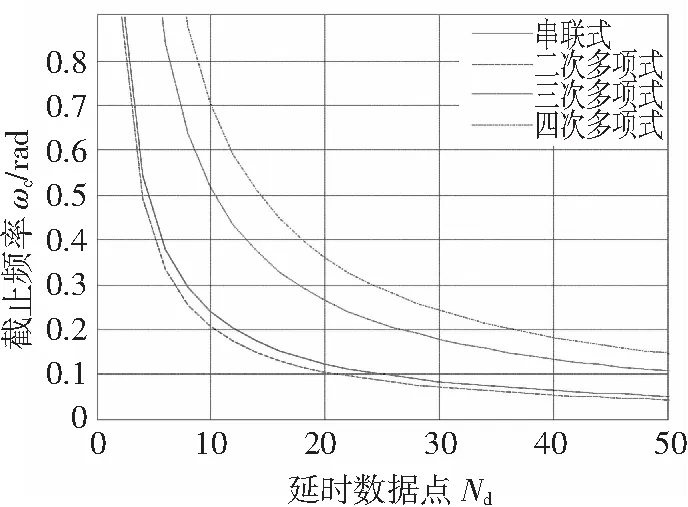
图4 延时数据周期与截止频率的关系
Fig. 4 Relationship between the delay data period numbers and the cut-off frequency
3)白噪声放大倍数,将加速度观测器传递函数的系数代入式(1)可计算得到加速度观测器的白噪声放大倍数K,图5给出了串联式二阶差分观测器和多项式二阶差分观测器的延时时间与白噪声放大倍数的关系。

图5 延时数据周期与白噪声放大倍数的关系
Fig. 5 Relationship between the delay data period numbers and the noise magnification
在延时时间相同时,串联式二阶差分观测器与多项式拟合二阶差分观测器的截止频率与白噪声放大倍数的关系如图6所示。
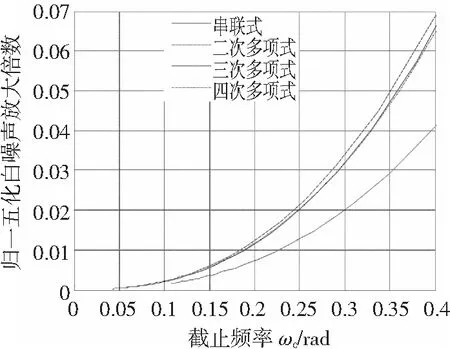
图6 截止频率与白噪声放大倍数的关系
Fig. 6 Relationship between the cut-off frequency and the noise magnification
从图4可以看出,当截止频率相同,三次多项式观测器和四次多项式观测器的延时时间是二次多项式观测器延时时间的2倍左右,而串联式观测器与二项式观测器的延时时间相近;在白噪声放大倍数相同时,从图5可以看出,三次多项式观测器和四次多项式观测器的延时时间是二次多项式观测器延时时间的2倍以上,而串联二阶差分观测器与二次多项式观测器的延时时间较接近;从图6可以看出,不考虑延时时间时,三次多项式观测器的噪声抑制能力最好,二次多项式观测器噪声抑制能力最差,四次多项式观测器和串联式观测器的噪声抑制性能较接近。
从上述分析可以看出,当延时时间相同时,二次多项式观测器和串联式观测器的滤波性能都远优于高次多项式观测器;不考虑延时时间时,高次多项式观测器的噪声抑制性能高于二次多项式观测器和串联式观测器。由于延时时间对控制系统的性能非常重要,所以在多项式观测器中,二次多项式观测器的综合性能远优于其它高次多项式观测器,而串联式观测器与二次多项式观测器的综合性能相近。
3 仿真与实验分析
对串联式角加速度观测器与二次多项式角加速度观测器的性能进行仿真和实验对比分析,实验平台为类PUMA工业机器人的第六臂,输出轴连接有1:100的谐波减速机,仿真和实验的位置信号系统参数如表1所示。

表1 系统参数
由图4、图5和图6可知串联式观测器和二次多项式观测器的性能参数如表2所示。
表2 角加速度观测器的性能参数
Table 2 Angular acceleration performance characteristics

串联式二次多项式观测器阶数N6151截止频率ωc/Hz2727延时时间τ/ms1512.75白噪声放大倍数K0.001320.00145
将观测器的阶数代入式(3)~式(7),可计算得到串联式角加速度观测器的传递函数系数,串联式角加速度观测器的冲激响应如图7所示,51阶二次多项式角加速度观测器的冲激响应如图8所示。
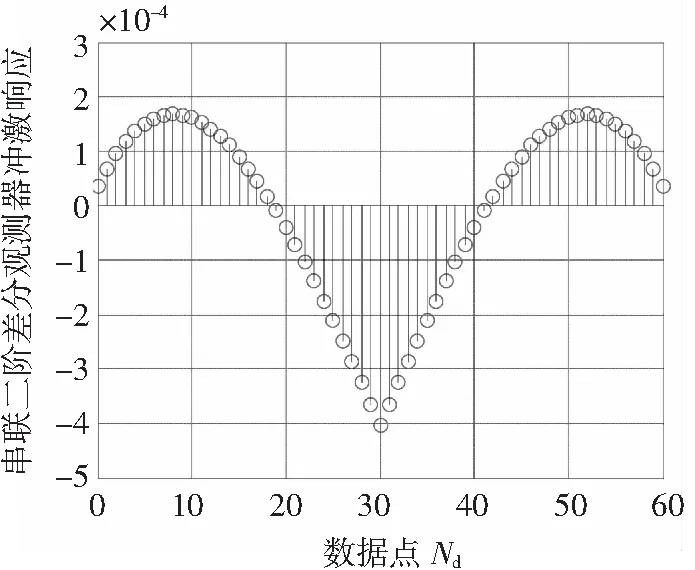
图7 串联二阶差分角加速度观测器的冲激响应
Fig. 7 Impulse response of the series 2nddifferential angular acceleration observer
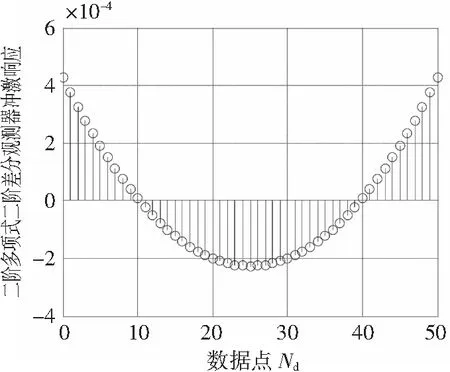
图8 二次多项式角加速度观测器的冲激响应
Fig. 8 Impulse response of the 2nddegree polynomial angular acceleration observer
由测量系统的采样频率fs和归一化后的白噪声放大倍数K可计算出串联式角加速度观测器的白噪声实际放大倍数M1和二次多项式角加速度观测器的白噪声实际放大倍数M2为:
M1=f2sK1=4×106×0.001 32=5 280,
M2=f2sK2=4×106×0.001 45=5 800。
(8)
当参考加速度为±12 rad/s2的方波时,如图9(a)所示,在位置信号中叠加有幅值为0.01°,频率为100 Hz的正弦波噪声,串联式加速度观测器的观测角加速度如图9(b)所示,波动幅度为0.3 rad/s2,二次多项式加速度观测器的输出如图9(c)所示,加速度的波动幅度为3 rad/s2,是串联式加速度观测器波动幅值的100倍,这主要是因为串联角加速度观测器的旁瓣峰值更小,对噪声的抑制能力更强。
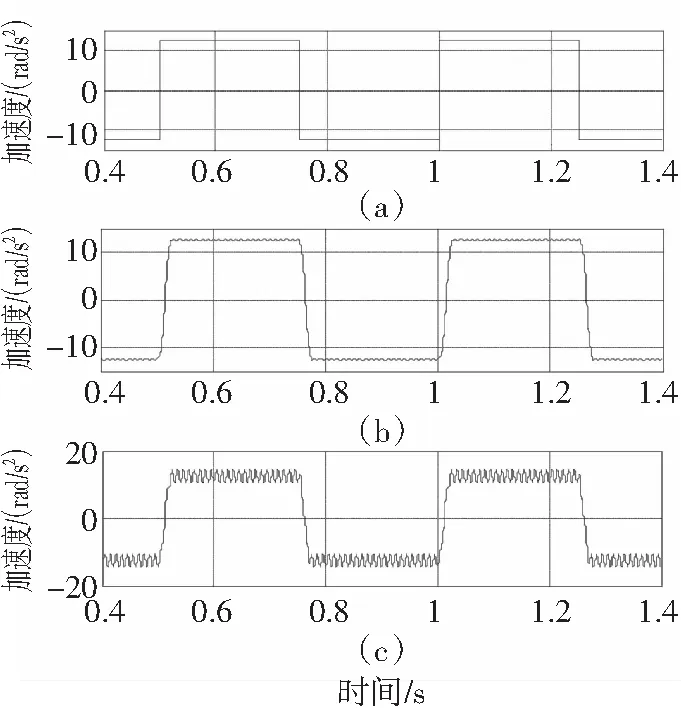
图9 含有正弦噪声时方波加速度的仿真波形
Fig. 9 Simulation waveforms of the square acceleration with the sine noise
实测转速为如图10(a)所示的加减速曲线,串联式角加速度观测器的观测角加速度如图10(b)所示,二次多项式加速度观测器的观测角加速度如图10(c)所示,从图10可以看出,串联式角加速度观测器的高频波动更小,因为二次多项式观测器的白噪声放大倍数比串联式观测器的白噪声放大倍数高11%,串联式角加速度观测器的白噪声抑制能力更强,另外,在转速过零时加速度存在幅值变小的阶跃,这是由于静摩擦力和减速机滞环的影响。

图10 转速为梯形波时的实验波形
4 结 论
针对二阶差分角加速度观测器缺乏统一的性能衡量指标情况,本文首次提出用截止频率、白噪声放大倍数、频率延时综合衡量角加速度观测器的性能,解决了定量分析二阶差分角加速度观测器的问题。在此基础上,对比分析了三种多项式加速度观测器的性能,结果表明二次多项式角加速度观测器具有最优的综合性能。为了提高噪声抑制能力,本文提出了一种基于位置信号线性拟合的串联二阶差分角加速度观测器,将其与二次多项式角加速度观测器进行了对比分析,仿真和实验结果表明,在截止频率相同时,串联二阶差分角加速度观测器噪声抑制能力更好。
[1] HAN J D, WANG Y C, TAN D L, et al. Acceleration feedback control for direct-drive motor system[C]//Intelligent Robots and Systems, 2000. Proceedings of the 2000 IEEE/RSJ International Conference on. IEEE, 2000, 2: 1068-1074.
[2] XU WL, HAN J D. Joint acceleration feedback control for robots: Analysis, sensing and experiments[J]. Robotics and Computer-Integrated Manufacturing. 2000, 16(5): 307-320.
[3] 胡强晖, 胡勤丰. 全局滑模控制在永磁同步电机位置伺服中的应用[J]. 中国电机工程学报, 2011(18):61-66.
HU Qianghui, HU Qinfeng. Global sliding mode control for permanent magnet synchronous motor servo system[J]. Proceedings of the CSEE, 2011(18):61-66.
[4] 张晓光,孙力,赵克. 基于负载转矩观测的永磁同步电机滑模控制[J]. 中国电机工程学服, 2012(3):111-116.
ZHANG Xiaoguang, SUN Li, ZHAO Ke. Sliding mode control of PMSM based on a novel load torque sliding mode observer[J]. Proceedings of the CSEE, 2012(3):111-116.
[5] OVASKA S J, VLIVIITA S. Angular acceleration measurement: A review[C]//Instrumentation and Measurement Technology Conference, 1998. Proceedings of the 1998 IEEE IMTC Conference on. IEEE, 1998, 2: 875-880.
[6] RONALD H B, SUSAN C S, MICHAEL G M. Analysis of algorithms for velocity estimation from discrete position versus time data[J]. IEEE Transactions on industrial electronics. 1992, 2(1): 11-19.[7] CARPENTER PS, BROWN RH, HEINEN JA, et al. On algorithms for velocity estimation using discrete position encoders[C]//Industrial Electronics, Control, and Instrumentation, 1995. Proceedings of the 1995 IEEE IECON 21st International Conference on. IEEE, 1995, 2: 844-849.
[8] PHILLIPS SM, BRANICKY MS. Velocity estimation using quantized measurements[C]//Decision and Control, 2003. Proceedings of the 42nd IEEE Conference on. IEEE, 2003, 5: 4847-4852.
[9] NAGATOMI H, OHNISHI K. Acceleration estimation method for motion control system with optical encoder[C]//Industrial Technology, 2006. Proceedings of the 2006 IEEE ICIT International Conference on. IEEE, 2006: 1480-1485.
[11] ALIVIITA S, VAINIO O. Delayless differentiation algorithm and its efficient implementation for motion control applications[J]. IEEE Trans Instrumentation and Measurement, 1999, 48(5): 967-71.
[12] RJE MERRY, MJG DE M, STENIBUCH M. Velocity and acceleration estimation for optical incremental encoders[J]. Mechatronics, 2010(20):20~26.
[13] PR BELANGER, P DOBROVOLNNY, A HHLMY. Estimation of angular velocity and acceleration from shaft-encoder measurements [J]. The International Journal of Robotics Research, 1998, 17(11): 1225-1233.
[14] 何玉庆, 韩建达. 基于卡尔曼滤波及牛顿预测的角加速度估计方法试验研究[J]. 机械工程学报, 2006(2): 226-232HE Yuqing, HAN Jianda. Experimental study of angular acceleration estimation based on Kalman filter and Newton predictor[J]. Chinese journal of mechanical engineering, 2006, 24(2):22 6-232.
[15] HARRISON AJ, McMahon, C A. Estimation of acceleration from data with quantization errors using control finite-difference methods[J]. Proc Inst. Mech. Engineers 1993, 20(7):77-86.
[16] LORENZ R D, PATTERN KWV. High-resolution velocity estimation for all-digital, ac servo drives[J]. IEEE Transactions on Industrial Applications, 1991, 27(4): 701-705.
[17] 刘咔. 角加速度控制系统研究[D]. 哈尔滨: 哈尔滨工业大学, 2008.
[18] 郑泽东, 李永东, Maurice Fade. 基于扩展Kalman滤波器的PMSM高性能控制系统[J]. 电工技术学报, 2007, 22(10): 18-23.
ZHEN Zedong, LI Yongdong, MAURICE Fadel. High performance PMSM control system based on extended Kalman filter[J]. Transactions of China Electrotechnical society, 2007, 22(10): 18-23.
[19] SEHAN LEE, JAEBOK SONG. Acceleration estimator for low-velocity and low-acceleration regions based on encoder position data[J]. IEEE ASME Trans. on Mechatronics. 2001, 6(1): 58~64.
[20] SULLIGOI G, KAVANAGH RC. An innovative method for improved real-time measurements of angular acceleration in motion control systems[C]//Power Electronics, Electrical Drives, Automation and Motion, 2006. Proceedings of the 2006 IEEE SPEEDAM. International Symposium on, IEEE, 2006: 658~662.
[21] SUJI T T, KOBAYASHI H. Robust acceleration control based on acceleration measurement using optical encoder[C]//Industrial Electronics, 2007. Proceedings of the 2007 IEEE ISIE International Symposium on. IEEE, 2007: 3108-3113.
(编辑:贾志超)
Method of the 2nddifferential angular acceleration observer based on series position linear-fitting differential filters
QIU Wen-bin, CHAI Jian-yun, SUN Xu-dong, LU Hai-feng, FAN Ming
(State Key Lab of Power Systems, Department of Electrical Engineering, Tsinghua University, Beijing 100084,China)
The acceleration feedback can provide higher stiffness of the servo control system, and improve the system robustness. However, acceleration control is seldom implemented in practical, due to the high-frequency noises which are amplified by the 2nddifferential operation of position. Firstly, three kinds of angular acceleration observer based on polynomial curve fitting were thoroughly analyzed, and the results show that the 2nddegree polynomial angular acceleration observer has the best comprehensive performance. Secondly, in order to depress the noise, a method of the series 2nddifferential angular acceleration observer based on the position linear-fitting differential filters was proposed. From the cutoff frequency, white noise magnification and delay time, its performance was analyzed in three aspects and the comparative analysis was carried out between the proposed method and the 2nddegree polynomial observer. Better noise rejection ability of the proposed method is verified by simulations and experiments.
angular acceleration; polynomial curve fitting; angular acceleration observer; series 2nddifferential observer; high-frequency noises
2015-03-17
国家自然科学基金(51277102)
邱文彬(1981—),男,博士研究生,研究方向为运动控制、伺服控制;
柴建云(1961—),男,博士,教授,博士生导师,研究方向为风力发电、电机设计、电机控制;
陆海峰
10.15938/j.emc.2016.01.013
TP 242,TP 216
A
1007-449X(2016)01-0088-06
孙旭东(1965—),男,博士,教授,研究方向为电机设计、电机控制;
陆海峰(1976—),男,博士,副教授,研究方向为电动汽车控制、电机调速;
樊 明(1982—),男,博士研究生,研究方向为电机设计。

