低频往复式微动磨损测试系统驱动频率影响及其实验研究
王仲楠, 王武义, 张广玉
(哈尔滨工业大学 机电工程学院, 黑龙江 哈尔滨 150001)
低频往复式微动磨损测试系统驱动频率影响及其实验研究
王仲楠, 王武义, 张广玉
(哈尔滨工业大学 机电工程学院, 黑龙江 哈尔滨 150001)
为了研究满足现代化设备的连续工作条件以及在微型装置的研制中减小微动磨损的要求,提出一种低成本通用式低频往复式微动磨损测试系统。通过调节驱动电压频率控制运动平台的滑动速度来测试不同摩擦副间的摩擦系数,并分析样本间摆动频率与摩擦系数的关系。开展了硅片、抛光铝、钢、玻璃和聚四氟乙烯与金属钢球构成摩擦副的微动摩擦测量实验。结果表明,当摆动频率小于磨损失效频率时,在较小和较大载荷作用下,摩擦系数随摆动频率增加而近似线性下降;而在载荷较大时,低硬度的摩擦副的摩擦系数是随着频率增加而下降,其摆动频率对摩擦系数的影响与文献中的变化规律相一致,验证了该系统的工作可靠性,且研究结果会对微动磨损的下一步研究提供重要的参考价值。
驱动频率控制; 电磁力驱动装置; 微动磨损; 法向载荷; 摆动频率; 摩擦系数
0 引 言
微动磨损是由两个物体接触面间因出现周期性的微小振幅而造成损伤的一种磨损形式,会导致机构的使用寿命减少、运行精度和操作可靠性降低。工程中的微动磨损常出现在紧配合部位,难以及时发现和观察,导致在一段时间后才出现损伤。现代化微型装置如MEMS/NEMS系统、微型机器人和微型电机等,需要满足越来越高的连续工作特性和自动化程度,以及复杂多变的工况条件,故微动磨损现象已经不容忽视。
有关微动磨损机理,早在1927年Tomlinson就指出,相对运动是产生微动的必要条件,特别是数量级为几个纳米的极小运动也能产生微动损伤。这种滑移幅值较小的微动问题已经成为当前研究的热点,但试验中遇到的一个关键问题是如何控制和测量这种运动的微小幅值。赫兹弹性接触理论是解决球与平面静态接触问题的最佳方法,它证明了接触面上施加切向力会在圆形接触区外产生滑移,如果施加力产生振荡,则在滑移区会出现微动现象。
由于发生在真实表面接触情况下的微动现象非常复杂,故通常采用实验方法来模拟和研究表面间的接触情况。英国学者R.B.Waterhouse教授在《微动磨损与微动疲劳》一书中指出,微动磨损测试实验主要是研究滑移幅值、法向载荷、振动频率及微动状态所处的工况(如接触形式、振动模式及表面状态等)对微动产生的影响。国内外学者通过大量实验也已经证明,实际的两固体界面只在一些较高的微凸体上发生接触,并由这些不连续的微小接触点变成了真实的接触面积,在接触时产生的变形主要取决于名义应力、表面粗糙度和材料常数等因素,受载接触表面的变形可能是弹性变形或塑性变形。理想的两异形固体表面接触时,如果不考虑其受载后发生的弹性变形,则全部载荷可以认为都作用在一点或一条线上。根据这一假设条件得到的实际载荷作用点位移是不真实的,其原因是假设载荷集中作用于一点与实际情况不符合,故忽略接触物体在接触处的几何形状不能用来直接计算工程中的接触问题。为此,根据Tomlinson的“微动滑移”概念和赫兹理论接触模型,本文提出了一种微动磨损测试系统。选择球与平面接触工况,并设计了正弦电磁力驱动的低频往复式运动平台来模拟“微动滑移”。该系统可用于研究现代化设备中金属、非金属以及高分子聚合物等各种材料在滑移区内的微动状态。
1 正弦电磁力驱动频率及装置
本文研制的低频往复式微动磨损测试平台是用于样本表面间在往复滑动状态下的摩擦性能检测设备,配用英国华威大学计量实验室设计的新型微摩擦测量头[1-2],组成为一个通用式低频往复微动磨损测试系统,如图1所示。其中,新型微摩擦测量头是用于提供测量实验中法向载荷的施加和水平摩擦力的测量。
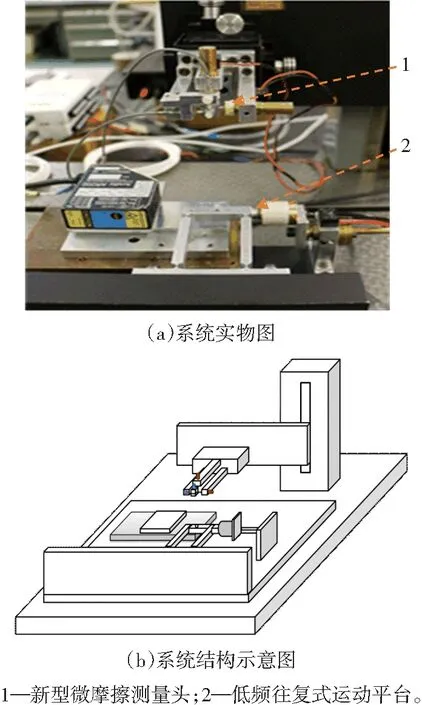
图1 通用式低频往复微动磨损测试系统
低频往复式微动磨损测试平台主要由激光位移传感器、摆动架和电磁力驱动装置组成。摆动架固定在实验台的水平方向上,用于承载测试样本;它的一侧与电磁力驱动装置相连,另一侧为激光位移传感器。电磁力驱动装置是由镶嵌在摆动架一侧的磁铁(Φ=1 cm)和同侧的螺管线圈,功率振荡器以及数字式显示装置组成,通过调节功率振荡器的频率和幅值来驱动电磁力,从而控制摆动架的摆动频率(速度)和滑移幅度。如图2所示为测得的功率振荡器工作频率为1.67 Hz时的摆动架位移曲线s-t,最大摆动幅度0.375 mm(离开平衡位置距离),最大摆动速度为3.925 mm/s。激光位移传感器采用波兰Schmitt公司研发的AR200-6M,用于实时测量和监控摆动架的水平滑移振幅。低频往复式微动磨损测试平台的组成部件的性能参数如表1所示。
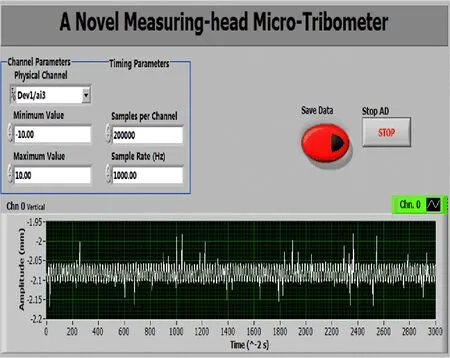
图2 摆动频率为1.67 Hz时摆动架s-t曲线
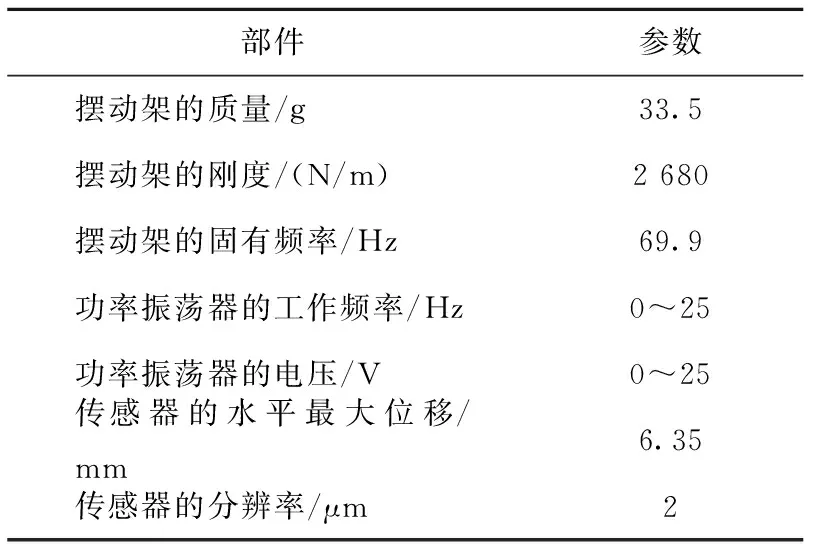
部件参数摆动架的质量/g33.5摆动架的刚度/(N/m)2680摆动架的固有频率/Hz69.9功率振荡器的工作频率/Hz0~25功率振荡器的电压/V0~25传感器的水平最大位移/mm6.35传感器的分辨率/μm2
2 微动摩擦原理及其主要影响参数实验研究
2.1 球-平面多次微凸体接触面积与法向载荷和材料特性的关系
对于球-平面接触区圆形接触面积(见图3[1]),多次微凸体的接触,应用赫兹接触模型简化计算公式得到圆形接触面积为
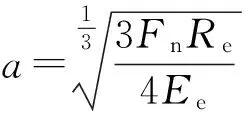
(1)
式中:a为圆形接触面积;Fn为法向载荷;Re是所受压力的球的半径;Ee为弹性模数。Ee通过两接触固体的样式模量Eball、Eflat和他们的泊松比vball、vflat求得

(2)
弯曲变形时的挠度δ为
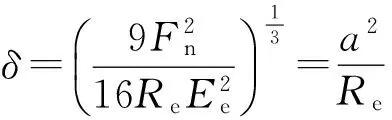
(3)
赫兹接触应力分布p为

(4)


(5)

图3 球-平面接触微动滑移与受力示意图
2.2 滑动摩擦系数的影响因素
滑动摩擦是指相互接触的两个物体,在外力作用下发生的相对滑动运动。1699年,法国科学家G.Amontons受到达芬奇的著名假说启发,通过大量的摩擦实验发现,摩擦力总是等于法向载荷的1/3,而与摩擦材料的表面面积无关[11]。随后,物理学家C.A.Coulumb在1785年进行了更为详细的试验研究后,肯定了Amontons得出的摩擦结论并建立了第四摩擦定律[12]。在古典摩擦定律中,摩擦系数对一定材料来说,是一个常数。然而,经过多年的研究探索,发现许多摩擦结论存在着局限性和不确切性。实际试验表明,各种材料在不同工况下的摩擦系数是变化的。对于硬材料如(钻石)或软材料(如聚四氟乙烯)等,当压力很大时,摩擦力并不与法向载荷成正比。例如,国内外许多著名学者研究了滑动速度对摩擦系数产生的影响。在不同的实验条件下得出的结果很不一致。法国人B.Bochet通过机车车辆的制动试验,得出了摩擦系数随滑动速度变化的表达式[11]为
μ=K/(1+0.23v)。
(6)
式中:K为对不同材料的系数,例如对干煤钢轨为0.45,对潮湿钢轨为0.25;v为滑动速度m/s。而德国学者G.Franke提出的摩擦系数与速度的关系式[12]为
μ=μ0e-cv。
(7)
式中:μ0为静摩擦系数,c为常数。前苏联专家克拉盖尔斯基,曾根据选定速度范围和压力变化范围做了相关的摩擦系数测试实验,得到了摩擦系数与滑动速度的关系[13]为
μ=(a+bv)e-cv+d。
(8)
式中a、b、c、d是与摩擦材料及载荷大小有关的常数。
由式(8)得到图4[13]表示的不同载荷下滑动速度与摩擦系数的关系曲线。在中等载荷时,当速度v较小,摩擦系数会随着滑动速度的变化而达到一个最大值,负载越大和表面越硬的物体,摩擦系数的最大值就会越靠近坐标原点。然而,在更高的速度下,强烈的摩擦热会改变材料表面接触层的状态,可能会使表层大面积呈熔化状态,导致摩擦系数随着滑动速度v的进一步增大而显著降低。
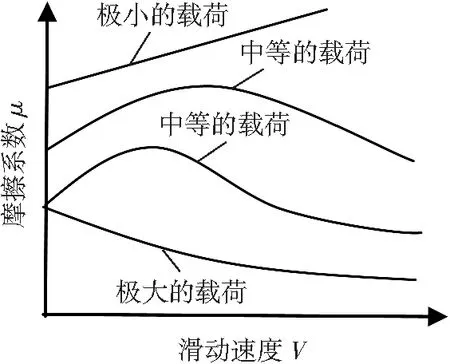
图4 不同载荷下滑动速度与摩擦系数的关系曲线
3 低载荷下变驱动电压频率的摩擦系数测试
测试实验的目的在于通过调节驱动电压频率来获得不同材料在设定载荷下的摩擦系数,进而分析电磁力驱动装置和往复平台之间有效的频率控制范围。
经对系统进行标定,得到测量头的载荷范围为0~60 mN,实验中选取3个设定值(9.65、46.68、58.83 mN)来分别进行微动摩擦测试。尺寸为10×10×1 mm3的硅片、钢、玻璃、抛光铝和聚四氟乙烯5种不同材料,与直径为1 mm的小钢球构成不同的摩擦副。电磁线圈驱动频率的范围在1.5~10 Hz之间,在实验中设定的驱动频率为1.67 Hz,5 Hz和8 Hz。测试是在温度为22 ℃和相对湿度为43%的密闭实验室中进行的。根据图4的关系曲线可以看出:
1)小载荷下,无论何种摩擦副,摆动频率越高摩擦系数越小,特别是钢和抛光铝样件的摩擦系数近似指数下降,与文献[13]中摩擦系数与速度的关系式(2)相符。但是,在图5中,对于金属-非金属摩擦副,在5 Hz后摩擦系数存在最小值,即摆动频率-摩擦系数的变化曲线出现明显的拐点频率(5 Hz),然后摩擦系数值随着频率的增加反而变大,这说明当滑动速度很大时,由于释放出很多热量而使金属-非金属摩擦副(非金属材料较软)的摩擦表面发生了显著变化,以至于摩擦系数会随着滑动速度的增加而变大。该拐点应为载荷的极限点,而极限点就是磨损失效点。摆动频率的增加意味着滑动速度的增加,因此在小载荷下,在磨损失效点前,摩擦系数会随着滑动速度增加而下降,这与图4中曲线“1”载荷下的情况恰恰相反。因此,如果在应用中能够有效地控制加载摆动频率,也就控制了滑动速度和摩擦系数。

图5 载荷9.65 mN下摆动频率-摩擦系数曲线
2)中等载荷下,对于硬度高的摩擦副,其摆动频率-摩擦系数的变化曲线有最大值,而硬度低的摩擦副的摆动频率-摩擦系数曲线有最小值。同样,在磨损失效点5Hz附近出现拐点。由图6可知,不同材料的摩擦副,在中等载荷的条件下,随着摆动频率的增加,摆动频率-摩擦系数曲线会出现不同的变化趋势。具体来说,抛光铝、硅片和钢的摆动频率-摩擦系数曲线均呈现出抛物线形状,会随着摆动频率的增加而达到一个最高点,随后开始下降,在8Hz时会降到相近的范围内。玻璃的摩擦系数曲线表现为下降趋势,并从5 Hz时开始,基本稳定在摩擦系数值大约为0.006的位置上。而PTFE的摩擦系数曲线只有上升部分,不过这仍然与文献[13]中的结论相一致,也就是说这种高分子材料的表面发生变化导致其摩擦系数随着滑动速度的增加而依然呈现上升趋势。根据前苏联专家克拉盖尔斯基[13]的实验结果,在不同载荷下,摩擦系数随着滑动速度的增大都要通过一个最大值。因此,在中等载荷下条件下,硬度高的摩擦副的摆动频率与摩擦系数的曲线依然能够呈现出与图4较相似的变化规律。
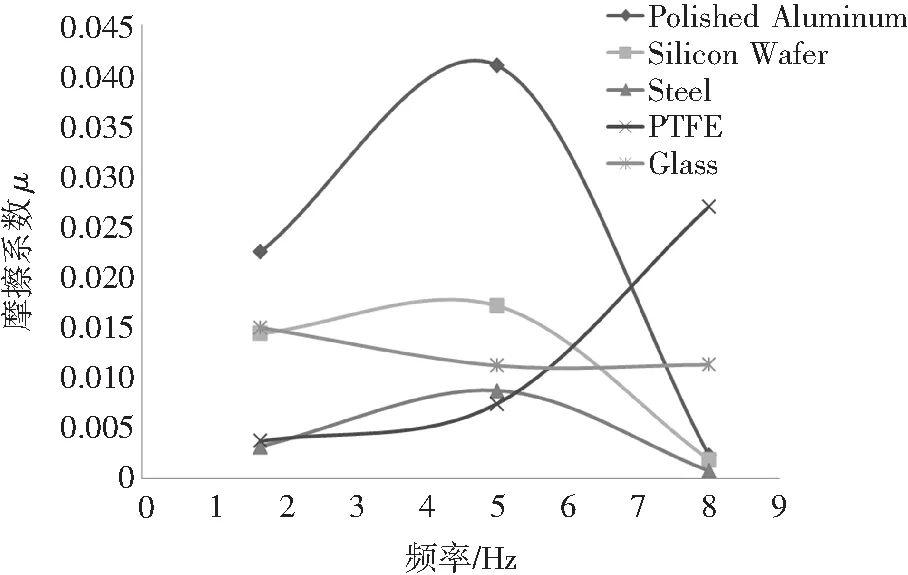
图6 载荷46.68 mN下摆动频率-摩擦系数曲线
3)较大载荷下,摆动频率-摩擦系数曲线近似线性下降。由图7可以看出,在载荷58.83mN作用下,除聚四氟乙烯外,其余4种不同样件(硅片、钢、抛光铝和玻璃)在最小摆动频率1.67Hz(即最小滑动速度)时测得的摩擦系数值为最大,随着载荷和速度的变化而呈现出上升曲线、抛物线状或者(指数)下降趋势。然后,它们的摩擦系数值会随着摆动频率的不断增加近似线性地减小,这与图4中曲线“4”的结果较吻合。不过,PTFE的摩擦系数曲线依然只呈现上升趋势,这与在较小载荷和中等载荷时的变化是一致的。因此,无论法向载荷的大小如何,球-PTFE摩擦副间滑动摩擦系数曲线变化类似,摆动频率-摩擦系数曲线有最小值,在磨损失效点5Hz附近出现拐点。
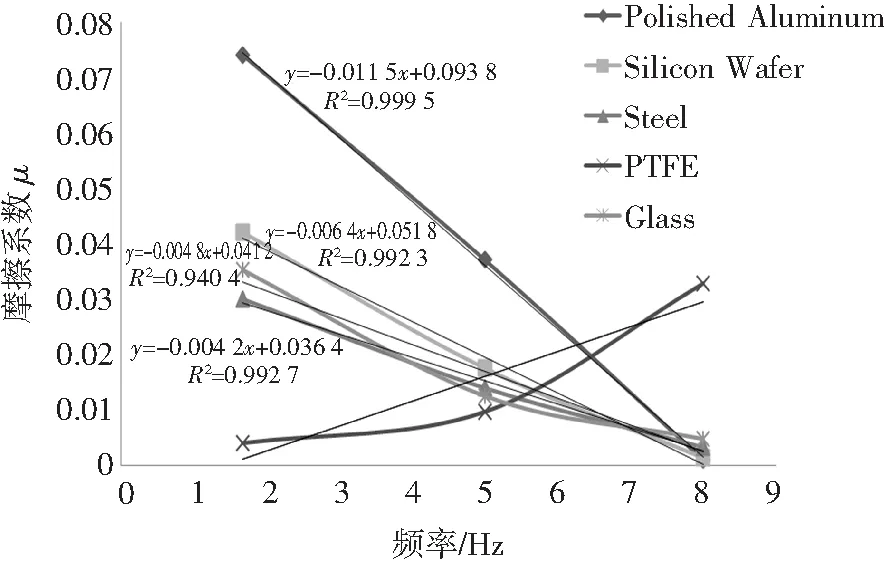
图7 载荷58.83 mN下摆动频率-摩擦系数曲线
4 结 论
本文设计并研制了电磁力驱动装置,通过调节驱动信号频率来控制低频往复式摆动平台的滑动速度。任选了5种金属和非金属样本与小钢球构成不同的摩擦副,在变电磁力信号频率和变载荷的条件下进行了多次摩擦测试实验,得到了样本摆动频率与摩擦系数的关系曲线。当摆动频率小于磨损失效频率时,在较小和较大载荷作用下,摩擦系数随摆动频率增加而近似线性下降;在载荷较大时,低硬度的摩擦副的摩擦系数随着频率增加而下降,而硬度高的摩擦副的摩擦系数却有相反的结果。由此说明,在设定的测试环境中(温度和湿度)中,低频往复式微动磨损测试系统驱动电压频率可以有效地控制微动磨损测试中的滑动速度。本文的研究结果对今后在微动磨损研究领域提供参考。
[1] DEREK G Chetwynd, MOHAMMAD S Alsoufi. A novel micro-friction measuring-head using force-feedback compensation [C]//Proc. SPIE V7544. Sixth International Symposium on Precision Engineering Measurements and Instrumentation, 2010, Hangzhou, China. 2010: 754417.
[2] PAROS J M,WEISBORD L. How to design flexure hinges[J]. Machine Design, 1965, 37: 151-156.
[3] 蔡振兵. 扭动微动损失机理研究[D]. 成都: 西南交通大学, 2009.
[4] TREASE B P, MOON Y M, KOTA S. Design of large-displacement complaint joints[J]. Journal of Mechanical Design, Transactions of the ASME, 2005, 127: 788-798.
[5] 刘立平. 往复式摩擦磨损试验机的研制[D]. 甘肃:兰州理工大学, 2006.
[6] 杨婕斐. 微动摩擦测试仪的研究设计[D]. 北京: 北京邮电大学, 2008.
[7] MENG Y G, JIANG H J, WONG P L. An experimental study on voltage-controlled friction of alumina/brass couples in zinc stearate/water suspension[J]. Tribology Transactiom, 2001, 44(4): 567-574.
[8] ZHOU Z, VINCENT L.Fretting wear[M].Beijing:Science Press,2002.
[9] 温诗铸, 黄平. 摩擦学原理[M]. 北京: 清华大学出版社, 2008: 5-8.
[10] ZHU M H, ZHOU Z R. An experimental study on radial fretting behavior[J]. Tribology International, 2001, 34: 321-325.
[11] 王国强, 马若丁, 刘巨元, 等. 金属摩阻材料间摩擦系数与滑动速度关系的研究[J]. 农业工程学报,1997,13(1): 35-38.WANG Guoqiang, MA Ruoding, LIU Juyuan, et al. Study on the coefficient of dynamic friction between frictional metal material[J]. Tarnsactions of the CSAE, 1997, 13(1): 35-38.
[12] 董云开, 刘莹, 张向军, 等. 环境湿度下硅材料表面的粘滑行为及其抑制[J]. 润滑与密封,2007, 32(4): 1-5.DONG Yunkai, LIU Ying, ZHANG Xiangjun, et al. Control of stick-slip phenomenon on silicon interface under relative humidity conditions[J]. Lubrication Engineering, 2007, 32(4): 1-5.[13] 〔苏〕克拉盖尔斯基. 摩擦磨损计算原理[M]. 北京: 机械工业出版社, 1982: 194-195.
[14] MIGANNAD S Alsoufi. A high dynamic response micro-tribometer measuring-head[D]. Coventry: University of Warwick, 2011.
(编辑:刘琳琳)
Experimental research on driving frequency influence of low-frequency reciprocating fretting wear testing system
WANG Zhong-nan, WANG Wu-yi, ZHANG Guang-yu
(School of Mechatronics Engineering, Harbin Institute of Technology, Harbin 150001, China)
In order to meet the requirements of continuous operation to modernized equipments and reduction of fretting wear for micro-device manufacture, a low-cost universal low-frequency reciprocating fretting wear test system was developed. Oscillation reciprocating of reciprocating platform was controlled by adjusting the frequency of driving voltage to measure the coefficient of friction (CoF) for different friction pair, and analysis the variation of CoF with oscillation frequency. The micro-friction measurement were carried on with silicon wafer, polished aluminum, steel, glass and polytetrafluoroethylene (PTFE) against a steel ball. The experiments showed that CoF decreases linearly with the increase of oscillation frequency at the lower and higher applied load before the wear failure frequency occurred. Moreover, the friction coefficient for friction pair with the lower hardness shows a similar decline curve and variation of friction coefficient with oscillation frequency is consistent with the published literature. It is concluded that the test system is available and results will be provided as an important reference for future research in the field of fretting wear.
driving frequency control; magnet-coil force actuator; fretting wear; normal load; reciprocating frequency; coefficient of friction
2014-11-03
王仲楠(1984—),男,博士研究生,研究方向为微系统测试与摩擦特性研究;
王武义(1957—),男,教授,博士生导师,研究方向为微系统测试与摩擦特性研究、超声波技术;
王仲楠
10.15938/j.emc.2016.01.016
TH 117.1
A
1007-449X(2016)01-0105-05
张广玉(1962—),男,教授,博士生导师,研究方向为微系统测试与摩擦特性研究、机电一体化技术。

