基于广义系统观测器的电池荷电状态估计

何朕， 王广雄

(哈尔滨工业大学 航天学院，黑龙江 哈尔滨 150001)



基于广义系统观测器的电池荷电状态估计

何朕， 王广雄

(哈尔滨工业大学 航天学院，黑龙江 哈尔滨 150001)

提出了一种新的电池荷电状态(SOC)的估计方法。电池的开路电压(OCV)与SOC之间是一种分段线性的关系，为了避开这类非线性问题，观测器设计时的通行做法是将输出电压的方程式对时间进行求导。文中分析表明这种对电压方程求导的做法是不正确的。指出可以将分段线性关系看做是广义系统中的一种线性约束，从而提出用广义系统观点来处理电池的这个分段线性约束，并且设计了广义系统观测器。仿真结果表明所提出的观测器的有效性。

广义系统; 观测器; 电池; 荷电状态

0 引 言

使用汽油的汽车其剩余油量是很容易测得的。如果是电动汽车，电池的剩余容量则是从荷电状态(state of charge,，SOC)信息得到的。SOC是电池内部的化学状态，无法用电的信号来测量，所以要通过电池端口的电压，电流等物理量的测量进行估计。如果是纯电动车，则主要是放电问题，SOC的估计问题相对简单一些，不过如果是混合电动车，则电池存在重复充放电过程，如果估计不准，有可能使估计误差累积起来，造成电池过充或可能全部耗尽，造成不可逆的损坏，所以SOC的精确估计对驾驶员和电池的能量管理系统来说都是极为重要的。

电池有多种模型，不过从估计的角度来说，一般都是采用电池的电路模型。电路模型中常用电压源来表示电池。电压源所表示的是开路电压(open-circuit voltage，OCV)，开路电压voc与电池的荷电状态SOC直接有关，是一种近似分段线性的关系，所以一般都是从voc来估计SOC。

文献[1]中是用一个很大电容上的电压来代表voc的，不过现在大多数的工作都是用电压源来表示voc的。早期的工作[2]是将voc当作电路中的一个参数与其他参数合在一起来进行估计的。Plett根据电流与荷电量之间的积分关系提出了一个SOC的状态方程[3]。Plett用多个参数来逼近voc与SOC的非线性特性并采用扩展Kalman滤波来估计SOC状态，但Plett只采用仅有一个状态(即SOC)的电路，也就是电池加内阻的内阻模型[2]。由于没有考虑到电容，故内阻模型不是一种动态的模型[2]。Kim基于积分关系的SOC的状态方程，按分段线性化的概念来处理一般的包含有电容的电路模型，并采用滑模观测器来估计SOC状态[4]。Kim的主要思路是一个分段线性化的方程可以按线性的概念来对时间求导。这个处理SOC非线性方程的做法方便了观测器的设计，所以得到了一系列文章的响应，例如文献[5-6]。分段线性系统采用求导的做法对某一工作点的分析是可以的，但是用在全行程的估计却是存在问题的。另外，基于Kalman滤波的一些方法理论上也是可以用来估计电池SOC的，不过本文的重点是要说明当前采用观测器设计时的求导做法存在一个概念上的问题，故本文采用观测器来进行估计。本文将分析用求导方法的SOC状态估计所存在的问题，并提出用广义系统的状态观测器来估计SOC。

1 电池的建模

电池的RC电路模型有数种类型，不过都大同小异。由于本文的对比对象是文献[4]，所以采用文献[4]的电路模型(图1)作为研究对象。该电路模型由电压源voc(z)和相应的电阻电容构成。非线性电压源voc(z)是一个用开路电压来表示的与电池SOC有关的电压。这里z代表SOC。Cp是代表极化效应的电容，vt是可以观察的终端电压，I为充放电电流。Rb为传导电阻，Rp为扩散电阻，Rt为端电阻，Ib和Ip为两支路电流。

SOC定义为电池剩余容量与额定容量的比值。设充放电起始状态为SOC0，那么当前的状态SOC为

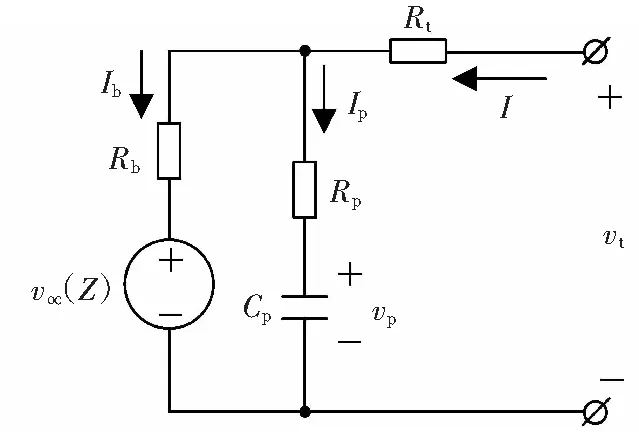
图1 电池模型

(1)

式中CN为电池的额定容量，公式中的电流放电为正，充电为负。ηi为电池的库伦效率(Coulombic efficiency)，放电时ηi=1，充电时ηi1。

设用变量z(t)来表示电池的SOC，Plett将式(1)改写成[3]

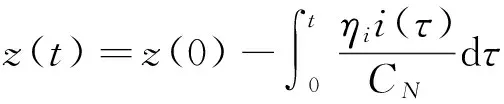
(2)

根据式(2)可写得SOC的z的微分方程为

(3)

根据图1的电流方向，故式(3)的右项取(+)号，又下面的算例中主要针对放电情况，故ηi取为1。

根据图1可写得端电压vt的电压方程为

vt=IRt+IpRp+vp，

(4)

vt=IRt+IbRb+voc(z)。

(5)

从式(4)、式(5)可写得

IpRp=IbRb+voc(z)-vp。

(6)

又从式(3)可得

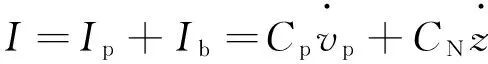
(7)

从式(6)、式(7)得

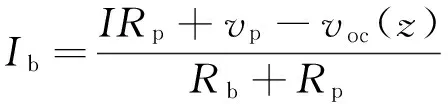
(8)

将式(8)代入式(3)，得

(9)

类似的推导，从式(7)、式(8)、式(9)可得

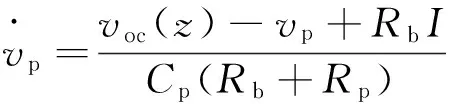
(10)

从式(5)和(8)可得

(11)

除了上面这三个方程式外，还有一个开路电压voc与SOC的非线性关系voc(z)。这个关系可近似为一个线性关系[3-5]，更确切说是一个分段线性的关系。

voc(z)=k1z+k2。

(12)

式(12)也可用图表示如图2所示。

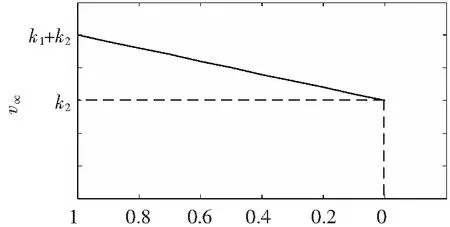
图2 voc与z的关系图

式(9) ～ (12)就是电池的数学模型，文献[4]给出的模型中各参数为：电池的额定容量

CN=5.0 Ah=5×3 600=18 000 A·sec，

Cp=200 F，Rt=0.001 Ω，Rb=Rp=0.003 Ω，

k1=1.2，k2=3。

将这些参数代入后，系统的方程式为

2 现有观测器设计中的问题

有了数学模型，现在的任务是要设计观测器来给出SOC的状态估计。电池数学模型中有两个状态变量，z和vp，但是SOC的状态z是内部变量，与voc存在一个分段线性的关系式。为了解决这个分段线性的非线性系统的设计问题，Kim提出了一个对时间求导数的办法[4]，因为分段线性特性求导后，导数之间存在着线性关系。

具体做法是对式(12)求导，并将式(9)代入，得

(14)

文献[4]再对vt的式(11)求导，并认为电流I的变化率很小而给予忽略(注：这一点实属勉强)，得

将式(10)、式(14)代入上式，再根据式(11)进行整理，得

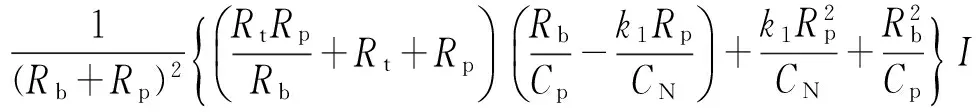
(15)

这里要说明的是，这些公式与文献[4]中的式子略有不同，故一并列出以供参考。

将各具体参数代入式(14)式(15)后，得系统的方程式为

(16)

(17)

式中

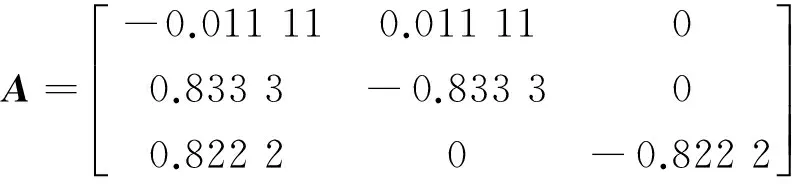
这样，用求导数的办法得到了一组系统的线性方程，观测器的设计问题也就迎刃而解了。文献[4]在考虑了其他非线性不确定因素后决定采用滑模观测器的设计问题。本文则认为这个基本的系统方程式(17)本身就存在着问题，所以下面采用常规的观测器来进行讨论。

根据式(17)，取观测器方程为

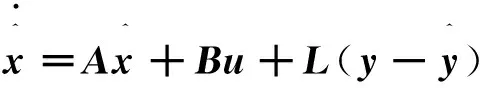
(18)

这个观测器是很容易设计的，设求得的观测器增益为

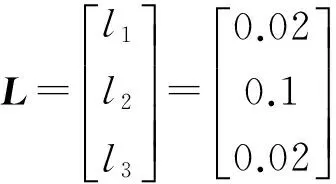
(19)

下面来对观测器进行仿真。图3就是进行仿真研究的框图，图中虚线以上部分就是带有非线性特性的真实系统的数学模型[式(13)]，是个二阶系统。虚线以下部分则是按求导方式推导得出的观测器方程式(18)。由于人为的求导运算，使这个观测器成为一个三阶系统。上下两部分的阶次都不相同，可见用求导观点设计的观测器与实际系统并不匹配，所以从理论上来说，观测器的误差是否收敛都是成问题的，可是文献[4]并没有意识到这个问题。

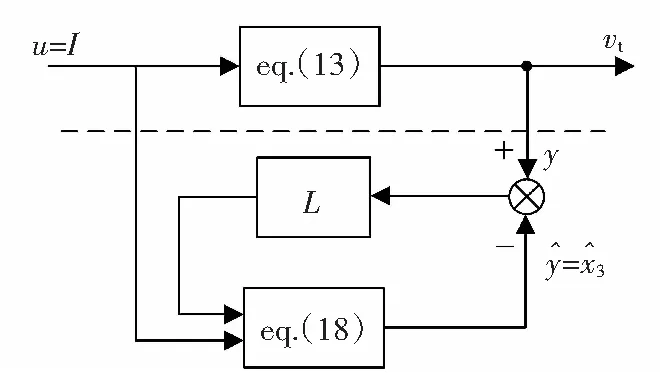
图3 系统与观测器的仿真框图

现在来进一步分析具体的仿真效果。这里采用文献[4]中的实验条件，即用一串恒值电流来放电，放电电流5A，放电180秒，然后停止放电静止3 600秒，即每次减少5%的SOC的量。电池开始时是满充到4.2V，图4是前几个脉冲放电下的仿真结果，图中给出了电池端电压、电压的估计值和估计误差。图中还列出了SOC的真实值(图3上半部系统的z(t))，SOC的估计值和估计误差。

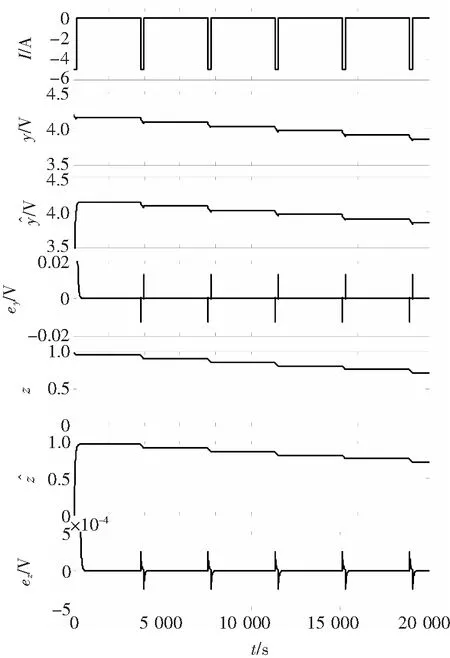
图4 观测器式(18)的仿真结果

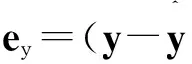
3 广义系统观测器的设计

文献[4]之所以采用求导方法来设计观测器，是为了克服分段线性系统在观测器设计上的困难。其实分段线性可以看做是变量之间的一种代数约束，所以这里的问题完全可以用广义系统的概念来处理。具体来说，式(13)就是一个广义系统的方程组。该广义系统有三个变量：z和vp是两个状态变量，voc是一个代数变量，最后一个是输出方程。

(20)

y=0.5x2+0.5x3+0.002 5I。

(21)

或可写成矩阵形式为

(22)

y=Cx+Du。

(23)

式中

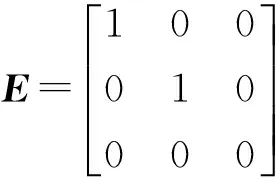
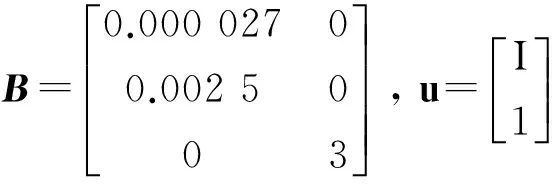
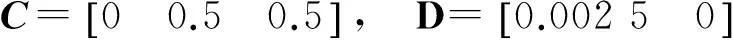
由此可见，电池SOC的估计问题实质上是一个广义系统的观测器设计问题。而与式(22)式(23)对应的这类广义系统观测器的一般形式为[7]

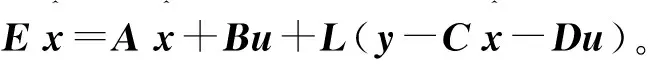
(24)

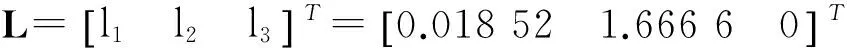
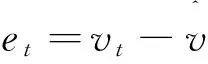
图5 广义系统观测器的仿真结果

4 结 论

电池荷电状态的估计是一个分段线性系统的估计问题。为了避开分段线性问题，当前通行的做法是加一求导过程。本文分析指出这种求导后得出的观测器，在理论上并无充分依据，而且还有估计误差，进而提出用广义系统观测器来估计SOC。本方法简单实用，且能保证估计的精度。

当然SOC的估计问题中有时还会加进一些对电路模型中其他参数的估计，例如[2, 8]。但是估计问题中对系统模型的认识是首要的，只要认识到这是一个广义系统问题，剩下的就只是具体的设计方法了。这也是本文想传达的一个思想。

[1] JOHNSON V H. Battery performance models in ADVISOR[J]. Journal of Power Sources, 2002, 110(2): 321-329.

[2] PANG S, FARRELL J, DU J, et al. Battery state-of-charge estimation[C]//Proceedings of the American Control Conference, Arlington, VA. June 25-27, 2001: 1644-1649.

[3] PLETT G L. Extended kalman filtering for battery management systems of LiPB-based HEV battery packs. Part 2. Modeling and identification[J]. Journal of Power Sources, 2004, 134(2): 262-276.

[4] Kim I S, Nonlinear state of charge estimator for hybrid electric vehicle battery[J]. IEEE Transactinos on Power Electronics, 2008, 23(4): 2027-2034.

[5] Chen W, Chen W T, Saif M, et al. Simultaneous fault isolation and estimation of Lithium-Ion batteries via synthesized design of Luenberger and Learning observers[J]. IEEE Trans actions on. Control Systems Technology, 2014, 22(1): 290-298.

[6] 张云, 张承慧, 崔纳新. 锂离子电池荷电状态估计: 非线性观测器方法[J]. 控制理论与应用, 2012, 29(12): 1639-1644.

ZHANG Yun, ZHANG Chenghui, CUI Naxin. Estimation of state-of-charge of lithium-ion battery: nonlinear observer method [J]. Control Theory and Applications, 2012, 29(12): 1639 - 1644.

[7] HOU M, MÜLLER P C. Design of a class of Luenberger observers for descriptor systems. IEEE Trans. Automatic Control, 1995, 40(1): 133-136.

[8] 于智龙, 郭艳玲, 王海英. 自放电修正的锂动力电池SCKF-STF的SOC估算策略[J]. 电机与控制学报, 2013, 17(10): 70-76.

YU Zhilong, GUO Yanling, WANG Haiying. Research on state-of-charge estimation of Li-ion battery based on SCKF-STF [J]. Electric Machines and Control, 2013, 17(10): 70-76.

(编辑：刘素菊)

Descriptor system observer-based state-of-charge estimation for batteries

HE Zhen, WANG Guang-xiong

(School of Astronautics, Harbin Institute of Technology, Harbin 150001, China)

A new method for battery state-of-charge (SOC) estimation was proposed. To avoid the difficulties in treating the piecewise linear relationship between the open-circuit voltage (OCV) of the battery and the SOC, the popular approach for the observer design is to take the time derivative of the equation of the output voltage. It shows that the design of the observer by taking the time derivative of the voltage equation is incorrect. It is pointed out that the piecewise linear relationship can be considered as a linear constraint of a descriptor system. So the descriptor system approach was proposed to cope with this piecewise linear constraint. And the descriptor system observer was then designed. Simulation shows the effectiveness of the proposed method.

descriptor system; observer; battery; state of charge

2015-06-10

国家自然科学基金(61174203,60374027);国家自然科学基金重点项目(61034001)

何 朕(1972—)，女，博士，教授，研究方向为控制系统设计、鲁棒控制及H∞控制等；

王广雄(1933—)，男，教授，研究方向为控制系统设计、鲁棒控制及H∞控制等。

何 朕

10.15938/j.emc.2016.01.014

TP 273

A

1007-449X(2016)01-0094-05