基于遗传算法KMV模型的最优违约点确定

冯 敬 海， 田 婧

( 大连理工大学 数学科学学院, 辽宁 大连 116024 )



基于遗传算法KMV模型的最优违约点确定

冯 敬 海*， 田 婧

( 大连理工大学 数学科学学院, 辽宁 大连 116024 )

现代市场经济中资信评估具有重要作用，它起着社会监督和识别违约风险的作用．根据可获得的中国上市公司的基本数据，结合遗传算法对经典KMV模型中的最优违约点进行了重新定义．结果显示改进的模型拟合正确率比原模型高，即改进的KMV模型更适合应用于中国上市公司的资信状况评估．

期权定价；KMV；遗传算法；信用风险

0 引 言

2011年以来的欧债危机使得我国许多企业受到了猛烈的冲击．上市公司是我国国民经济的中流砥柱，同时又是商业银行的主要贷款客户，其信用风险问题备受关注．加之不景气甚至有些低迷的经济环境下，很多上市公司的业绩出现了下滑，进而导致了信用风险的上升．

对于普通的经营者来说，如果其具有较高的信用等级，就可以降低交易的成本，提高效率以及核心竞争力；但是，如果公司的信用等级比较低，融资难度就有可能增加，进而导致流动性资金短缺、生产困难、财务周转危机，甚至破产．由于其破产往往带有连带效应，与其有关联的公司、银行等也会因此遭受损失，进而导致金融市场的失灵．

在这样的情况下，如何根据中国的实际国情，建立一套可以准确预测和识别上市公司风险的理论体系和体制，进而保证经济的合理稳定健康运行，是现今我国学者面临的一个重要难题．

本文选取KMV模型度量上市公司信用风险．KMV模型[1]是美国旧金山市KMV公司于1997年推出的评估信用风险的违约预测模型．截至目前，KMV模型主要包括两方面的内容：一部分[2-4]是关于信用风险度量的指标，包括信用检测、非公开上市公司模型及EDF计算工具；另一部分[5-6]是关于投资组合管理、全球化风险与报酬相关系数计算工具．

目前国内对KMV模型的研究动态分为两类：

一些研究者直接使用KMV模型对我国上市公司的违约风险进行评估，验证其有效性，研究结果大多表明： KMV模型比较有效，它可以在违约事件发生或破产前有效地预测到资信状况的变化；它适用于任何股权公开交易的公司．

还有一些研究者应用修正后的KMV模型评估我国上市公司的违约风险，检验其有效性．KMV模型中有些参数之间的关系作为公司的内部机密并没有公开，我国的研究者主要对这方面进行了探索，并且参数之间的关系是依据我国的实际国情给出的，具有应用价值；另外，在KMV模型中，股权价值等于流通股市场价值，暗含上市公司的股权全部流通的假设，虽然我国资本市场自2005年来实行了股权分置改革，但对于非流通股的真正解禁还有一个过渡期限，仍有很多公司存在非流通股，因此部分学者对非流通股定价的问题进行了探讨．

1 预备知识

1.1 KMV模型

KMV模型的原理[7-8]是把公司的负债当作一份看跌期权，而把公司的股权价值当作一份看涨期权，它们的标的物均为公司资产的市场价值．假设资产价值比负债价值小时，公司将发生违约，但KMV公司经过统计分析发现，只有在上市公司资产价值小于某一临界值时，公司才会违约，这一临界值就被称为违约点(DPT)．

KMV模型中的违约距离(DD)表示公司资产价值到违约点的距离，KMV公司利用大量的历史违约数据记录进行统计分析，找出违约距离与预期违约率之间的关系，并将其拟合为一条光滑的曲线，这样便可以找出任何一点上违约距离对应的预期违约率，从而可以对预期违约率的值进行估计．KMV模型的理论框架如图1所示．

模型假设公司的资产价值在风险中性概率测度下服从几何布朗运动：

dVa=rVadt+σaVadz

(1)

式中：Va是公司的总资产价值，r是无风险利率，σa是资产价值收益的波动率，dz是标准的维纳过程．

如果在T时刻公司的负债价值是D，那么现在的公司股权价值和资产价值有如下关系：

Ve=VaN(d1)-De-rTN(d2)

(2)

其中Ve是公司股权价值，N(·)是正态累计分布函数，

由伊藤引理可以得知：

(3)

其中σe是公司股权价值的波动率．

对于上市公司来说，它的股票价格可以比较容易得到，所以公司股权价值及其波动率可以通过股票价格计算得出；资产价值及其收益波动性都是市场上不能直接观察得出的变量，需要联合上述两式才能求出．

KMV模型的最终输出结果是预期违约率EDF，主要通过3个步骤来确定．

步骤1 由股权价值及其波动率估算资产价值Va及其波动率σa，联合式(2)和(3)得出．

步骤2 测算违约距离及违约点．KMV实证研究发现，公司违约频繁发生于公司资产价值在短期负债和长期负债的一半之和这一临界点附近，因此KMV将此点设置为违约点．违约距离是指在一定时期内公司资产价值到违约点之间的相对距离，是一个量纲一的量，能够用于不同资产规模的公司之间进行比较，可以表示为

(4)

测算出来的违约距离可以识别出公司在未来一段时期内的信用风险走势，违约距离和违约可能性成反比，上市公司在交易日的股票价格会不断更新，并定期公布财务指标，因此能够及时地测算违约距离，度量信用风险的变化．

步骤3 求解预期违约率EDF．

EDF有两种算法．一是KMV公司根据大量历史违约数据统计得到的违约率；一是根据下式给出的理论预期违约率：

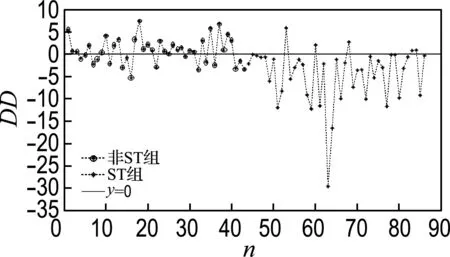
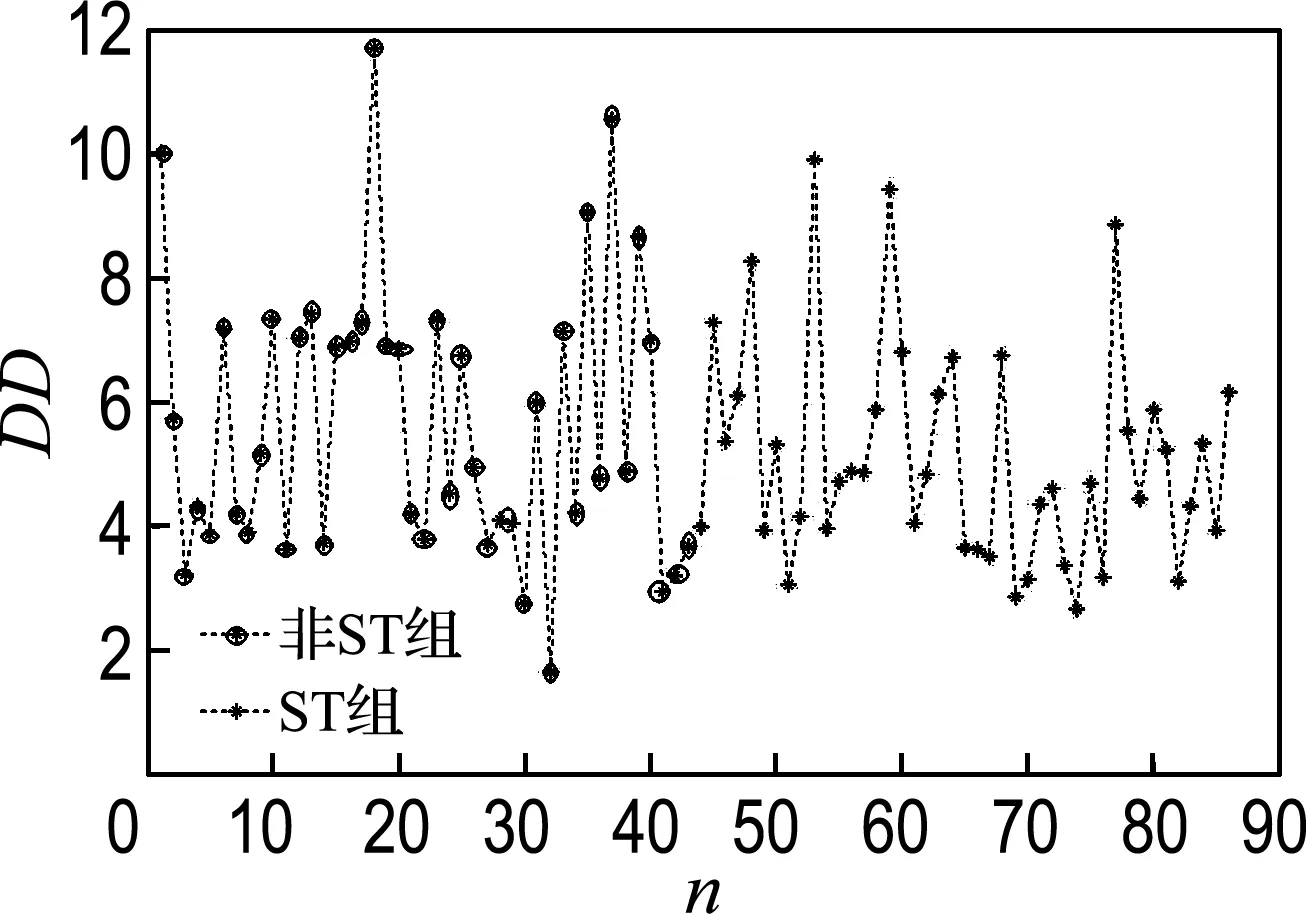
EDF=P(E(Va)

(5)

KMV模型所建立的违约距离与违约率之间的对应关系是根据美国历史上大量的违约数据统计分析后得出的结果，因此经验违约率不可取；同时假定资产价值波动服从正态分布与实际情况并不完全相符，因此利用理论违约率得到的值与现实情况也存在一定的偏差．怎样把违约距离转化为违约率有待研究，因此本文直接用违约距离来度量公司是否违约．

1.2 遗传算法

遗传算法(genetic algorithm，GA)[9]是模仿自然界中生物进化机制和遗传机制而提出的随机优化搜索算法，它是由Holland等首先提出的，是一种非常有效的全局优化算法，非常适合于处理那些传统优化搜索技术不易解决或是不能解决的复杂优化问题．遗传算法通过生成初始种群来进行第一步运行，初始种群通常表示为字符串，即二进制编码符号，然后通过不断地生成下一代根据某种规则来求解问题的最优解．适应度高的个体通过将自身的部分字符串与其他个体的部分字符串进行交换得到下一代个体．在遗传过程中个体的字符串也会发生变异．随着时间的推移，将适应度差的个体进行淘汰，然后利用适应度高的个体在随机选取的相同的字符串点位进行交换得到新的个体，从而产生下一代种群，这种运行方法非常有效．

遗传算法有以下几个构成要素：染色体编码方法、个体适应度评价、遗传算子、运行参数．其中最重要的是确定个体适应度评价函数．

本文以遗传算法为工具来对KMV模型进行改进，进而预测上市公司的信用风险．

2 模拟及结果分析

虽然违约点是KMV模型的重要组成部分，但是针对其的探讨却不多．因为KMV模型中的参数设定是依据KMV公司记录的大量历史违约数据进行统计分析得出的，由此设置的违约点只对美国的上市公司适用，对我国公司不一定适用，所以有必要研究适合于我国国情的违约点的计算公式．

在此，重新定义违约点为DPT(GA)=α×LTD+β×STD．选取上市公司作为样本，将问题化为用遗传算法解决的运筹领域的问题．图2为用遗传算法求解KMV模型最优违约点的流程图．

图2 遗传算法流程图

样本选择分为开发样本和检验样本选择两类．

开发样本的选择：选择2009～2011年3年间我国上市公司中的78家被ST的上市公司作为开发样本计算违约点的最优系数α、β．

检验样本的选择：选择2012～2013年我国上市公司中43家被ST的公司和与之相对应的43家未被ST(非ST)的上市公司作为检验样本，对模型的有效性进行统计分析．

用于KMV模型计算的样本数据均来源于新浪财经数据库和国信证券交易软件．

应用遗传算法对开发样本进行反复迭代，最终得出的最优违约点计算公式关于流动负债和长期负债的最优系数，这样，得出了短期负债(STD)和长期负债(LTD)的最优系数分别为4.302、1.736，而此时开发样本中得出的适应度函数值即模拟的违约正确率结果为1-22.571 4%=77.428 6%，因此最优违约点的计算公式为DPT=4.302×STD+1.736×LTD．将其代入KMV模型中检验对我国上市公司的适应性．

用检验样本检验拟合优良性：检验样本为2012～2013年的上市公司，共86家，其中被ST组与未被ST(非ST)组一一配对；应用上述违约点对检验样本模拟违约结果总正确率达到75.581%，其中违约正确率为38/43=88.372%，不违约正确率为27/43=62.791%．

如图3所示，虽然正常组正确率略低，不过这是可以接受的，从风险控制的角度来看，可以令企业及时采取措施和方法进行自我管理，提高企业的信用等级，保证企业的正常运营．若套用美国经验违约点公式DPT=STD+0.5×LTD计算，检验样本中总正确率为50%,虽然这个数值不低，但是深入研究会发现，该公式把违约公司全部判定为不违约，即完全不能识别公司的违约风险，如图4所示，违约正确率为0．这说明用遗传算法算出的最优违约点要比原模型公式效果好．

图3 最优违约点算出的违约距离

图4 原公式得到的违约距离

3 结 语

本文仅讨论了一种适应我国现有国情的建立新的违约点的方法，且只有样本越大，结论才越准确．而且，西方发达国家的法律法规比较健全，对于企业而言，很少会出现恶意欠款不还的情况，而这在我国确实时有发生，在建模时需要考虑进去．

尽管KMV模型有诸多优点，但是也有其不足的地方：假设条件很严格，实际中上市公司资产收益的分布通常不满足正态分布而是存在“肥尾”现象；对非上市公司由于可使用资料的可获得性差，预测的准确性也较差；没有考虑信心不对称情况下的道德风险等．今后要对此进行深入研究．

[1] Crosbie P, Bohn J. Modeling Default Risk [M]. Sanfrancisco:Moody′s KMV Company, 1999:165-172.

[2] Dwyer D, LI Zan, QU Shi-sheng,etal. CDS-implied EDFTMcredit measures and fair-value spreads [R]. UK:Palgrvae MacMillan, 2010.

[3] Lee Wo-chiang. Redefinition of the KMV model′s optimal default point based on genetic algorithms-Evidence from Taiwan [J]. Expert Systems with Applications, 2011, 38(8):10107-10113.

[4] Dionysiou D, Lambertides N, Charitou A,etal. An alternative model to forecast default based on Black-Scholes-Merton model and a liquidity proxy [R]. Cyprus:Department of Public and Business Administration, University of Cyprus, 2008.

[5] Korablev I, Dwyer D. Power and Level Validation of Moody′s KMV EDFTMCredit Measures in North America, Europe, and Asia [M]. Sanfrancisco:Moody′s KMV Company, 2007.

[6] Duffie D, Wang K. Multi-period corporate failure prediction with stochastic covariates [R]. Palo Alto:Stanford University, 2004.

[7] Merton R C. On the pricing of corporate debt:the risk structure of interest rates [C] // American Finance Association Meetings. New York:American Finance Association, 1973.

[8] Black F, Scholes M. The pricing of options and corporate liabilities [J]. The Journal of Political Economy, 1973, 81(3):637-654.

[9] Alizadeh F, Goldfarb D. Second-order cone programming [J]. Mathematical Programming, 2003, 95(1):3-51.

Determination of KMV model′s optimal default point based on genetic algorithm

FENG Jing-hai*, TIAN Jing

( School of Mathematical Sciences, Dalian University of Technology, Dalian 116024, China )

Credit evaluation plays an important role in modern market economy as the main force in the social supervision and risk identification of default. Based on the data of Chinese listing corporation, combined with genetic algorithm, the optimal default point in the classical KMV model is redefined. The applicable results indicate that the percentage of correctness of the improved model is higher than the original one, in other words, the improved KMV model is more suitable for application in China.

option pricing; KMV; genetic algorithm; credit risk

1000-8608(2016)02-0181-04

2015-05-20；

2016-01-06．

冯敬海*(1970-)，男，教授，硕士生导师，E-mail:math109@163.com；田 婧(1991-)，女，硕士生，E-mail:tianjing11164@163.com.

F830.9

A

10.7511/dllgxb201602011