含弱界面结构断裂分析中辛方法

徐 新 生， 程 显 贺， 徐 成 辉， 周 震 寰

( 1.大连理工大学 工程力学系, 辽宁 大连 116024；2.大连理工大学 工业装备结构分析国家重点实验室, 辽宁 大连 116024 )



含弱界面结构断裂分析中辛方法

徐 新 生*1,2， 程 显 贺1,2， 徐 成 辉1,2， 周 震 寰1,2

( 1.大连理工大学 工程力学系, 辽宁 大连 116024；2.大连理工大学 工业装备结构分析国家重点实验室, 辽宁 大连 116024 )

基于哈密顿体系，提出了一种分析含弱界面弹性材料断裂问题的辛方法．通过引入对偶变量，建立基本问题的哈密顿体系．在该体系下，问题的解可被辛本征解的级数形式所表示．利用辛本征解之间的辛共轭正交关系，以及裂纹面条件、弱界面条件和结构外边界条件，可确定辛本征解级数的待定系数，从而得到问题的解．这样，可以获得Ⅰ型和Ⅱ型广义应力强度因子解析表达式．数值结果揭示了各种边界条件对应力强度因子的影响，同时也表明该方法对复杂的混合边界条件问题更有效．

哈密顿体系；辛方法；应力强度因子；弱界面

0 引 言

随着科学技术的发展，层状复合材料以其优良的力学性能被广泛应用于土木、机械、航空航天以及电子工程领域中．该类材料通常由一种或多种材料通过黏合等方式构成，在使用中易产生界面裂纹，从而影响结构的整体性能以及寿命．目前，针对层状复合材料界面断裂的研究多集中于强连接界面情况，即假定材料界面位移和应力连续．然而，由于制造技术等原因，各层材料间界面往往达不到强连接的黏结强度．此外，对某些复合材料结构层裂的修复也不能作为强连接问题．因此，考虑具有弱连接界面的断裂问题具有重要的实际意义．

目前对弱界面问题研究中多采用弹簧模型[1-5]，即界面上的应力连续、位移间断，并且应力与间断位移间存在比例关系．Zhong等[1]和Li等[3]使用傅里叶变换及奇异积分方程分析了垂直于弱连接界面的Ⅰ型深埋裂纹问题和平行于弱连接界面的Ⅲ型裂纹问题．Chen等[2]采用状态空间法给出了简支状态下弱连接压电层合板自由振动的精确解．Wang等[6]利用边界元法讨论了具有弱连接界面的Ⅲ型裂纹问题．薛雁等[7]研究了具有弱连接界面的压电夹层结构在反平面变形情况下的端部效应．从上述文献可以看出，现有关于弱连接界面断裂问题的文献非常有限，针对裂纹修复问题甚至尚未提及．因此，对该类界面裂纹及其修复效果的评估研究是必要的．

Zhong针对弹性力学问题首次提出哈密顿体系下的辛方法[8]，突破传统拉格朗日求解体系的限制，将问题在哈密顿体系下进行研究，并形成比较完整的求解方法．后来此方法被推广到许多其他研究方向[9-11]．本文将哈密顿体系辛方法拓广到弱界面断裂问题中，在哈密顿体系下，利用对偶变量构造基本控制方程，将问题归结为本征值和本征解问题，直接得到界面裂纹的应力强度因子，以评估含裂纹结构的安全性．

1 基本问题

(1)

其中k1(r)与k2(r)分别为连接界面的法向与切向界面参数．裂纹面(θ=±π)处的边界条件为[1-5]

(2)

其中k3(r)与k4(r)分别为裂纹面的法向与切向界面参数．这里需要特别指出，k1(r)=k2(r)=∞表示界面强连接情况；k3(r)=k4(r)=0表示自由裂纹面情况，即裂纹未做修复处理情况，k3(r)=k4(r)≠0表示裂纹面被黏结修复，等效为弱连接．

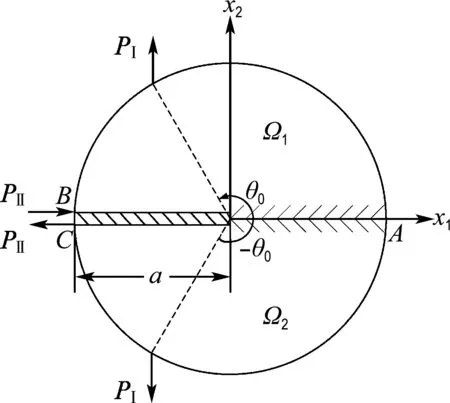
图1 含边裂纹区域

外边界条件可归结为位移条件和应力条件，它们分别可以表示为

(3)

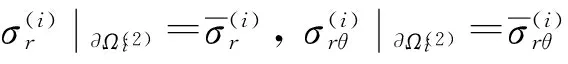
(4)

(5)

(6)

其中∂r≡∂/∂r，∂θ≡∂/∂θ．

2 问题的哈密顿体系描述

为了导入哈密顿体系，引入广义坐标ξ=lnr，记∂ξ≡r∂r．将ξ模拟为“时间”，并定义

f.

(7)

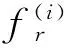
L(i)，利用哈密顿变分原理可以得到哈密顿对偶方程：

(8)

哈密顿体系下材料连接界面(θ=0)处的边界条件如下[4]：

(9)

其中sθ=rσθ，k1与k2分别为连接界面的法向与切向界面参数．裂纹面(θ=±π)处的边界条件如下[4]：

(10)

这里k3与k4分别为裂纹面的法向与切向界面参数．

3 辛本征解和辛共轭正交关系

不考虑体力，哈密顿方程式(8)可改写为

(11)

采用广义分离变量法

Ψ(i)(ξ,θ)=ψ(i)(θ)eμξ

(12)

则有

(13)

由文献[8]可知本征解形式如下：

(14)

可见本征解(14)中含有8个未知数，由方程(9)可得

(15)

其中

将式(14)代入裂纹面条件(10)，可得

(16)

其中

由式(15)和(16)可得

Kφ(1)=0

(17)

(18)

当区域Ω1与区域Ω2材料相同时，即E=E1=E2，υ=υ1=υ2时，上式可化简为

[-4Eμcos(μπ)(k1+k3)+sin(μπ)×

(E2μ2-16k1k3)][-4Eμcos(μπ)(k2+k4)+

sin(μπ)(E2μ2-16k2k4)]μ2sin2(μπ)=0

(19)

式(14)的本征值可以利用上式确定．

若μm是式(13)本征值，则-μm亦是其本征值．故本征值可分成以下两组：

(20)

则本征解满足辛共轭正交关系：

(21)

4 数值方法

由于β-类本征解在r=0处位移奇异，该类解为非物理解，只需考虑α-类本征解．通解Ψc可以写为

(22)

这里dj为待定系数．在r=a处的边界条件为

(23)

利用通解(22)，边界条件(23)可以改写为

(24)

利用式(24)和辛共轭正交关系(21)有

(25)

其中

至此，通解的待定系数dj可以由式(25)的线性代数方程组确定．

5 数值结果分析

数值模拟中主要考虑以下两种情况．

情况1： k1≠0，k2≠0，k3=0，k4=0，即裂纹面自由，材料界面弱连接．

情况2： k1≠0，k2≠0，k3≠0，k4≠0，即裂纹面弱连接，材料界面弱连接．

5.1 弱连接界面的奇异性分析

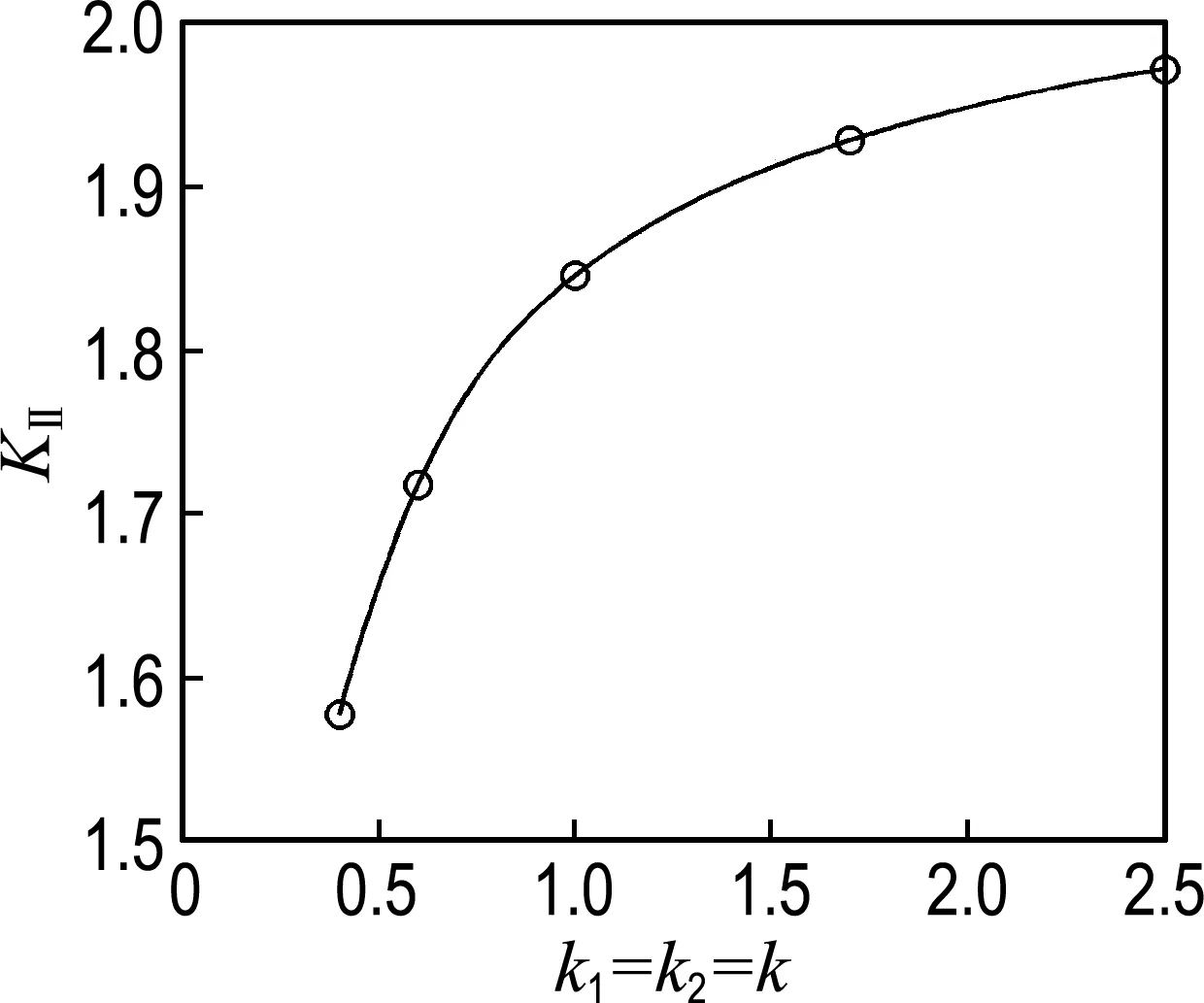
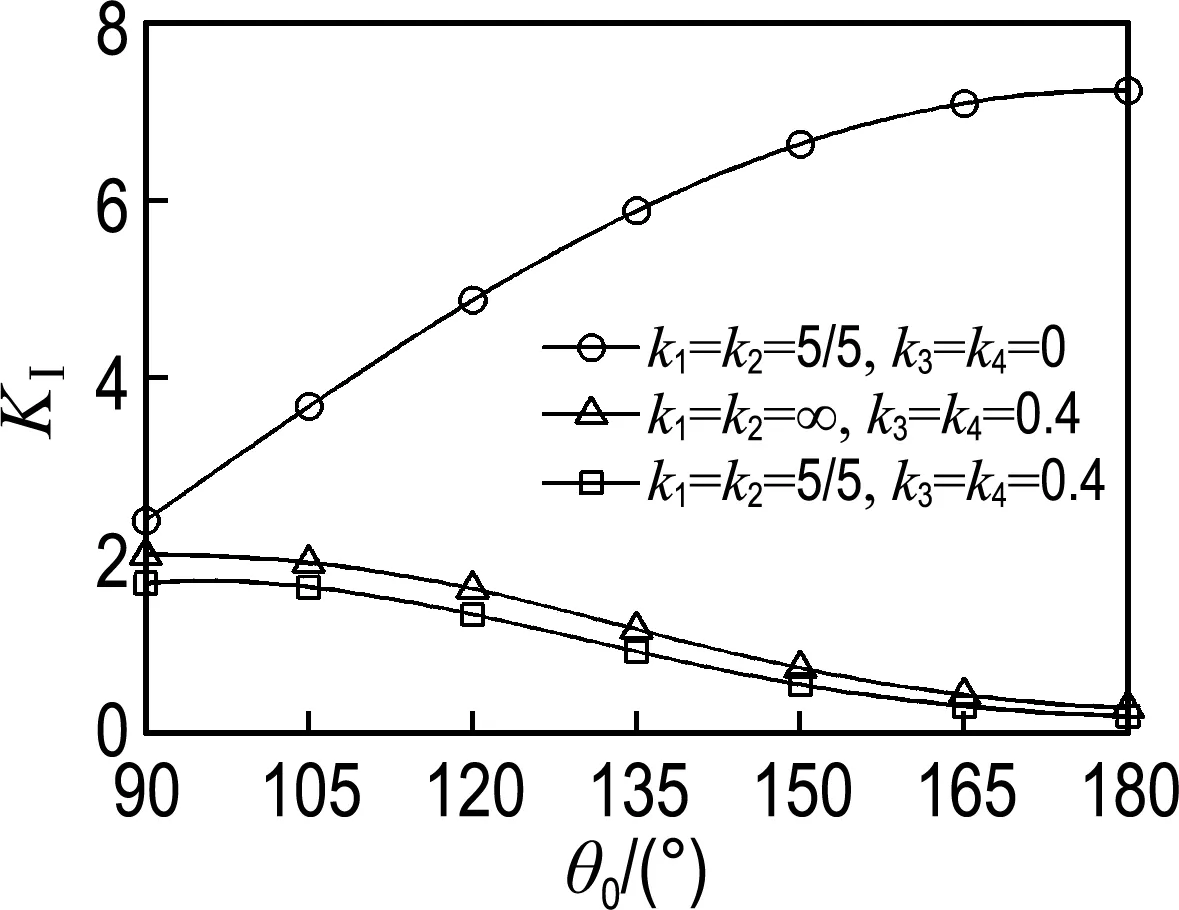
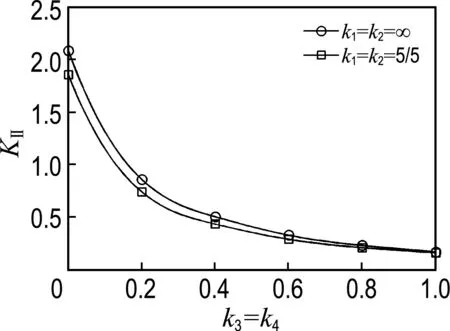
首先，讨论裂纹面自由，材料界面弱连接的情况1的奇异性问题．裂纹尖端的奇异性可以通过-1

(26)

其中KⅠ和KⅡ分别为Ⅰ型和Ⅱ型广义应力强度因子．

表1 不同界面参数下的奇异性

5.2 弱连接界面在集中荷载作用下的问题

考虑所讨论的问题为圆形区域，如图2所示．有一对集中力作用在边界上，界面和裂纹面条件如情况1．PⅠ为作用在外边界±θ0处的对称单位集中力，PⅡ为作用在裂纹面上B、C点处的反对称单位集中力．

图2 弱连接界面圆盘受Ⅰ/Ⅱ型集中力作用情况

图3给出了受PⅠ单独作用(θ0=180°)产生的Ⅰ型广义应力强度因子随本征解项数的收敛性曲线．从图中可以看到，当本征解项数超过18项之后，界面强连接情况(k1=k2=∞)对应的KⅠ稳定收敛于理论值，说明本文方法的可靠性；界面弱连接(k1=k2=5/5)情况对应的广义应力强度因子KⅠ收敛值略低于强连接情况，这与物理现象一致．由此可见，该方法的收敛性较好．以下算例的计算均取26项辛本征解．

图3 收敛性与本征解项数的关系

图4给出对称荷载PⅠ作用位置θ0及界面参数k1=k2对Ⅰ型广义应力强度因子KⅠ的影响曲线．从图中可看出，KⅠ随θ0增大而增大．这种现象是由于荷载作用位置与裂纹尖端在裂纹面的投影距离增大所致．KⅠ随界面参数k1=k2增大而增大，即界面连接越牢固对应的KⅠ越大．且当k1=k2=∞时，当前解与理论解[12]非常吻合．

图4 自由裂纹面Ⅰ型广义应力强度因子

图5给出反对称荷载PⅡ作用下Ⅱ型广义应力强度因子KⅡ的变化情况．KⅡ随界面参数k1=k2增加而增大，当k1=k2=2.5时，KⅡ为1.971 8．另外可知，当k1=k2=∞时，KⅡ达到最大值2.068 7，可见k1=k2>2.5后KⅡ的变化不大．说明这种情况可以被近似视为强连接问题．

图5 自由裂纹面Ⅱ型广义应力强度因子

5.3 弱连接裂纹面受集中荷载作用问题

考虑图2所示的情况2．图6与7分别给出弱界面参数k1、k2、k3与k4对KⅠ及KⅡ的影响曲线．图6表明自由裂纹面(k3=k4=0)情况下，集中力作用位置越远离裂纹尖端KⅠ越大；而裂纹

图6 不同弱界面条件下Ⅰ型广义应力强度因子

图7 不同弱界面条件下Ⅱ型广义应力强度因子

修复后(k3=k4≠0)，KⅠ的变化趋势与自由裂纹面情况完全相反，且θ=0的连接界面参数k1与k2越大KⅠ也越大．这种现象说明，裂纹修复(弱连接)有利于实现止裂效果．图7表明反对称荷载作用下，KⅡ随弱界面参数k3与k4增大而减小，说明裂纹面连接越牢固，KⅡ就越小．且θ=0的界面参数k1与k2越大KⅡ也越大．该规律与物理现象一致．

5.4 弱连接界面的混合边界条件问题

最后，考虑情况1界面和裂纹且外边界为混合边界条件，如图8所示．不妨取

图9给出不同弱界面参数k1与k2和不同角度θ0对KⅠ的影响曲线．从图中观察到，当θ0=0°时，KⅠ达到极大值；当θ0>0°后，KⅠ急剧下降．图10给出KⅡ随角度θ0的变化曲线．该图表明，当θ0=-45°时，KⅡ达到极大值；且在θ0=[-90°，90°]，界面参数k1与k2越大，KⅡ的绝对值亦越大．

图8 弱连接界面圆盘受混合边界条件作用

图9 混合边界条件下Ⅰ型广义应力强度因子

图10 混合边界条件下Ⅱ型广义应力强度因子

6 结 语

本文将辛方法应用于具有弱界面的断裂分析中．在哈密顿体系下，可直接得到界面裂纹的应力场、位移场及广义应力强度因子的解析表达式．数值结果表明，辛方法可以有效求解弱界面断裂问题，方法具有良好的收敛性，尤其对复杂边界条件同样有效．裂纹面为自由表面时，相同外边界条件作用下，材料界面参数越大，相应的广义应力强度因子越大．然而，该广义应力强度因子不会高于强连接界面问题的广义应力强度因子；反之，裂纹面亦为弱连接时，相应的广义应力强度因子较之裂纹面为自由表面情况小得多，说明裂纹经过修复之后，可以承载更大的荷载．

[1] ZHONG Xian-ci, LI Xian-fang, Lee Kang-yong. Analysis of a mode-Ⅰ crack perpendicular to an imperfect interface [J]. International Journal of Solids and Structures, 2009, 46(6):1456-1463.

[2] Chen W Q, Lee K Y. Exact solution of angle-ply piezoelectric laminates in cylindrical bending with interfacial imperfections [J]. Composite Structures, 2004, 65(3-4):329-337.

[3] LI Yong-dong, Lee Kang-yong. The shielding effect of the imperfect interface on a mode III permeable crack in a layered piezoelectric sensor [J]. Engineering Fracture Mechanics, 2009, 76(7):876-883.

[4] 刘承斌,吕朝锋. 具有弱界面特性叠层压电球壳的自由振动[J]. 固体力学学报, 2012, 33(3):317-324. LIU Cheng-bin, LV Chao-feng. Free vibration of multi-layered piezoelectric spherical shells with imperfect interfaces [J]. Chinese Journal of Solids Mechanics, 2012, 33(3):317-324. (in Chinese)

[5] 但 敏. Hamilton体系下层合板弱粘接模型的应用[J]. 应用数学和力学, 2013, 34(1):72-84.

DAN Min. Application of composite laminated plates with bonding imperfection in Hamilton system [J]. Applied Mathematics and Mechanics, 2013, 34(1):72-84. (in Chinese)

[6] WANG Xue, Ang Whye-teong, FAN Hui. Micro-mechanics models for an imperfect interface under anti-plane shear load:Hypersingular integral formulations [J]. Engineering Analysis with Boundary Elements, 2012, 36(12):1856-1864.

[7] 薛 雁,刘金喜. 反平面变形下弱界面压电夹层结构的圣维南端部效应[J]. 工程力学, 2013, 30(6):41-46.

XUE Yan, LIU Jin-xi. Saint-Venant end effect for anti-plane deformation of piezoelectric sandwich structures with weak interfaces [J]. Engineering Mechanics, 2013, 30(6):41-46. (in Chinese)

[8] ZHONG Wan-xie. Duality System in Applied Mechanics and Optimal Control [M]. Boston:Kluwer Academic Publishers, 2004.

[9] ZHOU Zhen-huan, XU Xin-sheng, Leung A Y T,etal. Stress intensity factors and T-stress for an edge interface crack by symplectic expansion [J]. Engineering Fracture Mechanics, 2013, 102:334-347.

[10] XU Xin-sheng, CHENG Xian-he, ZHOU Zhen-huan,etal. An analytical approach for the mixed-mode crack in linear viscoelastic media [J]. European Journal of Mechanics-A/Solids, 2015, 52:12-25.

[11] Leung A Y T, XU Xin-sheng, ZHOU Zhen-huan,etal. Analytic stress intensity factors for finite elastic disk using symplectic expansion [J]. Engineering Fracture Mechanics, 2009, 76(12):1866-1882.

[12] Wu X R. The arbitrarily loaded single-edge cracked circular disc; accurate weight function solutions [J]. International Journal of Fracture, 1991, 49(4):239-256.

A symplectic method for fracture analysis of structure with weak interface

XU Xin-sheng*1,2, CHENG Xian-he1,2, XU Cheng-hui1,2, ZHOU Zhen-huan1,2

( 1.Department of Engineering Mechanics, Dalian University of Technology, Dalian 116024, China；2.State Key Laboratory of Structural Analysis for Industrial Equipment, Dalian University of Technology,Dalian 116024, China )

Based on Hamiltonian system, a symplectic method for analyzing the fracture problem of weak interface between two elastic media is presented. By introducing the dual variables, the Hamiltonian system is constructed, then the solution of the problem can be represented by series form of the symplectic eigensolutions. By means of the symplectic adjoint orthogonal relationship between symplectic eigensolutions, together with crack surface conditions, weak interfacial conditions and external boundary conditions of structure, the undetermined coefficients of the symplectic series can be determined. Therefore, the solution is obtained. In this way, the generalized stress intensity factors of Mode Ⅰ and Mode Ⅱ are expressed analytically. The numerical results reveal the influence of various boundary conditions on the stress intensity factors, and also show that the method is more effective for complex mixed boundary conditions.

Hamiltonian system; symplectic method; stress intensity factor; weak interface

1000-8608(2016)02-0111-07

2015-07-14；

2016-01-10．

国家自然科学基金资助项目(11372070，11302042)；“九七三”国家重点基础研究发展计划资助项目(2014CB046803)；中央高校基本科研业务费专项资金资助项目(DUT14LK41，DUT14RC(4)39).

徐新生*(1957-)，男，博士，教授，博士生导师，E-mail:xsxu@dlut.edu.cn.

TP273

A

10.7511/dllgxb201602001