时变波动率和随机利率模型下的动态投资研究

孙瑞娇，杜晓婷

(山东科技大学 数学与系统科学学院,山东 青岛 266590)



时变波动率和随机利率模型下的动态投资研究

孙瑞娇，杜晓婷

(山东科技大学 数学与系统科学学院,山东 青岛 266590)

在金融市场中，假设风险资产价格的波动率随时间的变化而变化，它的函数表达式由随机环境下的波动率去掉随机项的部分确定，无风险利率是随机的，用Hull-White随机利率模型来刻画，根据动态规划中的Bellman最优性原理，建立了基于幂效用函数的风险资产和无风险资产的动态投资组合模型，给出了使期望效用最大化的最优投资策略.

时变波动率；Hull-White随机利率模型；动态投资组合；Bellman最优性原理；期望效用最大化

投资组合是投资者将资金投资于风险资产和无风险资产的组合，它的目的在于分散风险，使终端财富最大化.自Markowitz提出分散投资和效率投资组合理论[1,2]以来,在最优投资组合问题上出现了许多显著的研究成果，尤其是波动率随机化或无风险利率随机化下的投资组合.对于随机利率下的投资组合，国内外学者大部分研究了Ho-Lee随机利率模型、Vasicek随机利率模型或Cox-Ingersoll-Ross(CIR)随机利率模型[3～6]下的投资组合问题,而很少与具体的时变波动率或随机波动率结合来研究投资组合问题.

Hull-White随机利率模型作为Ho-Lee随机利率模型的推广模型，比其它随机利率模型能更好地匹配当前的利率期限结构,并且它所描述的利率过程是一个无套利的Markov过程[7～11]，具有较好的性质和研究价值.对于风险资产价格的波动率，有一种随机波动率，其过程遵循几何布朗运动，可以保证波动率的非负性[12].不确定性下的理性决策有3种准则：一是数学期望最大化准则，二是期望效用准则，三是后期望效用准则.20世纪50年代，Von Neumann和Morgenstern提出了期望效用函数理论，针对金融市场中的投资组合问题，依据期望效用准则，在不确定的情况下，为了最大化期望效用，必须事先做出适当的投资决策[13，14].

本文在常浩[15]提出的 Ho-Lee利率模型下的动态投资组合的基础上,采用Ho-Lee利率的推广模型——Hull-White随机利率模型，并与具体的时变波动率相结合，研究动态投资组合问题.应用期望效用函数理论，建立了幂效用函数下的动态投资组合模型，并给出了最优投资策略的显示表达式.

1 投资组合模型

假定投资者选择了金融市场中的两种资产进行投资，一种是无风险资产，比如通常情况下的政府债券，另一种是风险资产，比如股票或衍生金融产品，投资周期为[0,T].用P(t)，S(t)分别表示无风险资产和风险资产在t时刻的价格，它们的价格过程对应着下面的2个方程：

(1)

(2)

其中,r(t)为t时刻的无风险利率，λ(t)为风险资产在t时刻的风险溢价，σ(t)为风险资产价格在t时刻的波动率，B(t)为一维的标准布朗运动.

(3)

根据Ito公式可以得到

其中,σ0为风险资产价格在0时刻的波动率，β,η为常数.

对于无风险利率r(t)，假定它是随机的，应用Hull-White随机利率模型，满足的随机微分方程如下：

(4)

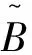
(5)

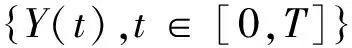
结合式(1)、(2)得到:

(6)

来刻画.于是建立以下的动态投资组合模型：

(7)

2 最优投资策略

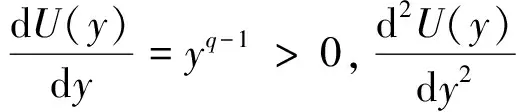
定义值函数

(8)

结合式(5)、(6)，根据Bellman最优性原理[15]，值函数V(t,r,y)对应下面的HJB方程

(9)

其中,Vt,Vy,Vr,Vrr,Vry,Vyy分别是V(t,r,y)关于t,r,y的一阶偏导与二阶偏导数.对式(9)左边大括号内的部分关于x(t)求偏导数，由于是凹规划问题，一阶最优性条件也是充分条件.进而由一阶最优性条件得：

(10)

从而得最优解

(11)

这是模型的隐式解.

将式(11)代入式(9)可以得到：

(12)

以下定理给出最优投资策略的显示表达式：

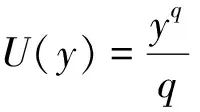
(13)

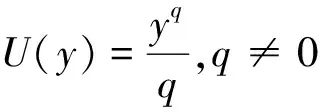
将它们代入式(12)可得

(14)

又因为

其中,M′(t)，N′(t)分别表示它们关于t的导数，代入式(14)得

(15)

消除式(15)对r的依赖性可以得到下面两个方程：

解得

所以

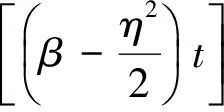
3 小结和展望

在时变波动率和Hull-White随机利率模型下的最优投资策略x*(t)与波动率参数β，η和随机利率参数α(t)，σr有关，而与随机利率参数θ(t)无关.因此波动率与利率共同影响着投资者做何种决策.本文所建立的动态投资组合模型是在时变波动率和随机利率下建立的，在随机波动率和随机利率下也可以建立相应的动态投资组合模型，求得最优解.

[1] 埃尔顿.现代投资组合理论和投资分析[M].6版.北京:中国人民大学出版社,2006.

[2] 张卫国.现代投资组合理论[M].北京：科学出版社,2007.

[3] 皮里沃.随机利率模型及相关衍生品定价[M].伟晓，译.天津：南开大学出版社，2010.

[4] Hao R,Liu Y,Wang S.Pricing Credit Default Swap under Fractional Vasicek Interest Rate Model[J].Journal of Mathematical Finance,2014,4(1):10-20.

[5] Inoue A,Moriuchi S,Nakamura Y.A Vasicek-Type Short Rate Model With Memory Effect[J].Stochastic Analysis & Applications,2015,33(6):1068-1082.

[6] Alfonsi A.High order discretization schemes for the CIR process:Application to affine term structure and Heston models[J].Mathematics of Computation,2010,79(269):209-237.

[7] 沈传河,王向荣.Hull-White随机利率模型在债券价值分析中的应用[J].统计与决策,2005(18):21-23..

[8] Lech A.Grzelak,Cornelis W.Oosterlee,Sacha Van Weeren.Extension of stochastic volatility equity models with the Hull-White interest rate process[J].Quantitative Finance,2012,12(1):89-105.

[9] Kim J H,Yoon J H,Yu S H.Multiscale Stochastic Volatility with the Hull-White Rate of Interest[J].Journal of Futures Markets,2014,34(9):819-837.

[10] Leonard Tchuindjo.Pricing of Multi-Defaultable Bonds with a Two-Correlated-Factor Hull-White Model[J].Applied Mathematical Finance,2007,14(1):19-39.

[11] Cappé O,Moulines E,Rydén T.Inference in hidden Markov models[M].New York:Springer,2005.

[12] 韩立岩,泮敏.基于奈特不确定性随机波动率期权定价[J].系统工程理论与实践,2012(6):1175-1183.

[13] Rabin M.Risk aversion and expected-utility theory:A calibration theorem[J].Econometrica,2000,68(5):1281-1292.

[14] 张新丽，张璐，王欣.风险投资并购退出行为的演化博弈分析[J].辽宁师范大学学报：自然科学版，2013,36(3)：323-328.

[15] 常浩.Ho-Lee利率模型下多种风险资产的动态投资组合[J].数理统计与管理,2015，34(3)：561-570.

[16] 雍炯敏，楼红卫.最优控制理论简明教程[M].北京：高等教育出版社，2006.

(责任编辑：张冬冬)

Research on dynamic portfolio of time-varying volatility and stochastic interest rate mode

SUN Ruijiao,DU Xiaoting

(Institute of Mathematics,Shandong University of Science and Technology,Qingdao Shandong 266590,China)

In the financial markets,volatility is assumed that the price of risky asset changes over time and its function expression is determined by the stochastic volatility without the part of a random item.The non-risk interest rate is random,with Hull-White stochastic interest rate models to describe.The paper,based on dynamic programming in the Bellman optimality principle,establishes a dynamic portfolio model based on a power utility function and obtains the implicit solution of optimal investment strategies.And finally then show the explicit expressions of optimal investment strategy and the corresponding conclusions.

timevarying volatility;Hull-White stochastic interest rate model;dynamic portfolio;Bellman principle of optimality;expected utility maximization

2016-04-21

孙瑞娇(1991-),女，山东聊城人，山东科技大学数学与系统科学学院硕士研究生.

F832.48；O211.6

A

1008-2441(2016)04-0001-05