基于牛顿迭代法的椭圆近似画法误差分析

周亚辉

(辽宁轨道交通职业学院，辽宁 沈阳 110023)

基于牛顿迭代法的椭圆近似画法误差分析

周亚辉

(辽宁轨道交通职业学院，辽宁 沈阳 110023)

四心圆法是用四段圆弧拼接成近似椭圆。由于其对称性，取图形的1/4为研究对象，利用二分法求解方程组，得出两段圆弧拼接点坐标值；分别用两段圆弧的极径和实际椭圆中相应的极径进行长度误差分析，列出两段圆弧与椭圆极坐标方程，使用牛顿迭代法，求出圆弧与实际椭圆的极径长度最大误差值；计算出近似椭圆与实际椭圆面积，求出面积误差值。在编程软件中，根据所得数学模型编制计算器，计算结果列表对比分析，得出四心圆法作近似椭圆的误差结论。

椭圆；牛顿迭代法；计算器；误差分析

现实生活中，使用直尺和圆规手工作图，不可能画出精确的椭圆。用若干段圆弧拼接成近似椭圆是一个自然的想法，椭圆的近似画法在数学(制图)、天文(轨道分析)、艺术和建筑(如石拱门)设计中曾有广泛应用[1]。使用四心圆法画近似椭圆是常见的方法，简化了椭圆的画法，易于通过尺规作图实现，但能否准确地代替椭圆，在此还需对四心圆法作椭圆进行误差分析。

1　四心圆法作椭圆

椭圆有两条相互垂直且对称的轴，即长轴和短轴，当长轴和短轴为已知时，用四心圆法画椭圆，其步骤[2]如下：

(1) 画出相互垂直且平分的长轴AB与短轴CD；

(2) 连接AC，并在AC上取CE=OA-OC，如图1(a)所示；

(3) 作AE的中垂线，与长、短轴分别交于O2、O3，再作对称点O1、O4，如图1(b)所示；

(4) 以O1、O2、O3、O4各点为圆心，O2C、O4D、O3A、O1B为半径分别画弧，即得近似椭圆，如图1(c)所示。

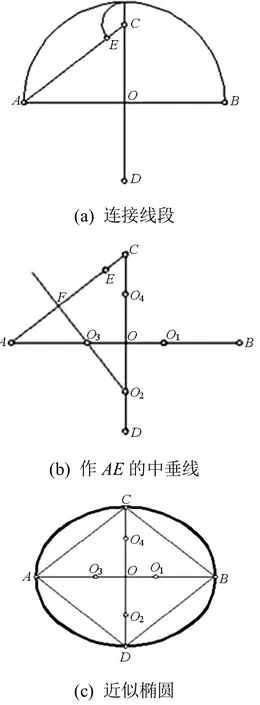
图1　四心圆法画椭圆

2　数学模型

王国顺和唐立波[3]介绍了圆弧拟合椭圆的误差分析没有精确理论解析。利用图形学理论，研究极径误差大小来分析圆弧与实际椭圆的近似程度，由于椭圆是对称图形，在研究其近似画法极径长度误差时，只研究图形的1/4即可，取第一象限图像为研究对象，并建立坐标系，如图2所示。

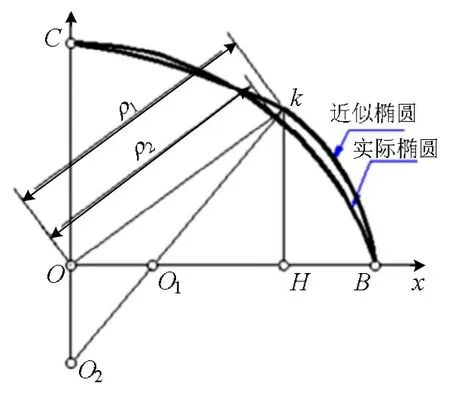
图2　1/4近似椭圆与实际椭圆

小圆弧是以O1为圆心，O1B为半径r，解析式为(x- a+ r)2+y2=r2；大圆弧是以O2为圆心，O2C为半径R，解析式为x2+(y- b+ R)2=R2；椭圆是以O为中心，长半轴长OB=a，短半轴长OC=b，解析式为。

极坐标是利用一点到原点的角度和距离来表示这一点的位置，取代横、纵坐标，经常用极坐标解决几何问题，在直角坐标系中(x, y)，x被 ρcosθ代替，y被ρsinθ代替，从而得到新的方程。其方程用来解决曲线问题，如椭圆曲线、纽线、螺线等，可以使解题更加清晰简便。

由小圆弧的极坐标方程得小圆弧极径长度：

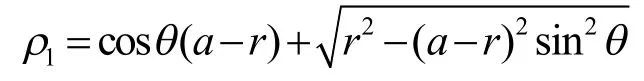
由椭圆的极坐标方程得椭圆极径长度：

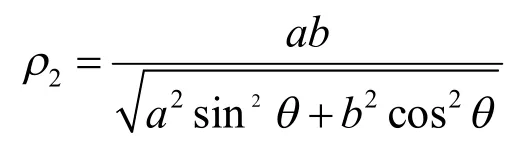
由大圆弧的极坐标方程得大圆弧极径长度：

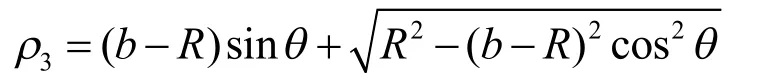
近似椭圆极径和实际椭圆中相应的极径长度误差：

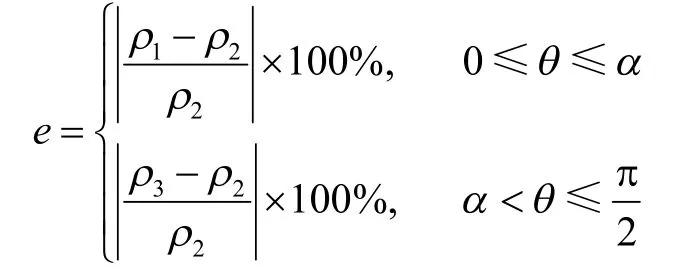
其中极角α=∠BOK。

由上式可知极径长度误差e是分段函数，大圆弧与小圆弧拼接点K是其分段点，所以需求解出K点坐标值，进而求得极角α值，对两段函数分别进行讨论计算，进而才能求得e的最大值。

欲求点K坐标值，需确定圆O1与圆O2的位置关系。圆与圆位置关系有5种，即相离、相切、相交、内切和内含，判断两圆的位置关系的步骤及其判断方法：①计算两圆的半径R，r；②计算两圆的圆心距O1O2，即d；③根据d与R，r之间的关系判断两圆的位置关系。

在图1(b)中，△AO3F∽△ACO，所以：

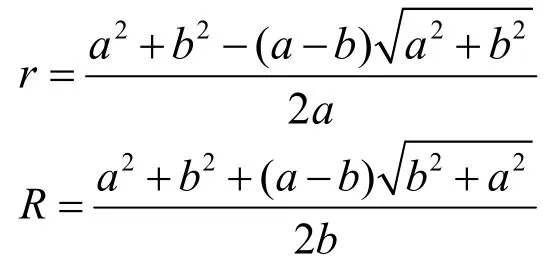
因：

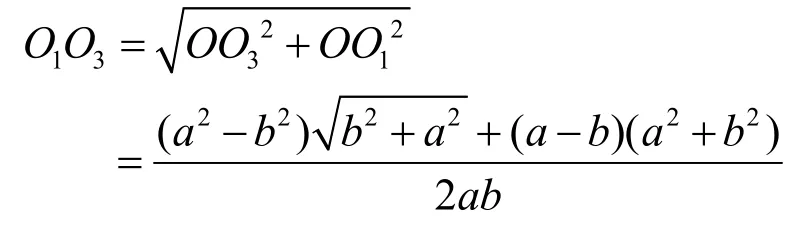
所以O1O3=R-r，即圆O1与圆O2相切，切点为K。在图2中，设K点坐标为(x, y)，△OO1O2∽△HO1K，所以：

由于K是切点，那么(x, y)满足小圆弧解析式，即：

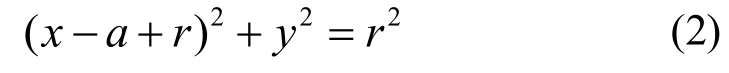
式(1)、(2)组成一个非线性方程组，利用二分法[4]求解方程，基本思想是：逐步将含根区间二等分，通过判别区间端点的函数值符号，进一步搜索含根区间，使含根区间长度缩小到足够小，从而求出满足给定精确度根的近似值，其运算简单、可靠、易在计算机上实现。

由于只讨论1/4图形，所以y取值区间为y=0 和y=b，在此区间进行迭代计算，求解出x与y值，从而求得。

在小圆弧段内，即极角θ∈(0,α)区间，极径长度误差，整理得，将其表达为隐函数，对其求导[5]求出极值点：。

式(3)是极角θ的超越方程，使用牛顿法[6]进行迭代求解。牛顿迭代法(New ton’s method)又称为牛顿-拉夫逊(拉弗森)方法(New ton-Raphson method)，其是牛顿在 17世纪提出的一种在实数域和复数域上近似求解方程的方法。基本思想是：将非线性方程f (x)=0逐步归结为某种线性方程来求解，把f (x)在点x0的某邻域内展开成泰勒级数：，取其线性部分(即泰勒展开的前两项)，并令其等于 0，即f( x0)+f′(x0)( x- x0)=0，以此作为非线性方程f( x)=0的近似方程，若f( x0)≠0，则其解为，这样，得到牛顿迭代法的一个迭代关系式：

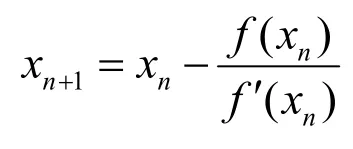
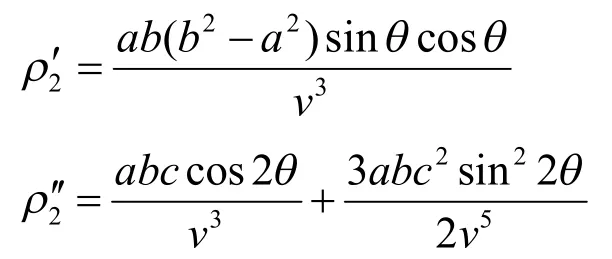
比较emax1与emax2的值，即可求出近似椭圆与实际椭圆的极径误差最大值。

椭圆面积S1=πab；近似椭圆是由圆弧段拼接而成的，所以：

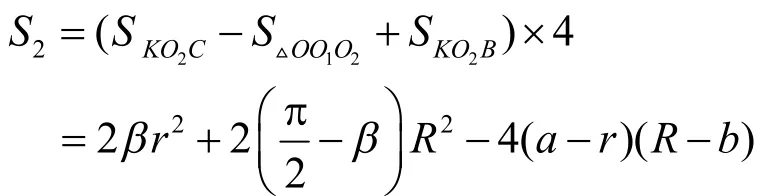
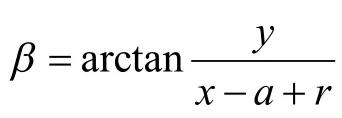
3　计算器

编程是为了借助计算机来达到某一目的或解决某个问题，而使用某种程序设计语言编写程序代码，并最终得到结果。随着计算机技术的发展和普及，数值分析的原理与方法在各学科中的应用越来越多，根据数学模型提出求解的计算方法，直到编出程序上机算出结果，并对计算结果进行分析。

根据推导出的数学模型，在编程软件中编写程序，生成椭圆近似画法误差计算器，如图3所示。

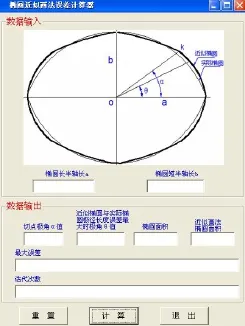
图3　计算器

输入椭圆长半轴和短半轴长参数，点击计算按钮，则输出结果。以a=25，b=12为例，计算结果如图4所示，通过46次迭代计算，大圆弧与小圆弧接点的极角α=19.883°，当极角θ=16.388°时，椭圆近似画法与实际椭圆的极径长度误差值最大，最大误差值为2.586%，实际椭圆面积S1=942.478，近似椭圆面积S2= 948.629，面积误差为0.653%。

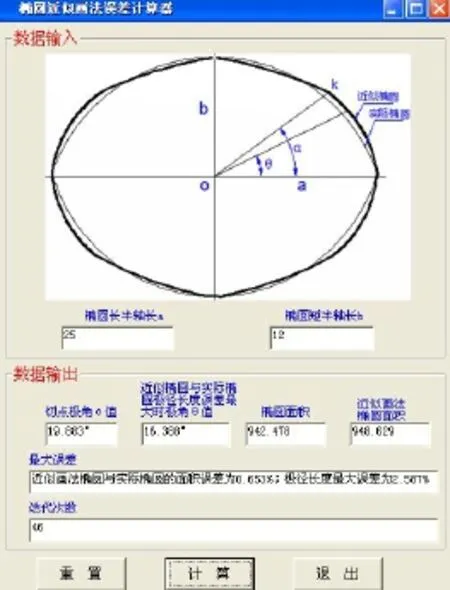
图4　计算结果

多次输入，可以点击重置按钮，文本框清除，可以重新输入。计算器的退出，有2种方法选择：①点击退出按钮；②点击界面的退出按钮，也可退出。

4　结　论

在计算器中，输入不同 a，b值，经计算输出结果，见表1。

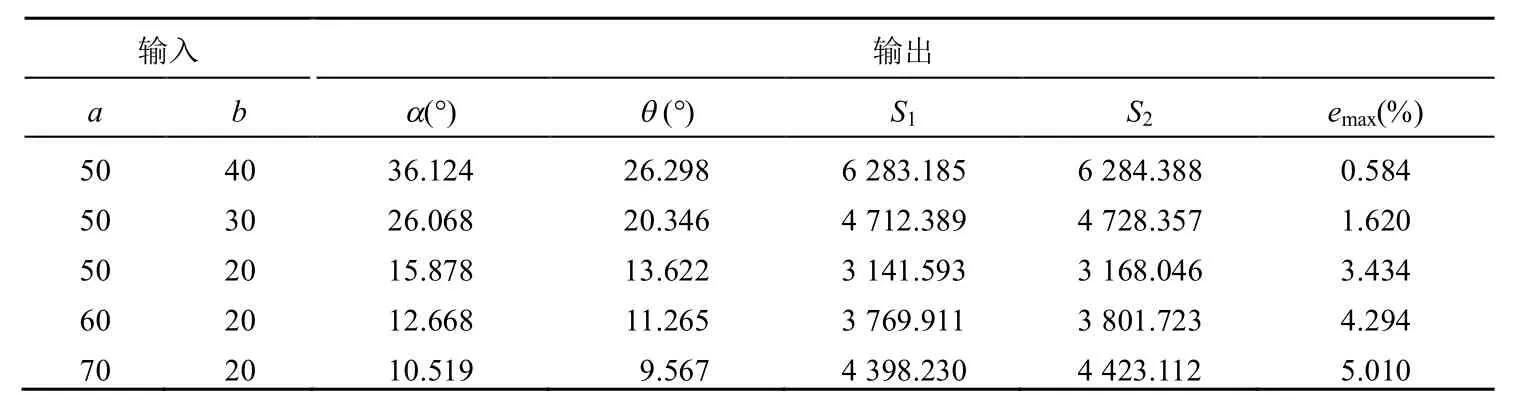
表1　计算结果

由表1可得如下结论：

(1)S2＞S1，说明近似椭圆比实际椭圆面积大，近似椭圆比实际椭圆更饱满。

(2)α ＞θ，说明极径最大偏差值永远发生在小圆弧段内，近似椭圆在大圆弧段内和实际椭圆拟合得较好。

(3)椭圆长半轴长a与短半轴长b越接近，即a/b值越接近1，极径长度误差越小，近似椭圆与实际椭圆拟合的越好。

[1] 曾振柄, 陈良育, 李志斌, 等. 偏差最小的四心圆近似椭圆作图法[J]. 图学学报, 2013, 34(1): 9-10.

[2] 王幼龙. 机械制图[M]. 北京: 高等教育出版社, 2007: 29.

[3] 王国顺, 唐立波. 八心圆弧拟合椭圆误差的理论解析及最优解[J]. 图学学报, 2014, 35(5): 697-703.

[4] 张铁, 闫家斌. 数值分析[M]. 北京: 冶金工业出版社, 2005: 78-79.

[5] 同济大学数学系. 高等数学[M]. 北京: 高等教育出版社, 2014: 86-88.

[6] 李庆扬, 王能超, 易大义. 数值分析[M]. 北京: 清华大学出版社, 2001: 276-277.

Error Analysis of Ellipse Based on New ton Iteration Method

Zhou Yahui

(Guidaojiaotong Polytechnic Institute, Shenyang Liaoning 110023, China)

The four-arcs method uses four arcs joining together similarly into an ellipse. Due to its symmetry, we take a quater graphics as the researching object and solve the equations by using dichotomy. Then we get the splicing point coordinates of the two pieces of circular arc. Then do error analysis with the actual ellipse in the two pieces of circular arc, and list the mathematical equations of the two pieces of circular arc and the ellipse polar. Then solve the actual maximum error value of the ellipse and the two pieces of circular arc with New ton iterative method. A fter that, figure out the approximate and actual ellipse areas, so as to work out the area error values. With the mathematical model, the calculator software is developed. It is concluded that the error of the approximated ellipse is solved through comparing the analysis list of calculating results.

ellipse; New ton iterative method; calculator; error analysis

TH 126

10.11996/JG.j.2095-302X.2016020189

A

2095-302X(2016)02-0189-04

2015-08-03；定稿日期：2015-11-03

周亚辉(1978–)，女，辽宁沈阳人，讲师，硕士。主要研究方向为机械工程。E-mail：sh6910@163.com