逼近三次B样条导矢曲线的四次Hermite插值样条

郭　啸， 韩旭里， 黄　琳

(1. 中南大学数学与统计学院，湖南 长沙410083；2. 长沙师范学院，湖南 长沙 410083)

逼近三次B样条导矢曲线的四次Hermite插值样条

郭啸1, 2， 韩旭里1， 黄琳2

(1. 中南大学数学与统计学院，湖南 长沙410083；2. 长沙师范学院，湖南 长沙 410083)

给出了形状可调的四次Hermite插值样条曲线的构造方法。四次样条曲线可提供额外的自由度用于调整曲线具有合理形状。利用导矢逼近使得四次Hermite样条曲线具有与三次B样条曲线相似的形状。通过最小化曲线间的导矢误差给出了确定自由度的方法，提出了四次Hermite插值样条曲线的构造方法。该方法增加了自由度控制曲线形状能更好满足保形要求。最后以实例对构造的四次Hermite样条曲线和标准三次Hermite插值样条曲线进行了比较。

Hermite插值样条；保形插值；形状可调

参数曲线的保形插值是计算机辅助几何设计中的重要研究内容。Hermite样条插值方法是构造保形曲线的重要方法之一[1]。关于Hermite插值曲线的构造方法，误差估计，形状保持以及插值应用已有较多研究成果[2-8]。利用Hermite插值方法，可对给定有序控制点Pi( i=0,1,…,n)及对应点的k阶导矢，构造出2k+1次的Hermite插值曲线，该曲线经过所有控制点且具有Ck连续性。当确定一阶导矢后可构造出最简单的三次Hermite插值曲线。但在某些情况下的三次Hermite插值曲线存在扭曲现象，对某些数据点集构造出的插值曲线存在重点，尖点或折叠的情况[9]。三次Hermite插值曲线没有额外自由度用以调整曲线形状，存在较大的应用局限性。提高插值阶次可以改善Hermite曲线的平滑性[10]，同时能增加自由度使曲线曲面具有更好的形状[11-12]。

本文提出一个构造可调整的C1连续四次Hermite样条插值方法。由于三次B样条曲线具有较好的几何特性[1,13]，在构造四次Hermite插值曲线时，应尽量接近三次B样条曲线形状。样条曲线的导矢反映了曲线的形状，因此本文通过设置导矢逼近的目标函数来确定自由度，给出了构造四次Hermite样条曲线的插值方法。最后通过实例，将构造的四次Hermite样条曲线和标准三次Hermite样条曲线的形状进行比较。

1　三次B样条曲线表示

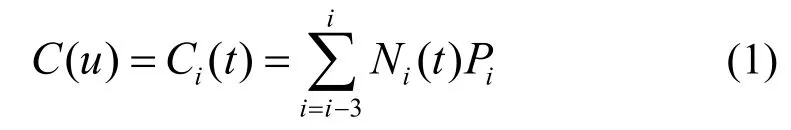
其中，

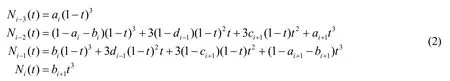
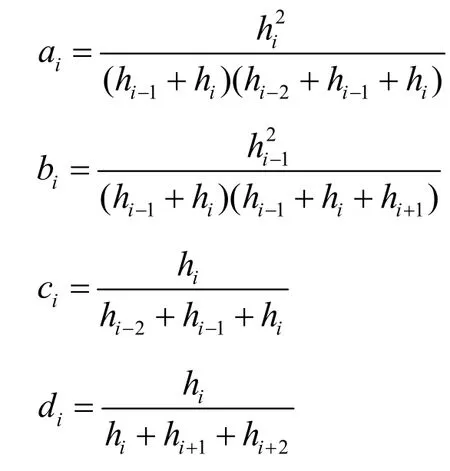
三次B样条曲线对控制多边形有很好的保形特性，其性质为：①凸包性；②几何不变性；③变差缩减性；④ui节点处二阶连续可微。

2　四次Hermite样条插值曲线的构造

或令导矢等于三次B样条曲线在节点处的导矢：

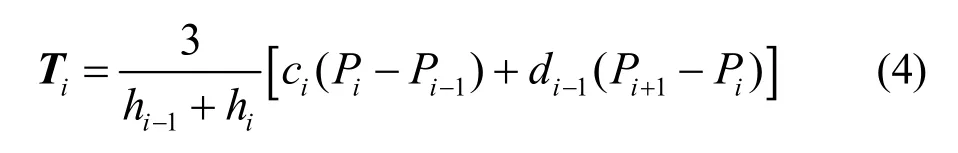
2.1四次Herm ite样条插值曲线定义

在控制点Pi, Pi+ 1之间可构造一段三次 Hermite曲线，使得S(t)满足插值条件：且，由此所构造的在u∈[a, b]上C1连续的曲线S(u)称为标准三次Hermite样条曲线。其是分段三次多项式，在每个小区间上的定义为：

将常用的标准三次Herm ite样条插值曲线升阶后可得到四次Hermite多项式：

本文采用新方法，对四次Hermite样条曲线引入用于调节形状的自由度参数，通过参数的不同取值实现曲线形状的调整。对任意u∈[ui, ui+1]，设，令Qi表示新增的自由度参数，将可调整的四次Hermite样条插值曲线定义为：

2.2形状参数的确定

由控制点Pi-1,Pi, Pi+1,Pi + 2所得到u∈[ ui+2, ui + 3]上的三次 B样条参数曲线Ci+2( t )具有良好的形状特性且相当逼近控制多边形的形状[14]，因此，希望选取合适的Qi值，能使控制点 Pi, Pi+ 1之间构造的四次Hermite样条插值参数曲线Si( t)形状尽量接近三次B样条曲线Ci+2( t )。两条曲线形状的接近程度可由曲线间一阶导矢曲线的距离：

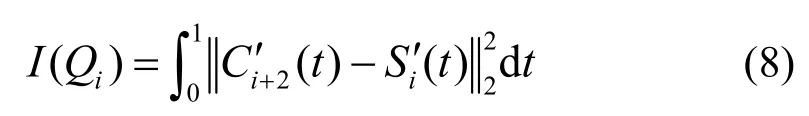
或者二阶导矢曲线的距离定义：

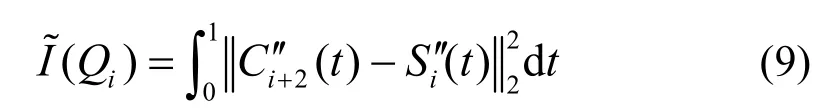
比较式(6)和式(7)可知，对任意的控制点及节点向量，都有，。以下分别按这两种情况确定形状参数来构造四次Hermite样条插值曲线。

(1) 一阶导矢距离最小。为了使曲线Si( t)是Ci+2( t )形状的最佳近似，将优化目标定义为二者一阶导矢曲线间的距离最小，即寻找Qi使得最小，等价于求。由函数求极值的必要条件有：

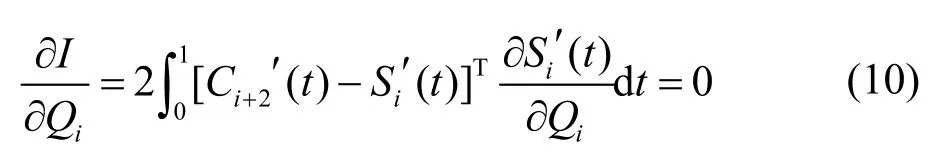
下面讨论如何求解式(10)。整理式(1)可得：

其中，

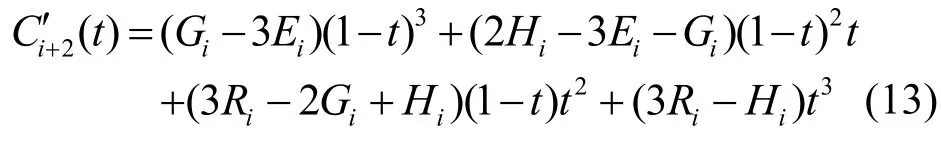
而

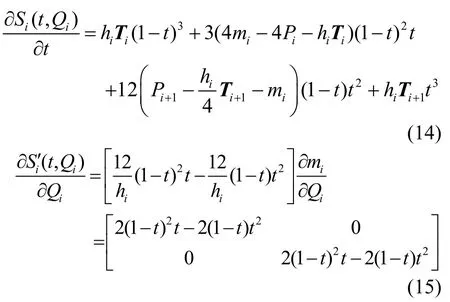
将式(11)～(15)代入式(10)整理得：

其中，

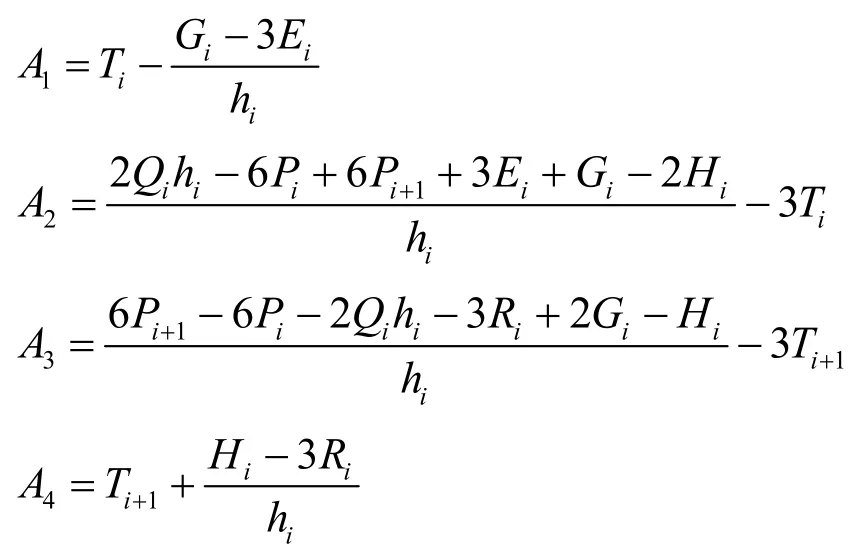
化简式(16)后求解得到：

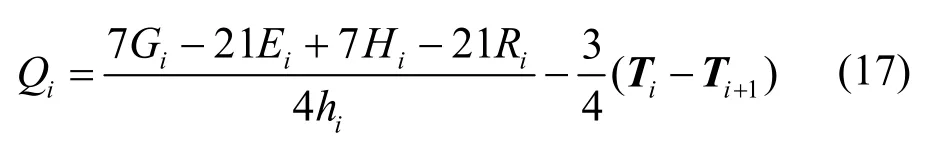
由于

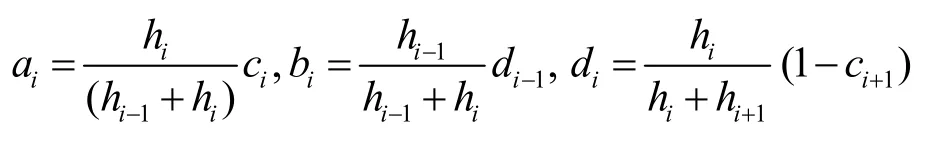
式(17)可进一步整理化简为：

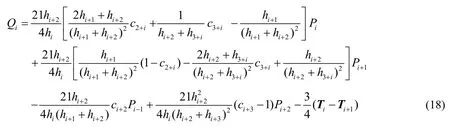
(2) 二阶导矢距离最小。通过最小化曲线间的二阶导矢距离来保证Si(t)在形状上近似Ci+2( t )，则需要寻找合适的Qi值使得最小。利用函数求极值的必要条件有：

需求解式(19)，将式(11)升阶后得：

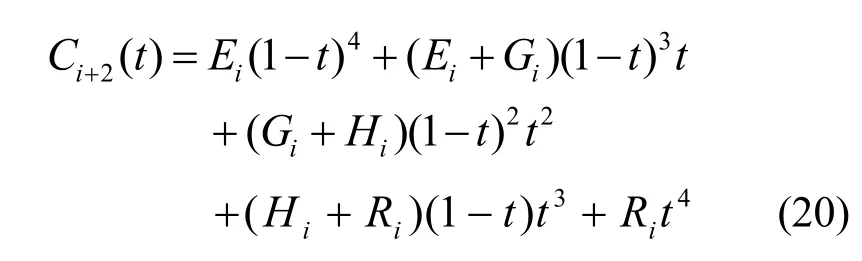
直接计算可得：

其中，

整理化简式(25)有：

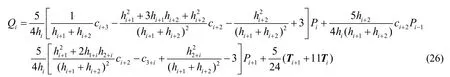
3　应用实例

表1中给出了例1～ 4的控制顶点和节点向量，实例中采用式(3)计算节点导矢。

根据例1中的数据，构造了逼近三次B样条曲线一阶导矢的四次Hermite样条插值曲线如图1点划线所示，逼近三次B样条曲线二阶导矢的四次Hermite样条插值曲线如图1细点曲线所示。将这两条四次Hermite插值曲线与图1实线所示的三次B样条曲线对比，从图形结果来看，逼近一阶导矢的四次Hermite插值曲线在峰值附近上升时变化率较缓，曲线下降后波动幅度较小，形状上更接近三次B样条所建议的形状。

在例2、3中，应用本文的新方法构造了逼近三次B样条曲线一阶导矢的四次Hermite样条插值曲线(见图2(b)与图3(b)中的实线曲线)。通过与标准的三次Herm ite样条曲线(见图2(a)与图3(a)中的虚线曲线)进行对比，在例2中构造的四次Herm ite样条曲线波动处幅度较小，例3中四次Hermite样条曲线整体上更接近插值数据点所形成的控制多边形。

例4中的控制点P2, P3, P4, P5用于构造闭合的四次Hermite插值曲线，可令 P1处的切矢T1与 P5处的切矢T5相等以保证闭合曲线的C1连续性。利用逼近三次B样条一阶导矢来构造的曲线如图4所示。从实例的细节效果来看，新方法构造的插值曲线对三次Hermite样条曲线的折叠程度有所改善。

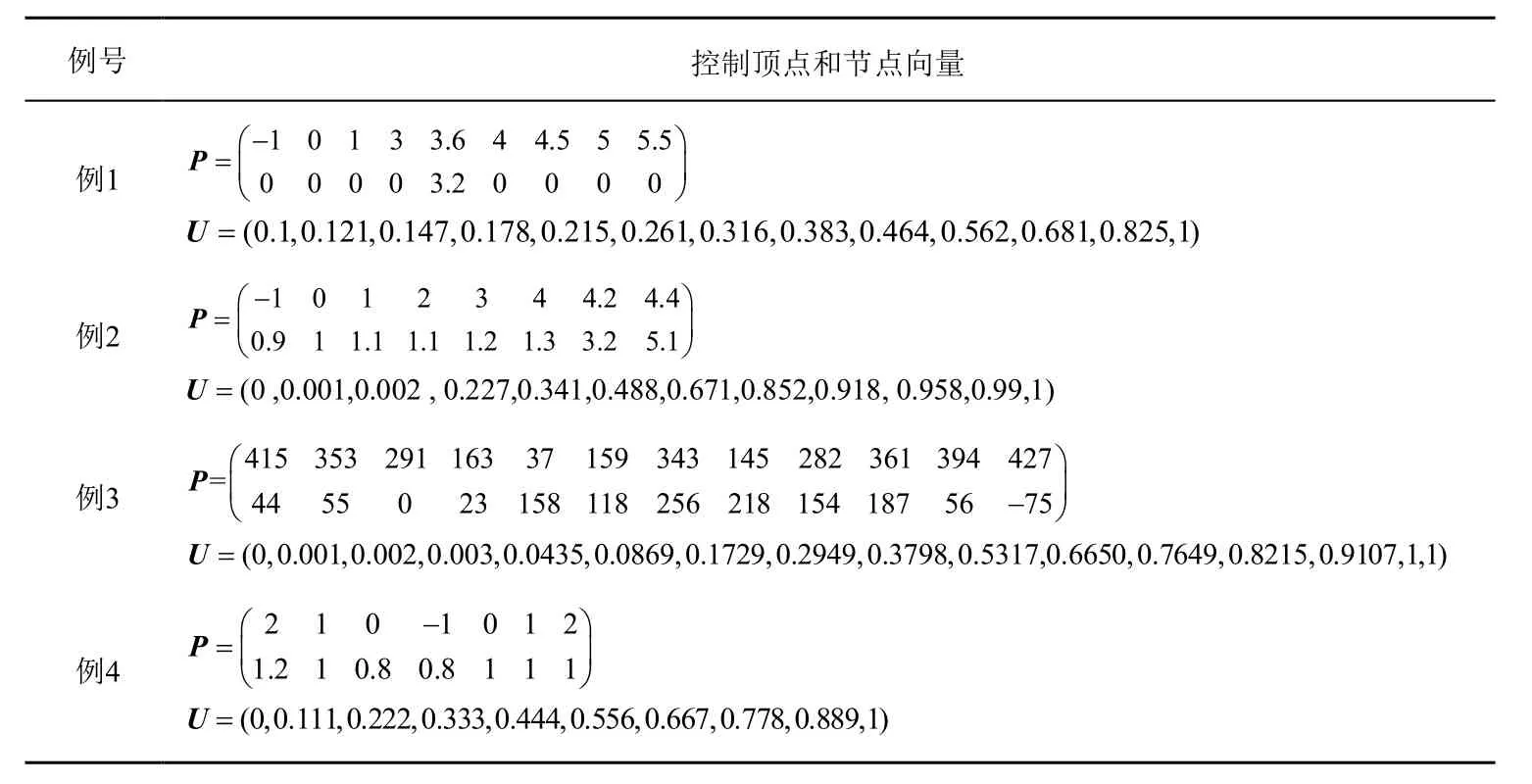
表1　例1～4控制点及节点数据

图1　数据点的样条插值曲线

图2　数据点的样条插值曲线

图3　数据点的样条插值曲线

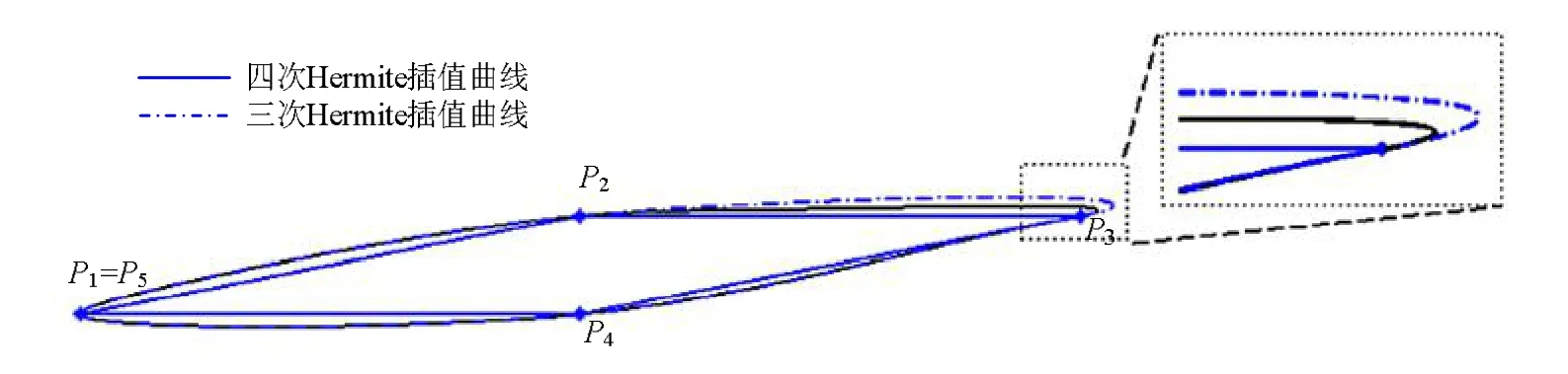
图4　数据点的样条插值曲线

4　结　论

本文以四次多项式为基函数构造的1C连续Hermite样条插值曲线，即具有三次样条曲线结构简单易于计算的优点，又提供了额外的自由度用以调整曲线曲面的形状。由于三次B样条几何性质好，且形状上接近插值数据点形成的控制多边形，因此本文利用逼近三次B样条导矢曲线来优化自由度参数，给出了构造可调整的四次Hermite样条插值曲线的显式表达式。实例表明，新方法生成的四次Hermite样条曲线比标准三次Hermite样条曲线更接近插值数据点所建议的形状。

[1] Ahlberg J H, Nilson E N, Walsh J L. The theory of splines and their applications [M]. New York: Academic Press, 1967: 1.

[2] Han X L. A degree by degree recursive construction of Hermite spline interpolants [J]. Journal of Computational and Applied Mathematics, 2009, 225(225): 113-123.

[3] Zhu Y P, Han X L, Han J, et al. Quartic trigonometric Bézier curves and shape preserving interpolation curves [J]. Journal of Computational Information Systems, 2012, 8(2): 905-914.

[4] Mühlbach G. One sided Hermite interpolation by piecew ise different generalized polynomials [J]. Journal of Computational and Applied Mathematics, 2005, 196(1): 285-298.

[5] Agarwal R P, Wong P J Y. Error inequalities in polynomial interpolation and their applications [M]. Dordrecht: Kluwer Academic Publishers, 2012: 217-280.

[6] Kong J H, Jeong S P, Lee S, et al. C1 Hermite interpolation with simple planar PH curves by speed reparametrization [J]. Computer Aided Geometric Design, 2008, 25(4): 214-229.

[7] Goodman T N T, Shape preserving interpolation by curves [C]//Algorithms for Approximation IV. Huddersfield: The University of Huddersfield Press, 2002: 24-35.

[8] 樊敏, 康宝生. 一类Hermite型矢量插值C1细分曲线的几何特征生成[J]. 工程图学学报, 2006, 27(3): 79-83.

[9] Yong J H, Cheng F H. Geometric Hermite curves with minimum strain energy [J]. Computer Aided Geometric Design, 2004, 21(3): 281-301.

[10] Höllig K, Koch J. Geometric Hermite interpolation with maximal order and smoothness [J]. Computer Aided Geometric Design, 1996, 13(8): 681-695.

[11] 张彩明, 汪嘉业. 可调整C2四次Bézier插值曲线的构造[J]. 计算机学报, 2005, 27(12): 1665-1671.

[12] 张彩明, 汪嘉业. C2连续的四次样条曲面插值[J]. 中国科学: E辑, 2003, 33(2): 116-126.

[13] Zhang L, Yang Y, Li Y Y, et al. One fairing method of cubic B-spline curves based on weighted progressive iterative approximation [J]. Computer Aided Drafting Design and Manufacturing, 2014, 25(1): 36-41.

[14] 苏步青, 刘鼎元. 计算几何[M]. 上海: 上海科学技术出版社, 1981: 100-140.

Quartic Herm ite Interpolation Sp line Determ ined by Approximating the Derivative of Cubic B-Sp line Curve

Guo Xiao1, 2,Han Xuli1,Huang Lin2

(1. School of Mathematics and Statistics, Central South University, Changsha Hunan 410083, China; 2. Changsha Normal University, Changsha Hunan 410083, China)

A method is developed to construct adjustable quartic Hermite interpolating spline curves. The extra degree of freedom can be used to adjust the quartic curve to a reasonable shape. The interpolation based on the approximation of derivatives is discussed to make quartic Hermite spline with similar shape feature of cubic B-spline. The degree freedom is determined by minimizing the proximity, which is defined by the squared difference of the derivatives of the curves. The shape of the proposed quartic spline can be adjusted to satisfy the shape-preserving requirement by changing the values of degree of freedom. Four numerical examples are presented to compare the proposed quartic Hermite spline with the standard cubic Herm ite spline.

Hermite interpolating spline; shape-preserving interpolation; shape adjustable

TP 391.72

10.11996/JG.j.2095-302X.2016020149

A

2095-302X(2016)02-0149-06

2015-09-24；定稿日期：2015-10-11

郭啸(1982–)，女，湖南张家界人，讲师，博士研究生。主要研究方向为计算机辅助几何设计。E-mail：guoxiao@csu.edu.cn

韩旭里(1957–)，男，湖南武冈人，教授，博士，博士生导师。主要研究方向为数值逼近、计算机辅助几何设计等。E-mail：xlhan@csu.edu.cn