基于推广B样条细分方法的曲面混合

沈永超， 方美娥

(杭州电子科技大学图形图像研究所，浙江 杭州 310027)

基于推广B样条细分方法的曲面混合

沈永超， 方美娥

(杭州电子科技大学图形图像研究所，浙江 杭州 310027)

提出用推广B样条细分曲面来混合多张曲面的方法，既适用于一般网格曲面，又适用于推广B样条参数曲面混合。根据需要选择阶数和张力参数，可全局调整整张混合曲面的形状。中心点和谷点的计算都设置了形状参数，可局部调整混合部分形状。推导出二次曲面细分初始网格计算公式，并将3阶推广B样条细分曲面混合方法用于多张二次曲面混合，与已有的二次曲面混合方法相比具有明显的优势。

曲面混合；推广B样条细分；控制网格；二次曲面

曲面混合是计算机辅助几何设计领域中曲面造型的常用技术，大量文献对该问题进行了研究[1-7]，多张曲面混合方法包括偏微分方程法(partial differential equation, PDE)、势能方法、隐式曲面方法、参数曲面方法以及细分混合方法等。这些方法有各自的优缺点，但对于多张曲面混合情形，其中大多数方法在混合部分需要多张曲面拼接，可导致各部分曲面不兼容，拼接处的连续性比基曲面低，也不利于混合造型的后续操作，从这个角度看，细分混合方法具有较大优势，混合后的造型是一张整体的细分曲面，不存在拼接问题，且连续性与所选择的细分方法一致，混合效果较好。文献[7]提出的细分混合方法具有代表性，其可用于4×5的曲面片的混合，采用Catmull-Clark细分方法，因此可用于一般网格混合，也可用于基曲面是双三次B样条的情形。本文研究基于推广B样条细分方法(generalized B-spline subdivision, GBS)的多张曲面混合，适用于一般网格混合以及任意次的推广B样条曲面混合，曲面次数的任意性和该方法具有的张力参数可调性也使得混合造型曲面形状调整方便，由于GBS方法可精确生成二次曲面，因此本文方法也可用于二次曲面混合。

1　基于推广B样条的曲面细分方法

GBS方法是一种任意拓扑网格上任意阶带张力参数的非静态细分方法，细分极限曲面在规则网格上为任意次推广B样条曲面(包含经典的B样条曲面、三角多项式空间及双曲多项式空间B样条曲面)，详见文献[8]，这里给出偶数阶和奇数阶的推广B样条细分规则。

1.1偶数阶推广B样条曲面细分

令细分阶数为k，k为偶数，且k≥4，张力参数初值为u0。在细分的第l层，假定当前控制网格为Ml，细分张力参数为ul，则第l层k阶推广B样条曲面细分包括3个步骤：①中点插入；②非均匀光滑；③次均匀光滑。在中点插入步骤中，为网格每条边计算中点，为每个面计算中心点。然后，连接每点中心点和与该面相邻接的中点，并添加到Ml中，形成新的网格，记作Ml+1。在非均匀光滑步骤中，网格的拓扑结构不变，只更新网格顶点。更新顶点的规则为：， VE和Vold是在同一条边上的点，而VF和Vold是在同一个面上的点，取，，且α(N)+β( N)+γ( N)=1，N为相应顶点的邻接边数。在均匀光滑步骤中，网格的拓扑结构同样保持不变，顶点更新规则与非均匀光滑步骤类似，但系数不同，取。另外，每细分一层，细分张力参数按公式迭代更新一次。

1.2奇数阶推广B样条曲面细分(一层)

令细分阶数为k，k为奇数，且k≥3。在细分的第l层，假定当前控制网格为Ml，细分张力参数为u1，则第l层k阶推广B样条曲面细分包括2个步骤：①一次类Chaikin细化；②次均匀光滑。第一步中，计算每个面中每个顶点的新顶点，即，这里是在当前面中位于同一条边上的点，而是当前面中除了Vold和的点，其中取，，拓扑规则与Doo-Sabin细分方法相同。第二步拓扑不变，顶点更新规则与偶数阶算法第三步类似，系数不同，取，。每层细分张力参数按公式迭代更新一次。

2　混合控制网格构造方法

文献[7]针对4×5的网格提出了混合控制网格构造方法，本文为了混合网格适用于任意规模的网格，只提取基曲面2×2的部分网格来构造填补混合部分N边形洞的控制网格，基曲面其余部分网格则采用邻接面连接的方式填充混合网格，其顶点计算公式与提取部分边缘网格顶点相同，因此整个混合部分控制网格构造方法简单。为了避免中心点成为高阶奇异点，采取了中心点向外偏移的办法构造中心多边形网格，避免了中心奇异点的出现。混合网格构造分为4个步骤：辅助点、谷点、中心点计算以及网格拓扑构建。给定基曲面片为N片曲面，记第k片曲面Pk的控制网格为。

2.1计算辅助点

在每个基曲面上提取2×2四边形控制网格，借此构造3行辅助顶点，由于对每个基曲面的操作相同，选取第k个基曲面为例，令其上提取的四边形控制网格的 4个顶点为(在增加辅助点后的网格示意图 1中这 4个点重新编号，分别对应。如图1所示，是和的中点；是和的中点；是和的中点；是的和的平均；是和的中点；是和的中点；是点和的平均；是，，，和的平均；是的和的平均。由此构造的前3行顶点就是构造混合控制网格时要用到的辅助点。

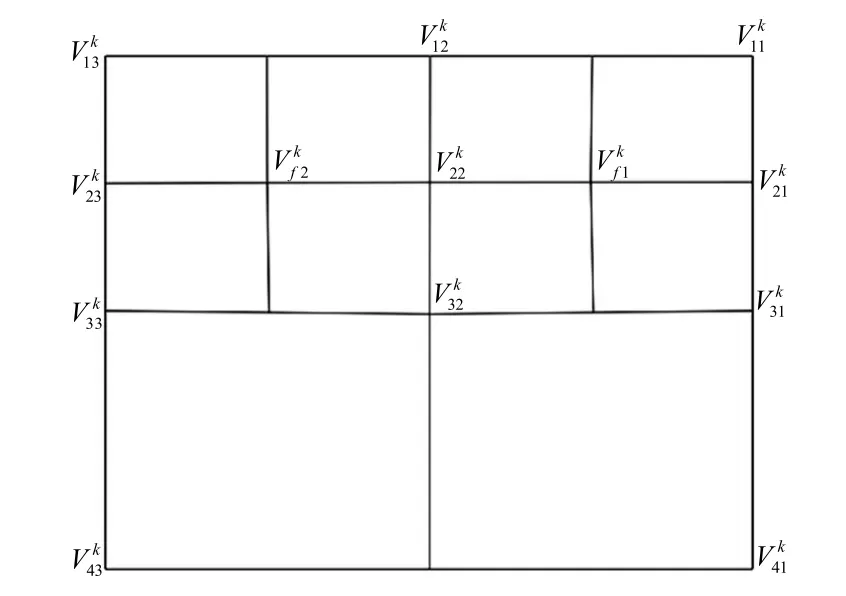
图1　辅助点计算

2.2计算中心点

中心点V0的计算公式如下：

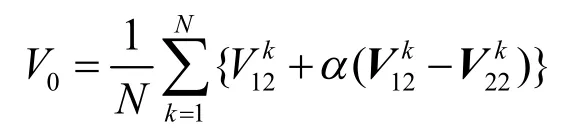
其中，α是可以任意指定的形状控制参数。该公式能使中心点基本位于顶点集的中心，且偏离中心的方向与向量的和同向，由公式可以看出α越大，中心点在向量的和的方向上偏离得就越大。如果直接把V0与各个曲面片的相连，V0的度为N。当N很大时，V0的度就会很大，V0就成为度很高的奇异点。为了避免这种情况，将中心点分别沿的方向上偏移。公式如下：

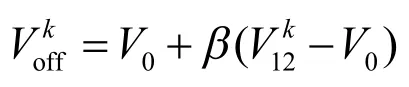
2.3计算谷点

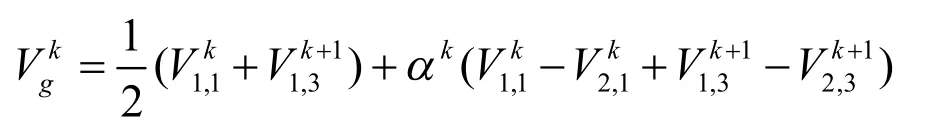
其中，kα是可以任意选择的形状控制参数，kα越大，与的和的方向上的偏移就越大。

2.4混合网格拓扑构建

2.4.1阶为奇数

对 N个曲面片进行如下循环操作：对于第k(1, …, N)个曲面片，将，，依次相连形成一个四边形；将依次相连形成一个三角形；将依次相连形成一个三角形。最后依次连接N个中心偏移点，形成N边形，如图2(a)所示，其中在图中重新编号为，表示第k个谷点的前一个谷点，在图中重新编号为。

2.4.2阶为偶数

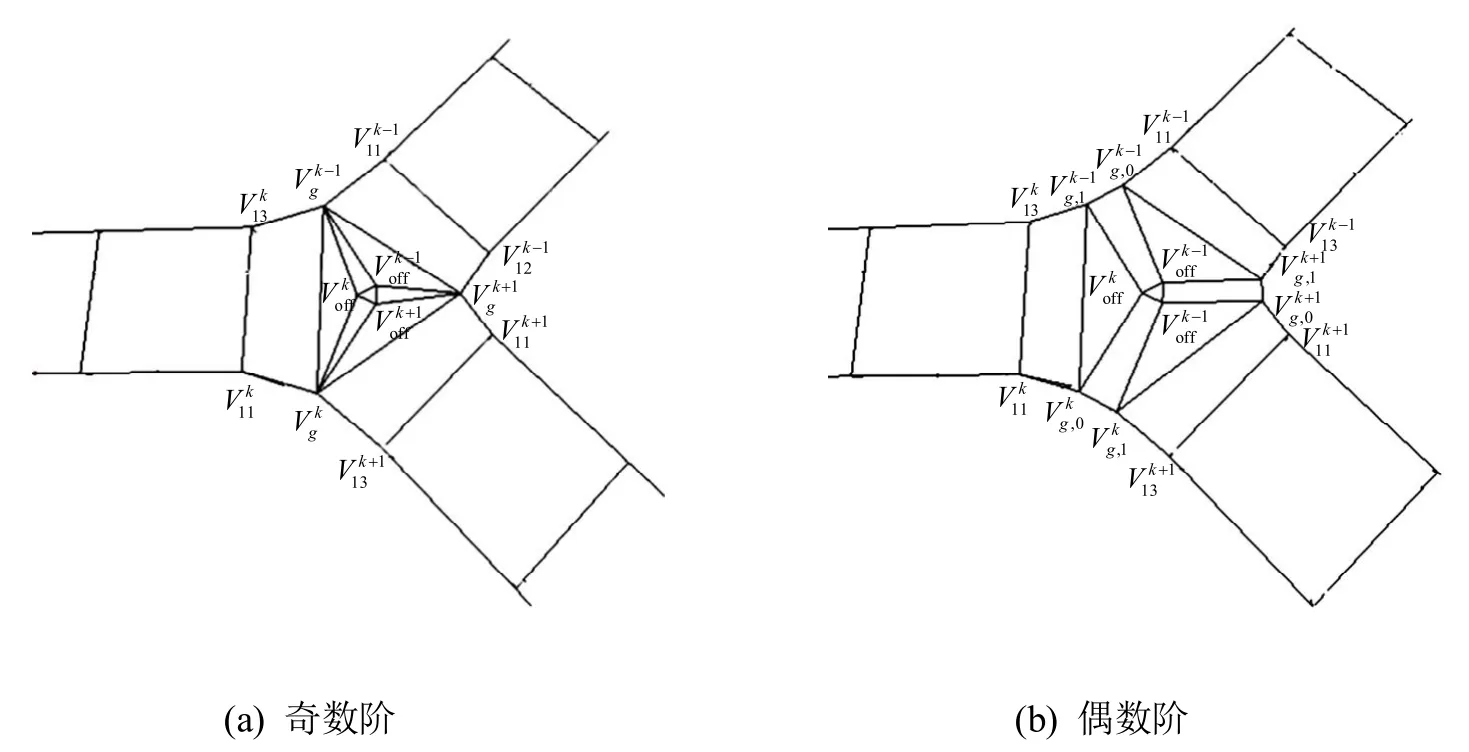
图2　混合网格拓扑构建示意图

图3给出了一个六管道曲面混合的例子。图3(a)是六管道的控制网格，图3(b)是图3(a)混合之后的控制网格。然后用GBS方法对图3(b)混合之后的网格进行细分，图3(c)是设置阶为4，张力参数为2时的结果，图3(d)是阶为8，张力参数为0.7的结果，取不同的阶数和张力参数得到不同形状的混合曲面，可方便地调整混合曲面的形状。混合曲面的光滑性较好，连续性与GBS曲面一致，即采用k阶GBS方法混合则混合曲面整体保持Ck- 2阶连续，只有奇异点处为C1连续，关于GBS曲面的连续性证明见文献[8]。

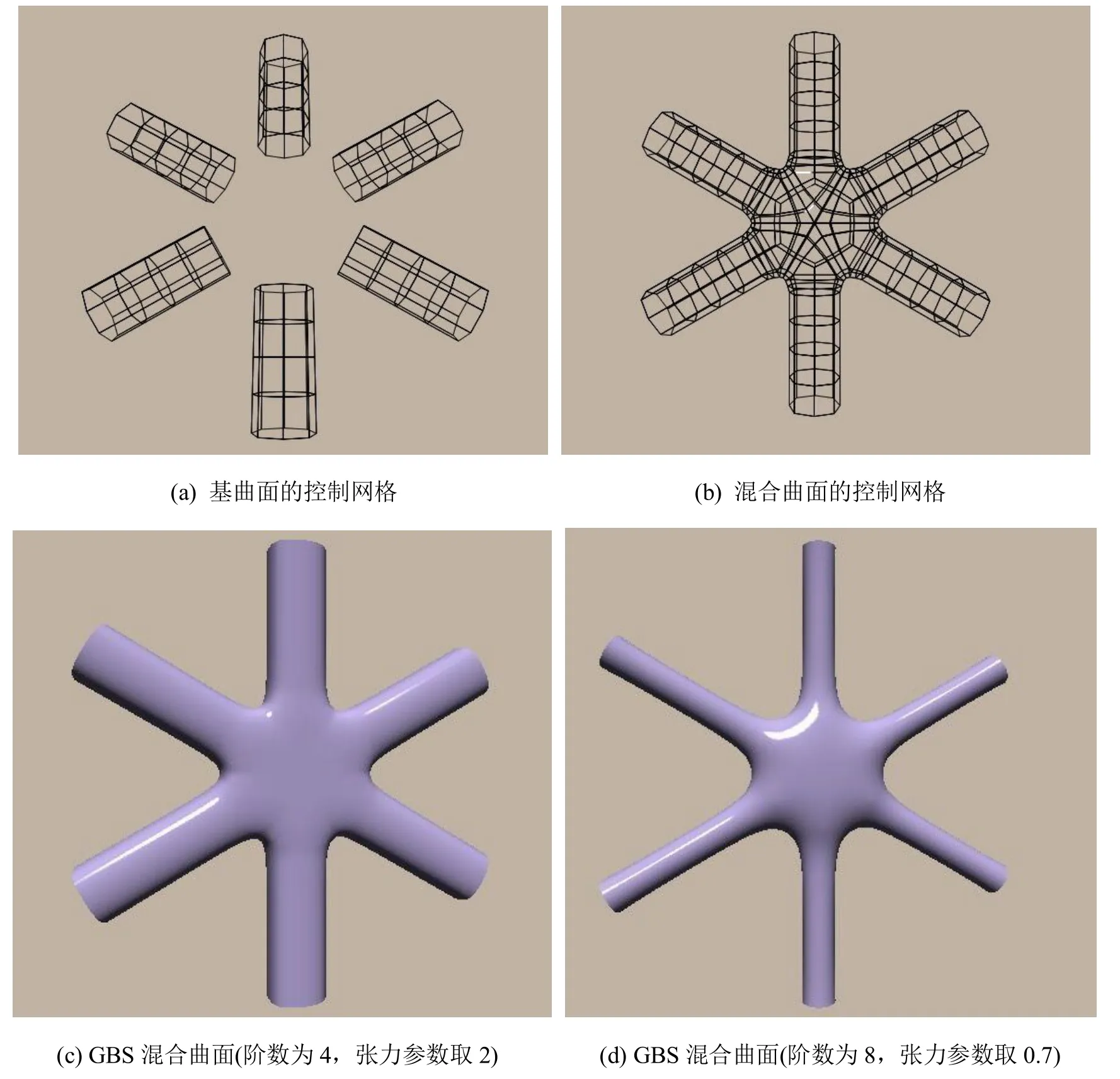
图3　六管道曲面混合

3　基于3阶GBS方法的二次曲面混合

针对多张二次曲面的混合问题也有很多相关研究，如GrÖnder基方法[9]、吴方法[10]、分片代数曲面方法[11]、切分结合S曲面补洞方法等[12]，与一般曲面混合类似，这些方法也存在多张曲面拼接问题，或要求基曲面满足较严格的约束条件，PDE方法及已有的细分混合方法也可用于二次曲面混合，但混合结果只能逼近作为基曲面的二次曲面。由于GBS曲面能精确生成二次曲面，因此运用本文提出的GBS混合方法混合多张二次曲面可以克服已有方法的缺陷，最终的混合曲面为一张细分曲面，方法简单，又具有细分方法的高效性，且不存在拼接问题，由于采用3阶的GBS方法混合二次曲面，因此除个别奇异点外，整张混合曲面保持C1连续。

3阶GBS方法混合二次曲面步骤如下：首先根据基曲面所属二次曲面的类型，计算出精确表示这些基曲面的GBS初始网格，同时确定张力参数，算法详见3.1节，然后运用2.4节的方法构造混合曲面初始网格，再利用3阶GBS方法生成最终的混合曲面。

3.1二次曲面(基曲面)细分初始网格构造

由于二次曲面(圆柱面、抛物面、双曲面、球面、圆锥面)可以看成二次曲线母线(直线、抛物线、双曲线、圆弧、射线)绕其轴线生成的旋转面，因此根据文献[8]旋转曲面的细分初始网格算法，只需要推导出这些二次曲线的3阶推广B样条控制网格即可，然后利用文献[8]的算法2可计算对应二次曲面的细分初始网格。

为公式推导方便，先根据文献[8]对应的推广B样条基函数给出3阶推广B样条基函数及曲线的定义：

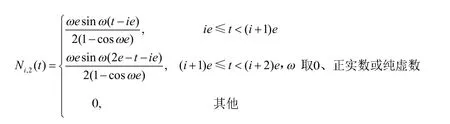
当ω=0时，Ni,2(t)按L’Hospital法则计算。若给定控制顶点序列，则表示以为控制多边形的3阶推广B样条曲线。

下面分别推导3阶推广B样条曲线精确表示抛物线、双曲线和圆弧的控制顶点计算公式，由于GBS是对应细分方法的极限曲线，因此该控制顶点也是3阶推广B样条细分生成的初始网格顶点。

(1) 令抛物线的标准方程为(x(t), y(t))=(t,at2+bt+ c), t∈[t1, t2)，根据ω=0,P( t)=(x(t), y(t))求解可得细分生成该段抛物线的初始网格顶点Pi=(xi, yi)(i=0,1,2)满足：

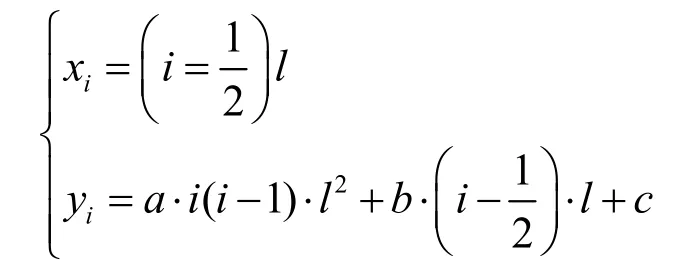
(2) 令双曲线的标准方程为(x( t),y(t)) =(acosh(t), bsinh(t)), t∈[t1, t2)，根据ω=i, P( t)=(x( t), y( t))求解可得细分生成该段抛物线的初始网格顶点Pi( xi, yi)(i=0,1,2)满足：

(3) 令圆弧的标准方程为(x(t),y(t))=(acost , asint), t∈[t1, t2)，根据ω=1,P(t)=(x(t), y(t))求解可得细分生成该段抛物线的初始网格顶点Pi( xi, yi)(i=0,1,2)满足：

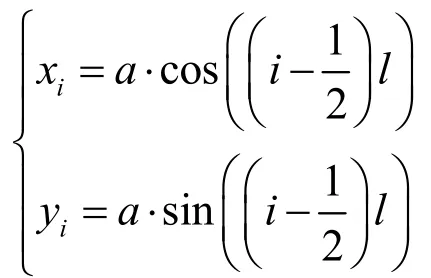
对于一般方程，均可通过坐标变换转换成标准形式，根据标准方程计算出的控制顶点实施相应的逆坐标变换即可获得该曲线的控制顶点。

3.2二次曲面混合实例

给出4个图例来展示用本文的混合方法混合二次曲面的效果，因为基曲面都是二次曲面，均采用3阶的GBS混合方法，张力参数与基曲面一致，其中图4(a)取u0=1，图4(b)、(d)中取 u0=cos(π/4)，图4(c)取 u0=cosh(π/4)。

4　结　论

推广B样条包含了经典的B样条、三角多项式样条和双曲多项式样条，因此基于推广B样条的细分方法在造型上具有适用于任意规模网格、阶数任意、张力参数可调的优势，又能精确地细分生成二次曲面，本文将其应用于一般曲面混合，比已有的细分混合方法造型更丰富，形状调整更方便，应用于二次曲面混合，比已有方法具有面片数少，混合方法简单，效率高等优势。但奇数阶混合网格中存在一些奇异点影响混合效果，未来工作将进一步改进混合部分控制网格构造方法，减少奇异顶点。

图4　二次曲面混合结果

[1] Zhang J J, You L H. PDE based surface representation-vase design [J]. Computers & Graphics 2002, 26(1): 89-98.

[2] You L H, Comninos P, Zhang J J. PDE blending surfaces with C2 continuity [J]. Computers & Graphics, 2004, 28(6): 895-906.

[3] Hartmann E. Blending an implicit with a parametric surface [J]. Computer Aided Geometric Design, 1995, 12(12): 825-835.

[4] Vida J, Matin R R, Varady T. A survey of blending methods that use parametric surfaces [J]. Computer-Aided Design, 1994, 26(5): 341-365.

[5]Liu Y S, Zhang H, Yong J H, et al. Mesh blending [J]. The Visual Computer, 2005, 21(11): 915-927.

[6] Ohbuchi R, Kokojima Y, Takahashi S. Blending shapes by using subdivision surfaces [J]. Computers & Graphics, 2001, 25(1): 41-58.

[7] Li G Q, Li H. Blending parametric patches with subdivision surfaces [J]. Journal of Computer Science and Technology, 2002, 17(4): 498-506.

[8]Fang M E, Ma W Y, Wang G Z. A generalized surface subdivision scheme of arbitrary order with a tension parameter [J]. Computer-Aided Design, 2014, 49(4): 8-17.

[9] Wu T R, Zhou Y S. On blending of several quadratic algebraic surfaces [J]. Computer Aided Geometric Design, 2000, 17(8): 759-766.

[10] Chen F L, Deng J S, Feng Y Y. Algebraic surface blending using Wu’s method [J]. Computer & Mathematics, 2000, (8): 172-181.

[11] Chen C S, Chen F L, Feng Y Y. Blending quadric surfaces with piecew ise algebraic surfaces [J]. Graphical Models, 2001, 63(4): 212-227.

[12] Fang M E, Wang G Z, Ma W Y. N-way blending problem of circular quadrics [J]. Science China Information Sciences, 2010, 53(8): 1546-1554.

Surface Blending Based on Generalized B-Sp line Subdivision

Shen Yongchao,Fang Meie

(Institute of Graphics and Image, Hangzhou Dianzi University, Hangzhou Zhejiang 310027, China)

This article uses generalized B-spline subdivision scheme of arbitrary order with a tension parameter to blend several surfaces, which is suitable to blending both meshes with arbitrary sizes and generalized B-spline control meshes. The shape of blending surfaces can be adjusted globally through changing the order or the tension parameter. Shape parameters are also set during computing central points and valley points. So users can adjust them to locally change the shape of blending section. In addition, we apply the proposed blending method to blend quadrics. The blending results are apparently better than those of existing methods.

surface blending; generalized B-spline subdivision; control meshes; quadrics

TP 391

10.11996/JG.j.2095-302X.2016020172

A

2095-302X(2016)02-0172-06

2015-09-24；定稿日期：2015-11-01

沈永超(1991–)，男，浙江台州人，硕士研究生。主要研究方向为计算机图形学。E-mail：lunnersword@163.com

方美娥(1974–)，女，湖南衡阳人，教授，博士。主要研究方向为计算机辅助几何设计与计算机图形学。E-mail：fme@hdu.edu.cn