无刷直流电动机驱动系统研究
孙丽兵,王金玉,陈国良,潘 杰,张丽莹
(上海太阳能科技有限公司,上海 201108)
无刷直流电动机驱动系统研究
孙丽兵,王金玉,陈国良,潘 杰,张丽莹
(上海太阳能科技有限公司,上海 201108)
系统阐述了无刷直流电动机的基本原理和工作特性,比较分析了无刷直流电动机不同控制策略下的数学模型及拓扑结构。为了分析换相电流及转矩脉动的原理,基于上、下桥臂 PWM调制换相控制方法进行理论及仿真分析,通过仿真验证了所分析方法的正确性和有效性。
无刷直流电动机;驱动电路;转矩波动;换相
0 引 言
无刷直流电动机不仅具有运行效率高、无励磁损耗、控制简单以及调速性能好等特点,又具有结构简单、无需换向器、运行可靠、维护简便等诸多优点,已经在诸多领域中具有广泛应用[1-3],也是目前研究人员比较关注的一种新型电机。无刷直流电动机由电动机主体和驱动器组成,是一种典型的机电一体化产品,它集成了电力电子技术、现代自动控制理论、永磁材料、电机设计、传感器技术、系统电路等不同领域为一体,是现代控制领域新技术的综合体[4-9]。
本文分析了无刷直流电动机不同控制策略下的数学模型及拓扑结构,并详细地分析了驱动系统PWM调制原理,通过PSIM电力电子仿真软件进行相应仿真,仿真结果验证了理论分析的正确性。
1 无刷直流电动机数学模型及驱动电路拓扑
无刷直流电动机采用三相变量数学模型,绕组三相对称,忽略涡流损耗和磁滞损耗,不考虑电机的齿槽效应和铁心磁路饱和的影响,气隙磁场分布近似梯形波。根据以上假设,相绕组电压方程可表示:
(1)
式中:ua,ub,uc为相电压;R为相绕组电阻;ia,ib,ic为相电流;ψa,ψb,ψc为每相绕组总磁链。
式(1)中,每相绕组总磁链表达式:
(2)
式中:L为定子相绕组自感;M为定子相绕组互感;ψar,ψbr,ψcr分别为转子永磁体在a相,b相,c相绕组产生的磁链。
由于定子绕组对称,因此定子电流满足:
(3)
将式(3)代入式(2)得:
(4)
将式(4)代入式(1)得:
(5)
令:
(6)
式中:ea,eb,ec分别为定子a相,b相,c相反电势;Ls为电机漏感。
将式(6)代入式(5),得:
(7)
电机端电压数学模型:
(8)
式中:ua0,ub0,uc0分别为定子a相,b相,c相绕组对功率地电压;un为电机中性点对功率地电压。
电机输出的电磁功率:
(9)
无刷直流电动机的电磁转矩:
(10)
式中:ωr为转子机械角速度。
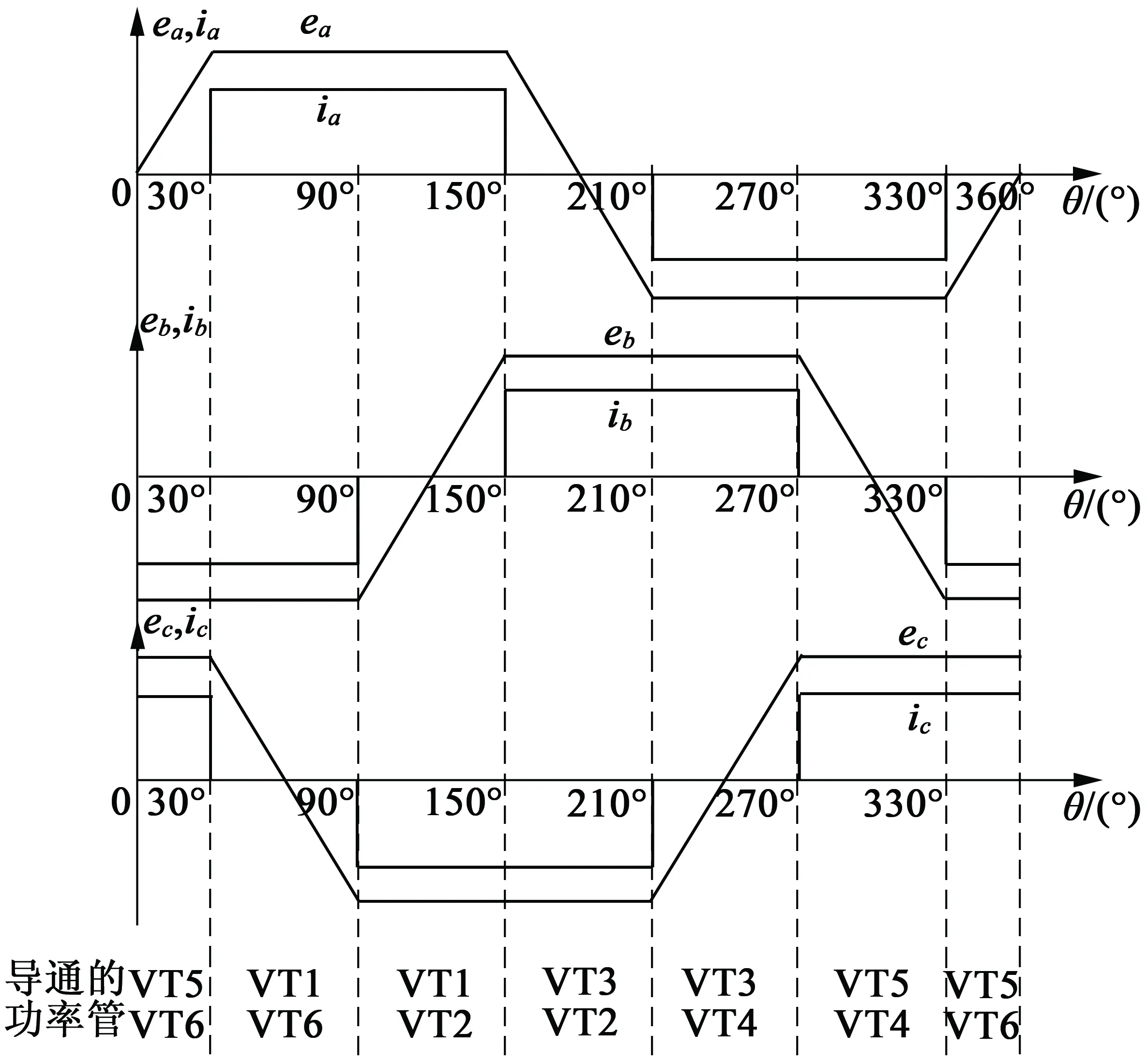
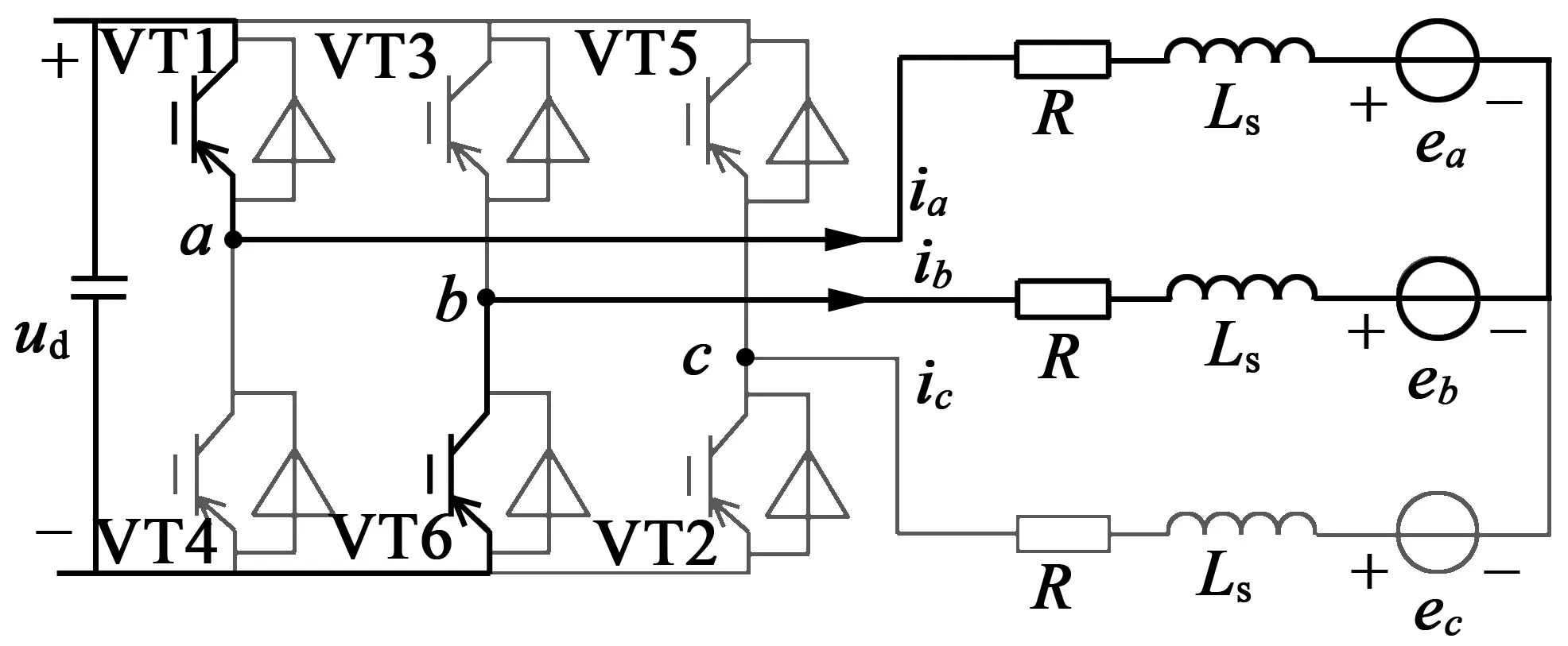
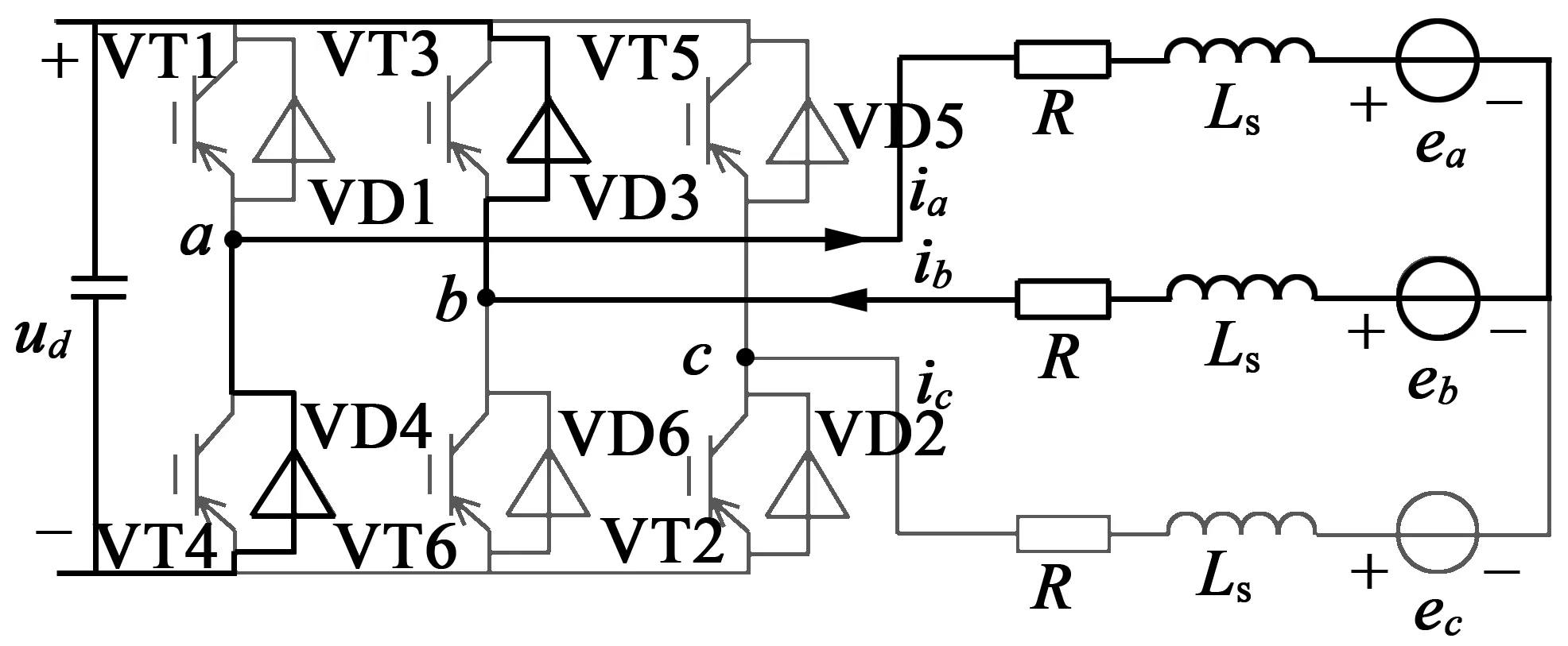
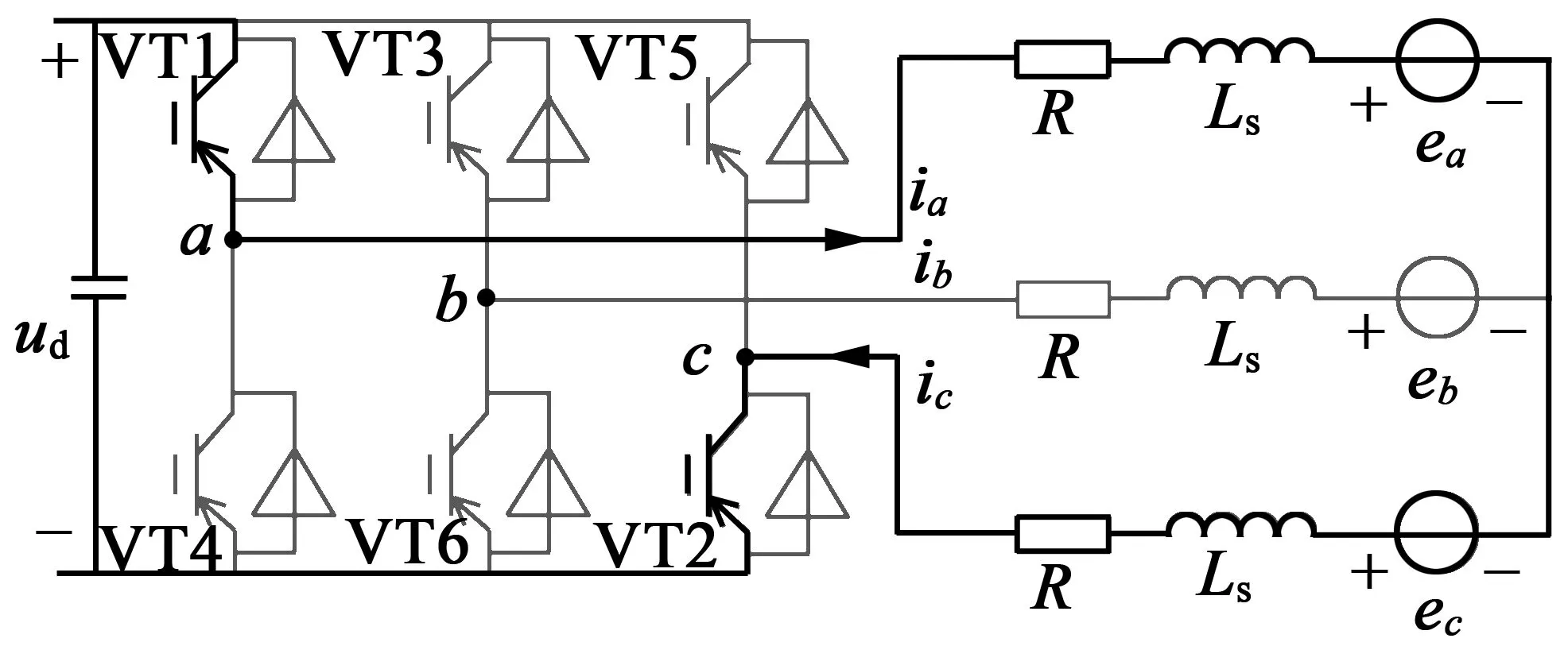
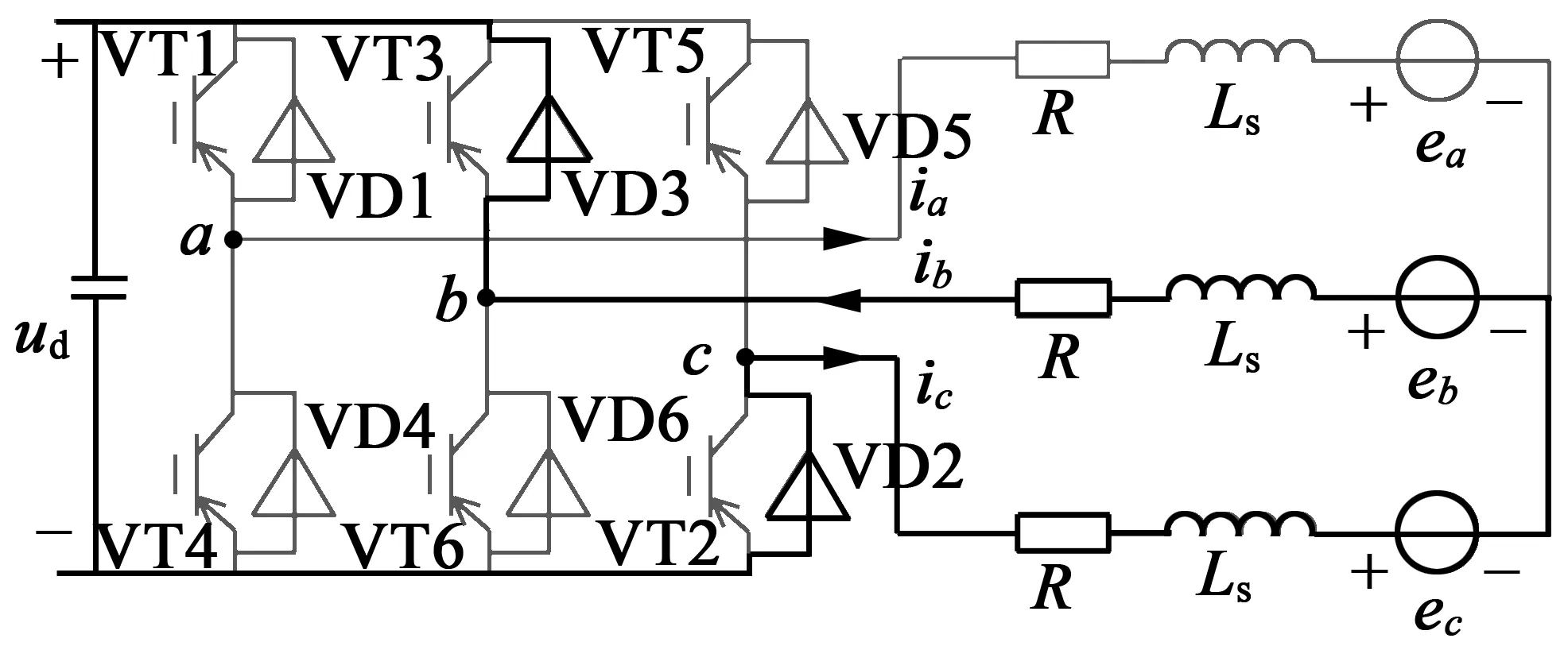
图1为无刷直流电动机驱动电路拓扑原理图,图 2为无刷直流电动机理想的反电动势、电流波形与功率器件导通关系图。为了产生最大的恒电磁转矩,转子永磁体产生的励磁磁场与定子绕组电枢磁场成正交状态,永磁体产生的磁链ψa,ψb,ψc要与电流ia,ib,ic产生的磁链正交,而永磁体磁链ψa,ψb,ψc求偏导得到感应反电势ea,eb,ec,所以ea,eb,ec波形与ia,ib,ic波形在稳定阶段角度重合。在相与相之间的切换中,感应反电势ea,eb,ec会线性上升或下降。
无刷直流电动机与普通有刷直流电动机在运行方式及性能方面有一定的差别。在实际运行过程中,普通有刷直流电动机励磁磁场与电枢磁场为正交状态,无刷直流电动机永磁励磁磁场与电枢磁场在60°~120°范围内变化,90°正交状态为其间的一个瞬时位置。因此,有刷直流电动机存在换相过程,存在一定的转矩脉动,在相同的工况下,其转矩脉动幅值要大于有刷直流电动机。
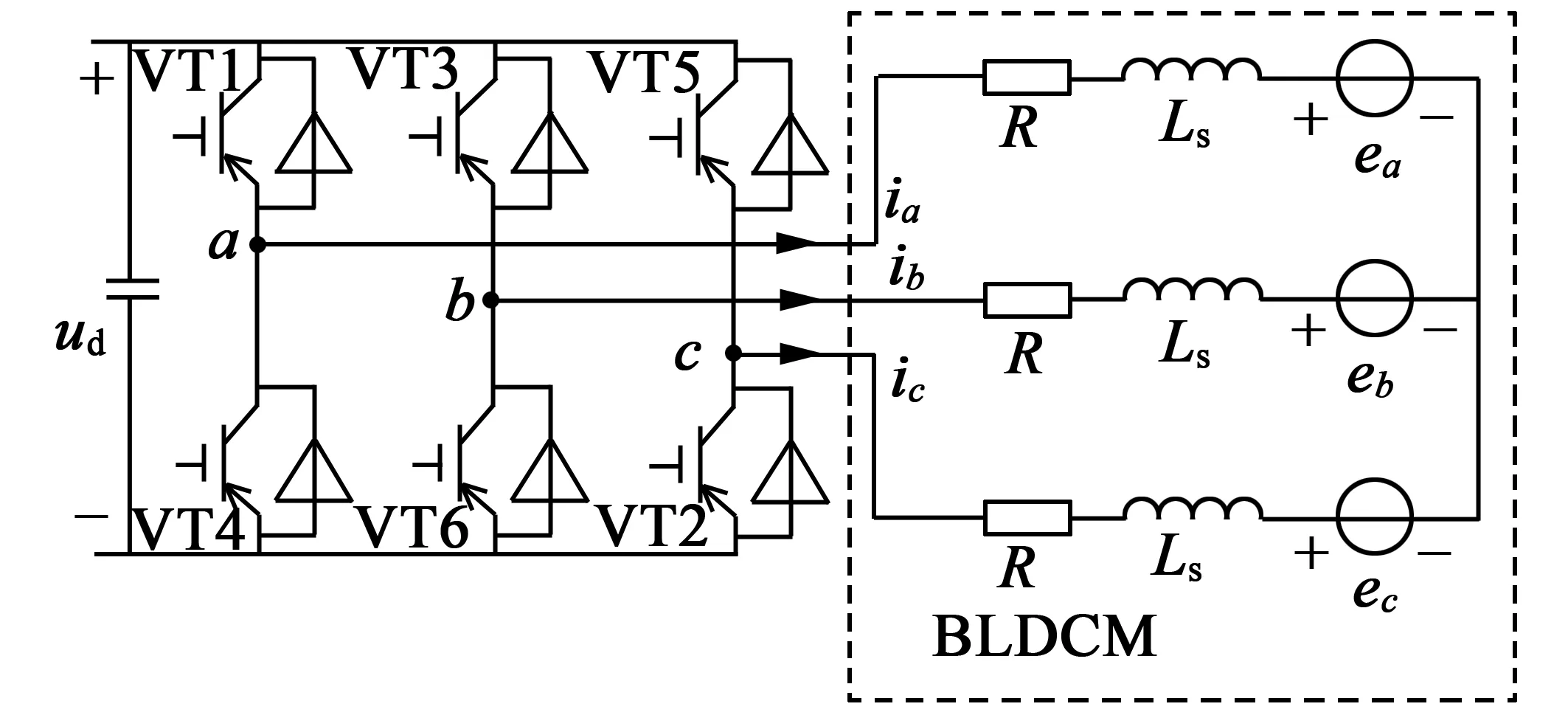
图1 无刷直流电动机驱动电路拓扑原理图
(a)

(b)
2 无刷直流电动机控制策略
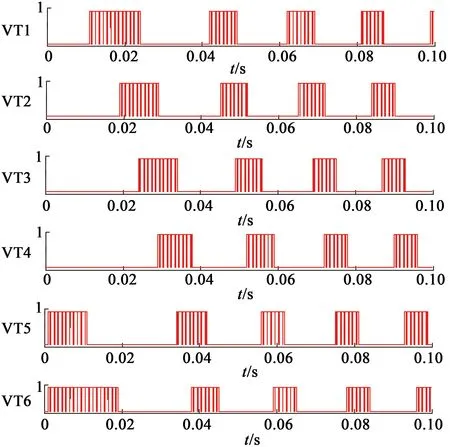
无刷直流电动机控制系统包含全压控制和PWM调制控制方式。全压控制为每60°切换一次开关状态,在60°范围内,器件开关状态保持不变,原理图如图 2 (b)所示,这种方式当直流母线电压恒定不变时,无刷直流电动机电磁转矩不能改变,要更改输出转矩只能调节直流母线电压。为了在直流母线电压不变的情况下,对电磁转矩进行调节,通常采用PWM调制方式,即在非开关状态切换的60°范围内采用PWM调制,即输出一定比例的占空比。PWM调制控制方式包含不同的调制策略,可以根据上桥臂、下桥臂为PWM调制还是恒通模式进行分类。为了分析换相电流及转矩脉动的原理,基于上、下桥臂PWM调制换相控制方法进行理论及仿真分析,通过仿真验证了所分析方法的正确性和有效性。对于其它不同的PWM调制方式原理相同,就不分别进行仿真分析。
与全压控制不同,采用PWM调制是为了在直流母线电压恒定的情况下可以调节输出电流即输出电磁转矩,图 3为器件开关状态示意图及仿真波形,图 4为电机转速、三相电流、相电压、线电压仿真波形,下面分别对一个周期十二种开关状态分别进行分析,每60°分成一个区间。

(a)
(b)
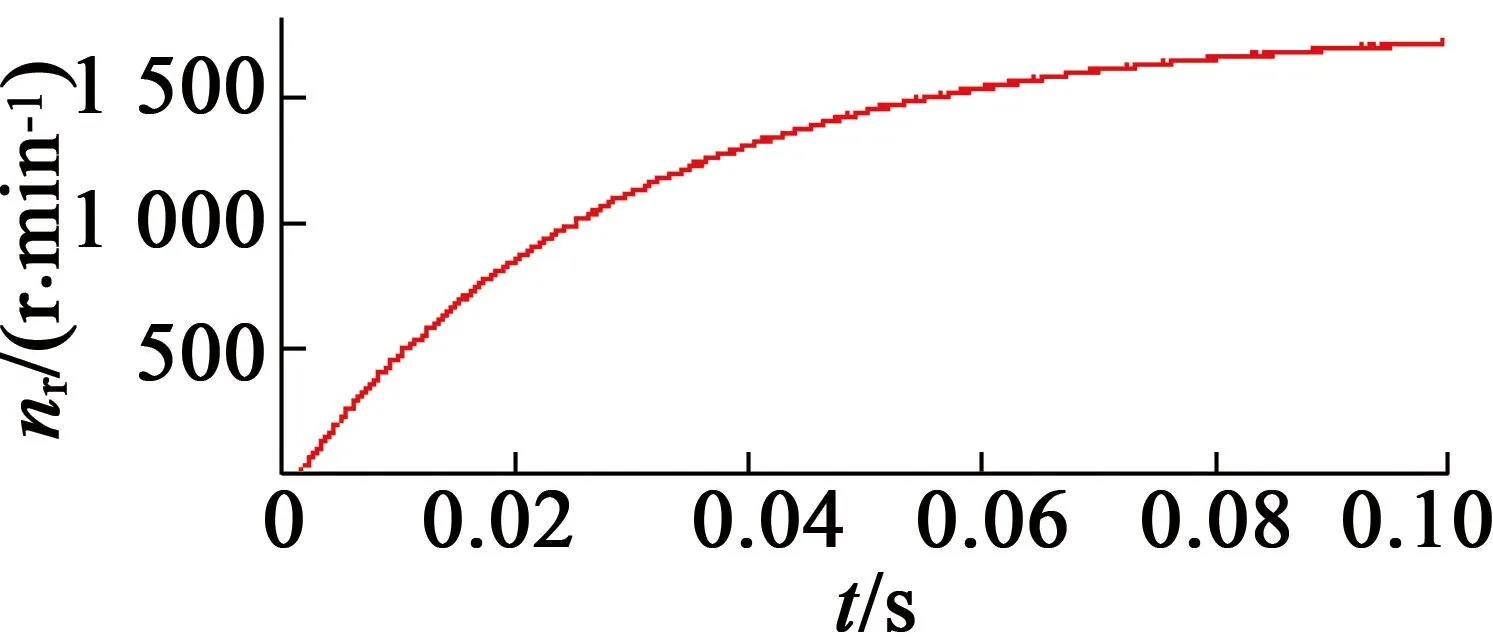
(a) 转速

(b) 三相电流

(c) 相电压
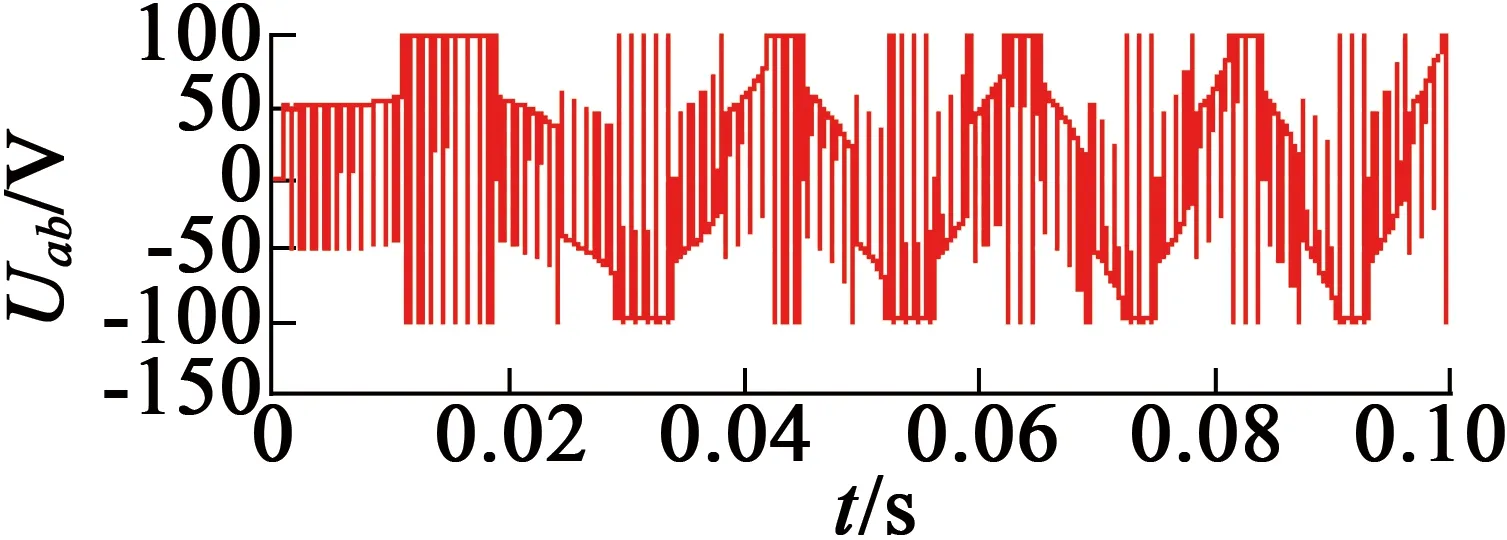
(d) 线电压
(1)[0°,60°]——VT6,VT1开通或VT6,VT1关断
这个区间存在两种开关状态,即功率管VT6,VT1同时开通,功率管VT6,VT1同时关断。功率管VT6,VT1同时导通,电流回路如图 5(a)所示,该状态下电路方程:
(11)
此时,电路中存在ua=Ud,ub=0,将式(11)前两式相加,可以求得电机中性点对功率地电压un:
(12)
非导通相C相电压uc:
(13)
功率管VT6,VT1同时关断,电流回路如图 5(b)所示。基于电机电感续流作用,A,B相绕组的电流ia,ib不能立即消失,通过反向二极管D3,D4 续流,该状态下电路方程:
(14)
此时,电路中存在ua=0,ub=Ud,将式(14)前两式相加可以求得电机中性点对功率地电压un:
(15)
非导通相C相电压uc:
(16)
反向二极管VD3,VD4续流工况下的电机中性点对功率地电压un、非导通相C相电压uc表达式与功率管VT6,VT1同时开通相同。图 6为开关器件VT6,VT1、三相电流、电机中性点对功率地电压un、相电压uc的仿真波形,PWM占空比为70%,在开关器件切换时刻存在电压、电流的波动。
(a) 功率管VT6,VT1同时开通
(b) 功率管VT6,VT1同时关断
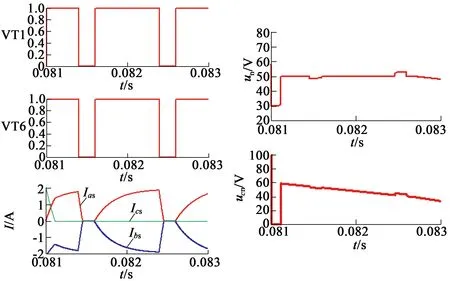
图6 [0°,60°]电压、电流仿真波形
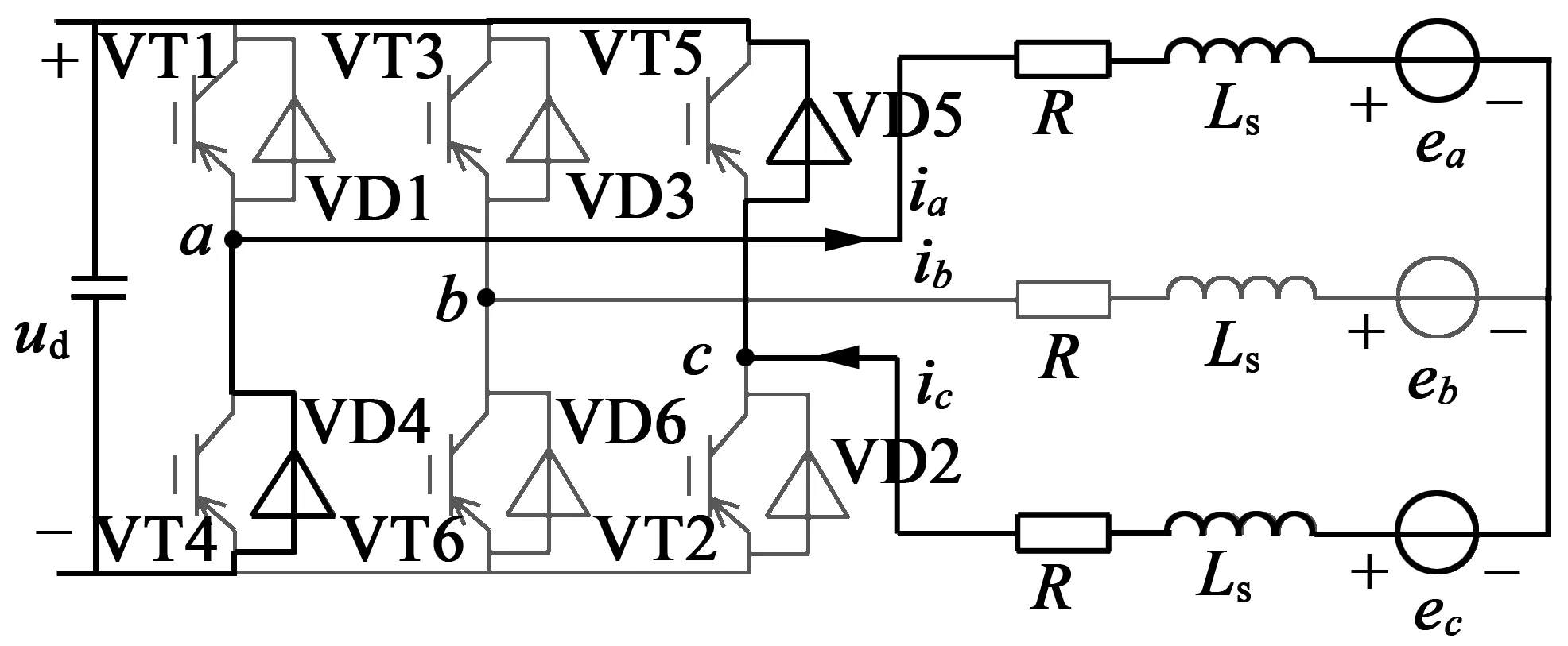
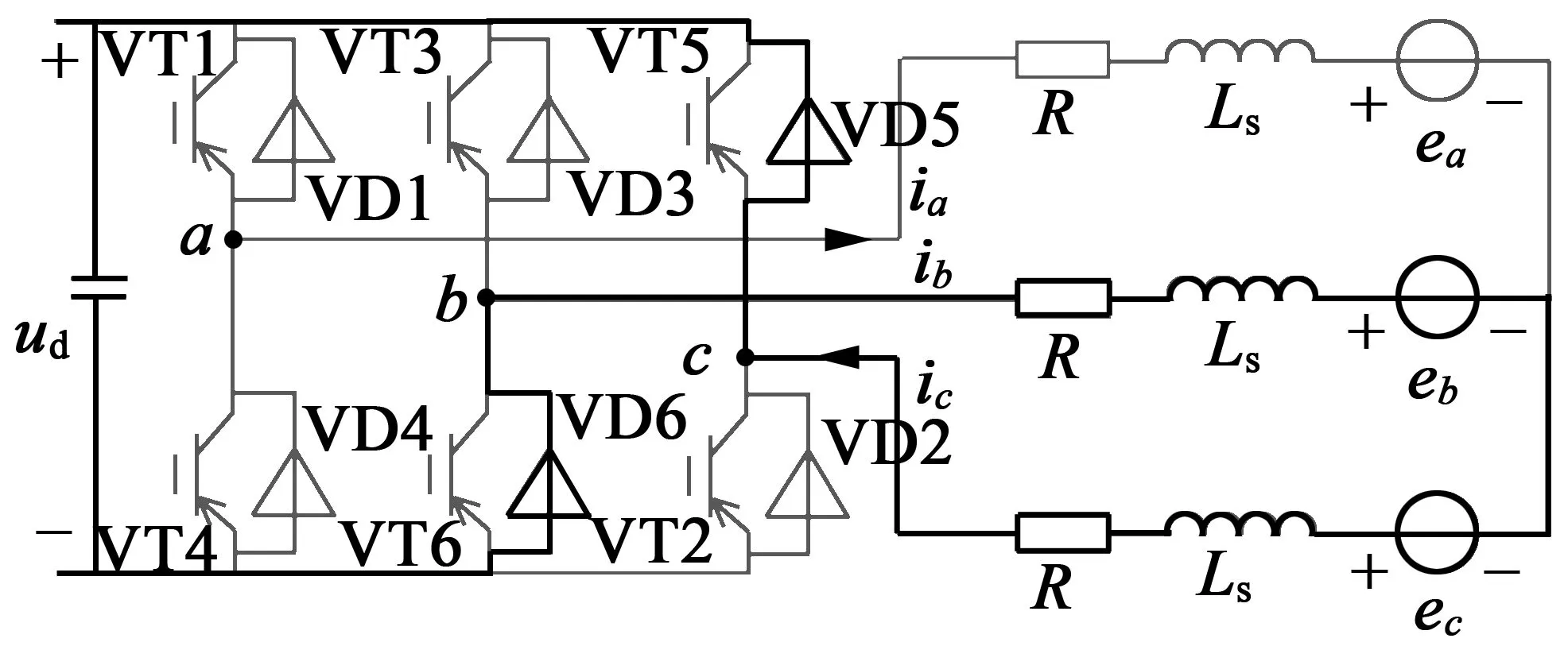
(2)[60°,120°]——VT1,VT2开通或VT1,VT2关断
这个区间存在两种开关状态,即功率管VT1,VT2同时开通,功率管VT1,VT2同时关断。电流回路如图 7所示。图 8为开关器件VT1,VT2、三相电流、电机中性点对功率地电压un、相电压ub的仿真波形,PWM占空比为70%,在开关器件切换时刻存在电压、电流的波动。
(a) 功率管VT1,VT2同时开通
(b) 功率管VT1,VT2同时关断

图8 [60°,120°]电压、电流仿真波形
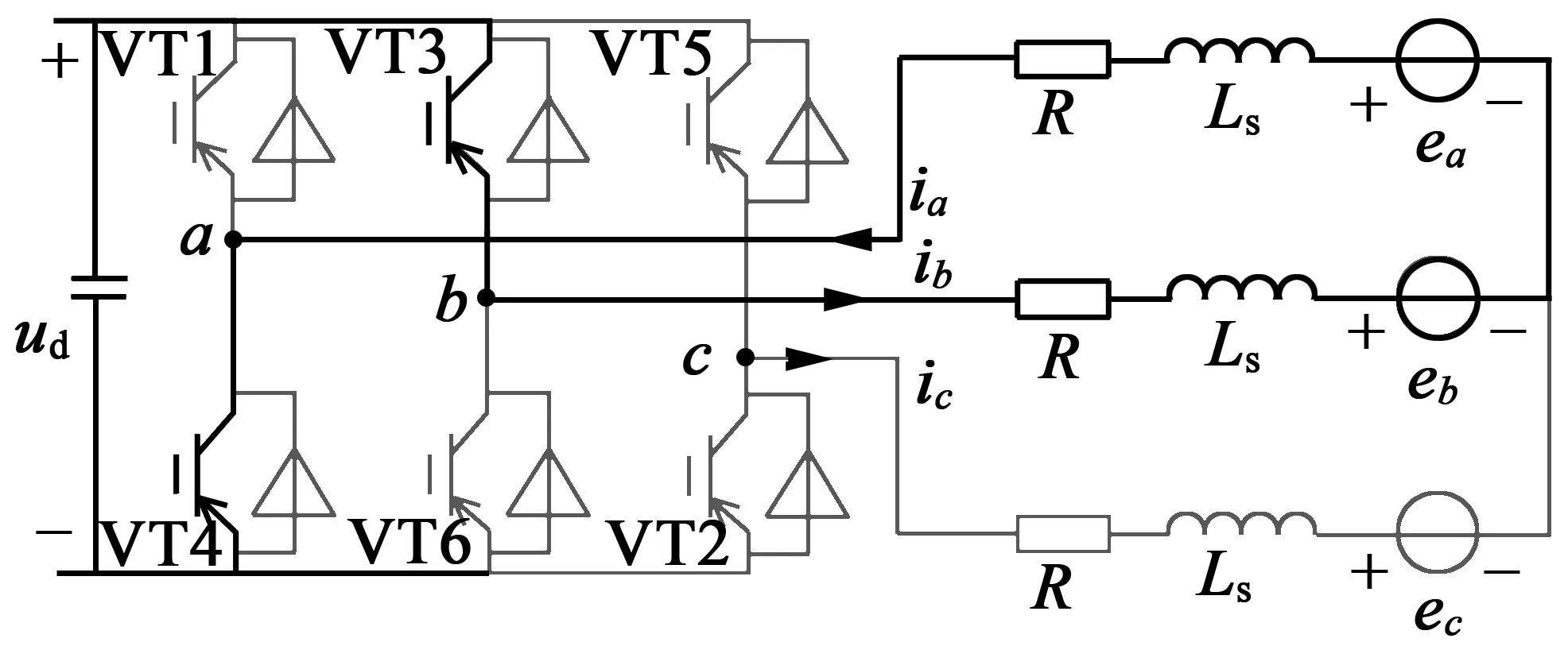
(3)[120°,180°]——VT2,VT3开通或VT2,VT3关断
这个区间存在两种开关状态,即功率管VT2,VT3同时开通,功率管VT2,VT3同时关断。电流回路如图 9所示。图 10为开关器件VT2,VT3、三相电流、电机中性点对功率地电压un、相电压ua的仿真波形,PWM占空比为70%,在开关器件切换时刻存在电压、电流的波动。

(a) 功率管VT2、VT3同时开通
(b) 功率管VT2、VT3同时关断

图10 [120°,180°]电压、电流仿真波形
(4)[180°,240°]——VT3,VT4开通或VT3,VT4关断
这个区间存在两种开关状态,即功率管VT3,VT4同时开通,功率管VT3,VT4同时关断。电流回路如图 11所示。图 12为开关器件VT3,VT4、三相电流、电机中性点对功率地电压un、相电压uc的仿真波形,PWM占空比为70%,在开关器件切换时刻存在电压、电流的波动。
(a) 功率管VT2,VT3同时开通
(b) 功率管VT3,VT4同时关断
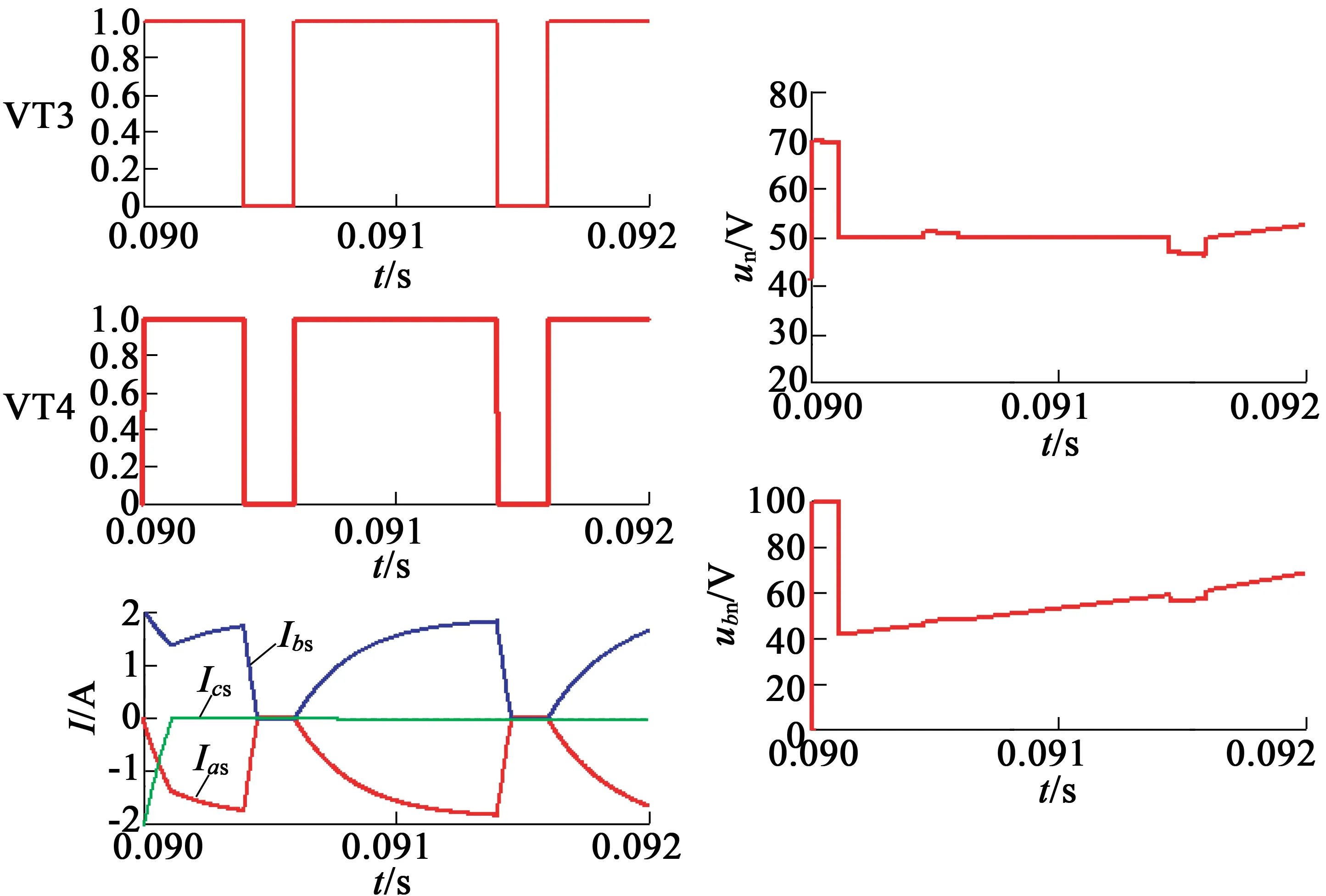
图12 [180°,240°]电压、电流仿真波形
(5)[240°,300°]——VT4,VT5开通或VT4,VT5关断
这个区间存在两种开关状态,即功率管VT4,VT5同时开通,功率管VT4,VT5同时关断,电流回路如图 13所示。图 14为开关器件VT4,VT5、三相电流、电机中性点对功率地电压un、相电压ub的仿真波形,PWM占空比为70%,在开关器件切换时刻存在电压、电流的波动。
(a) 功率管VT4,VT5同时开通

(b) 功率管VT4,VT5同时关断
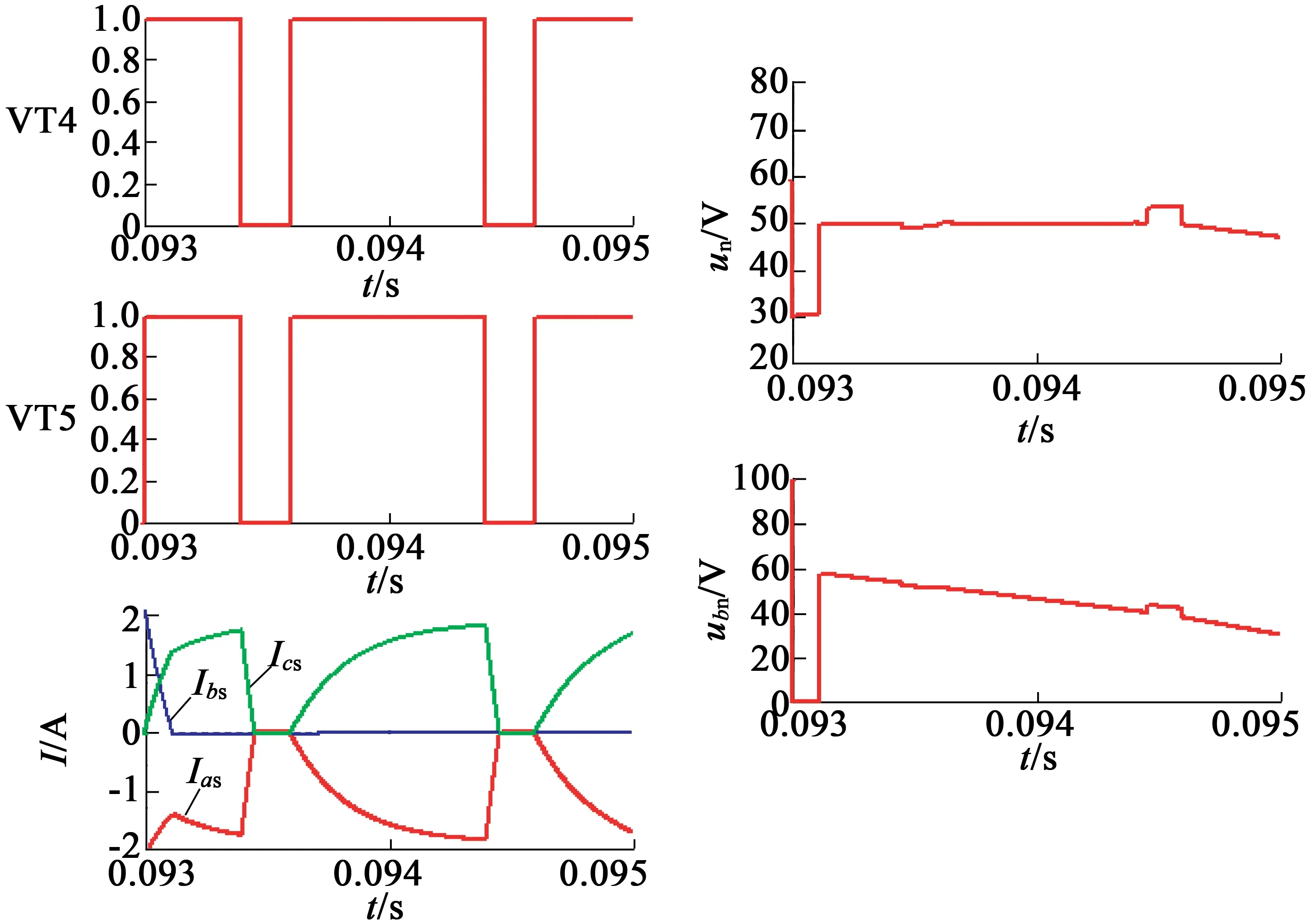
图14 [240°,300°]电压、电流仿真波形
(6)[300°,360°]——VT5,VT6开通或VT5,VT6关断
这个区间存在两种开关状态,即功率管VT5,VT6同时开通,功率管VT5,VT6同时关断。电流回路如图 15所示。图 16为开关器件VT5,VT6、三相电流、电机中性点对功率地电压un、相电压ua的仿真波形,PWM占空比为70%,在开关器件切换时刻存在电压、电流的波动。

(a) 功率管VT5,VT6同时开通
(b) 功率管VT5,VT6同时关断

图16 [300°,360°]电压、电流仿真波形
3 结 语
本文对无刷直流电动机的数学模型进行了详细分析,分析了器件在不同开关状态下的电流回路及方程表达式,研究了无刷直流电动机换相产生转矩脉动的原因,对全压控制和 PWM 调制控制原理进行了对比分析,并以上、下桥臂 PWM调制为例进行一个周期开关状态、电路回路分析及仿真,经过仿真验证,采用PWM调制将会减小电流及换相转矩脉动,增加电机运行的稳定性。
[1] 王迎发.无刷直流电机换相转矩波动抑制与无位置传感器控制研究 [D].天津:天津大学,2011.
[2] CARLSON R,LAJOIE M M,FAGUNDES J C.Analysis of torque ripple due to phase commutation in brushless DC machines [J]. IEEE Transactions on Industry Applications, 1992, 28(3): 632-638.
[3] LAI Y-S,LIN Y-K.Novel back-EMF detection technique of brushless DC motor drives for wide range control without using current and position sensors[J].IEEE Transactions on Power Electronics,2008,23(2):934-940.
[4] 王大方,卜德明,朱成,等.一种减小无刷直流电机换相转矩脉动的调制方法[J].电工技术学报,2014,29(5): 160-166.
[5] 夏长亮,方红伟.永磁无刷直流电机及其控制[J].电工技术学报,2012,27(3): 25-34.
[6] 张磊,瞿文龙,陆海峰,等.一种新颖的无刷直流电机无位置传感器控制系统[J].电工技术学报,2006,21(10): 26-30.
[7] 李自成,程善美,蔡凯,等.反电动势过零检测无刷直流电机转子位置新方法[J].电工技术学报,2009,24(7): 52-58.
[8] 罗宏浩,吴峻,赵宏涛,等.永磁无刷直流电机换相控制研究[J].中国电机工程学报,2008,28(24): 108-112.
[9] 史婷娜,吴曙光,方攸同,等.无位置传感器永磁无刷直流电机的起动控制研究[J].中国电机工程学报,2009,29(6): 111-116.
Simulation of Brushless DC Motor Drive System
SUN Li-bin, WANG Jin-yu, CHEN Guo-liang, PAN Jie, ZHANG Li-ying
(Shanghai Solar Energy S&T Co., Ltd.,Shanghai 100190,China)
The basic principles and operating characteristics of the permanent-magnet brushless DC motor were described, and a comparative analysis of the mathematical model and the topology under different control strategies was given. In order to analyze the principles of commutation current and torque ripple, control theory and simulation analysis based on the upper and lower arm PWM modulation commutation method were adopted. The simulation results show the correctness and validity of the commutation control method.
brushless DC motors; driving circuit; torque ripple; commutation
2015-10-09
国家国际科技合作专项项目(2014DFG62610)
TM33
A
1004-7018(2016)03-0065-06
孙丽兵(1982-),男,研究方向为电力电子与电气传动、微电网系统设计。

