基于无源性异步电动机无速度传感器的调速研究

王腾飞，张 斌

(兰州交通大学，兰州 730070)



基于无源性异步电动机无速度传感器的调速研究

王腾飞，张 斌

(兰州交通大学，兰州 730070)

针对交流异步电动机非线性、强耦合、大干扰等问题，采用无源性理论从能量交换的观点分析电机控制系统，从模型中分离出无功力，简化了控制器的设计，通过能量成型和阻尼注入等方法，推导出了全局稳定的非线性动态反馈控制率，同时为了避免传统机械速度传感器带来的麻烦，结合运用模型参考自适应的无速度传感器控制方法，进行MATLAB仿真，并与有速度传感器情况下进行对比，分析说明了异步电动机无源性调速在无速度传感器情况下的可行性和有效性。

异步电动机；无速度传感器；模型参考自适应控制；无源性

0 引 言

交流异步电动机是经典的非线性、耦合度高、干扰因素多的复杂控制对象，为了得到更好的动、静态性能及抗干扰性能，其控制策略吸引了众多中外学者深入研究，其中主要的非线性方法[1-2]有：反馈线性化方法、积分反步法、无源理论控制方法、滑模变结构法等。无源控制法是Romeo Ortega等外国学者在机器人自动控制研究中引发出的[3]。其定义为假如受控对象的能量不大于其内部初始能量与外界注入能量的和，即说明该受控对象总是吸入外界的能量，而不向外放出能量，即可称为无源的。无源性理论是研究受控对象内外部之间能量交换及耗散的方法，其基本设计步骤：重新分配受控系统的能量特性方程，从中分离出不影响能量变化的无功力分量，从而使得受控系统总能量渐近趋于预设的能量函数方程，故其中的状态变量也相应地趋于期望目标变化[4-5]。比较多种非线性的理论方法，运用无源性观点建立系统的控制器无奇异点问题，系统能达到全局稳定的状态，对时变的参数和外界的干扰鲁棒性较强。

本文基于无源性交流异步电动机调速系统，针对无速度传感器的情况运用模型参考自适应的原理设计了转速估算环节，通过与有速度传感器件时对比，说明了异步电动机无源性调速无速度传感器的可行性及良好的调速性能。

1 异步电动机的数学模型

据电机学可知，在两相旋转d,q坐标系中交流异步电动机的数学模型可分为电气和机械两个子系统，其中电气子系统电压磁链方程：

(1)

机械子系统运动方程：

(2)

(3)

可以认为，式(3)左侧第一项为作用力，第二项为无功分量，第三项是耗散力，第四项为外部扰动。其中：

式(3)两边同乘以xT可,得：

(4)

因C(ω1,x)具有反对称性，则不影响系统能量的变化，也不会对系统稳定性造成影响，所以在异步电动机控制系统设计中无需考虑这项变量因素。这一过程可称为配置无功分量[6]。

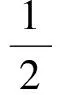
(5)

对式(5)两边积分可得:

可以看出左侧为机械部分t时刻能量的变化量，右侧为t时刻供给机械部分的总能量，则根据无源性理论其机械系统部分为无源的。

由以上分析知,异步电动机两个子系统都是无源的，则可说明整个系统模型严格的无源。故其系统能表示成子系统模型负反馈并联的方式[7]。如图1所示,电气子系统:

机械子系统:

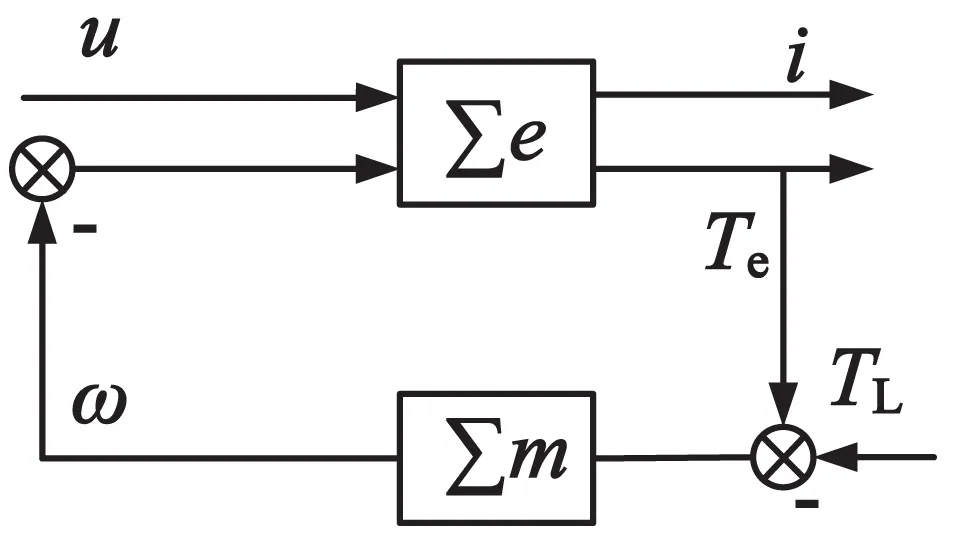
图1 异步电动机子系统负反馈并联结构图

经过分析，将机械部分当作系统无源干扰，而将电气部分当作受控对象，故减少了设计难度，使控制器变得简单。

2 速度传感器

2.1 有速度传感器

交流电机的调速系统必须实时掌握转速信息，才能实现闭环电机转速的控制，且检测信号是否精确,将直接对磁场定向造成影响。闭环反馈到控制器的转速信号直接来源于速度传感器件的情况即称有速度传感器。图2为基于无源性设计的异步电动机调速系统在有传感器件情况下的结构图。

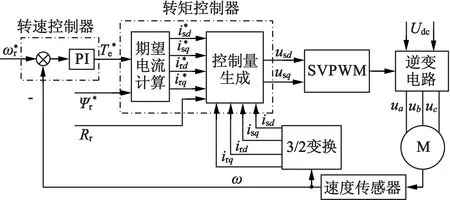
图2 无源性控制异步电动机调速的结构框图

2.2 无速度传感器

速度传感器件的使用会带来一些弊端，比如安装过程中容易出现机械偏差、成本较高、维护不便等。因此无传感器件的电机调速成为了交流调速系统中的热点方向，一方面减少了设备，使得系统的体积小、重量轻：另一方面也避免了速度传感器本身的不足，提高了可靠性，减少了安装成本。

转速估算常用的方法[8]有很多，主要有自适应的PI控制法、转速动态估测法、模型参考自适应法、EKF方法等。本文采用模型参考自适应(MRAC)的原理进行速度估算[9]，并通过仿真观察估算效果。

MRAC速度估算的原理是计算两个具有相同输出的模型之间差值，求得相应的自适应控制律以修正变化的参数值，达到输出逼近参考值的效果。待估参数只存在于可调模型中，而参考模型不含。

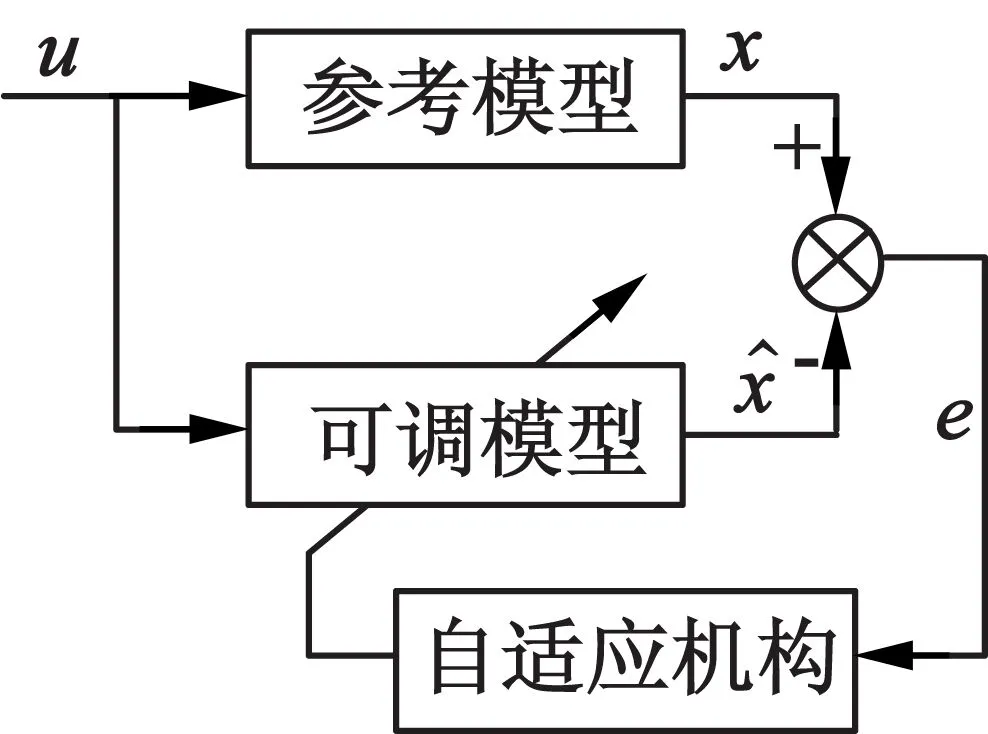
图3 MRAC原理框图

(1)基于磁链的MRAC模型

因计算ωr的电压方程式中不含转速，将其输出作为期望值，电流方程包含转速，将其输出作为估算值，根据表达式算出转速:

式中：ψrd1,ψrq1由电压方程算得；ψrd2,ψrq2由电流方程算得。

(2)基于无功功率的MRAC模型

以电机无功功率的MRAC模型方法解决了磁链计算中受定子电阻影响大的不足，减小估算误差。定义瞬时无功功率：

Q=isus

以us和is表示的无功功率：

(6)

以ψr和is表示的无功功率：

(7)

由于式(6)不含转速信号，用来作参考模型；式(7)含转速信号，用来做可调模型。因此基于无功功率的MRAC模型可表示：

综上所述，加入MRAC的无源性异步电动机调速系统框图如图4表示。

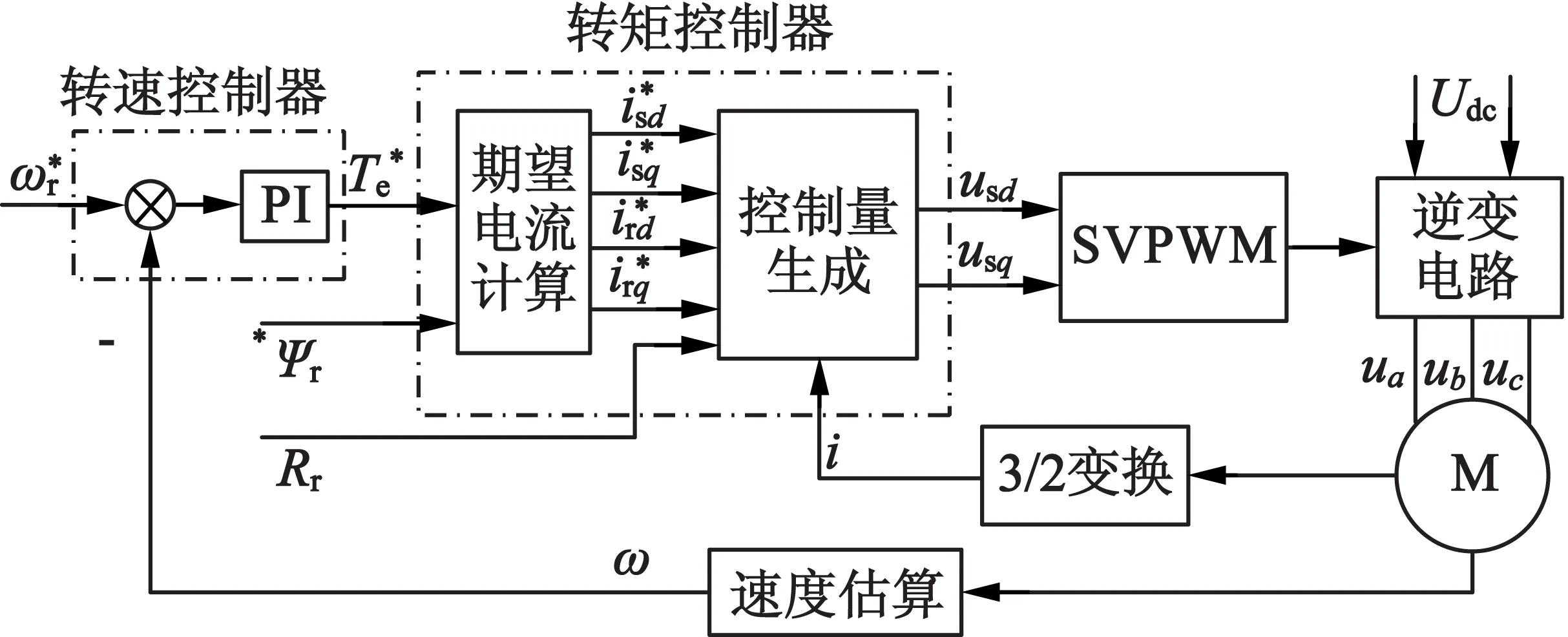
图4 无源性控制异步电动机的无传感器系统结构图

3 无源控制器的设计

3.1 转矩控制器

(8)

异步电动机的调速控制目标[10]：

电磁转矩收敛到期望值：

(9)

转子磁场渐近定向：

(10)

磁链的幅值逐渐趋于给定：

(11)

(12)

取式(12)的能量储存函数：

(13)

对其进行时间求导,得：

(14)

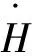
根据控制目标，由式(9)～式(11)可得：

(15)

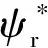
(16)

转子磁场定向时转差率：

(17)

(18)

则由式(18)可得无源控制率：

(19)

在式(19)中加入一项阻尼值，能够确保控制系统是严格无源的，减小所设计系统对不确定参数的敏感性，同时提高动态的响应能力，得到:

该过程即阻尼注入阶段，K表示阻尼系数。据学者Ortega的研究推得，阻尼系数的选取可参考[3]：

式中：0<ε

3.2 转速控制器

无源控制的交流异步电动机系统能逐渐趋于期望转矩，设立转速误差的反馈环，即能得到期望的转矩值：

式中:kp,ki的取值关系到所设计系统的稳定。

4 仿真结果及对比分析

实验过程：在MATLAB的仿真模块Simulink里分别搭建有速度传感器和无速度传感器系统模型，在给定转速下空载起动，0.5 s时加负载，得到如图5、图6、图7所示的仿真结果。

观察图5可知，无源异步电动机调速系统在有速度传感器时，起动阶段转速上升平稳，0.32 s达到额定转速；在0.5 s加负载时转速略有降低但迅速恢复，转矩随着上升至负载值时稳定。验证了无源异步电动机调速系统仿真模型是正确的，为后续进行无传感器的研究奠定了基础。

从图6中可以看出，无源异步电动机调速系统在基于磁链的MRAC情况下得到的系统响应逼近有速度传感器情况，但存在小幅波动，没有有速度传感器情况轨迹平滑，说明基于磁链MRAC无速度传感器的无源异步电动机调速系统基本可达到有传感器系统的调速控制效果，但控制精度略差，控制性能较低。

(a) 转矩响应

(b) 转速响应

(a) 转矩响应

(b) 转速响应

(a) 转矩响应

(b) 转速响应

图7为基于无功功率的MRAC无源异步电动机调速系统仿真图。由图7可知，电机转速响应快速且平稳，加负载后略有降低但随即恢复。起动转矩较大，加负载后转矩亦随着相应变化。与图6相比，基于无功功率MRAC的速度估算消除了磁链MRAC速度估算存在的低速段转速抖动问题，实现估算转速平滑地跟踪电动机实际转速，其控制性能要优于基于磁链MRAC情况。

5 结 语

本文从电机d，q坐标系的模型考虑，结合无速度传感器控制技术，由电气子系统的无源性设计异步电动机调速系统控制方案，由于不需要反馈观测器，故比较容易实现，具有无奇异点、全局较稳定、鲁棒性能高等特点。通过有速度传感器和无速度传感器的仿真对比，表明了无源性异步电动机调速系统在无速度传感器下也能实现很好的调速性能，并且体积小，重量轻，节约了成本。

[1] 程启明,程尹曼,王映斐,等.交流电机控制策略的发展综述.[J].电力系统保护与控制,2001,(9):145-154.

[2] 王涛,肖建,李冀昆.感应电机无源性分析及自适应控制[J]. 中国电机工程学报，2007，27(6)：31-34.

[3] ORTEGA R ,LORIA A，NICKLESSON P，et al. Passivity-based control of Eular-Lagrange system[M].New York：Springer，1998.

[4] CECATI C,ROTONDALE N.Torque and speed regulation of induction motors using thepassivity theory approach[J].Industrial Electronics,1999,46(2):119-127.

[5] 纪志成,薛华.感应电机自适应无源性控制方法及dSPACE实时仿真研究[J].西安交通大学学报，2004，38(12)：1220-1223.

[6] 侯祖峰,杨俊华,杨梦丽,等.感应电动机双闭环无源性跟踪控制[J]. 微特电机，2011,39(4):62-69.

[7] 顾亮，沈传文，季筱隆. 基于无源性的感应电机控制系统设计[J].电工电能新技术，2006，25(3)：42-45.

[8] 冯垛生,曾岳南.无速度传感器矢量控制原理与实践[M].北京：机械工业出版社,2006.

[9] 韩正之，陈彭年，陈树中.自适应控制[M].北京：清华大学出版社,2011.

[10] 廖东初，陈力，秦庆江,等.鼠笼式感应电动机无源性转速控制系统[J].微特电机，2013,47(5):1-3.

[11] 杨苹，陈武，刘穗生. 基于无源性理论的异步电动机转速控制[J]. 电力系统及其自动化学报，2007，19(2)：73-77.

Speed Regulation of Asynchronous Sensorless Motor Based on Passivity Theory

WANG Teng-fei，ZHANG Bin

(Lanzhou Jiaotong University,Lanzhou 730070,China)

Aiming at the problems like nonlinear, strong coupling, large disturbance of AC asynchronous motor, motor control systems were analyzed using the passivity theory from the point of energy exchange. The workless force was abstracted to simplify the controllers, and then a nonlinear dynamic control law which has global stability was obtained through the methods of energy-shaping and damping-injection. Simultaneously in order to avoid all kinds of trouble caused by traditional mechanical speed sensor, combined with the speed sensorless method of model reference adaptive control, the system was simulated in MATLAB, and compared with the case of speed sensor. The analysis shows the feasibility and validity of passive asynchronous motor speed regulation under the condition of sensorless.

asynchronous motor; speed sensorless; model reference adaptive control; passivity

2015-06-11

TM343

A

1004-7018(2016)03-0054-04