非对称双芯光子晶体光纤特性分析*

全新萍，励强华,辛成宇

(哈尔滨师范大学)



非对称双芯光子晶体光纤特性分析*

全新萍，励强华**,辛成宇

(哈尔滨师范大学)

设计一种新型非对称双芯光子晶体光纤模型，利用有限元法及其双芯光纤的耦合特性分析其光子晶体光纤的光学特性，数值模拟了非对称双芯光子晶体光纤的有效折射率、双折射、耦合系数在一定结构参数下随波长的变化特性.数值模拟结果表明，选择合适的结构参数可以得到较高的双折射特性以及耦合特性，因此光子晶体光纤的非对称结构的特性分析对于光学器件的研制有重要意义.

有限元法；耦合特性；非对称双芯光子晶体光纤；有效折射率；双折射；耦合系数

0 引言

近年来，随着光纤技术的发展，光子晶体光纤(photonic crystal fiber，PCF)受到越来越广泛地关注，由于其PCF的灵活结构特性使其具有普通光纤不具备的光学特点，如提出的新型高非线性色散平坦光子晶体光纤、双零色散光子晶体光纤等[1-3].通过改变其纤芯位置及包层的结构的不同设计可以得到所需要的光学特性，如灵活的非线性特性、高双折射特性、可控的色散特性、偏振保持特性等[4-6].

双芯光纤的特性近些年也比较热门，可变衰减器、光纤激光稳定性的窄带滤波器、双芯光纤的耦合特性等多被光学元件、光学传感器等领域利用[7-9].但由于双芯光纤的制作及其对于普通单芯光纤的耦合相对复杂及不可控，因此近些年利用光子晶体光纤的结构灵活性以及拉制方面的成熟技术，越来越多的人在PCF的基础上结合双芯光纤的结构来分析其光学特性，因此可以通过设计光纤的纤芯位置及包层的结构特性进一步研究所需要光学特性，使其达到PCF与双芯光纤的完美结合，即双芯光子晶体光纤(dual-core photonic crystal fiber，DC-PCF).付博等人在研究光子晶体光纤的特性方面已经通过理论模拟设计出了双芯高双折射光子晶体光纤[10].

该文设计了一种结构简单，易于制作的非对称双芯光子晶体光纤(如图1所示)，中心光纤易于与普通光纤耦合，设计的另一个纤芯可以调节偏振和耦合特性.利用有限元法对其非对称双芯PCF进行特性分析，通过调节其包层及纤芯的结构参量对有效折射率、双折射、进行分析并结合双芯光纤的耦合特性分析其耦合系数对其结构参数之间的变化.这种设计及分析对于光学器件的利用及特性分析有重要意义.

1 理论方法

关于双芯光子晶体光纤，目前还没有系统的分析方法,常见对于光子晶体光纤的数值分析方法有等效折射率模型、平面波展开法、超格子法、正交函数方法、有限差分法、有限元法等[11-14].该文认为利用有限元法对模型进行分析更反映双芯光子晶体光纤的光学特性有利于非对称结构PCF的分析，通过不同结构PCF的横向分布原理结合麦克斯韦理论进行分析，利用麦克斯韦方程组及边界条件

进一步控制变量来得出有效折射率neff及传播常数β，并对其光学性质进行分析.

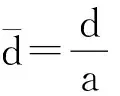
(1)

光纤的归一化频率V的表达式[15]为

(2)

2 理论模型与数值分析

图1为非对称双芯PCF截面的基模，两纤芯完全相同为分别去掉一个空气孔组成，一个纤芯在中心，另一个在侧面，包层是空气孔六边形结构，b=1.0 μm，Λ=2.0 μm，b为包层空气孔直径，Λ为孔间距，两纤芯距离为d，d=2Λ.

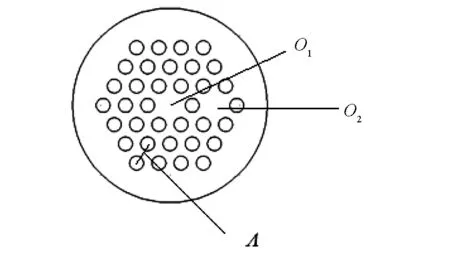
图1 双芯光子晶体光纤(O1、O2为纤芯，Λ为包层孔间距)

2.1 纤芯的有效折射率

利用有效原法通过对纤芯TE模、TM模的分析来进一步分析纤芯有效折射率随结构参数的变化，当b=1.0μm，Λ=2.0μm等结构参数不变，只改变波长λ从1.50 ～1.60μm范围内的有效折射率变化；让参数Λ=2.0μm，λ=1.55μm等参数确定只改变包层空气孔的半径b取0.9～1.1μm范围内的有效折射率的变化；当b=1.0μm，λ=1.55μm等结构参数不变时，只改变Λ从1.2～2.8μm，用有限元法分析有效折射率随Λ变化的规律.经过数值模拟，得出在双芯PCF两纤芯距离一定的前提下，得出有效折射率随着波长的增大是减小的，如图2、图3所示，当波长一定时，有效折射率随着包层空气孔半径b的减小而增大，有效光的模场多半被束缚在纤芯里；波长一定时有效折射率随着包层空气孔间距Λ的减小而减小，有效折射率和Λ成正比.从图中可知，当Λ=1.2μm时有效折射率随波长变化最明显，由此可知当其他结构参数不变时Λ越小，纤芯的光传播模式不只是束缚在纤芯里，而使纤芯有效折射率越来越接近于包层的有效折射率，部分光传播被分散到包层，导致两纤芯的束缚光强减弱 ,从而对双芯光子晶体光纤利用有一定的影响.

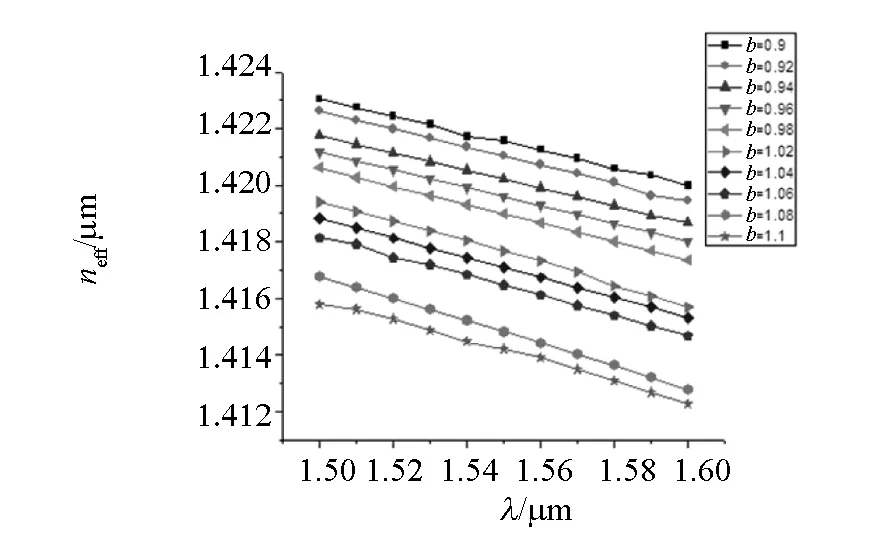
图2 改变b值的有效折射率随波长的变化

图3 改变Λ值的有效折射率随波长的变化

2．2 纤芯双折射

模式的双折射B是衡量PCF偏振性能的重要参数，因此对通讯信息方面有重要影响.由于双芯光子晶体光纤非对称的结构，影响双芯中光场的传播特性，与保偏光纤类似使其在正交模式下的x、y偏振方向上的不对称从而引起了双折射，基模的模式双折射表示为[16]，

(3)

由图4模拟分析了双芯光子晶体光纤的双折射度随光纤结构参数的变化，从图4可以看出，保持结构参数空气孔大小b=1.0μm，让空气孔节距Λ由1.2μm到2.8μm变化，当λ不变，光纤的双折射度随着Λ值的增大而减小，这是由于b不变时，随着Λ的增大光纤的纤芯面积增大，x、y方向纤芯不对性引起纤芯最内层空气孔的不对称性增强，因此双折射度随着空气孔节距的Λ的增大而减小.由图5可见，当结构参数Λ=2.0μm，改变空气孔直径由b=0.92μm到b=1.1μm变化.当λ不变时，光纤的双折射度随着b的增大而增大，由于包层空气孔的增大而让内层空气孔的不对称影响增大，使纤芯对光场的束缚增强.

从图4、图5可以看到当光纤的其他结构参数不变时，只改变波长，能看出光纤的双折射度随着波长的增大而增大，因为随着波长的增加，模场与外层空气孔作用增强，纤芯的不对称性增加，从而双折射度增大.当给定结构参数b=1.0μm，λ=1.55μm，Λ取值由1.2～1.6μm，双折射度由1.4×10-2～4.3×10-2，比文献报道的高一个数量级[17-18].

图4 改变Λ值双折射随波长的变化

图5 改变b值双折射随波长的变化

2.3 耦合系数

双芯光子晶体光纤适用于光学传感器[20]，其应用原理是利用双芯光纤的耦合特性，由该文模型通过理论分析方法可以得到耦合系数k，耦合系数是得到耦合长度的直接系数，直接反应了双芯光纤的耦合长度.图6的结构参数让d=2Λ，λ=1.55μm，两纤芯距离d=2.0μm等结构参数确定，只改变a=0.45μm到1.55μm，由图示可知纤芯半径与偶尔系数k的关系.由图可得到结构参数不变时，耦合系数是先减小后又逐渐的增大.由于是在纤芯半径逐渐变大过程中,光的有效模场被束缚在纤芯内,使模间的渗透变得困难;但是随着纤芯继续增大,两纤芯间距离变小,导模间渗透变得明显,反而使得耦合变得更加容易.由图7也可得双芯光子晶体光纤的耦合系数与两纤芯距离的关系特性，不难得到耦合系数随着纤芯距离的增大而减小.

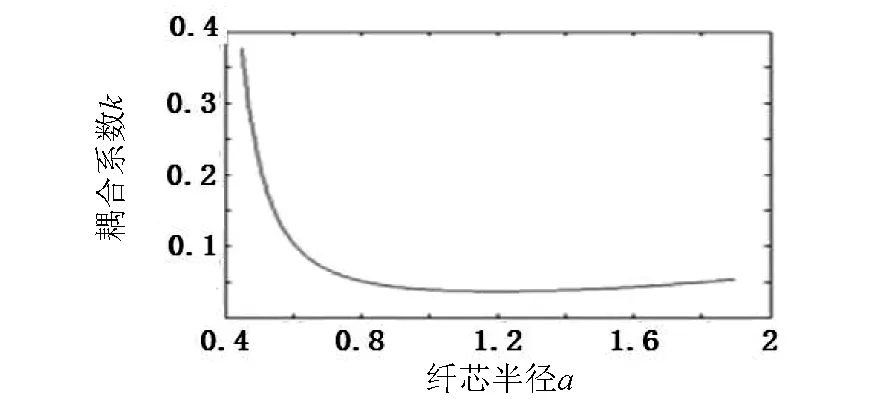
图6 纤芯半径随耦合系数的变化

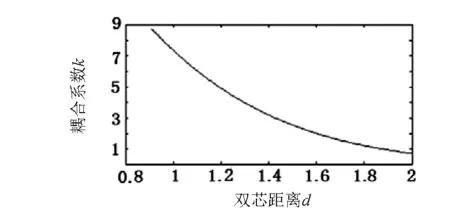
图7 两纤芯距离随耦合系数的变化

3 结束语

该文设计了一种非对称双芯光子晶体光纤理想模型并对其光学特性进行了理论分析.通过的光纤耦合性的分析得到双芯光纤的耦合系数随着两纤芯距离逐渐减小，随着纤芯半径先减小后增大；光纤的有效折射率随包层结构参数的变化来判断双芯光纤纤芯的通光性质；双折射B随着波长的增大而增大，当波长不变时B随着包层孔间距Λ的减小而增大，随着孔半径的增大而增大.通过数值模拟在结构参数一定时可以得到较好的耦合特性与保偏特性，与普通双芯光纤相比有较高的双折射度，与普通光子晶体光纤比具有较好的耦合性，结合了光子晶体光纤与双芯光纤的优点，有利于光学器件的研制，另也在为非对称双芯光纤的理论分析方面提供有一定的基础，这在以后双芯光子晶体光纤的应用方面起到更加完善的作用.

[1] Knight J C，Awiaga J, Briks T A, et al. Recent Progress in Photonic crystalfiber[J]. IEEE Photon Technol Lett, 2000, 12807.

[2] 姜凌红，侯蓝田.双零色散光子晶体光纤结构参数的变化对其性能的影响[J].Acta Physica Sinica，2010,59(2):1095-06.

[3] 杨昌喜，Claire Gu，金国潘.一种新型高非线性色散平坦光子晶体光纤结构[J].Acta Optica Sinica,2006,10：1569.

[4] Briks T A，Knight J C，Russell P S J，et al. All-scillca single mode Optic fiber with Photonic crystal cladding[J]. Opt Lett,1996,21,1547.

[5] Knight JC，Briks T A，Russell P S. Large mode area Photonic crystal fiber[J]. Opt Lett,1997,22 961.

[6] Tian H D,Yu Z Y,Han L， et al. Lateral Strecs-induced Proagtion characteristics in Photonic crystalfibers[J]. Chin Phys B,2009:18-1109.

[7] 吴万青，徐峰，陈博，等.一种非对称双芯光子晶体光纤耦合器[J].Acta Optica Sinica，2009(12)：3527 04.

[8] Libo Yuan，Xue Wang. Four beam single fiber optic interferometer and its sensing characteristics[J].Sensors and Actuator,2007,138(A):09-15.

[9] Pavel P, Kanka J.Erbium-doped twin core fiber narrow band filter for fiber lasers[J].Opt Quant Electron, 2001,33:571-581.

[10] 付博，李曙光，姚艳艳，等.双芯高双折射光子晶体光纤耦合特性研究[J].物理学报，2009，58(11)：7708.

[11] 张晓娟，赵建林，崔莉.一种高双折射光子晶体光纤的模式特性分析[J].Acta Optica Sinica,2008(7):1379.

[12] 佘守宪.导波光学物理基础,2002.

[13] Wang Zhi，Ren Guobin，Lou Shuqi et al．The mode characteristics of the photonic crystal fibers[J]．Acta Optica Sinica，2004(24):324-328.

[14] Brechet F，Marcou J，Pagnoux D, et al.Complete analysis of the characteristics of propagation into photonic crystal fiber by the finite element method[J]．Optical Fiber Technol,1999,6(2):181-191.

[15] 阿戈沃.非线性光纤光学原理及应用[M].贾东方译.北京：电子工业出版社,2002.318-322.

[16] 龚桃荣，严凤平，王琳，等.高双折射光子晶体光纤特性分析[J].中国激光,2008,35:559.

[17] 李曙光，邢光龙，周桂耀，等.空气孔正方排列的低损耗高双折射光子晶体光纤的数值模拟.物理学报，2006,55:238.

[18] 张明明，马秀荣，曹晔，等.高双折射光子晶体光纤研究[J].光子学报,2008,37:1126.

(责任编辑：李家云)

Research on the Characteristic of Unsymmetrical Dual-Core Photonic Crystal Fibers

Quan Xinping, Li Qianghua,Xin Chengyu

(Harbin Normal University)

In this paper, a new unsymmetrical dual-core photonic crystal fiber model is designed, by using finite element method and its twin-core fiber coupling characteristics of the optical properties of the photonic crystal fiber. The variation of the wavelength of effective index of refraction, birefringence, coupling coefficient that unsymmetrical dual-core photonic crystal fiber with certain structural parameters are numarically simulated. The results show that the choice of appropriate structure parameters can obtain high birefringence characteristics and coupling characteristics. Therefore, the analysis of the characteristics of photonic crystal fiber with asymmetric structure has important implications for the development of optical devices.

Finite element method；Coupling characteristic；Unsymmetrical dual-core photonic crystal fiber；Effective index of refraction；Birefringence；Coupling coefficient

2016-01-03

*黑龙江省自然科学基金(ZD201401)

**通讯作者：lqh0118@126.com

O436

A

1000-5617(2016)02-0088-04