三维可视化在经典优化算法中的应用

李辉辉,刘延龙

(东北林业大学)



三维可视化在经典优化算法中的应用

李辉辉*,刘延龙

(东北林业大学)

三维可视化(科学可视化)已经成为现代科学研究的重要课题之一，多维函数问题在现实生活中层出不穷，将多维函数问题进行降维从而应用在三维可视化中就成为解决多维问题重要的一步.这个过程最主要的就是要求通过适当的降维方法将大量的多维数据降到人们能够利用或者方便处理的程度.根据规划中目标函数的线性性，线性降维算法和非线性降维算法已经成为解决多维函数问题的主要方法，将通过经典优化算法将非线性无约束规划问题进行降维，从而使该类多维问题在三维图像中实现可视化.

三维可视化;降维;非线性无约束规划

0 引言

计算科学与信息技术[1]已经历经了几十年的发展，给人类社会的发展带来了极大的影响.随着现代的数据采集、数据储存以及数据管理等技术的日趋成熟，人们获取和收集数据的能力得到了巨大的提升，获取的数据数量正以指数级的形式增加.无论是科学研究领域还是社会生活等方面都积累了大量复杂的数据.在科学研究和实际工程中，很多数据集具有多维的特点.如：图像分析、计算机视觉、地震属性、三维模型的分类与检索.这些多维特征能够提供更为丰富和详细的信息，理论上会给提高算法的准确性带来很大帮助.这些丰富的数据资料给人们带来便利但同时也带来了一大堆的难题，比如信息过量、数据难以处理、有价值的信息淹没在海量的数据中、数据难以取舍等.面对“过多”的数据信息，如果缺乏合理的分析和处理手段，就无法发掘出数据中隐含的潜在系和规则，也无法据此对未来的发展趋势做出预测.这就直接导致所谓的“数据富但知识匮乏”的现象.因此，如何对这些丰富的数据资源进行合理的分析，挖掘出数据中蕴含的有效信息已经成为研究者和技术专家所面临的挑战.为了解决这一问题，可以首先将数据降到低维空间，然后得到低维特征进行既定的学习或者挖掘任务.有效的数据降维技术能够探索出原始数据的内在结构和联系，不仅可以消除数据间的冗余，以简化数据，提高计算效率，还能够大大改善数据的可理解性，提高学习算法的精度.

降维算法间接地将多维问题进行了转化，使得多维问题更加容易被研究，而将多维问题进行降维在三维图形中可视化[2]使得研究结果更加清晰，从而让人们更直接的解决多维问题.根据多维问题的线性性，将降维算法分为线性降维算法和非线性算法.线性降维算法包括：PCA主成分分析[3]和LDA线性判别分析[4]等，非线性降维算法包括：SOFM自组织特征映射、主曲线以及LLE局部线性嵌入ISOMAP等距映射和LE拉普拉斯特征值映射等.该文将从非线性无约束问题规划入手，研究降维算法，改进并进行应用.

1 降维算法

1.1 n维欧氏空间定义

设V是实数域R上的线性空间(或称为向量空间)，如果对V中的任意两个元素α,β确定的实数(α,β)与它们对应，且满足如下关系：

(1)(α,β)=(β,α);

(2)(kα,β)=k(α,β),k∈R;

(3)(α+β,τ)=(α,τ)+(β,τ),τ∈V.

(4)(α,α)≥0,当且仅当α=0时,(α,α)=0.

则称(α,β)为α与β的内积，定义了内积的线性空间V称为欧几里得空间，简称为欧氏空间.所以说空间可以被扩展来应用于任何有限维度，而这种空间就叫做n维欧几里得空间(简称n维空间)或有限维实内积空间.

1.2 超平面[5]的定义

超平面是指n维欧氏空间中余维度等于1的线性子空间，它是由平面中的直线、空间中的平面在n维欧氏空间中的推广得来的，在形如{x/aTx=b}的一个集合中，其中a是欧氏空间Rn中的一个非零向量，b是一个标量，这个集合就叫作n维欧氏空间中的超平面.超平面是从n维空间到n-1维空间的一个映射子空间，它有一个n维向量和一个实数定义.

1.3 n维欧氏空间向量的二范数

范数是表示具有“长度”概念的函数.在泛函分析、线性代数及相关的数学领域中它指的是一个函数，它表示为矢量空间内的所有矢量赋予非零的正长度或大小.

若X是数域K上的线性空间，泛函‖·‖： X→R满足：

(2)正齐次性：‖cx‖=|c|·‖x‖,c∈R.

(3)次可加性(三角不等式)：‖x+y‖≤‖x‖+‖y‖.

那么‖·‖称为X上的一个范数.范数与内积、度量、拓扑是相互联系的.

n维欧氏空间向量的2-范数：

设x=(x1,x2,…,xn)， ‖x‖2=(|x1|^2+

|x2|^2+…+|xn|^2)^1/2

1.4 克莱姆法则

1.5 基本思路

已知X(0)和L，其中 X(0)是欧式空间中超平面上的一点，L是这个超平面的一个法线方向，求过X(0)点的某单位向量 α和β，使得α⊥L、 和β⊥L.由此可知，超平面上的任意一点都可由α和β这两个向量和定点X(0)来确定，利用α和β则可构建三维图像，从而使多维函数实现可视化.

具体策略如下[6]：

由超平面定义 ，有

(X-X(0))TL=0

(1)

由于L≠0∈Rn,设lj=max(|l1|,|l2|,|l3|，…,|ln|),必有lj>0,

又令

(2)

将(2)式带入(1)式有

(3)

(4)

设lk=max(|l1|,…,|lj-1|,|lj+1|,…|ln|)

(5)

将(5)式代入(1)式可得

(6)

由α⊥β以及(2)式和(5)式，可得

(X(1)-X(0))T(X(2)-X(0))=0

(2-n)·lj

(7)

根据克莱姆法则：

(10)

此时，n维函数F(X)的自变量取值范围：

X=Cα·α+Cβ·β+X(0)

(11)

式中Cα、Cβ均为某一取值范围，例如：(-0.5,0.5)等.

综上可知：根据1可以计算出α、β两个向量，以Cα、Cβ两个变量得出X，从而知道f (X)，运用matlab程序[7]绘制以Cα、Cβ和f(X)为坐标的三维图形，从而使非线性无约束规划在三维空间实现可视化.

2 算法仿真实验

式中X(0)=[1.0,1.0,1.0,1.0]T

L(1)=[0.5,0.8,0.1,0.3]T

L(2)=[0.5,-0.8,0.1,-0.3]T

Cα和Cβ均属于(-0.7，0.7).

当L(1)=[0.5,0.8,0.1,0.3]T时， 得图1所示图像.

图1 垂直于L(1)方向的f1(X)的三维图像

当L(2)=[0.5,-0.8,0.1,-0.3]T时，得图2所示图像

图2 垂直于L(2)方向的f1(X)的三维图像

式中X(0)=[1.2,1.2,1.2,1.2]T,

L(1)=[0.9,0.2,0.5,0.7]T,

L(2)=[-0.9,0.2,-0.5,0.7]T.

Cα和Cβ均属于(-0.9,0.9).

当L(1)=[0.9,0.2,0.5,0.7]T时， 得图3所示图像.

图3 垂直于L(1)方向的f 2(X)的三维图像

当L(2)=[-0.9,0.2,-0.5,0.7]T时， 得图4所示图像.

图4 垂直于L(2)方向的f 2(X)的三维图像

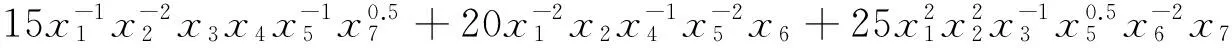
式中X(0)=[0.8,0.8,0.8,0.8,0.8,0.8,0.8]T;

L(1)=[0.1,0.3,0.5,0.7,0.9,0.6,0.4]T;

L(2)=[-0.1,0.3,-0.5,0.7,-0.9,0.6,-0.4]T,

Cα和Cβ均属于(-0.6，0.6).

当L(1)=[0.1,0.3,0.5,0.7,0.9,0.6,

0.4]T时，得图5所示图像.

图5 垂直于L(1)方向的f 3(x)的三维图像

当L(2)=[-0.1,0.3,-0.5,0.7,-0.9,0.6,-0.4]T时， 得图6所示图像.

图6 垂直于L(2)方向的f3(X)的三维图像

3 降维算法的改进

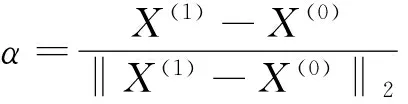
从而可知在上述算法中α、β是由L确定的，如果将(2)和(5)式中的1变为属于(0，1)的任意数r，则对该种降维算法进行了改进.具体策略如下：

设r∈(0,1)，有

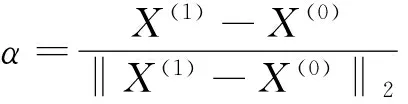
就例1L(1)=[0.5,0.8,0.1,0.3]T方向来研究：

当r不同时的四种三维图形(如图7-10所示)的比较：

图7 当r=1时f 1(X)的三维图像

图8 当r=0.1时f1(X)的三维图像

图9 当r=0.5时f1(X)的三维图像

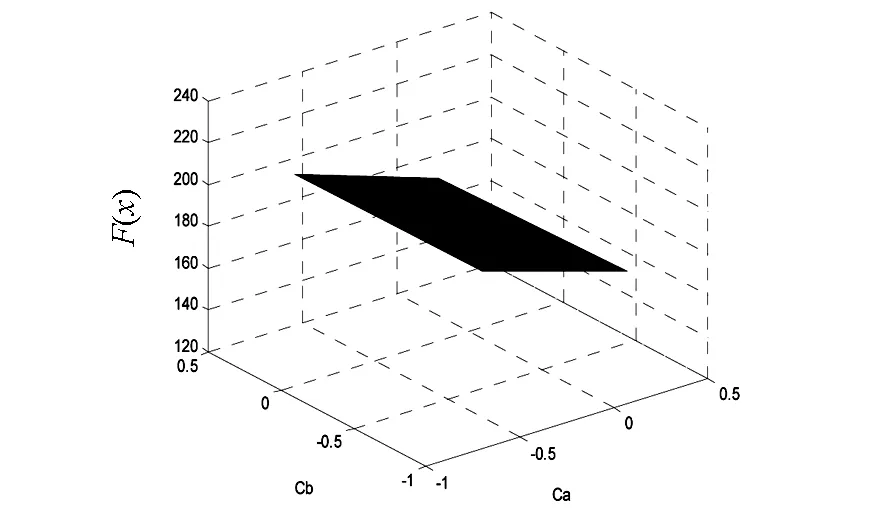
图10 当r=0.9时f1(x)的三维图像

由此可知，r的取值直接影响到了绘制出的图形.随着r的变化，按照matlab程序所绘制出来的图形是不一样的，从而也说明了该非线性无约束规划的解也受到了影响.从图形的比较中可以看出在解的影响上该文所描述的降维算法中设定条件占了很大一部分原因.

4 结束语

随着计算机技术的发展，多维数据问题在现实应用中层出不穷，三维数据可以在人脑中产生图像便于分析，而多维的数据很难让人们直接理解，所以在医学、科学研究、建筑学、气象学、生物学等方面的各种应用中出现的多维数据能够通过降维算法进行降维，用三维图像的形式展示出来则可以给实验研究带来很大的方便[8].该文在基于使多维函数实现三维可视化的基础上，分析了一种降维算法的具体方案.论文的研究方法通用性极高，但根据论文中降维算法的研究也发现此降维算法对规划问题中解的可行性对已知条件有很强的依赖性.

[1] 乔立山. 基于图的降维技术研究及应用[D]. 南京：南京航空航天大学, 2009.

[2] 石教英. 科学计算可视化算法与系统[M].北京：科学出版社, 1996.

[3] Timmerman M E. Bookreview. Principal Component Analysis (2nd ed.). I.T. Jolliffe. New York: Springer-Verlag, 2002. ISBN 0-387-95442-2. XXIX + 486 pp.[J]. Journal of the American Statistical Association, 2003, 464,vol.98.

[4] Belhumeur P N, Hespanha J P, Kriegman D J. Eigenfaces vs. Fisherfaces: Recognition using class specific linear projection[J]. IEEE Transactions on Pattern Analysis & Machine Intelligence, 1997, 19(7):711-720.

[5] 余建明, 姜广峰. 超平面构形的可约性[J]. 中国科学,2006(12):1422-1430.

[6] 邓扬晨, 张卫红, 钱卫,等. 多维函数图形的一种三维可视化方法[J]. 西北工业大学学报, 2003, 21(3):368-371.

[7] 赵海滨. MATLAB应用大全[M]. 北京：清华大学出版社, 2012.

[8] 宋靓. 降维方法及非线性降维方法举例[J].中国高新技术企业, 2011(10):46-47.

(责任编辑：于达)

The Application of 3D Visualization in Classical Optimization Algorithm

Li Huihui， Liu Yanlong

(Northeast Forestry University)

Three-dimensional visualization has become one of the important subjects of modern scientific research. Multidimensional function has become an endless problem in real life. It is an important step for the dimensionality reduction of the multi-dimensional function applying into the 3D visualization, and the main requirement of this process is through the proper method of dimensionality reduction to make a lot of multidimensional data more convenient for people to use or much easy to deal with. According to the linear programming in objective function, linear dimensional reduction algorithm and nonlinear dimensional reduction algorithm have become the main method to solve the problem of multi-dimensional function. In this article, dimensionality reduction of unconstrained nonlinear programming through classical optimization algorithm is realized, which makes this kind of multidimensional problems visualized in the 3D image.

Three-dimensional visualization; Dimensionality reduction; Nonlinear unconstrained programming

2016-01-09

*通讯作者：1163727319@qq.com

O18

A

1000-5617(2016)02-0023-06