一种非线性可燃物含水率模型的线性化方法*

季俊超,宫智耀,庞靓璠,张 燕,曲智林

(东北林业大学)



一种非线性可燃物含水率模型的线性化方法*

季俊超,宫智耀,庞靓璠,张 燕,曲智林

(东北林业大学)

利用泰勒展开的的方法给出一种将非线性可燃物含水率模型线性化的方法，进而给出了基于logistic函数可燃物含水率模型参数的估计方法，由此得到一种线性化的可燃物含水率预测模型.通过实验数据检验，给出的线性化可燃物含水率模型的准确率达到97%(相对误差不超过5%)，说明该非线性可燃物含水率模型的线性化方法是可行的，由此得到的线性化可燃物含水率预测模型可以用于预测可燃物含水率变化规律.

可燃物;含水率;预测模型

0 引言

可燃物含水率的大小可以用来判断林火发生的难易程度，因此研究森林可燃物含水率变化规律对于控制林火蔓延速度和预报森林火险都有非常重要的作用.通过建立数学模型来研究可燃物含水率变化规律是一种有效的方法，而以平衡含水率为基础建立的可燃物含水率模型一般都是微分方程，模型中的平衡含水率有的是用线性函数描述的，如曲智林[1]等，有的是用非线性函数描述的，如Byram(1963)[2]，Viney(1991)[3-4]，Simard[5]，Van Wagner[5]，Nelson[6]，Anderson[7]，金森(1999)[8-9],曲智林[10]等，而用非线性函数描述的可燃物函数率更加真实可靠，但在实际应用中模型的参数是很难估计的，这对于预测可燃物含水率变化带来了困难.该文将针对基于logistic 函数的这种非线性可燃物含水率模型给出其线性化的方法，进而给出估算模型参数的方法.这些研究对于非线性可燃物含水率模型的应用是非常有意义的.

1 理论推导

1.1 线性化推导

根据文献[5]的研究表明，森林可燃物含水率的变化模型为:

(1)

其中: Mt为t时刻的可燃物含水率(%)；E0为t时刻的可燃物平衡含水率(%)；k为模型参数.

根据以往研究：可燃物的平衡含水率主要与大气中的相对湿度、风速和温度有关[11],即

Et=f (Tm,Hn,Wl)

(2)

其中:T为温度(℃)；H为大气中的相对湿度(%)；W为风速(级).将连续模型(1)式进行离散化变形，得

(3)

令Δt =1，则可以得到可燃物含水率的预测模型

Mt+1=(1-k)Mt+kEt

(4)

不难发现，想要将非线性可燃物含水率模型(4)线性化只需将Et展为线性形式，于是，将(2)式在点(0,0,0)处展开，有：

(5)

再代回到模型(4)中得到

(6)

至此，将非线性化模型化为线性模型.

1.2 参数估计

若己知可燃物含水率和气象因子的实时观测数据(Mt+1,i，Mt,i，Tm,j,Hn,j,W1,j),(i=1,2,…,n),m时刻气温，n时刻的相对湿度和l时刻的风速来预测t+1时刻的可燃物含水率.令

(7)

根据线性最小二乘原理，由正规方程组的解就可作为模型(6)中参数的估计值.

2 模型的验证

2.1 数据的选取

该文进行研究所利用的观察数据的来源为2009年3月20日至2009年4月20日黑龙江海林市石河子林场试验地(北纬43°28＇～45°69＇,东经128°3＇～130°47＇ ).采集的数据包括时间、温度、风速、相对湿度、可燃物含水率、风向以及降水量等数据.

通过统计林场试验地的观测数据，得到了各影响因子的取值范围，见表 1.

处理数据均使用STATISTICA6．0软件完成.

表1各影响因子取值范围

2.2 基于logistic曲线的可燃物含水率线性化模型

根据文献[12]的研究表明：平衡含水率的变化规律遵循logistic曲线，即温度、相对湿度等气象条件决定可燃物平衡含水率最高接近极限值Emax,最小接近或者可以达到0.因此选择的平衡含水率为

(8)

其中：Mt为t时刻的可燃物含水率(%)；Et为t时刻的可燃物平衡含水率(%)；k为模型参数；Emax为平衡含水率的最大值，该文Emax=100,A,a,b,c为待定参数.将上式代入到公式(4)中，即可以得到可燃物含水率预测模型

(9)

由1.1中线性化推导过程可知，为了将上述方程(2)展开成线性关系,只需对Et进行泰勒展开为线性形式，

≈(A-2A2)(aTt-k1+bHt-k2+cWt-k3)+A2-A+1.

(10)

将该结果代入(9)，则得到非线性可燃物含水率模型线性化后的含水率模型为：

Mt+1≈(1-k)Mt+kEmax[(A-2A2)(aTt-k1+bHt-k2+cWt-k3)+A2-A+1]

(11)

利用此模型，t+1时刻的可燃物含水率可由t时刻的可燃物含水率、t-k1时刻的气温、t-k2时刻的相对湿度和t-k3时刻的风速算得.

2.3 模型中参数的估算方法

若己知可燃物含水率和气象因子的实时观测数据(Mt+1,i，Mt,i，Tt-k1,i,Ht-k2,i,Wt-k3,i),(i=1,2,…,n),t-k1时刻气温，t-k2时刻的相对湿度和t-k3时刻的风速来预测t+1时刻的可燃物含水率.根据非线性最小二乘原理，令

得到方程组

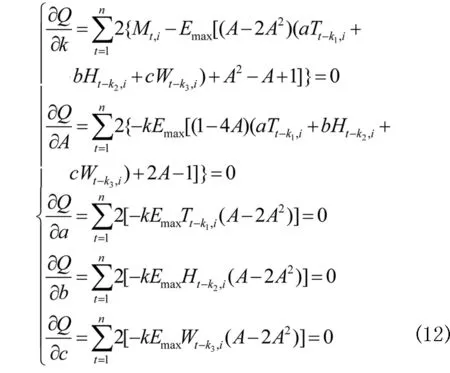
利用STATISTIC6.0软件解出此正规方程组的解就可作为模型(11)中的参数 的估计值.

2.4 模型的建立

2.4.1 可燃物单位时间内含水率改变量与各影响因子的相关性分析

为了确定模型中的反应时间k1、k2、k3，可以先对试验地各个观测变量进行相关性分析，该文利用试验地3月20日至3月28日的观测数据(共200个样本)并结合偏相关系数公式：

(13)

确定了单位时间内可燃物含水率变化量与之前各个时段内空气中温度、相对湿度和风速等影响因子的相关性关系.

由表2中可得：该可燃物1h内的含水率改变量与前2 h的气温值相关性较高，并呈负相关；与前1 h的相对湿度相关性较高,并呈正相关；与前3 h的风速值相关性最高，并呈负相关.由此可以说明，气象要素中的气温、相对湿度和风速对可燃物含水率变化的影响有一定的滞后性，因此，针对该文的研究所要选择的气象因子为前3 h的气温、前1 h的相对温度和前3 h的风速，即公式(11)中k1=2,k2=1,k3=3.

表2 单位时间內含水率改变量与不同时间段的温度、相对湿度和风速的相关性

2.4.2 模型参数估算与模型验证

该文依据林场试验地的200个观测数据建立了模型，并根据线性最小二乘原理，按照该文1.2中方法步骤，对模型(11)的参数进行估算(见表3).以上模型均通过t检验(α=0.05).

表3 模型中参数的估计值

即得到可燃物含水率预测模型：

Mt+1=0.926Mt+0.74×100×[0.044×

(-0.043Tt-2+0.023Ht-1-0.653Wt-3)+0.752]

(14)

模型(14)表示可以用t时刻的可燃物含水率、t-2时刻气温、t-1时刻的相对湿度和t-3时刻风速来预测t+1时刻的可燃物含水率.

为了说明模型的精度，对模型(14)进行了检验.检验发现，选取200个试验地的观测数据，其正确率达到97%(相对误差不超过5%).并给出了林场试验地2009年3月28日可燃物含水率的实测值、预测值和误差值(见表4)

由表4中的数据可见，该文建立的模型能够较准确地对试验地的可燃物含水率进行预测，说明该模型是可行的，能够在实际中进行应用.

3 结束语

在基于 logistic曲线建立可燃物含水率模型的基础上，利用泰勒展开实现非线性可燃物含水率模型的线性化，并利用最小二乘法对模型参数进行估计，经检验发现，模型的准确精度达97% (相对误差不超过5%)，说明在多时无雨条件下，利用该模型可以预测可燃物含水率的变化,并且一定程度上解决了平衡含水率的参数估算的困难，证明了所采用的方法是可行的.但对模型参数进行估计时，在求解正规方程组时可能会出现多个解，因此在利用STATISTICA6.0软件求解方程组时应给定好初始值.另外，应指出模型建立在多时无雨的情况下，具有一定的局限性；选用的影响因素只有温度、相对湿度和风速，对其他因素没有考虑；同时，该文是针对特定可燃物进行研究，对于不同类型可燃物的含水率模型是不同的，但方法是可以借鉴的.

表4 2009年3月28日试验地可燃物含水率的实测值、预测值和误差值

[1] 曲智林，吴娟，闵盈盈.具有时滞的可燃物含水率预测模型[J]．东北林业大学学报，2012，40(3):120-122．

[2] Byram G B.An analysis of the drying process in forest fuel material[J].Unpublished report,USDA Forest Service,Southern Forest Fire Laboratory,Macon,GA,USA,1963.

[3] Viney N R,Catchpole E A.Estimating fuel moisture response time from field observations [J].International of Wildland Fire,1991,1(4):211-214.

[4] Viney N R.A Review of Fine Fuel Moisture Modeling[J].International Journal of Wildland Fire,1991,1:215-234.

[5] 刘曦，金森.平衡含水率法预测可燃物含水率的研究进展[J]．林业科学,2007,43(12):126-133．

[6] Nelson R M，Jr． Prediction of diurnal change in 10 h fuel stick moisture content[J].Canadian Journal of Forest Research，2000，30(7):1071- 1087．

[7] Anderson H E． Moisture diffusivity and response time in fine forest fuels[J]． Canadian Journal of Forest Research，1990,20(3):315-325．

[8] 金森，姜文娟，孙玉英．用时滞和平衡含水率准确预测可燃物含水率的理论算法[J].森林防火,1999,4:12-14.

[9] 金森，李亮.时滞和平衡含水率直接估计法的有效性分析[J]．林业科学，2010,46(2):96 -102．

[10] 曲智林，李昱烨，闵盈盈.可燃物含水率实时变化的预测模型[J]．东北林业大学学报,2010,38(6):66-67.

[11] Nelson R M. Prediction of diurnal change in 102hour fuel moisture content[J]. Canadian Journal of Forest Research，2000，30:1071-1087.

[12] 尹坤.基于logistic曲线的森林可燃物含水率模型[D].东北林业大学，2015.

(责任编辑：季春阳)

A Linearization Method for Nonlinear Fuel Moisture Content Model

Ji Junchao,Gong Zhiyao,Pang Liangfan,Zhang Yan,Qu Zhilin

(Northeast Forestry University)

In this paper, a linearization method for nonlinear fuel moisture content model is presented by Taylor’s theory，and then the method of estimating parameters from the fuel moisture content model based on the logistic function is given, thus a linear model for predicting the fuel moisture content is obtained.Through experimental data testing,the established linear model had an average precision of 97%(the relative error is no more than 5%),which means that the linearization method of the nonlinear fuel moisture content model is feasible,and the resulting linear fuel moisture content prediction model can be used to predict the changing patterns of fuel moisture content.

Forest fuels; Moisture content; Prediction model

2016-01-21

*东北林业大学大学生创新创业训练计划项目(201510225159)

S762.1

A

1000-5617(2016)02-0065-04