隧道周边共线径向双裂纹的应力强度因子数值分析

付杨成, 朱哲明, 刘凯, 范勇

(四川大学建筑与环境学院, 成都610065)



隧道周边共线径向双裂纹的应力强度因子数值分析

付杨成, 朱哲明, 刘凯, 范勇

(四川大学建筑与环境学院, 成都610065)

隧道周边围岩结构复杂，如节理、地裂缝等，势必会对隧道的安全造成一定的负面影响。利用Abaqus软件，对双轴压缩情况下，隧道穿过不同位置的地裂缝的情况进行了数值模拟，分析研究了裂缝倾角α、裂缝长度l以及隧道侧压力系数λ对两个裂纹尖端应力强度因子及隧道稳定性的影响。结果表明：(1)裂纹倾角、裂缝长度、侧压力系数对裂尖应力强度因子的影响明显，隧道周边径向双裂纹大大削弱了隧道的强度及稳定性；(2)由于隧道构形的影响，上下两裂尖的应力强度因子分别在倾角为45°和52°达到最大值，需要特别注意在裂纹倾角45°～52°附近隧道的安全性；(3)侧压力系数在0.8～1.2范围内有削弱裂纹尖端应力集中的作用，有利于隧道的安全性；(4)当裂缝长度与隧道宽度比例超过5倍时，应主要考虑裂缝对隧道安全性的影响。

隧道；共线裂纹；应力强度因子；强度；稳定性

引言

由于地质状况的复杂性，隧道往往需要穿越各种构造地形，如节理、天然断层等。另外，在隧道以爆破的方式掘进过程中，也会在隧道周边产生大量的径向裂纹。在隧道建成使用后，由于自身重力场和构造应力场以及其他外来载荷的作用，会萌发新的裂纹，而先前产生的裂纹也可能会进一步扩展。显然，这些裂纹对隧道的强度和稳定性有一定的负面影响，并可能进一步引发事故与灾难。研究不同状态下的多条裂纹的相互作用，特别是多条裂纹对隧道的影响，对于工程实际具有重要的指导意义。

对于隧道周边围岩在特殊构造下的稳定性，国内外学者做了很多相关方面的研究。张志强等[1]结合细观层面的节理形态和变化，并通过数值模拟，指出节理面对岩体的力学性质有很大的削弱作用，并严重影响隧道的稳定性。认为剪切滑移区是导致岩石发生破坏的主要因素，提出将剪切滑移区作为节理岩体处隧道稳定性的可量化判定指标。Charpentier等[2]认为，地下工程的实施将导致应力在开放处进行重分布，这会导致裂纹的产生和破坏。他们通过进行隧道开挖对其周围页岩的微裂纹形成影响的试验，并将其与构造破裂进行对比，并指出，岩体的孔隙度、节理和各向异性，对岩体的破坏有很大的影响。贾蓬等[3]对在不同倾角层岩中的隧道的稳定性进行了数值研究，结果表明，层状结构的倾角对隧道围岩的稳定性有显著影响，随着倾角的增大，隧道周边围岩的应力分布的非对称性增强，也导致了破坏模式的非对称性。

晏启祥等[4]绘制了不同位置的裂纹下的盾构隧道应力强度因子的包络线，并与钢筋混凝土结构的断裂韧度进行对比，从而将断裂理论应用到含裂纹盾构隧道的安全性评价中。方秦等[5]认为混凝土损伤塑性模型能够较精确地模拟混凝土材料的双轴应力状态，对在双轴应力状态下的该材料破坏的应力包络图能较好地反映。王蒙等[6]采用光弹实验和数值方法，讨论了隧道围岩裂纹角度和荷载对裂纹尖端应力强度因子的影响，并得出在单轴压缩载荷作用下，裂尖应力强度因子随裂纹倾角的增大而增加，并在60°后开始减少；在围压作用下，45°倾角的裂纹为对隧道安全最不利的裂纹等的结论。彭建兵等[7]对马蹄形隧道在40°斜穿地裂缝的破坏机制进行了试验研究。试验结果表明，在该情况下隧道的破坏形式为扭转、弯曲和剪切变形的综合破坏，且破坏形式不对称；并指出马蹄形隧道40°斜穿地裂缝时，适宜采用分段方式来分别应对扭转、弯曲和剪切变形，需要注意加强结构的抗扭设计，通过扩大端面或者提高混凝土强度等级等措施来抵抗剪切变形。李占海等[8]通过数值模拟，分析了侧压力系数λ对马蹄形隧道的损伤破坏的影响。结果表明，隧道的损伤机制与侧压力系数密切相关，当λ值较小时，初始损伤主要分布于拱脚、拱肩和拱顶位置，且裂纹主要沿垂直方向开裂；当λ值较大时，初始损伤主要集中在拱顶部位，破裂模式也转变为水平开裂。范君黎等[9]结合模型试验与数值模拟，研究了高宽比K对马蹄形隧道围岩稳定性的影响。研究结果表明，隧道围岩稳定性受隧道高宽比的影响明显，对于无裂纹隧道模型，试件的抗压强度在K=1.5时达到最大，K=1.0时最小；而对于含与垂直方向成130°角的单裂纹的隧道，K值约在1.7时的抗压强度最大，约在0.7时最小。李元鑫等[10]研究了拱肩处裂纹方向对直墙拱形隧道的稳定性的影响。数值模拟和模型试验均表明，拱肩处裂纹会降低隧道的强度与整体稳定性，且影响程度与裂纹倾角有关，在裂纹方向与垂直面呈60°和130°时，裂纹对隧道稳定性的削弱程度最大，其裂纹尖端的应力集中现象也最为明显。朱哲明等[11-15]基于复变函数方法，推导含裂纹的材料的应力函数表达式，并进一步结合边界配位法，计算得出应力强度因子，其结果与数值模拟结果吻合良好，并与实验结果相印证；提出了含裂隙的脆性材料在双向压缩载荷作用下的破坏准则，且该准则可被简化后转化为最大剪应力准则。

国内外学者对隧道周边裂纹及其稳定性的研究已经很多，但对于多条裂纹的情况，由于相对于单一裂纹而言，更接近实际，且有裂纹间的相互影响，组成类型众多，情况复杂等多种条件限制，还可以进一步研究。本文选择了含多条周边裂纹的隧道中的一种较为简单的情况，即含共线径向裂纹的隧道进行了数值模拟与模型试验研究，研究在该情况下的隧道的强度及稳定性。

1模型的简化及参数的选取

考虑直墙拱形隧道穿过有一定倾角的地裂缝的情形，在这里简化为隧道两侧的径向共线双裂纹，且设定半圆圆心至两个裂尖的距离相等，如图1所示。

图1隧道及双裂纹模型

设定外边界分别受到法向均布压力的作用，尺寸为400 mm×400 mm的正方形。隧道宽度为4 mm，依据范君黎等[9]的实验与模拟结果，采用高宽比K=1.5的隧道，即半圆半径为2 mm，下方为正方形。

分别考察裂纹倾角α、圆心至裂尖的距离l、侧压力系数λ这三个因素对隧道的强度和稳定性的影响。基于控制变量法的思想，设计具体思路为：考察裂纹倾角的影响时，设定圆心至裂尖的距离为6 mm，竖直压力为10 MPa，侧压力为2 MPa，即侧压力系数λ=0.2，计算出裂纹倾角从0°～90°之间的应力强度因子值。考察裂纹长度的影响时，设定λ=0.2，α=45°，进行计算，得出l的范围3.5 mm～15 mm之间的计算结果。而考察侧压力系数的影响时，设定圆心至裂尖的距离和竖直压力的值与前者相同，基于朱哲明等[11]对仅含单裂纹模型的复变函数理论解的结果，选取裂纹倾角为45°，以方便作为对照，计算出侧压力系数范围从0.0～2.0之间[8]两个裂尖处的应力强度因子。

2建模过程

按照上述模型尺寸，利用Abaqus软件，分别建立对应情况下的计算模型。设定材料类型为线弹性各向同性材料，弹性模量E=2.0 GPa，泊松比v=0.2，由于材料密度对于裂纹尖端的应力集中贡献很小，故可不设密度。

由于不考虑裂纹的宽度和后续扩展，即视为理想尖锐裂纹，使用Seam的方式定义两条裂纹及其尖端，并在裂尖处设定四分之一节点单元以产生应力奇异性。画网格时，对裂尖区域进行网格细化，从而获得较高的计算精度。具体为在裂尖设置6节点三角形CPS6单元，其余区域设置为8节点四边形CPS8单元。在45°倾角时右上角裂尖的网格放大图如图2所示。

图2裂尖的网格放大图

图2中，为了方便显示，将裂尖区域、积分区域、裂缝用橙色、红色标出。

对于边界条件，直接按照竖直压力和侧压力的大小，在上下表面和左右表面分别设置即可，不必设置位移边界条件。

3应力强度因子的计算原理

为了获得较高的计算精度，采用J积分的方式计算应力强度因子。具体思路为，预先在裂尖周围指定积分路径，程序根据路径计算J积分值。然后，两个应力强度因子KⅡ与KⅠ之间的比值RK可通过沿着裂纹上下表面某点的极坐标下的位移ux(r,θ)和uy(r,θ)表示：

(1)

其中，r0是从裂尖出发指向该点的很小的矢径。则应力强度因子为：

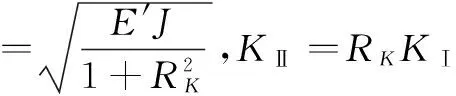
(2)

其中，E为杨氏模量，v为泊松比。

4模拟的结果

当考虑裂纹倾角的影响时，Abaqus软件的计算结果得出的KⅡ-α曲线如图3所示。对于压剪型裂纹，在不考虑裂纹扩展的情况下，Ⅰ型应力强度因子的计算结果为负值，所以这里没有讨论。

图3数值模拟的KⅡ-α曲线

图4数值模拟的KⅡ-l曲线

由图4可知，随着裂纹长度的增加，裂尖的Ⅱ型应力强度因子值明显增大。当l<8 mm时，裂尖A的应力强度因子值KⅡ要大于裂尖B，说明由于隧道构形的影响，裂尖A将可能先发生破坏；而当l≥8 mm时，二者的数值基本相同，表明当裂纹足够长时，隧道构形对裂纹的影响可以基本忽略不计，这也反过来表明此时裂纹将先于隧道发生一定的破坏或进一步的扩展。

考虑侧压力系数λ的影响时，由Abaqus软件模拟得出的隧道周边径向裂纹尖端应力强度因子KⅡ的走势图如图5所示。

图5数值模拟的KⅡ-λ曲线

5结论

由于实际工程地况的复杂性，需要研究隧道在穿过各种地形下的强度与稳定性，以及相应的应对措施。通过Abaqus软件对隧道穿越地裂缝或微断层的数值模拟，并得出以下结论：

(1) 直墙拱形隧道的共线径向双裂纹会降低隧道的强度及稳定性，且与裂纹倾角、裂纹长度和侧压力系数有关。

(2) 由于裂纹和隧道的非对称性，导致两个裂纹尖端的应力集中并不相同，在侧压力系数为0.2时，右上角和左下角裂尖的应力强度因子分别在倾角45°和52°时达到峰值；倾角53°前后，应分别优先考虑右上角和左下角裂尖处的安全问题。

(3) 随着裂纹长度的增加，隧道对两裂纹的应力强度因子的影响逐渐减弱。对于特定裂纹倾角、裂纹长度和侧压力系数下的隧道安全问题，应区别对待，不能一概而论。

(4) 为了进一步研究共线径向裂纹对隧道的强度及稳定性的影响，考虑增加模型试验和理论分析的方法，以相互印证。而关于两条裂纹的不同长度，隧道表面由于支护作用产生的法向压力等对隧道的影响也可进一步研究。

[1] 张志强,何本国,关宝树.节理岩体隧道围岩稳定性判定指标合理性研究[J].现代隧道技术,2012,49(1):12-19.

[2] CHARPENTIER D,TESSIER D,CATHELINEAU M.Shale microstructure evolution due to tunnel excavation after 100 years and impact of tectonic paleo-fracturing.Case of Tournemire,France[J].Engineering Geology,2003,70(1-2):55-69.

[3] 贾蓬,唐春安,杨天鸿,等.具有不同倾角层状结构面岩体中隧道稳定性数值分析[J].东北大学学报:自然科学版,2006,27(11):1275-1278.

[4] 晏启祥,程曦,杨征.断裂理论在含裂纹盾构隧道安全性评价中的应用[J].铁道标准设计,2010,53(6):94-96.

[5] 方秦,还毅,张亚栋,等.ABAQUS混凝土损伤塑性模型的静力性能分析[J].解放军理工大学学报:自然科学版,2007,8(3):254-260.

[6] 王蒙,朱哲明,曾利刚.巷道周边裂纹应力强度因子的实验研究[J].四川大学学报:工程科学版,2012,44(S1):99-103.

[7] 彭建兵,胡志平,门玉明,等.马蹄形隧道40°斜穿地裂缝的变形破坏机制试验研究[J].岩石力学与工程学报,2009,28(11):2258-2265.

[8] 李占海,朱万成,冯夏庭,等.侧压力系数对马蹄形隧道损伤破坏的影响研究[J].岩土力学,2010,31(S2):434-461.

[9] 范君黎,朱哲明,胡天立,等.高宽比对隧道围岩稳定性的影响[J].四川大学学报:工程科学版,2015,47(S1):76-83.

[10] 李元鑫,朱哲明,刘凯,等.裂纹方向对隧道稳定性影响规律的研究[J].岩土力学,2014,35(S1):189-194.

[11] ZHU Z M,WANG L,MOHANTY B,et al.Stress intensity factor for a cracked specimen under compression[J].Engineering Fracture Mechanics,2006,73(4):482-489.

[12] ZHU Z M.An alternative form of propagation criterion for two collinear cracks under compression[J].Mathematics and Mechanics of Solids,2009,14(8):727-746.

[13] ZHU Z M.Numerical prediction of crater blasting and bench blasting[J].International Journal of Rock mechanics and Mining Sciences,2009,46(6):1088-1096.

[14] ZHU Z M.New biaxial failure criterion for brittle materials in compression[J].Journal of Engineering Mechanics,1999,125(11):1251-1258.

[15] ZHENG T,ZHU Z M,WANG B,et al.Stress intensity factor for an infinite plane containing three collinear cracks under compression[J].Journal of Applied Mathematics and Mechanics,2014,94(10):853-861.

The Stress Intensity Factor for Two Collinear Cracks Emanated From Tunnel by Using Numerical Analysis

FUYangcheng,ZHUZheming,LIUkai,FANyong

(School of Architecture and Environment, Sichuan University, Chengdu 610065, China)

The complex rock mass structures around tunnel, such as jointing, ground fissures, will have negative influence of tunnel safety. By using Abaqus software, the tunnel under biaxial compression which goes through ground fissure is simulated. The crack inclinationα, crack lengthland lateral pressure coefficientλare analyzed for the influence of SIF and the stability of tunnel. The results show that: (1) crack inclination, crack length and lateral pressure coefficient have a great influence on SIF, and reduce the strength and stability of tunnel; (2) because of the shape of tunnel, the SIFs for upper and down crack tips reach the maximum whenαis 45° and 52° respectively, which means one should pay more attention to tunnel safety whenαis between 45° and 52° approximately. (3) the value ofλbetween 0.8 and 1.2 has a good effect on weakening stress concentration for crack tips, which is good for tunnel safety. (4) the crack effects on tunnel are the main consideration when the ratio of crack length to tunnel width is more than 5.

tunnel; collinear cracks; SIFs; strength; stability

2016-03-30

油气藏地质及开发工程国家重点实验室资助项目(PLN1202)

付杨成(1993-),男,安徽六安人,硕士生,主要从事断裂力学方面向的研究,(E-mail)753727362@qq.com;

朱哲明(1965-),男,教授,博士,主要从事断裂力学、冲击波与爆炸力学、计算力学等方面的研究,(E-mail)zhemingzhu@hotmail.com

1673-1549(2016)04-0059-05

10.11863/j.suse.2016.04.13

TB115

A