钢轨表面裂纹扩展路径的数值模拟

杨鸿达, 张言库, 李孝滔, 李煦, 江晓禹

(西南交通大学力学与工程学院, 成都610031)



钢轨表面裂纹扩展路径的数值模拟

杨鸿达, 张言库, 李孝滔, 李煦, 江晓禹

(西南交通大学力学与工程学院, 成都610031)

通过采用有限元分析软件ANSYS对钢轨表面裂纹扩展路径进行模拟，在主裂纹尖端微小区域虚设出不同角度的次裂纹来计算出钢轨表面斜裂纹的扩展路径。仿真结果表明模拟的裂纹路径与实验得到的裂纹路径基本吻合。由此可知，用虚设的次裂纹计算裂纹的扩展方向是可行的。

裂纹扩展；主裂纹；次裂纹；ANSYS

引言

由于高速铁路和重载铁路的快速发展，轮轨的损伤破坏问题已越来越普遍。我国每年因为钢轨的损伤维护甚至更换的费用达到了80亿，产生了高昂的铁路维护成本，这不仅加大了投入的成本，更直接威胁到列车的行驶安全[1]。例如，2002年，广深线曲线半径为1000 m的上股钢轨，先后有两处由踏面斜裂纹导致的钢轨横向断裂[2]。

国内外的学者对于复杂载荷作用下的裂纹扩展问题，采用的是在裂纹尖端建立一段相对于主裂纹无穷小的次裂纹，认为裂纹的扩展方向为：次裂纹KΙ最大方向，ΔKΙ最大的方向或者ΔKeff最大的方向等。很多研究者用这种方法来判断裂纹的扩展方向[3-8]。本文在主裂纹尖端区域虚设出不同方向的次裂纹，认为裂纹会朝等效应力强度因子幅值最大的方向扩展的判据，运用有限元软件ANSYS模拟计算出整条主裂纹的扩展路径，通过与实际钢轨裂纹形貌对比，结果基本吻合，验证了该方法的合理性。

1轮轨接触模型

陈朝阳等[9]测量统计了多组剥离掉块样品的裂纹扩展角度，得到裂纹的初始扩展角度大部分都在30°～65°之间。因此本次试验研究裂纹的初始扩展角度设为30°。模型如图1所示。

图1轮轨接触模型

2有限元模型

因我国铁路钢轨基本采用60 kg/m钢轨，其用材为U71Mn钢。U71Mn钢的力学性能[10]见表1。

表1U71Mn钢的力学性能

有限元模型高为176 mm、长为1 m、裂纹长度为100 μm，单元类型为奇异性单元PLANE183，钢轨整体有限元模型和裂纹尖端有限元模型如图2与图3所示。

图2表面含次裂纹的钢轨有限元模型

图3初始裂纹尖端的有限元模型

3结果分析

3.1裂纹扩展的速率

车轮在钢轨表面做纯滚动时，考虑主裂纹尖端微小区域的各个不同方向的次裂纹，可计算出各个不同方向上次裂纹的应力强度因子。

3k2sinθ0]

(1)

3k2sinθ0]

(2)

应力强度因子幅值：

ΔK=Kmax-Kmin

(3)

式中，ΔK决定了裂纹的扩展方向。裂纹扩展速率可根据Paris公式计算得到[12]：

(4)

由于轮轨接触疲劳裂纹是张开型与滑开型同时存在的复合型裂纹，所以不能由单一判据来作为断裂判断的依据，需根据复合型裂纹的判定依据，对于I型与II型同时存在的复合型裂纹，可用等效应力强度因子ΔKeff替代ΔKΙ与ΔKΙΙxXY共同作用效果[13]：

(5)

3.2通过次裂纹判断钢轨表面主裂纹扩展路径

研究车速为350 km/h，轴重为5 t的车轮在钢轨表面做纯滚动时，初始裂纹的角度为30°，长为100 μm。列车在钢轨表面运行时，钢轨在车轮的挤压效果下会使接触斑边缘附近的区域产生拉伸力，从而使次裂纹产生张开位移，在车轮接近裂纹位置及车轮滚过裂纹的某一位置时应力强度因子KΙ和KΙΙ的值均明显增大，出现两个峰值，如图4所示。其中x表示接触斑右边缘与裂纹端的距离。

图4车轮压过裂纹的过程中应力强度因子的变化

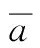
图5在主裂纹尖端建立的次裂纹模型

在初始裂纹尖端区域虚设出次裂纹，由公式(1)和公式(2)可计算得到车轮滚过斜裂纹的过程中，裂纹尖端假设的各个不同方向的次裂纹的应力强度因子，再通过公式(4)和公式(5)得到的次裂纹在各个方向的等效应力强度因子ΔKeff最大值，如图6所示。

图6虚设的次裂纹在不同方向的ΔKeff最大值

从图6中可看出，微裂纹在-10°时等效应力强度因子ΔKeff最大，最大值为23.4 MPa·m0.5，所以，主裂纹的下一段扩展方向为40°。之后每段方向都可依次得到，其主裂纹的扩展路径见表2。

表2主裂纹长度、扩展角度以及等效应力强度因子幅值最大值

为了更清楚地描述随着裂纹长度增加，主裂纹扩展趋势的变化情况，探究主裂纹的扩展规律，绘制出了不同长度时的主裂纹扩展速率最快的方向，如图7所示。从图7中可知，当裂纹长度a<0.6 mm时，主裂纹的扩展角度绕上一段顺时针旋转基本在15°左右，当裂纹长度a≥0.7 mm时，主裂纹基本沿着上一段方向继续扩展。

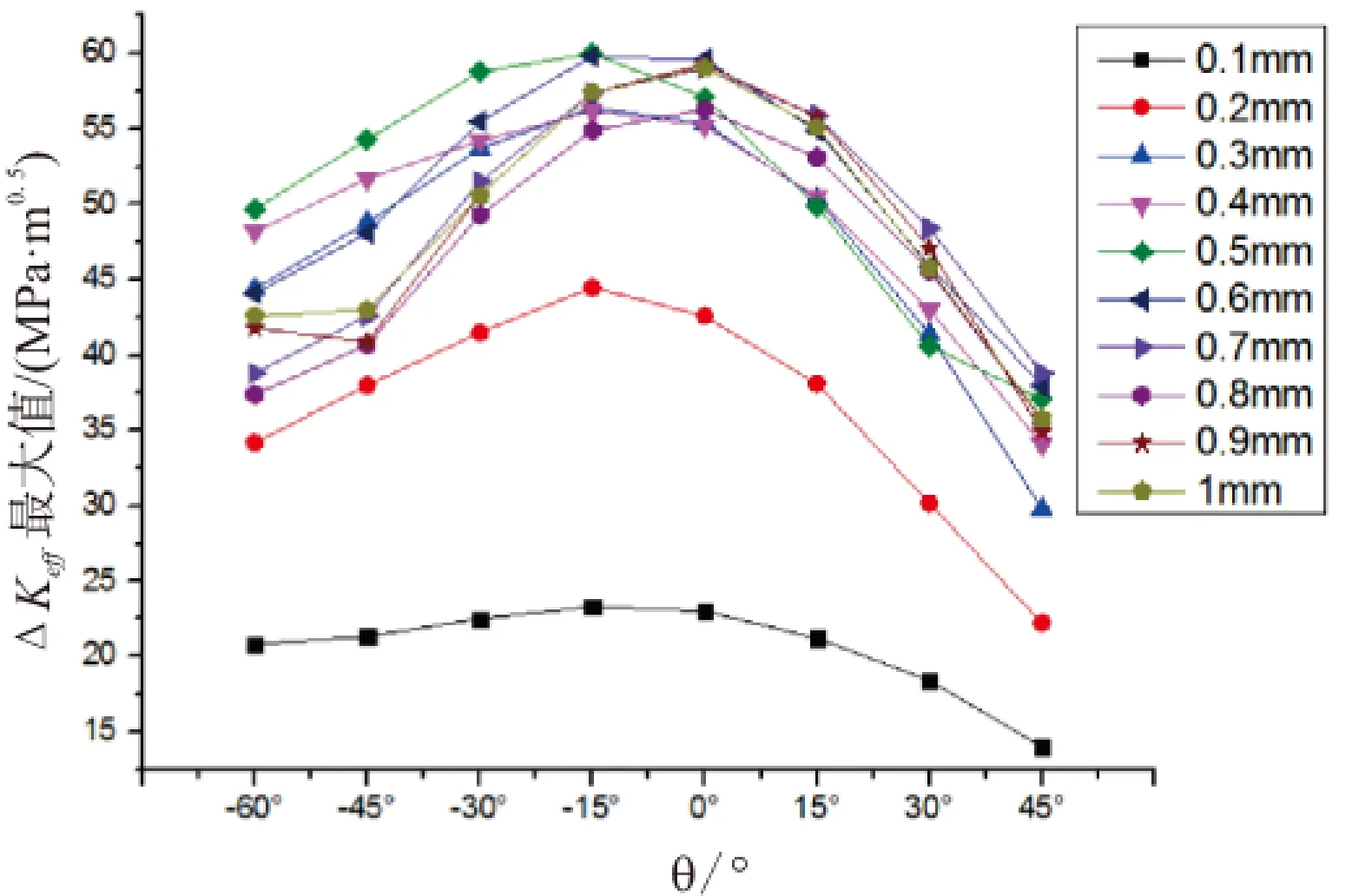
图7不同长度的次裂纹在各个方向上的最大扩展速率

综合表2与图7可知，每一段主裂纹扩展方向都比较平缓，没有出现较大幅度的波动。通过有限元数值模拟得到整条裂纹的扩展路径如图8所示。由图8可知，模拟结果与陈朝阳[9]等对朔黄线剥离掉块样品纵断面上的裂纹扩展路径的实物图片比较吻合。

图8模拟的裂纹扩展路径与实验测得的裂纹扩展路径对比

4结束语

本文研究U71Mn钢主裂纹的扩展路径，通过在主裂纹尖端微小区域虚设的次裂纹，并根据等效应力强度因子幅值最大的方向扩展的判据，通过有限元数值模拟了一条比较平滑的裂纹扩展路径，与实际得到的钢轨表面的裂纹扩展结果比较吻合，因此，通过次裂纹方向扩展的判据得出主裂纹扩展路径的方法是可行的。

[1] 金学松,温泽峰,张卫华,等.世界铁路发展状况及其关键力学问题[J].工程力学,2004,6(S1):90-102.

[2] 刘学文,邹定强,邢丽贤,等.钢轨踏面斜裂纹伤损原因及对策的研究[J].中国铁道科学,2004,25(2):82-87.

[3] DUBOURG M C,LAMACQ V.A predictive rolling contact fatigue crack growth model: onset of branching, direction, and growth-role of dry and lubricated conditions on crack patterns[J].Journal of Tribology,2002,124(4):680-688.

[4] HOURLIER F,PINEAU A.Propagation of fatigue crack under polymodal loading[J].Fatigue & Fracture of Engineering Materials & Structures,2007,5(4):287-302.

[5] BAIETTO M C,PIERRES E,GRAVOUIL A,et al.Fretting fatigue crack growth simulation based on a combined experimental and XFEM strategy[J].International Journal of Fatigue,2013,47:31-43.

[6] TROLLE B,BAIETTO M C,GRAVOUIL A,et al.2D fatigue crack propagation in rails taking into account actual plastic stresses[J].Engineering Fracture mechanics,2014,123:163-181.

[7] BROUZOULIS J,EKH M.Crack propagation in rails under rolling contact fatigue loading conditions based on material forces[J].International Journal of Fatigue,2012,45(3):98-105.

[8] BAIETTO M C,PIERRES E,GRAVOUIL A.A multi-model X-FEM strategy dedicated to frictional crack growth under cyclic fretting fatigue loadings[J].International Journal of Solids & Structures,2010,47(10):1405-1423.

[9] 陈朝阳,张银华,刘丰庆,等.朔黄铁路曲线下股热处理钢轨剥离损伤成因分析[J].中国铁道科学,2008,29(4):28-34.

[10] 何越磊,石嵘,刘志刚.城市轨道交通钢轨损伤检测技术[M].北京:中国铁道出版社,2010.

[11] NUISMER R J.An energy release rate criterion for mixed mode fracture[J].International Journal of Fracture,1975,11(2):245-250.

[12] PARIS P C,ERDOGAN F.A critical analysis of crack propagation laws[J].Journal of Basic Engineering,1963,85(4):528-534.

[13] LUCHT T.Finite element analysis of three dimensional crack growth by the use of a boundary element sub model[J].Engineering Fracture Mechanics,2009,76(14):2148-2162.

Numerical Simulation of Crack Propagation Path of Rail Surface

YANGHongda,ZHANGYanku,LIXiaotao,LIXu,JIANGXiaoyu

(School of Mechanics & Engineering, Southwest Jiaotong University, Chengdu 610031, China)

The finite element analysis software ANSYS is used to simulate the rail with surface crack growth. In the small region of the main crack tip, the crack of different angle is assumed to calculate the propagation path of the crack on the rail surface. As a result, the simulation of the crack path is basically consistent with the experimental crack path. In conclusion, it is reasonable to calculate the main crack propagation direction by dummy branch crack.

crack propagation; the main crack; the branch crack; ANSYS

2016-03-31

国家自然科学基金项目(11472230)

杨鸿达(1992-),男,湖南邵阳人,硕士生,主要从事疲劳与损伤方面的研究,(E-mail)2523047589@qq.com

1673-1549(2016)04-0012-04

10.11863/j.suse.2016.04.03

TB115

A