稀薄流高超声速飞行器气动加热耦合计算*

屈 程，王江峰

(南京航空航天大学 航空宇航学院， 江苏 南京 210016)



稀薄流高超声速飞行器气动加热耦合计算*

屈 程，王江峰

(南京航空航天大学 航空宇航学院， 江苏 南京 210016)

针对稀薄流域高超声速飞行器的气动加热问题，开展耦合数值计算研究。通过引入牛顿冷却定律，将直接模拟蒙特卡洛数值模拟方法与结构传热计算方法相结合，设计一种可对全机外形进行气动热和结构传热计算的高效松耦合方法，实现飞行器防热层结构材料温度分布特性的数值模拟。在以钝锥外形为例对直接模拟蒙特卡洛数值模拟程序进行验证的基础上，采用该方法对X37B轨道飞行器外形长时加热与结构传热过程进行数值模拟，给出结构温度及热流密度随飞行时间的变化规律。研究结果表明，设计的耦合计算方法能够模拟稀薄流域高超声速飞行器的气动加热及结构传热耦合过程，可为该类飞行器的气动热分析及热防护设计提供技术支持。

稀薄流；高超声速；气动热；结构传热；牛顿冷却定律；直接模拟蒙特卡洛；松耦合

随着各国军事综合实力的提升，新型战略导弹、先进型诱饵和跨流域飞行器得到了进一步发展，由于此类飞行器的峰值加热区都处于60～80 km高空的稀薄流区，因而稀薄流域高超声速飞行器的气动加热问题越来越受到人们的重视，精确预测高超声速飞行器在稀薄流域的气动加热以及结构在气动加热作用下的温度变化特性能够为此类飞行器的结构强度计算和热应力计算提供初始计算依据，而这对于稀薄流域高超声速飞行器的气动特性及热防护设计具有十分重要的意义。

目前在连续流域，对高超声速飞行器气动加热耦合数值计算方面的研究发展已相对较成熟[1-3]。然而在稀薄流域，对于气动热方面的数值模拟研究还主要集中于飞行器的气动热环境模拟以及气动热环境影响因素方面[4-6]，关于稀薄流域高超声速飞行器气动热与结构传热耦合数值计算方面的研究还较为少见。

1 计算方法

1.1 DSMC方法介绍

直接模拟蒙特卡洛(Direct Simulation Monte Carlo,DSMC)方法是求解稀薄气体动力学问题最为成功的数值方法之一[7-8]，该方法使用大量的模拟分子模拟真实的气体，用一个模拟分子代表一定数量的真实气体分子，该方法的本质是在时间步长Δt内，对分子的运动和分子间的碰撞进行解耦。整个模拟过程中分子之间以及分子和物面之间不断进行能量交换，在经历充足的模拟时长后，通过采样统计得到每个网格的宏观流场结果。DSMC方法中，计算网格起两种作用[9]：第一种是对流场宏观流动参数进行空间离散；第二种是促进碰撞分子碰撞对的选择，使其满足基本的几何接近。计算中采用可变硬球(Variable Hard Sphere, VHS)分子模型，利用Bird非时间计数器(No Time Countor, NTC)法进行碰撞对的选取，使用Larsen-Borgnakke唯象论模型处理模拟分子间的能量交换[10]。

1.2 物面气动加热热流及传热系数

在DSMC方法中，飞行器物面的气动特性是根据入射分子及反射分子数通量、动量通量以及能量通量进行计算的。为了保证DSMC方法描述复杂外形气动热的准确性，在数值模拟中采用对复杂外形适应性较强的非结构贴体网格；利用模拟分子与相邻单元面的相交理论设计分子搜索算法，该搜索算法能够准确跟踪分子在网格之间的迁移并给出分子与物面作用的精确时间与确切位置；同时，在选择分子碰撞对时引入碰撞距离的思想，这样处理能够在放宽DSMC方法对网格尺度要求的情况下保证计算精度。

仅考虑对流传热，作用在飞行器物面的气动加热热流qw可表示为单位时间内单位面积上入射分子与反射分子的总能量之差：

(1)

牛顿冷却定律是传热学的基本定律之一，主要是为解决气体与固体之间的对流热交换给出的，牛顿冷却定律没有考虑物体的性质，而是从数学的角度给出了热流密度与温度差值之间的关系，因此，通常也将牛顿冷却定律称为“牛顿冷却定理”。根据牛顿冷却定律，当物体表面温度与附近气体温度存在温度差时，物面热流密度可以表示为：

(2)

式中，α为传热系数，Tf为物面附近气体温度，Tw为物面温度，热流方向由高温指向低温。

当飞行器以高超声速在稀薄流中飞行时，前方空气受到弓形激波强烈压缩，在与飞行器表面的剧烈摩擦作用下，巨大的动能转换成空气热能，高温空气与飞行器表面之间存在较大的温差[11-12]，满足牛顿冷却定律的使用条件，因此，高超声速稀薄流场中飞行器物面的气动加热热流也可以表示为:

qw=α(Tf-Tw)

(3)

联系式(1)和式(3)，传热系数α可以表示为：

(4)

1.3 结构传热计算

为了保证较高的计算效率，防热层结构温度分布由一维热传导方程构建差分方程求解，根据防热层毕奥数的大小，防热层分为热薄壁和热厚壁，两者分别采用不同的传热计算公式[13]。其中，热薄壁传热公式表述为：

(5)

(6)

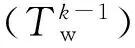
(7)

Δt=t-tk-1

(8)

其中，k为当前时间步，传热系数α由式(4)求得，初始条件为式(6)。

本文结构传热计算方法为课题组现有技术基础(课题组发展的连续流域“高速飞行器气动加热计算与分析”软件已在相关航空航天型号设计单位得到了成功应用)，求解过程需要换热系数及物面附近气体温度。采用DSMC计算方法能够得到物面气动加热热流密度及物面附近气体温度，不能直接得到换热系数。本文引入牛顿冷却定律，实现了换热系数的求解，从而实现了稀薄流域DSMC气动热计算方法与现有结构传热计算方法的结合。

1.4 稀薄流气动热与结构传热耦合方法

流场与结构传热的耦合计算方法可以分为紧耦合方法和松耦合方法两类[14-15]。紧耦合方法是指流场与结构传热按照统一流场特征时间步长求解，该方法的特点是流场与结构传热实时耦合，反映了物理实际，但是计算需要消耗较长的计算时间；松耦合方法假定流场特征时间很小，相比于结构传热的特征时间，认为流场是瞬态稳定的，因此可以采用结构计算的特征时间或者是更长的人为给定的时间作为耦合计算的特征时间步长，在这一特征时间内认为流场是瞬时稳定的。和紧耦合方法相比，松耦合方法能够在保证一定计算精度的前提下具有紧耦合方法无法比拟的计算效率。

考虑到稀薄流DSMC方法本身计算效率较低，进行高超声速稀薄流气动热与结构传热耦合计算时采用了效率较高的松耦合方法，耦合步骤设计如下：

1)给定t=0时刻物面的温度分布，通过DSMC方法进行高超声速稀薄流流场计算得到物面上的气动加热热流分布；

2)假定步骤1中求得的气动加热热流分布在耦合时间步Δt内保持不变，通过结构传热计算得到该时间步内结构温度场的变化过程；

3)根据步骤2中求得的物面温度分布再通过DSMC流场计算得到新时刻的物面气动加热热流分布；

4)回到步骤2，不断循环迭代，直至计算要求的截止时刻。

2 钝锥外形算例验证

对钝锥外形高超声速稀薄流绕流进行了计算，模型尺寸如图1所示，头部半径R=35 mm，半锥角为5°。来流气体为空气，飞行高度为90 km，来流密度为3.416×10-6kg/m3，温度为181 K,来流速度为5000 m/s，攻角为0°，物面温度为300 K，全场四面体网格单元数为132 875，流场模拟分子总数趋于稳定后约为183万。

图2和图3分别给出了气动加热热流密度和物面压力分布云图。观察图2和图3可以看出气动加热热流密度和压力峰值出现在驻点区域，锥面整体热流密度和压力相对较低。图4(a)和图4(b)分别给出了物面气动加热热流密度和压力分布与文献[16]计算结果的对比，观察图4可以发现本文计算结果与文献值符合较好。

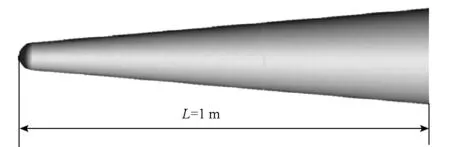
图1 钝锥示意图Fig.1 Blunted cone

图2 物面气动加热热流密度分布云图Fig.2 Distribution of surface heat flux

图3 物面压力分布云图Fig.3 Distribution of surface pressure

3 X37B外形长时加热算例

由于缺乏类似算例对比，本文针对X37B轨道飞行器外形，人为设定了一个定速长时飞行状态及热防护方案，并采用上述所设计的方法进行气动加热计算。飞行条件为：攻角0°，飞行高度80 km，来流气体为空气，温度为198 K，来流密度为1.846×10-5kg/m3，来流速度为5000 m/s，飞行时间100 s，初始物面温度为300 K，热防护方案如表1所示，计算模型长约0.82 m，头部曲率半径约为0.02 m，基于头部曲率半径的努森数约为0.22，计算区域及物面网格如图5所示，四面体网格单元数为988 175。

(a) 热流密度(a) Heat flux

(b) 压力(b) Pressure图4 物面气动参数分布Fig.4 Aerodynamic parameters on the surface

表1 热防护类型和材料设置

(a) 计算区域(a) Calculation domain boundary

(b) 表面网格(b) Surface grids图5 X37B外形计算区域及表面网格Fig.5 Calculation domain boundary for X37B shape and surface grids

DSMC方法一般以统计涨落的情况作为判断收敛的标准，根据统计原理，随机系统的统计涨落仅依赖于模拟分子总数，当流场模拟分子总数趋于稳定时认为计算收敛。本算例单状态流场计算程序迭代100 000步，在模拟分子总数趋于稳定后并未结束计算，而是进行了更多次的迭代，使得有足够的统计样本数来保证气动热计算结果的可靠性。

采用稀薄流DSMC方法模拟复杂三维流动问题计算量较大，串行计算耗时代价较高，为提高计算效率，采用主从(master/slave)并行模式DSMC数值模拟程序，通过保证各子区域的分子数量大致相等实现计算进程的动态负载平衡[17]。采用的是分布式共享内存并行体系结构PC-CLUSTER机群系统，硬件环境为：28子节点，每个子节点包含16个Intel®Xeon®E5-2660 2.40GHz CPU，共享32 GB内存，Infiniband宽带。本算例采用32个CPU计算，单状态流场模拟分子总数趋于稳定后约为1036万，计算约耗时9 h。

图6给出了初始时刻流场计算得到的气动参数分布等值线及云图。图6(a)为密度分布等值线及云图，观察图6(a)可以看出迎风区激波后气体密度增加，在驻点处密度达到最大；图6(b)为速度分布等值线及云图，观察图6(b)可以看出经过激波之后气流速度开始降低，在驻点处速度降至最低；图6(c)为平动温度分布等值线及云图，观察图6(c)可以发现激波后的平动温度显著增大，由于受等温物面边界的影响，在驻点附近又出现了降低。

(a) 密度(a) Density

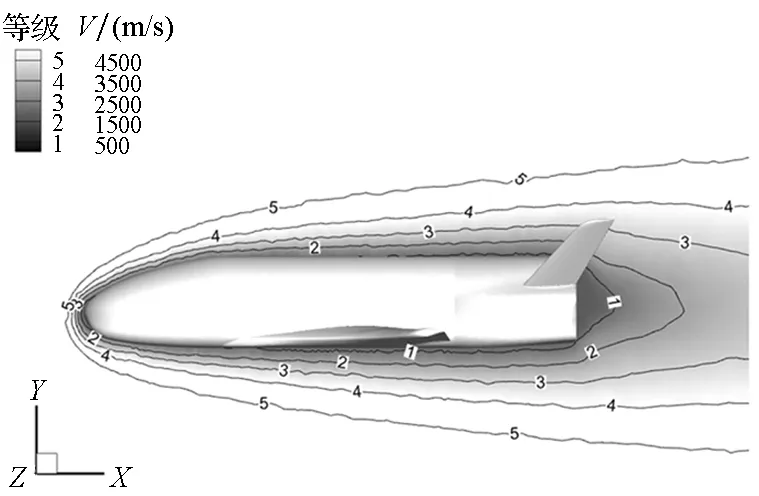
(b) 速度(b) Velocity

(c) 平动温度(c) Translational temperature图6 初始时刻流场参数分布等值线及云图Fig.6 Contours of flow field parameter at the initial time

图7给出了初始时刻流场计算得到的外表面气动加热热流密度云图，观察图7可以看出热流密度峰值出现在驻点、机翼翼梢前缘及尾翼翼梢前缘位置，并且，从图中可以看出机翼翼梢前缘位置的热流密度高于飞行器头部驻点处，这主要是因为：机翼翼梢前缘处的曲率半径小于头部驻点处，相对而言热量更易集中；同时，在头部形成的激波没有包住机翼翼梢。外表面其他位置的热流密度相对较低。

图7 初始时刻外表面气动加热热流密度分布Fig.7 Distribution of outer surface heat flux at the initial time

图8给出了不同时刻外表面温度分布云图，观察图8(a)～(h)可以发现，飞行过程中外表面温度升高非常显著。在流场气动加热的作用下，前30 s外表面温度上升较快，之后温度上升开始变缓，这主要是由于从外表面辐射出的热流密度正比于温度的四次方，初始外表面温度较低，辐射热流密度较小，传入结构的热流密度较高，因此外表面温度上升迅速，但是随着外表面温度的不断提升，从外表面辐射出的热流密度越来越大，使得传入结构中的热流密度越来越低，致使外表面温度上升变缓。

图9给出了t=100 s时刻防热层内表面温度分布云图，可以发现内表面温度和图8(h)中t=100 s时刻外表面温度的差别非常显著，这表明本文设定的热防护方案能够起到有效的热量隔绝作用。

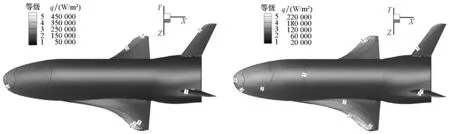
图10给出了不同时刻结构传热热流密度分布云图，观察图10(a)～(h)可以发现，初始结构传热量较高，随时间推移，前30 s结构传热热流密度下降较快，之后结构传热热流密度下降变缓。可以预测，随着时间继续推进，在气动加热的作用下，从外表面辐射出的热流密度与气动加热热流密度会越来越接近，外表面将趋于辐射平衡的状态。

本算例结构传热计算过程在一台配置为Intel®CoreTM2 2.80GHz，2.00GBRAM的微机上进行，计算时间约10 min(不记DSMC程序计算时间)，由此可知本文设计的稀薄流气动加热耦合计算方法能够对全机外形气动加热过程进行相对较高效率的计算与分析。

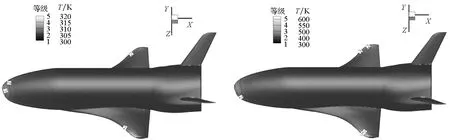
(a) t=0.05 s (b) t=1 s

(c) t=5 s (d) t=10 s

(e) t=20 s (f) t=30 s

(g) t=60 s (h) t=100 s图8 不同时刻外表面温度分布Fig.8 Distribution of outer surface temperature

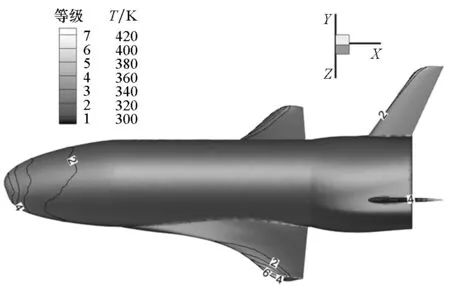
图9 t=100 s时刻内表面温度分布Fig.9 Distribution of internal surface temperature (t=100s)

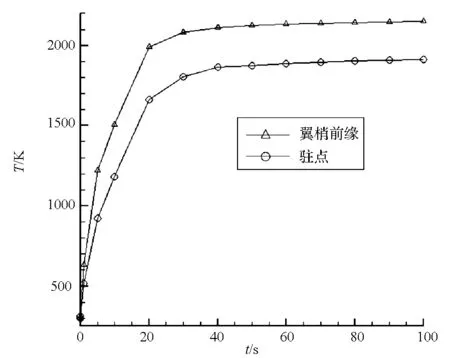
图11给出了不同时刻外表面驻点和机翼翼梢前缘的结构传热热流密度数值。观察图11可以发现外表面驻点结构传热热流密度在前30 s下降较快，从836 kW/m2下降到了217 kW/m2，在30 s后下降速度变缓，机翼翼梢前缘结构传热热流密度高于驻点位置，但是随时间变化趋势与驻点位置基本一致，同样在前30 s下降较快，从1299 kW/m2下降到了235 kW/m2，而在30 s后下降速度变缓。图11中外表面驻点和机翼翼梢前缘的结构传热热流密度随时间变化的规律与前文分析相符。

(a) t=0.05 s (b) t=1 s

(c) t=5 s (d) t=10 s

(e) t=20 s (f) t=30 s

(g) t=60 s (h) t=100 s图10 不同时刻结构传热热流分布Fig.10 Distribution of structure heat flux

图11 不同时刻外表面特征位置结构传热热流密度Fig.11 Structure heat flux on the outer surface characteristic position

(a) 外表面(a) Outside surface

(b) 内表面(b) Internal surface图12 不同时刻特征位置温度Fig.12 Temperature on the characteristic position

图12给出了不同时刻驻点和机翼翼梢前缘的温度数值。观察图12(a)可以发现外表面驻点和机翼翼梢前缘温度在前30 s上升较快，相同时刻机翼翼梢前缘温度比驻点处高，这是因为初始时刻结构温度都为300 K，在前30 s同一时刻机翼翼梢前缘处的结构传热热流密度都高于驻点处，因此机翼翼梢前缘处温度升高比驻点处更快。虽然30 s后机翼翼梢前缘处与驻点处的结构传热热流密度差别越来越小，但是机翼翼梢前缘温度依然高于驻点处。另外，在30 s后机翼翼梢前缘处与驻点处的温度上升速度均变缓。观察图12(b)可以发现驻点和机翼翼梢前缘防热层内表面温度在前40 s基本没有升高，在40 s后温度升高加快，但与图12(a)中同时刻对应位置外表面温度相比，仍然较低。

4 结论

通过引入牛顿冷却定律，将高超声速稀薄流域气动热DSMC数值模拟方法与课题组现有结构传热计算方法相结合，设计了一种可适用于全机外形复杂流场的高超声速稀薄流气动加热松耦合计算方法，主要结论如下：

1) 钝锥外形验证算例表明本文DSMC数值模拟程序能够正确模拟稀薄流域高超声速飞行器表面的气动热分布；

2) X37B外形长时加热算例给出了不同时刻结构温度及热流密度分布特性，从温度和热流密度分布云图可以看出非常显著的气动加热现象，热防护设计能够有效隔绝热量向飞行器结构内部的传递，该算例同时也表明所设计的气动加热耦合计算方法具有一定可行性，能够用于模拟全机外形下的高超声速稀薄流气动加热问题。

在本文的研究中，没有考虑稀薄空气中化学反应效应对气动加热过程的影响，对此，将做更进一步的研究。

References)

[1] Hamilton H H, Weilmuenster K J, Dejarnette F R. Approximate method for computing laminar and turbulent convective heating on hypersonic vehicles using unstructured grids[C]//Proceedings of 41st AIAA Thermophysics Conference, AIAA 2009-4310, 2009.

[2] Zhao J S, Gu L X, Ma H Z. A rapid approach to convective aeroheating prediction of hypersonic vehicles[J]. Science China Technological Sciences, 2013, 56(8): 2010-2024．

[3] Prakash A, Zhong X. Numerical simulation of planetary reentry aeroheating over blunt bodies with non-equilibrium reacting flow and surface reactions[C]//Proceeding of the 47th AIAA Aerospace Sciences Meeting including the New Horizons Forum and Aerospace Exposition, AIAA 2009-1542, 2009.

[4] 黄飞, 张亮, 程晓丽, 等.稀薄气体效应对尖前缘气动热特性的影响研究[J].宇航学报, 2012, 33(2): 153-159.

HUANG Fei, ZHANG Liang, CHENG Xiaoli, et al. Effects of continuum breakdown on aerothermodymics [J].Journal of Astronautics, 2012, 33(2): 153-159.(in Chinese)

[5] 屈程, 王江峰.DSMC算法气体壁面相互作用模型[J]. 南京航空航天大学学报, 2015, 47(3): 348-354.

QU Cheng, WANG Jiangfeng. Gas-surface interaction models for DSMC method[J].Journal of Nanjing University of Aeronautics & Astronautics, 2015, 47(3): 348-354. (in Chinese)

[6] Qu C, Wang J F. Hybrid grid DSMC method for chemical nonequilibrium with rarefied flow heating[J].Transactions of Nanjing University of Aeronautics and Astronautics, 2015, 32(4): 408-414.

[7] Boyd I D. Computation of hypersonic flows using the direct simulation Monte Carlo method[J]. Journal of Spacecraft & Rockets, 2015, 52(1): 38-53.

[8] 樊菁. 稀薄气体动力学：进展与应用[J].力学进展， 2013, 43(2): 185-201.FAN Jing. Rarefied gas dynamics: advances and applications[J]. Advances in Mechanics， 2013, 43(2): 185-201.(in Chinese)

[9] Gallis M A, Torczynski J R, Rader D J, et al. Convergence behavior of a new DSMC algorithm[J]. Journal of Computational Physics, 2009, 228(12): 4532-4548.

[10] Bird G A. Molecular gas dynamics and the direct simulation of gas flow[M].USA: Clarendon Press, 1994.

[11] Brykina I G, Perunov M V, Rogov B V, et al. About bounds of applicability of continuum approach to the problems of hypersonic rarefied flow over bodies[C]//Proceedings of West-East High Speed Flow Field Conference, 2007.

[12] Tseng K C, Wu J S, Boyd I D. Simulations of re-entry vehicles by using DSMC with chemical-reaction module[C]//Proceedings of 14th AIAA/AHI Space Planes and Hypersonic Systems and Technologies Conference,AIAA 2006-7917, 2006.

[13] 季卫栋, 王江峰, 唐国庆.高超声速多体分离过程气动加热计算技术[J]. 空气动力学报， 2014, 32(6): 761-766.

JI Weidong, WANG Jiangfeng, TANG Guoqing. Calculating method of aerodynamic heating for hypersonic multi-body seperation process[J]. Acta Aerodynamica Sinica, 2014, 32(6): 761-766. (in Chinese)

[14] Ramon C, Houzeaux G. Numerical approximation of the heat transfer between domains separated by thin walls[J]. International Journal for Numerical Methods in Fluids, 2006, 52(9): 963-986.

[15] Ji W D, Wang J F. Calculating method of aerodynamic heating for hypersonic aircrafts[J]. Transactions of Nanjing University of Aeronautics and Astronautics, 2013,30(3): 237-242.

[16] 黄飞， 陈智， 程晓丽， 等. 一种基于自适应碰撞距离的DSMC虚拟子网格方法[J]. 空气动力学报, 2014, 32(4): 506-510.

HUANG Fei, CHEN Zhi, CHENG Xiaoli, et al. A virtual sub-cells technique with transient adaptive collision distance for the DSMC method[J]. Acta Aerodynamica Sinica, 2014, 32(4): 506-510. (in Chinese)

[17] 王学德. 高超声速稀薄气流非结构网格DSMC及并行算法研究[D].南京:南京航空航天大学， 2006.

WANG Xuede. DSMC method on unstructured grids for hypersonic rarefied gas flow and its parallelization [D].Nanjing:Nanjing University of Aeronautics and Astronautics, 2006.(in Chinese)

Coupled calculation of aerodynamic heating for hypersonic vehicle in rarefied flow

QU Cheng, WANG Jiangfeng

(College of Aerospace Engineering, Nanjing University of Aeronautics and Astronautics, Nanjing 210016, China)

A coupling method was presented to deal with the heating problems of hypersonic vehicles in rarefied flow. The DSMC (direct simulation Monte Carlo) method was combined with the heat conduction equation by introducing the Newton cooling law. An efficient loose coupling procedure which can calculate the aerodynamic heat and structure heating of vehicle configuration was designed to simulate the temperature distribution of thermal protection systems. After taking the blunted cone as an example to validate the DSMC code, a numerical experiment was conducted to simulate the structure temperature and heat flux distribution characteristics of the X37B orbital vehicle shape in cruise state. The results show that the presented coupling method can simulate the aerodynamic heating process of a hypersonic vehicle in rarefied flow, and can provide technical support for the design of rarefied-flow hypersonic vehicles in terms of thermal protection systems and aerodynamic heating characteristics analysis.

rarefied flow; hypersonic; aerodynamic heat; structure heating; Newton cooling law; direct simulation Monte Carlo; loose coupling

10.11887/j.cn.201605018

http://journal.nudt.edu.cn

2015-11-13

屈程(1988—)，男，江苏泰兴人，博士研究生，E-mail：nuaaqu@163.com；王江峰(通信作者)，男，教授，博士，博士生导师，E-mail：wangjf@nuaa.edu.cn

V19,V211

A

1001-2486(2016)05-112-09