高超声速滑翔飞行器变轨段自适应跟踪制导方法*

何睿智，刘鲁华，汤国建，包为民,2

(1.国防科技大学 航天科学与工程学院， 湖南 长沙 410073； 2.中国航天科技集团公司， 北京 100048)



高超声速滑翔飞行器变轨段自适应跟踪制导方法*

何睿智1，刘鲁华1，汤国建1，包为民1,2

(1.国防科技大学 航天科学与工程学院， 湖南 长沙 410073； 2.中国航天科技集团公司， 北京 100048)

针对高超声速滑翔飞行器变轨段大偏差条件下的标准轨迹跟踪问题，提出一种基于权值矩阵自适应修正的变轨段跟踪制导方法。分析了变轨段主要控制方式和标准轨迹特性；将简化的纵向运动方程在标准轨迹附近线性化；采用将误差项引进线性二次型性能指标加权矩阵的方式，设计了改进的权值自适应修正跟踪制导方法。CAV-H飞行器仿真分析表明，该方法能够实现高超声速滑翔飞行器变轨段高精度自适应跟踪制导，对初始及过程偏差具有良好的鲁棒性。

高超声速滑翔飞行器；变轨段；权值矩阵修正；自适应跟踪制导

高超声速滑翔飞行器是一种飞行速度超过5马赫，具有大升阻比气动外形的无动力飞行器，它具有高速度、远航程、强机动性等特点。发展高超声速滑翔飞行器技术对于增强国防实力，维护国家安全，具有重要的战略意义。

变轨段又称作引入段[1]，是高超声速滑翔飞行器全程弹道中较为特殊的飞行阶段。该飞行阶段连接初始再入点和滑翔起点，使得飞行器在满足热流约束条件的前提下，顺利过渡到滑翔段，起到初期的调整作用。该阶段飞行高度大，大气密度小，飞行器控制调整能力较弱，进一步，由于该飞行阶段所处环境的特殊性，大气密度、气动力参数偏差往往较大，在大偏差强不确定性条件下的弹道设计和制导方法研究是飞行器系统设计中的一大难点。

标准轨迹跟踪制导[2-4]即依赖于标准轨迹，选择合适的状态反馈量进行控制量调整，实现对偏差的修正，最终完成标准轨迹跟踪飞行。标准轨迹可理解为广义的标准轨迹，既包含实际的三维飞行轨迹[5]，也包含例如D-V[6]、H-V[7]等剖面形式标准轨迹。标准轨迹跟踪制导包括两部分研究内容：一是标准轨迹的生成；二是跟踪方法的选择。标准轨迹生成中通常考虑多种约束条件，寻找某性能指标最优[8]的标准轨迹提供给跟踪系统，而跟踪系统主要考虑的是快速性和收敛性。通常采用的标准轨迹跟踪制导方法都是在小偏差假设条件下进行线性化[9-10]，利用线性系统相关理论进行最优化跟踪，包括能量最优、时间最短等。在众多针对多目标优化跟踪制导方法中，存在一个共性的问题，即如何选取合适的加权值进行能力的合理分配。通常采取人为参数设置的方式，例如典型的Bryson选取原则[11]；但是，一套设定好的参数很难适应不同偏差条件下的跟踪制导需求。如何提高参数选取的自适应能力是设计的关键性技术问题。

本文提出了一种利用误差反馈进行权值修正的改进线性二次型调节自适应跟踪制导方法。该方法以终端能量为优化指标，将状态偏差项以修正量形式反馈到跟踪制导性能指标权值矩阵中，通过自适应调整最优跟踪性能指标参数，间接调节跟踪制导中的增益，从而更好地对状态偏差进行自适应修正，具有更强的自适应调整能力。

1 运动建模及标准轨迹设计

1.1 运动方程

考虑地球为旋转圆球，无量纲运动方程为：

(1)

其中：r为飞行器质心距地心的径向距离；θ和φ分别为飞行器所处经度和纬度；V为相对地速；γ为航迹倾角，是速度矢量与当地水平面之间的夹角，在上为正；ψ为航向角，是当地经度线与速度在水平面上的投影线之间的夹角，顺时针为正；L和D分别为升力加速度和阻力加速度；σ为倾侧角。

由于运动方程组中各变量值数量级相差较大，这在进行数值计算时是极其不稳定的因素，因此，为了提高仿真精度、增强算法收敛性，已将上述方程组进行归一化处理。

1.2 约束条件

变轨段轨迹设计中需要考虑的约束条件包括过程约束、终端约束以及控制量约束。

1.2.1 过程约束

考虑到飞行器热防护需求以及自身负载特性限制，需要对驻点热流密度、动压和过载峰值进行限制。

(2)其中：驻点热流密度为变轨段过程约束考虑的主要项，而动压及过载峰值则通常较小；KQ为常数，其取值与飞行器相关，现取为5×10-5；m取3.15。

1.2.2 终端约束

变轨段终端约束条件为满足起滑点要求，即

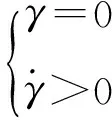
(3)

由于变轨段终端高度直接影响到后续高超声速滑翔段条件，因此高度通常也作为滑翔段终端约束条件之一。

h=h*

(4)

其中，h*为变轨段终端设计高度值。

1.2.3 控制量约束

倾斜转弯(Bank To Turn, BTT)模式下滑翔飞行器控制量为攻角和倾侧角，其幅值及变化率均应在一定范围内。

(5)

1.3 标准轨迹设计

如图1所示，变轨段标准轨迹设计即获得合适的飞行程序角使得飞行器从起始点平缓过渡到滑翔接口点，且满足过程约束、终端约束及控制量约束。

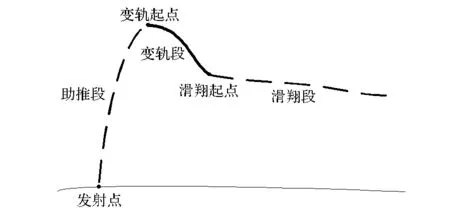
图1 变轨段示意图Fig.1 Diagram of injection phase

变轨段飞行高度通常在60～100 km，大气密度稀薄，气动调整能力较弱，不适宜对侧向进行大范围调整。因此，考虑将该阶段飞行控制模式设计为定攻角剖面和常值倾侧角控制模式，如图2所示。

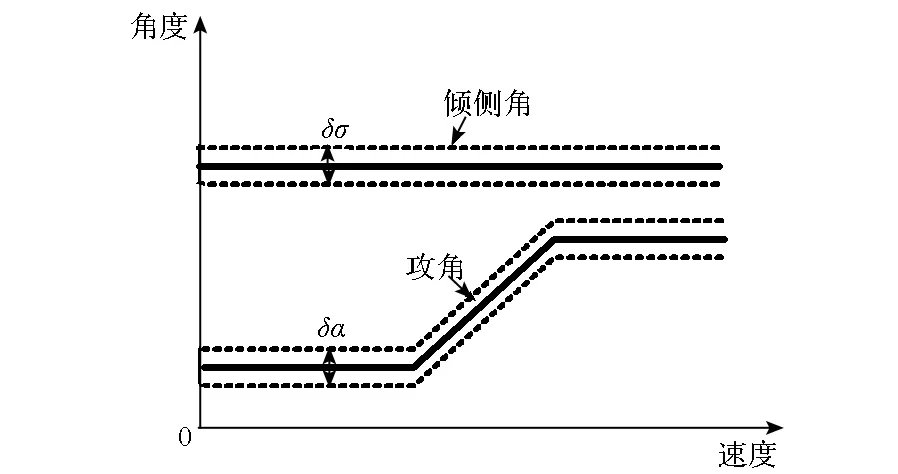
图2 标准轨迹控制量形式Fig.2 Controlled variable of standard trajectory

变轨段控制量选取形式较为简单，但其具体参数数值需要根据飞行任务进行快速计算，整个设计计算流程如图3所示。

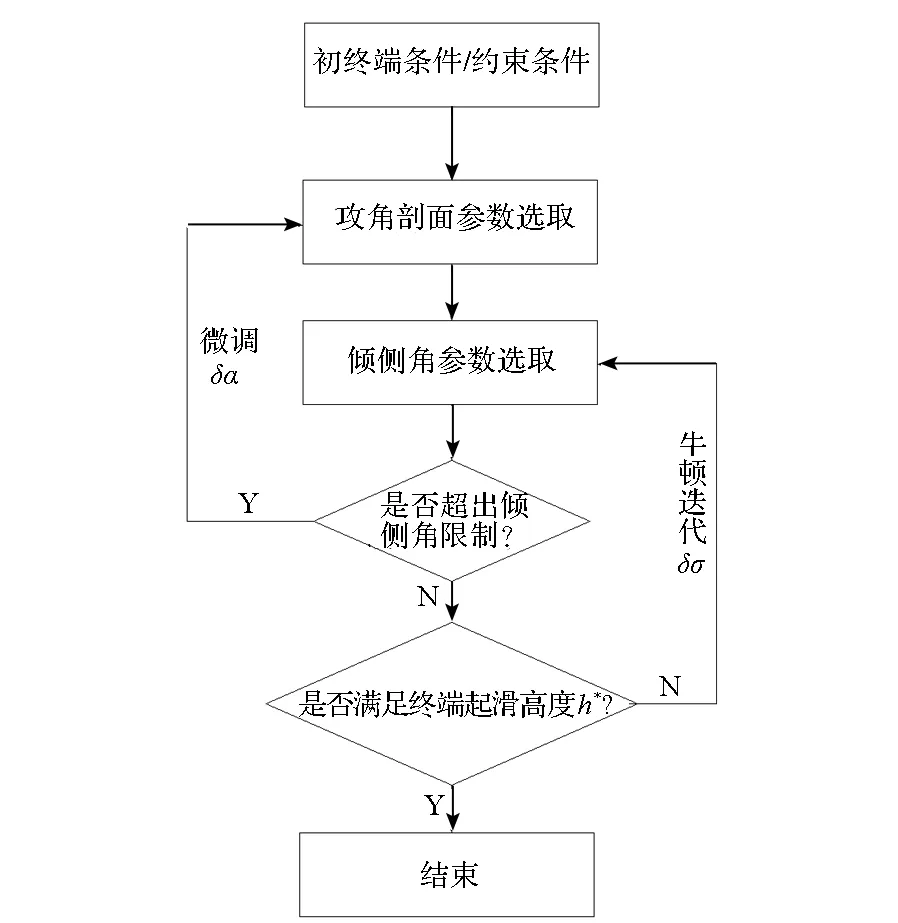
图3 控制量设计流程图Fig.3 Design cycle diagram of controlled variable

首先设计攻角剖面，将其选取为速度的分段线性函数，在高速段采用大攻角飞行，低速段采用小攻角飞行，以满足热流密度约束条件，保证飞行过程中热防护系统工作正常。

以终端滑翔起点要求为仿真终止条件，采用牛顿迭代法对常值倾侧角迭代，获得满足起滑点终端高度要求的变轨段标准轨迹。

2 自适应最优跟踪制导

2.1 方程线性化

不考虑地球自转，并假设地球为均质圆球，简化的纵平面动力学方程为：

(6)

其中，阻力加速度、升力加速度以及大气密度可分别表示为：

(7)

其中，hs=7110 m，ρ0=1.225 kg/m3。

为方便在方程线性化过程中对气动参数导数的处理，将气动参数CD,CL拟合为多项式形式[11]。

(8)

对纵向运动方程在标准轨迹附近线性化。

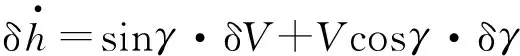
其中，

(9)

(10)

该线性化过程会引入一定的模型误差，但当飞行器状态在标准状态附近时，该模型误差为小量。在后续的跟踪制导中，整个系统为闭环误差修正系统，可以保证飞行过程状态偏差逐渐收敛至零。

2.2 线性二次型调节器设计

(11)

其中

(12)

(13)

(14)

为了实现对标准轨迹的跟踪，使δx趋于0，可以作为线性二次型调节问题(Linear Quadratic Regulator ,LQR)求解，取标准的线性二次型性能指标为：

(15)

其中，Q和R称为性能指标加权阵，为对角阵，其值的不同将直接影响跟踪系统性能。由表达式可以直观看出，Q与跟踪精度直接相关，一般来讲取值越大精度越高；R与控制量直接相关，取值越大控制量越省。

(16)

传统的Bryson选取原则[12]为：

(17)

考虑到这种直接的固定参数选取方式，往往带来对不同偏差条件的自适应调整能力弱等问题，为了将权值矩阵的选取直接与期望的直观要求建立联系，同时考虑适应于不同的偏差条件，将偏差项以一定的形式进行反馈，提出如式(18)所示性能指标加权矩阵形式，以速度项权值Q2为例。

(18)

a为常值项，通过该常值项的设置，保证跟踪制导系统的稳定性，即当飞行过程中状态量偏差δv为零时，常值项a的存在，保证线性二次型性能指标权值矩阵中与V相关的对角元素值Q2非零。进一步，考虑到δVmax为设置的允许误差最大值，系统状态偏差通常小于该允许值，因此，a的取值范围可取为(0,1]。

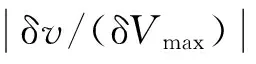
类似地，可以对其他权值项进行设置。至此，线性二次型最优调节问题模型已经建立，根据庞特里亚金极小值原理可对其进行求解。最优控制反馈为：

δu=-R-1BTPδx=-Kδx

(19)

其中，K为最优反馈增益矩阵，P为式(20)Riccati代数方程的解。

PA+ATP+Q-PBR-1BTP=0

(20)

获得最优反馈之后，结合参考轨迹的参考控制量uref，二者累加得实际飞行过程中施加的控制量。

u=uref+δu

(21)

3 仿真计算及结果分析

3.1 仿真条件设置

以高超声速滑翔飞行器CAV-H为仿真对象，其气动参考面积为0.483 9 m2，质量为907 kg，设置最大攻角为15°，最大倾侧角为60°，初始条件设置见表1。

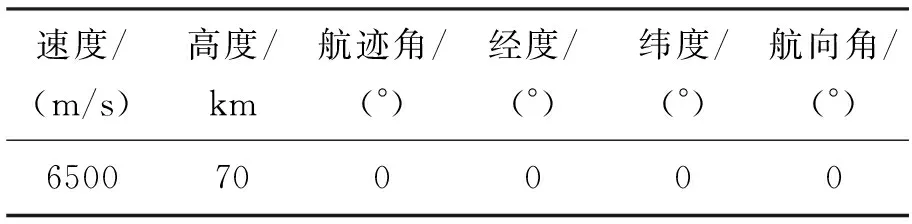
表1 仿真初始条件

终端条件设置为满足起滑要求，即速度倾角为零且速度倾角变化率大于零。进一步，变轨段环境因素复杂，且飞行器自身状态偏差较大，主要考虑的偏差条件包括初始高度偏差、初始速度偏差、初始速度倾角偏差和大气密度、气动参数偏差。

制导参数设置为：a=1,r=1，δhmax=2 km,δVmax=10 m/s,δθmax=0.2°，δαmax=5°,δσmax=15°。

3.2 结果及分析

3.2.1 单项拉偏

在单项拉偏的仿真条件下对变轨段自适应跟踪制导方法正确性进行验证，如图4所示。其中，实线表示标准状态下飞行弹道，其他6条弹道分别表示初始高度拉偏0.6 km，初始速度拉偏30 m/s，初始速度倾角拉偏0.1°，升力系数拉偏30%，阻力系数拉偏30%，大气密度拉偏30%情况下的变轨段实际弹道。

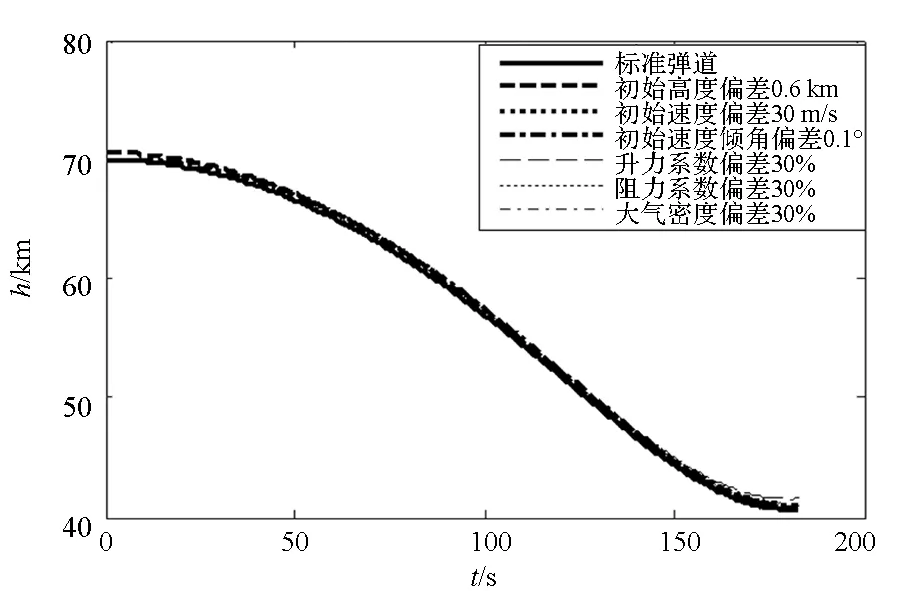
图4 偏差条件下变轨段弹道Fig.4 Trajectory of injection phase under variations

改进自适应跟踪制导方法是将偏差量以一定形式反馈到攻角、倾侧角控制量上，最终完成对偏差条件的修正。对攻角和倾侧角变化曲线进行记录，如图5和图6所示。

图5 攻角变化曲线Fig.5 Changes of attack angle

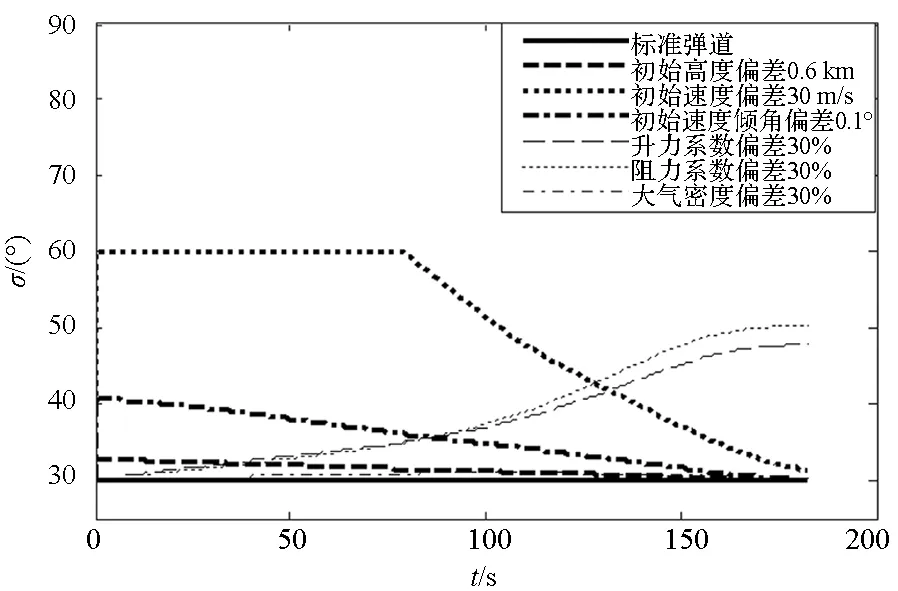
图6 倾侧角变化曲线Fig.6 Changes of bank angle

从不同偏差条件下变轨段弹道仿真来看，该改进自适应跟踪制导方法能够实现对初始偏差以及过程偏差的修正。进一步，整个飞行过程中对速度倾角偏差、速度偏差和气动偏差较为敏感，为主要考虑的偏差因素。

3.2.2 自适应制导优势分析

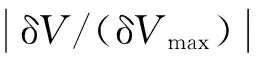
图7 速度误差对比分析Fig.7 Comparation of velocity error

图8 速度倾角误差对比分析Fig.8 Comparation of flight path angle error

仿真结果表明，基于权值矩阵自适应修正的变轨段跟踪制导方法，可以根据当前状态偏差，自适应调整不同状态量之间的权值关系，对偏差较大的状态量进行补偿修正，对偏差较小的状态量进行适当放宽，其实质为一种飞行器制导修正能力的在线自适应调整方法。

3.2.3 蒙特卡洛打靶

偏差条件设置和3.2.1节相同，进行200次蒙特卡洛打靶试验，仿真结果如图9所示。

图9 蒙特卡洛打靶结果Fig.9 Monte Carlo results

从仿真结果可以看出，由于变轨段气动调整能力有限，该改进自适应跟踪制导方法对正向偏差修正能力强，而对负向偏差修正能力较弱。因此，在变轨段跟踪制导方案研究中应考虑变轨段飞行能力，合理设计标准轨迹并给制导系统预留足够的攻角倾侧角控制余量。

4 结论

高超声速滑翔飞行器变轨段调整能力有限，对标准轨迹的跟踪制导必须依据合理的准则对有限能力进行分配。

本文提出的以误差作为反馈量对加权矩阵进行修正的自适应跟踪制导方法，能够根据实际偏差情况，自适应调整高度、速度、速度倾角这三个状态量的加权值，当飞行过程中某一项状态偏差较大时，相应的权值增加，有意地对该项偏差进行纠正，实现对标准轨迹的自适应跟踪。该方法相比于传统的Bryson选取原则来说，具有更好的偏差修正效果。

后续可进一步对状态误差项的反馈形式进行探讨，采用比例、微分甚至指数形式的权值矩阵参数，获得制导指令更加平滑且具备设计者自身偏好的自适应最优跟踪制导方法。

References)

[1] 周浩, 周韬, 陈万春, 等. 高超声速滑翔飞行器引入段弹道优化[J]. 宇航学报, 2006, 27(5): 970-973.

ZHOU Hao, ZHOU Tao, CHEN Wanchun, et al. Trajectory optimization in injection phase for hypersonic gliding vehicle[J]. Journal of Astronautics, 2006, 27(5): 970-973. (in Chinese)

[2] Wang J B, Qu X, Ren Z. Hybrid reentry guidance based on the online trajectory planning[J]. Journal of Astronautics, 2012, 33(9): 1217-1224.

[3] Mooij E. Adaptive heat-flux tracking for re-entry guidance[C]//Proceedings of AIAA/AAS Astrodynamics Specialist Conference, 2014.

[4] Lu P. Entry guidance: a unified method[J]. Journal of Guidance Control & Dynamics, 2014, 37(3): 713-728.

[5] 张蕊, 张冉, 李惠峰. 升力式再入轨迹生成的近似闭环解析方法[C]//第32届中国控制会议， 2013： 5065-5070.ZHANG Rui, ZHANG Ran, LI Huifeng. An approximate analysical method for lifting reentry trajectory generation[C]//Proceedings of the 32nd Chinese Control Conference， 2013： 5065-5070. (in Chinese)

[6] Lu P. Entry guidance and trajectory control for reusable launch vehicle[J]. Journal of Guidance Control & Dynamics, 1997, 20(1): 143-149.

[7] Li D W, Yang B. Reentry guidance for reusable launching vehicle[J]. Journal of Solid Rocket Technology, 2010, 33(2): 119-124.

[8] Vinh N X. Optimal trajectories in atmospheric flight[J]. Space Mankinds Fourth Environment, 1982: 449-468.

[9] 郑总准, 王永骥, 谢富强, 等. 基于H∞鲁棒动态逆的飞行器轨迹跟踪方法[J]. 系统工程与电子技术, 2010, 32(6): 1309-1313.

ZHENG Zongzhun, WANG Yongji, XIE Fuqiang,et al. Trajectory tracking law for hypersonic vehicles based onH∞robust dynamic inversion[J]. Systems Engineering and Electronics, 2010, 32(6): 1309-1313. (in Chinese)

[10] Liang Z X, Ren Z, Shao X Y. Decoupling trajectory tracking for gliding reentry vehicles[J]. Journal of Automatica Sinica, 2015, 2(1): 115-120.

[11] Liu J, Chen K J, Tang G J. Research of equilibrium-glide guidance method based on the generalized reference-trajectory[C]// Proceedings of 6th International Conference in Recent Advances in Space Technologies, Turkey, 2011: 286-290.

[12] Bryson A E, Ho Y C, Siouris G M. Applied optimal control: optimization, estimation, and control[M]. USA:Halsted Press, 1975.

Adaptive tracking guidance method in injection phase forhypersonic glide vehicles

HE Ruizhi1, LIU Luhua1, TANG Guojian1, BAO Weimin1,2

(1. College of Aerospace Science and Engineering, National University of Defense Technology, Changsha 410073, China；2. China Aerospace Science and Technology Corporation, Beijing 100048， China)

According to the trajectory tracking problem of hypersonic glide vehicle under great deviation conditions, a new adaptive tracking guidance method in the injection phase was put forward based on the adaptively revised weighting matrix. The main control mode and standard trajectory characteristics were analyzed. The simplified longitudinal motion equations were linearized near the standard trajectory. An improved adaptive tracking guidance method was designed by introducing the error term in linear quadratic performance index. The simulation results of CAV-H indicate that this method can achieve a great performance in adaptive tracking guidance in the injection phase, and has a good robustness to the initial and process deviation.

hypersonic glide vehicle; injection phase; revised weighting matrix; adaptive tracking guidance

10.11887/j.cn.201605016

http://journal.nudt.edu.cn

2015-05-13

国防科学技术大学科研计划资助项目(ZDYYJCYJ20140101)

何睿智(1990—)，男，江西吉安人，博士研究生，E-mail: heruizhi_nudt@sina.com；汤国建(通信作者)，男，教授，博士，博士生导师，E-mail: tangguojian@nudt.edu.cn

V448

A

1001-2486(2016)05-099-06