超音速子母弹时序抛撒分离干扰特性*
王金龙,王 浩,江 坤,陶如意,王政伟
(南京理工大学 能源与动力工程学院, 江苏 南京 210094)
超音速子母弹时序抛撒分离干扰特性*
王金龙,王 浩,江 坤,陶如意,王政伟
(南京理工大学 能源与动力工程学院, 江苏 南京 210094)
为分析在时序抛撒方式下子母弹多体干扰流场特性及其对各舱段弹体气动特性的影响,基于流体控制方程与六自由度刚体运动方程,结合非结构动网格技术,分别对两种时序抛撒方式及后舱子弹单独抛撒方式下的子母弹三维非定常分离流场进行数值模拟,得到不同抛撒时序下的分离流场特性及其气动干扰特性,揭示各舱段子弹在不同分离阶段的气动干扰相互作用过程。研究结果表明:在时序抛撒分离过程中各弹体间激波不断地交错干扰,增加了流场结构的复杂性;前舱子弹的激波干扰使得后舱段子弹气动分离参数较低,分离效率较慢,尤其在短时序间隔下,后舱弹体受前舱子弹干扰较为严重,弹体的安全分离受到影响。
流体力学;时序抛撒;多体分离;气动特性;数值模拟
子母弹武器系统通过均匀散布大量子弹药,实现大面积毁伤,来弥补射击误差的不足。为了获得较好的散布效果,目前子母弹抛撒系统通常采用时序控制,即各舱段子弹依据抛撒时序依次分离。在子母弹时序抛撒过程中,不仅存在母弹开舱抛撒后由于外形变化引起的气动特性的改变,而且还涉及母弹与子弹、子弹与子弹间的气动干扰,尤其在超音速飞行中,多体之间的激波干扰,使得流场结构异常复杂,增加了系统运动规律的复杂性。因此,对子母弹时序抛撒过程进行研究,分析其抛撒过程中流场结构及气动干扰特性是解决子母弹时序抛撒问题的关键。
目前国内外学者对子母弹多体分离相关问题已进行了大量的研究[1-3],并开展了一系列相关风洞试验研究工作[4-5]。赵忠良[6]、张来平[7]、雷娟棉[8]、张玉东[9]等多位学者对子母弹多体分离过程进行了较为系统的研究,并分析了子母弹分离过程干扰流场特性及气动特性。从目前国内外公开发行文献来看,对于子母弹分离问题的研究多集中于受激波干扰较为严重的前舱子弹,但是对于子母弹多舱段、时序抛撒非定常气动干扰特性及运动特性相关研究较少,而子母弹开舱抛撒过程包含着复杂的动力学过程,子弹药抛撒舱段、抛撒时序间隔对不同舱段弹体间有效分离距离的建立及后续飞行具有重要影响。
因此在前人研究基础上,为考察不同抛撒时序间隔对子母弹分离运动特性的影响,获得子母弹在多舱段、时序抛撒方式下前、后舱段子弹药气动干扰特性规律,本文基于任意拉格朗日欧拉(Arbitrary Lagrange-Euler, ALE)描述下的三维非定常可压缩N-S方程,结合非结构动网格技术,通过耦合求解流体控制方程及六自由度(6 Degree Of Freedom, 6DOF)刚体运动方程,对子母弹在多舱段、时序抛撒方案下分离动力学过程进行了数值模拟,并通过自定义程序对弹体间抛撒时序间隔及前后舱段弹体运动进行控制,对两种时序抛撒方案及后舱子弹药单独抛撒方案下子母弹抛撒分离流场特性及气动干扰特性进行了对比分析。通过多体间的耦合计算,研究结果可为解决子母弹在多舱段、时序抛撒下相关问题提供新的参考。
1 数值计算方法
1.1 控制方程及湍流模型
ALE有限体积法描述下的三维非定常可压缩N-S方程其积分形式表达式为:

(1)
式中,Ω为控制体体积,S为控制体表面边界,n为控制体边界外法向单位向量,守恒变量Q及对流项为:
(2)
控制方程右端为作用在控制体表面的黏性通量:
H(Q)=E·i+F·j+G·k
(3)
其中:ρ,p,e分别为控制体内流体密度、压强及比内能;nx,ny,nz分别为外法向单位向量n的三个分量;u,v,w分别为速度在三个方向上的分量;τij为不同方向上Reynolds应力项;
U={(u-xt),(v-yt),(w-zt)}
uw=xtnx+ytny+ztnz
Π1=uτxx+vτxy+wτxz+qx
Π2=uτyx+vτyy+wτyz+qy
Π3=uτzx+vτzy+wτzz+qz
其中,xt,yt,zt分别为网格移动速度在三个方向的分量,qx,qy,qz为微元热流量。为使方程组封闭,补充能量方程:
(4)
式中,γ为空气比热比。对于上述控制方程基于有限体积法进行空间离散,时间项采用隐式向后差分格式,对流项采用具有较高精度被广泛采用的迎风格式中二阶隐式AUSM(advection upstream splitting method)格式,对于湍流的计算则采用Realizablek-ε双方程湍流模型,此模型对于不同雷诺数下边界层流动和分离的流动等均有较好的适应性,湍流黏性系数由湍动能k和湍流耗散率ε求得。
1.2 耦合求解方法
为实现子母弹分离过程流场区域的更新,通过编译了6DOF气动耦合程序,将刚体动力学方程耦合流体控制方程求解,网格更新过程根据每个迭代步中边界的变化情况自动完成。6DOF刚体动力学方程组详见文献[10],耦合求解过程如图1所示,具体过程如下:

图1 耦合求解流程图Fig.1 Flow chat of coupling resolution
1)为保证非定常计算的准确性,首先对子母弹初始流场进行定常求解,得到其流场气动载荷分布,将其作为非定常流场计算的初始流场,并沿弹体表面对压力进行积分求得子弹所受气动力;
2)以子弹当前气动载荷以及子弹初始运动参数作为流场计算的初始条件,调用6DOF动力学方程求解,获得下一时刻子弹位置、速度及姿态角等;
3)根据新的边界值计算出子弹药相对母弹移动后网格节点位置,运用弹簧光顺法和局部网格重构法对子弹动边界进行网格的更新与重构,并进行下一步迭代计算,从而实现整个流场区域的更新。
2 计算条件
2.1 计算模型
图2为时序抛撒子母弹计算模型,分别选取时序间隔Δt1=10 ms,Δt2=20 ms两种不同的抛撒时序方案,即前舱子弹在后舱子弹抛出10 ms,20 ms后开舱抛撒。为了与试验结果进行比较,采用与风洞试验相同的弹形和状态,其中弹体质量M=28 kg,转动惯量Ixx=0.39 kg·m2,Iyy=Izz=3.435 kg·m2,弹体质心位置与子弹尾部距离L=246.8 mm。因采用囊式抛撒技术,因此认为子弹药距母弹弹舱具有一个气囊膨胀高度距离间隔,其间隔距离为d=110 mm。母弹包含前后两层弹舱,为节约计算时间、提高计算效率,取整个区域的1/4作为计算区域。外流场区域整体采用四面体非结构网格划分,网格数量约为200万。为保证计算过程中子弹动区域周围网格质量,对弹丸周围部分区域加密网格,以提高求解精度。

图2 时序抛撒子母弹计算模型Fig.2 Computational model of sub-munition under sequential separation
2.2 边界条件
边界条件包括固壁边界及流场外边界,其中前后舱段子弹为移动固壁,母弹为静止固壁,物面上法向为无穿透条件,子弹沿x轴方向初始速度为零。来流边界取自由来流边界条件,出流边界采用场内外推处理。流场初始参数:来流马赫数Ma=3,压力为1个标准大气压,温度T为300 K。为保证抛撒的有效性,弹体抛撒速度及抛撒角速度依据课题组试验结果及数值计算结果选取,子弹初始抛速v=16 m/s,角速度ω=500°/s,抛撒时序间隔分别为Δt1=10 ms,Δt2=20 ms。
3 计算结果及分析
为验证文中数值计算方法在捕捉流场结构特征上的准确性,选取某时刻时序抛撒计算结果与风洞试验纹影图进行对比分析,试验弹体模型状态包括质心位置、姿态等,由计算结果获得,对比结果如图3所示。

图3 试验纹影图与计算结果对比图Fig.3 Contrast between experiment and simulation results
由图3可以看出,母弹激波作用于前舱子弹头部,在子弹头部产生高压区并形成斜激波,部分弹体激波随母弹主流激波向后发展,同时部分激波向下发展作用于母弹弹舱表面形成反射波,由于母弹弹肩后台阶膨胀波及弹槽空腔的作用,在子弹下表面形成一个三角形低压区域。随着子弹位移及攻角的增加,母弹激波、前舱子弹激波作用于后舱子弹头部下表面,使得弹体头部压力逐渐增加。通过与试验结果的对比,可以看出文中所采用的数值方法能够较好捕捉子母弹时序抛撒流场细节特征,计算结果与试验结果吻合良好。
3.1 时序1状态抛撒计算结果分析
为检验时序抛撒间隔对子母弹分离品质的影响,分别对子母弹在时序间隔Δt1=10 ms,Δt2=20 ms状态下的分离过程进行数值模拟。
图4为时序1即前后舱子弹间隔Δt1=10 ms抛撒状态下子母弹分离过程x-y剖面压力分布云图。由图可以看出,初始阶段后舱子弹处于前舱子弹尾激波影响下;10 ms后后舱子弹头部逐渐进入母弹激波和子弹激波,此时前舱子弹开始抛出并进入母弹激波;21 ms后前舱子弹头部摆脱母弹激波影响,母弹激波作用于前舱子弹下表面,在来流及母弹激波的共同影响下,前舱子弹分离效率加快,而后舱段子弹未能及时摆脱激波影响,长期处于前舱子弹激波及母弹激波干扰下。
图5、图6分别为10 ms后前、后舱段子弹药升、阻力系数随时间变化曲线,由计算结果可以看出前舱子弹在抛出后受母弹激波影响其升、阻力系数增幅较大,而后舱段子弹由于受到前舱子弹的干扰,其气动参数相对较弱,导致前后舱段弹体不断逼近,弹体间未能建立有效的分离距离,分离效果不理想。

图4 时序1状态抛撒过程压力分布云图Fig.4 Pressure contours of sequential separation 1

图5 前后舱段子弹升力系数变化曲线Fig.5 Lift characteristic of the bullets

图6 前后舱段子弹阻力系数变化曲线Fig.6 Drag characteristic of the bullets
3.2 时序2状态抛撒计算结果分析
图7为时序2即Δt2=20 ms抛撒状态下子母弹分离过程压力分布云图。前舱子弹在后舱子弹抛出20 ms后开始抛撒,分离初期后舱子弹弹体所受气动干扰较弱,随着子弹位移的增加,在20 ms时子弹头部完全进入母弹激波及前舱子弹激波下,在弹体头部形成高压区。此时,前舱子弹开始运动并逐步进入母弹激波,30 ms后前舱子弹头部脱离母弹激波,母弹激波作用于前舱子弹下表面。随着分离时间的增加,母弹激波逐步扫过前舱弹体表面,母弹激波作用点向弹体尾部移动,此时母弹激波、前舱子弹激波、后舱子弹激波、弹舱反射波等多个波系间形成复杂的相交干扰。在整个时序抛撒分离过程中,后舱子弹长期受到母弹激波和前舱子弹激波的影响,母弹激波、前舱子弹激波的干扰不仅为弹体的分离提供了轴向力及法向力,而且为子弹的俯仰运动提供了力矩,使得整个分离过程中后舱子弹攻角不断增加。
3.3 子弹单独抛撒计算结果分析
为分析在时序抛撒状态下前舱子弹对后舱子弹气动干扰特性的影响,对后舱子弹单独抛撒状态进行了数值模拟。图8为后舱子弹抛出20 ms后分离过程压力分布云图,后舱子弹抛撒前0~20 ms分离状态与图8中所示一致。结合图4、图7、图8可以看出,在时序抛撒状态下前舱子弹受后舱子弹影响甚微,其分离流场结构并未发生较大改变。来流对后舱子弹的影响是明显存在的,但由于前舱子弹及母弹激波的影响,后舱子弹分离效率降低。尤其在抛撒时序间隔较小时,前舱子弹对后舱子弹干扰较为严重,影响弹体的安全分离。


图7 时序2状态抛撒过程压力分布云图Fig.7 Pressure contours of sequential separation 2

图8 后舱子弹单独抛撒过程压力分布云图Fig.8 Pressure contours of independent separation
3.4 气动参数分析
在时序1状态下,后舱子弹在10 ms内未能建立较大的分离距离,前舱子弹抛出后所受升、阻力较后舱子弹大,使得前后舱段弹体间距离不断减小,分离效果不理想。为分析时序抛撒方式下前舱子弹对后舱子弹气动参数的影响,现分别对后舱子弹在单独抛撒及时序2状态下的分离气动参数进行分析,其计算结果如图9~12所示。
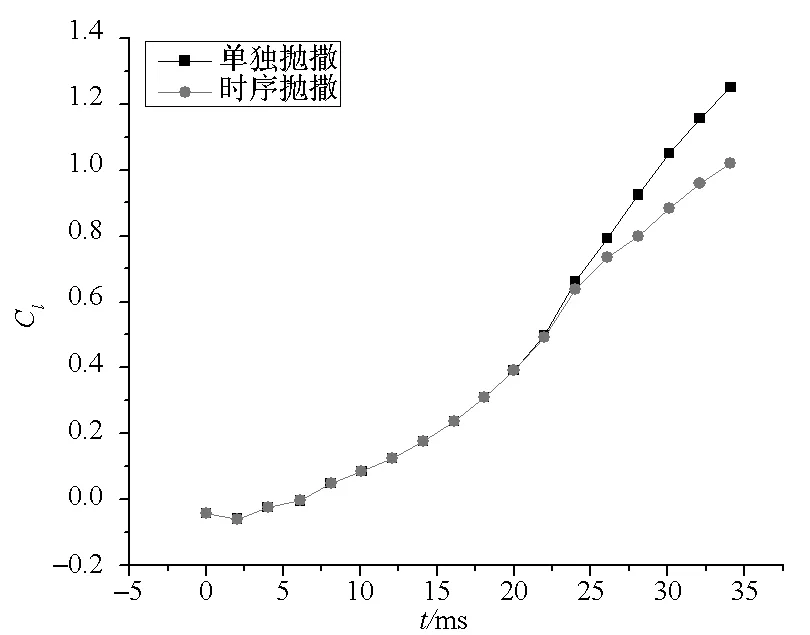
图9 升力系数随时间变化曲线Fig.9 Lift characteristic of bullet 2 along time

图10 阻力系数随时间变化曲线Fig.10 Drag characteristic of bullet 2 along time
图9、图10分别为时序2状态抛撒和子弹单独抛撒方式下,后舱子弹升、阻力系数随时间变化曲线。结合图7可以看出,在分离前期0~20 ms内后舱子弹在自身抛速及角速度影响下,弹体位移及攻角不断增加,在来流及母弹激波的干扰下,其升、阻力系数不断增加。20 ms后随着前舱子弹的抛出,由于后舱子弹长期处于前舱子弹激波下,弹体未能及时摆脱激波干扰影响,其升、阻力系数增长较缓。而在子弹单独抛撒状态下,由于后舱子弹在20 ms后弹体头部逐渐摆脱激波影响,在母弹激波、前舱子弹激波及来流的共同作用下,其升、阻力系数相比时序抛撒时高。

图11 子弹沿y方向相对速度变化曲线Fig.11 Relative velocity of bullet 2 along y direction

图12 后舱子弹角速度随时间变化曲线Fig.12 Pitching angle velocity of bullet 2 along time
在时序1方案下,20 ms后前、后舱段弹体间距离不断缩短,将引发弹体间发生碰撞,导致计算过程停止。为分析时序间隔对弹体运动特性影响,现分别对时序1、时序2及单独抛撒下弹体相对分离速度及分离角速度变化过程进行分析。
图11分别为时序1、时序2及单独抛撒状态下后舱子弹径向相对速度随时间变化曲线。在分离初始阶段由于弹体表面气动力较弱及克服自身重力影响的关系,子弹分离速度逐渐减小。随着后舱子弹位移及攻角的增加,母弹激波及前舱子弹激波对后舱子弹干扰力的逐渐增强为后舱子弹的分离提供了法向力,使得子弹分离速度逐渐增加。通过相对速度曲线对比可知,在时序抛撒方式下由于前舱子弹的干扰作用,后舱弹体分离速度相比单独抛撒状态下较低,但效果并不明显。而在时序1抛撒方案下,由于后舱子弹在前舱子弹的干扰下未能及时分离,其分离速度相比时序2状态较低。
图12为时序1、时序2及单独抛撒状态下角速度变化曲线。分离初期子弹克服激波运动,使得弹体产生沿z轴正方向的俯仰力矩,但在其自身初始角速度的影响下,子弹分离攻角逐渐形成,此时母弹激波及子弹激波主要作用于弹体头部下表面,为子弹提供了沿z轴负方向的俯仰力矩,使得子弹攻角逐渐增加。通过角速度曲线对比可以看出,在时序抛撒方式下20 ms后后舱子弹角速度下降幅度较子弹单独抛撒时慢。这是由于在单独抛撒状态下,20 ms后后舱子弹头部逐步摆脱激波,来流的作用为后舱弹体提供了额外的俯仰力矩,从而其角速度下降较快。由于前舱子弹的持续干扰,后舱子弹未能及时摆脱激波影响,时序1状态下弹体分离角速度比时序2状态下变化过程较为缓慢。
4 结论
以双层弹舱轴向排布时序抛撒子母弹系统为模型,通过自定义耦合求解程序实现对抛撒时序间隔及弹体边界的运动的控制,分别对子母弹时序抛撒多体分离过程进行了数值模拟,数值模拟结果与试验结果的对比验证了本文所采用数值方法对于子母弹在多舱段、时序抛撒方案下的非定常多体分离过程计算的有效性,并得到如下结论:
1)在时序抛撒方式下,母弹激波、前舱子弹激波、后舱子弹激波及母弹弹舱反射波等多个波系间不断地相交干扰,增加了系统运动规律的复杂性。
2)在整个时序抛撒分离过程中,前舱子弹受后舱子弹干扰影响较弱,而后舱子弹由于长期受到前舱子弹激波干扰,分离较为缓慢,整体气动参数较单独抛撒时较低。
3)当抛撒时序间隔较短(10 ms)时,后舱段子弹受前舱子弹干扰较为严重,弹体间未能建立有效分离距离,而在时序间隔20 ms状态下,后舱弹体虽然仍受到前舱弹体激波的干扰影响,但整体上已不影响其分离运动。 因此在本文计算工况下,为保证弹体间的安全分离,其抛撒时序间隔不应低于20 ms。
References)
[1] Demir H O, Alemdraroglu N.Trajectory calculation of a store released from a fighter aircraft[C]//Proceedings of 43rd AIAA Aerospace Sciences Meeting and Exhibit, 2005.
[2] Rizk M, Jolly B. Aerodynamic simulation of bodies with moving components using CFD overset grid methods[C]//Proceedings of 44th AIAA Aerospace Sciences Meeting and Exhibit, 2006.
[3] Panneerselvam S, Nagarajan V, Soundararajan P. Dispenser induced aerodynamic interference loads on submunition during dispense[C]//Proceedings of 15th Applied Aerodynamics Conference, 1997.
[4] Snyder D O, Koutsavdis E K, Anttonen J S R. Transonic store separation using unstructured CFD with dynamic meshing[C]//Proceedings of 33rd AIAA Fluid Dynamics Conference and Exhibit, 2003.
[5] Panagiotopoulos E E, Kyparissis S D. CFD transonic store separation trajectory predictions with comparison to wind tunnel investigations[J]. International Journal of Engineering, 2010, 3(6): 538-553.
[6] 赵忠良, 龙尧松, 余立, 等.高超声速风洞子母弹分离干扰测力试验技术[J].流体力学实验与测量, 2004, 21(3): 32-35.
ZHAO Zhongliang, LONG Yaosong, YU Li,et al. Hypersonic wind tunnel interference force test of submunition reentry separation[J]. Experiments and Measurements in Fluid Mechanics, 2004, 21(3): 32-35.(in Chinese)
[7] 张来平, 杨永健, 张涵信.子母弹分离数值模拟[C]//第十二届全国计算流体力学会议论文, 2004: 47-52.
ZHANG Laiping, YANG Yongjian, ZHANG Hanxin. The numerical simulation of cluster munition[C]//Proceedings of the 12th Computational Fluid Dynamics Conference, 2004: 47-52.(in Chinese)
[8] 雷娟棉, 苗瑞生, 居贤铭. 战术火箭子母战斗部第一次抛撒分离多体干扰流场数值模拟[J]. 北京理工大学学报, 2004, 24(9): 766-769.LEI Juanmian, MIAO Ruisheng, JU Xianming.Numerical simulation of multi-body interference aerodynamic performance of cluster munition dispensed by sequential[J]. Journal of Beijing Institute of Technology, 2004, 24(9): 766-769. (in Chinese)
[9] 张玉东, 纪楚群. 多体分离非定常气动特性数值模拟[J].空气动力学学报, 2006, 24(1): 1-4.
ZHANG Yudong, JI Chuqun. The numerical simulation of unsteady multi-body separation flows[J]. Acta Aerodynamica Sinica, 2006, 24(1): 1-4. (in Chinese)
[10] 韩子鹏. 弹箭外弹道学[M]. 北京:北京理工大学出版社, 2008.
HAN Zipeng. Exterior ballistics of the rockets [M]. Beijing:Beijing Institude of Press, 2008. (in Chinese)
Aerodynamic interference investigation of supersonic cluster munition dispensed by sequence
WANG Jinlong, WANG Hao, JIANG Kun, TAO Ruyi, WANG Zhengwei
(School of Energy and Power Engineering, Nanjing University of Science & Technology, Nanjing 210094, China)
In order to analyze the multi-body flow characteristics and the aerodynamic interference characteristics for the sub-munitions in different bays under sequential separation, the three-dimensional unsteady flow field of the cluster munition under two types of sequential separation and single separation style was simulated with the use of the unstructured dynamic mesh method, based on the governing equations of fluid dynamics and rigid body motion equations of 6DOF (degree of freedom). The variation of the flow characteristics and the aerodynamic interference characteristics of sub-munitions in different separation styles was shown and the interaction process of aerodynamic interference between the sub-munitions in different separation stages was revealed as the results. Numerical simulation results show that the flow characteristics become more complicated and the aerodynamic separation parameters of the rear sub-munition become lower than that of the front sub-munition because of the shock wave interaction between the sub-munitions in the process of sequential separation. During the short sequential separation, the interference from the front sub-munition to the rear sub-munition is more severe so that the security of the separation between the sub-munitions is affected.
fluid mechanics; sequential separation; multi-body separation; aerodynamic characteristics; numerical simulation
10.11887/j.cn.201605017
http://journal.nudt.edu.cn
2015-05-04
江苏省高校科研创新计划资助项目(AE91316)
王金龙(1989—),男,江苏盐城人,博士研究生,E-mail: wxj891231@163.com; 王浩(通信作者),男,教授,博士,博士生导师,E-mail:wanghao@mail.njust.edu.cn
V211.3
A
1001-2486(2016)05-105-07

