带有模糊干扰观测器的高超声速飞行器一体化制导控制方法*

赵 暾，王 鹏，刘鲁华，吴 杰

(国防科技大学 航天科学与工程学院， 湖南 长沙 410073)



带有模糊干扰观测器的高超声速飞行器一体化制导控制方法*

赵 暾，王 鹏，刘鲁华，吴 杰

(国防科技大学 航天科学与工程学院， 湖南 长沙 410073)

为充分利用高超声速飞行器在俯冲段的质心运动与绕质心运动之间的耦合作用和飞行过程中的不确定性，基于模糊干扰观测器提出三维一体化制导与控制问题。根据飞行器的动力学方程以及飞行器-目标的视线角相对运动方程，推导出适用于倾斜转弯控制的一体化制导控制模型。针对模型中的不确定性采用模糊干扰观测器进行补偿，并使用块动态面方法设计一种一体化制导控制律。通过选取适当的李雅普诺夫函数证明闭环系统状态的一致毕竟有界性。仿真结果验证了该一体化制导控制方法的有效性和鲁棒性。

高超声速飞行器；模糊干扰观测器；一体化制导控制；块动态面反演控制

高超声速飞行器在俯冲段的状态会发生剧烈变化[1-2]，导致质心运动确定的制导系统和姿态运动确定的控制系统的时间常数会比较接近。传统的基于时标分离原则按照时间常数大小将制导和控制系统分开设计的方法将不适用于俯冲运动的高超声速飞行器。因此需要将制导系统和控制系统作为一个整体进行考虑。高超声速飞行器一体化制导控制设计，是指将飞行器的制导系统和控制系统作为一个整体来进行设计，通过飞行器与目标的相对运动信息直接产生舵偏指令。在设计过程中，由于一体化设计充分开发利用了制导系统与控制系统之间的相互耦合影响，所以可以提升制导控制系统的整体性能。而且传统的制导和控制系统独自分别设计各自系统，然后将两个系统连接起来，再验证整个系统是否满足性能指标。若不满足，则需要对制导系统和控制系统进行迭代设计，这会花费很大的成本。然而，用一体化方法设计的控制律可以从理论上实现整个闭环系统的稳定性，并且不需要进行迭代。这样会降低制导控制系统的设计成本。

一体化制导控制设计方法在1983年由Williams[3]等提出。经过20多年的发展，现有一体化方法采用的模型主要分为三维的相对位置模型和既有平面又有三维的视线角模型[4]。针对这些模型，有许多方法被用来设计一体化制导控制律。Menon[5-6]，Vaddi[7]和Xin[8]等分别采用状态相关Riccati方程方法和θ-D方法针对相对位置模型和视线角模型设计了一体化制导控制律。这两种方法的明显缺点是需要在线求解Riccati方程。Yuri[9]，Shima[10]和Idan[11]等使用滑模控制方法对追踪器与拦截器设计了一体化制导控制律。而Hou等[12]对寻的导弹攻击固定目标在俯仰平面内采用滑模控制方法设计了一体化制导控制律。Tournes等[13]采用子空间稳定方法对末制导和自动驾驶仪进行了一体化设计。Hou等[14]针对寻的导弹攻击固定目标和移动目标，基于自适应块动态面控制方法分别设计了俯仰平面内全量耦合的一体化制导控制律。Guo等[15]考虑了飞行器纵向平面内模型，采用鲁棒控制方法设计了一体化制导控制律。

已有文献大多都针对寻的导弹的末制导段进行一体化制导控制，这种类型的控制策略都是采用侧滑转弯技术。而本文研究的高超声速飞行器在俯冲段采用的是倾斜转弯控制，所以已有文献的控制构型并不适用本文的研究对象。目前文献所设计的一体化制导控制律中，大多都将飞行器状态方程中的干扰作为有界的不确定项来处理。而在实际设计中，干扰的上界是很难估计的。因此，本文采用模糊干扰观测器(Fuzzy Disturbance Observer，FDO)来逼近未知的不确定项，从而使得所提出的一体化制导控制方法具有较强的鲁棒性。

1 飞行器数学模型

在建立面向控制的飞行器状态方程时，基于下面的假设条件：

1)只考虑飞行器本体产生的气动力，而将舵偏角的影响作为不确定项；

2)高超声速飞行器在俯冲段的侧向力几乎为零；

3)地球为一不旋转的均质圆球。

1.1 飞行器气动模型

在建立面向控制的模型中，对气动力和气动力矩的拟合公式进行简化。在处理过程中把次要因素作为不确定项，则气动力和气动力矩在面向控制的模型中可以表示为：

(1)

1.2 绕质心运动方程

飞行器绕质心运动模型可以由式(2)表示。

(2)

其中：Δx′1和Δx2为不确定未知有界函数向量，Δx′1包含了侧向力N的影响，Δx2包含了ΔMx，ΔMy和ΔMz等不确定未知有界标量函数。

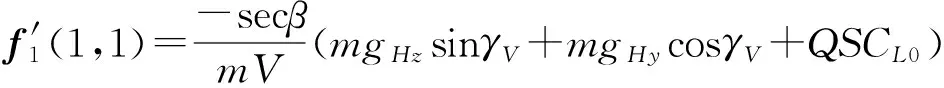
(tanθ+tanβsinγV)mgHz+

(tanθsinγV+tanβ)QSCL0]

其中：m为飞行器的质量；α为攻角；β为侧滑角；γV为倾侧角；Ii(i=x,y,z)分别为飞行器相对体坐标系三轴的转动惯量；θ为速度倾角；gHx，gHy和gHz为重力加速度在半速度系中的分量。

1.3 飞行器与目标相对运动方程

如图1所示，以目标北天东坐标系为参考系计算飞行器的视线角。视线坐标系的原点固定在目标点，osx轴由目标点指向飞行器质心，osz轴在目标点水平面内，osy轴与osx轴和osz轴构成右手坐标系。λD和λT分别为视线倾角和视线偏角。

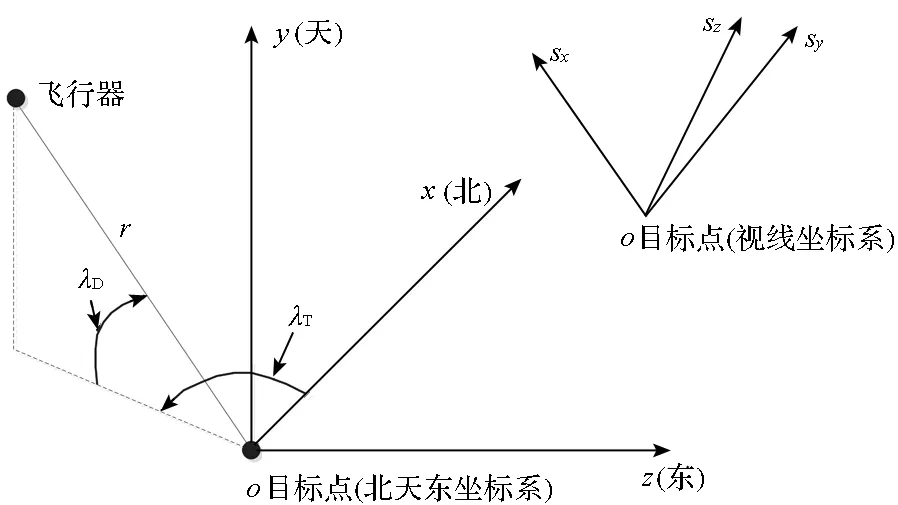
图1 北天东坐标系和视线坐标系示意图Fig.1 Diagram of NRE coordinate system and LOS coordinate system

飞行器和目标的相对运动可以表示为：

(3)

其中：r为飞行器相对于目标点的距离；ar，aλD和aλT分别为飞行器相对于地面的加速度矢量在视线坐标系三个轴向的分量。

在制导律设计中，一般选择视线角速率为控制量，当其被控制到零时，即可认为飞行器最终可到达目标点。因此，可以只考虑视线角运动方程。

(4)

2 一体化制导控制律设计

2.1 面向控制的一体化制导控制模型

飞行器加速度矢量在视线坐标系sy轴和sz轴的分量为：

(5)

其中：SHi,j(i,j=1,2,3)分别为半速度系到视线系的转换矩阵SH中的元素，i表示行，j表示列；aV，aθ和aσ分别为飞行器加速度在半速度系三个轴向的分量，可表示为：

(6)

其中：Δθ和Δσ为侧向力引起的不确定未知有界标量函数。

考虑气动力的主要影响因素，并将次要因素作为不确定未知有界标量函数，则有：

(7)

(8)

其中：ΔV为包含Δ′D的不确定未知有界标量函数；Δ′θ为包含Δθ和Δ′L的不确定未知有界标量函数；Δ′σ为包含Δσ和Δ′L的不确定未知有界标量函数。

现在，令

(9)

则由式(4)、式(5)和式(8)可以得到面向控制的视线角运动方程为：

(10)

其中： f0(x0)中各元素可以表示为

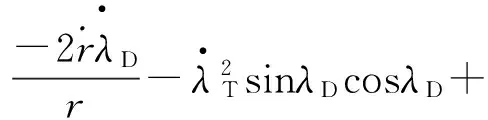
Δx0为包含ΔV，Δ′θ和Δ′σ的不确定未知有界函数向量。

从式(9)中选取的状态变量可以看出，为建立一体化制导控制方程，需要对绕质心运动方程进行变换。现在，选取绕质心运动状态变量为：

(11)

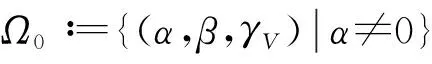
(12)

其中：

g1(x1)中各元素可以表示为

g1(1,1)=-cosα(tanβcosγV+αsecβsinγV)，

g1(1,2)=sinα(tanβcosγV+αsecβsinγV)，

g1(1,3)=cosγV，

g1(2,1)=cosα(αsecβcosγV-tanβsinγV)，

g1(2,2)=-sinα(αsecβcosγV-tanβsinγV)，

g1(2,3)=sinγV, g1(3,1)=sinα，

g1(3,2)=cosα, g1(3,3)=0。

综上所述，联立式(10)、式(12)和式(2)中的第二式得到一体化制导控制模型

(13)

其中：Δx0，Δx1和Δx2为不确定未知有界函数向量，Δx0和Δx1为非匹配不确定因素，Δx2为匹配不确定因素。

对于g1(x1)可得：

det[g1(x1)]=αsecβ

(14)

(15)

内取值时，可知g1(x1)是可逆的。且Ω1为2中的有界闭集，即Ω1为一个紧集。

对于g2(t)可得：

(16)

由飞行器的气动数据可知，g2(t)在俯冲段是非奇异的，即g2(t)是可逆的。

根据集合Ω0和Ω1，做出如下假设。

假设1：飞行器在整个受控飞行过程中，(α,β)总在集合Ω1中取值。

可以看出，式(13)满足块严格反馈形式，因此可以基于块反演方法来设计系统的控制器。式(13)中的不确定项可以用模糊干扰观测器进行补偿。

2.2 模糊干扰观测器设计

在控制器设计中，用模糊干扰观测器来估计不确定项Δx0，Δx1和Δx2。

一个模糊逻辑系统基本由以下四部分组成：模糊器、模糊规则、模糊推理机和反模糊器。根据模糊系统的万能逼近定理，由单值模糊器、高斯隶属度函数、乘积推理器和中心平均解模糊器构成的模糊系统可以以任意精度一致地逼近定义在紧集U上的任意非线性函数[17]。

现在设计可以逼近Δx0的模糊系统，对于其余两个不确定项可以采用类似方法。

(17)

(18)

定义最优逼近参数为：

(19)

则，最小逼近误差为：

(20)

令s0=x0，设计θj满足自适应律。

θj=γs0jζ(x0)

(21)

2.3 一体化制导控制方法

为简化起见，将fi(·)和gi(·)分别记为fi和gi。

基于自适应块动态面设计控制器公式为：

(22)

2.4 稳定性分析

定义滤波误差为：

(23)

定义逼近误差为：

(24)

定义李雅普诺夫函数为：

(25)

其中：

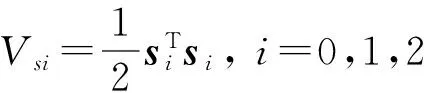
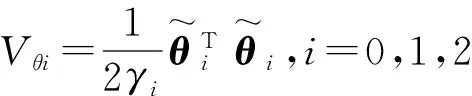
动态面的导数为：

(26)

同样地，滤波误差的导数为：

(27)

对V求导，各项的导数为：

(28)

其中：

(29)

同样地，

(30)

由于k0都为对角阵，则

(31)

滤波误差项可以变换为：

(32)

将式(29)～(32)代入式(28)并求和可以得到：

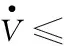
(33)

对于虚拟控制的导数，存在两个非负的连续函数d1和d2，满足

(34)

给定一个正数p，集合

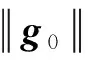
选取参数满足

(35)

自适应律为：

(36)

则式(33)可以变换为：

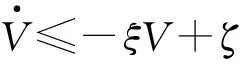
(37)

(38)

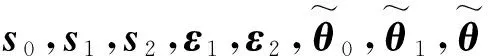
3 仿真分析

假设飞行器的初始状态和目标的位置如表1所示。

表1 飞行器和目标的状态初值

表1中，φ0和λ0为发射点的经、纬度，φT和λT分别为目标点的经、纬度。控制器参数选取为：

k0=diag(5,0.05)，k1=diag(15,15,10)，

k2=diag(30,20,50)，τ1=diag(0.05,0.05)，

τ2=diag(0.05,0.05,0.05)，γ0=γ1=γ2=10。

在仿真过程中，考虑到实际情况，飞行器的舵偏进行如式(30)所示的限定：

(39)

为了验证控制算法(式(22))的鲁棒性能，仿真中考虑了飞行器的气动力系数、气动力矩系数、转动惯量与大气密度相对于标称值减小30%、不变和相对于标称值增大30%的三种情况。仿真结果如图2～7所示。

图2 攻角、侧滑角和倾侧角随时间变化曲线Fig.2 Curves of attack angle, sideslip angle and bank angle

图3 滚转、偏航和俯仰角速率随时间变化曲线Fig.3 Curves of roll rate, yaw rate and pitch rate

图4 舵偏角随时间变化曲线Fig.4 Curves of deflection angle

图5 飞行器的空间曲线Fig.5 3D vehicle trajectory

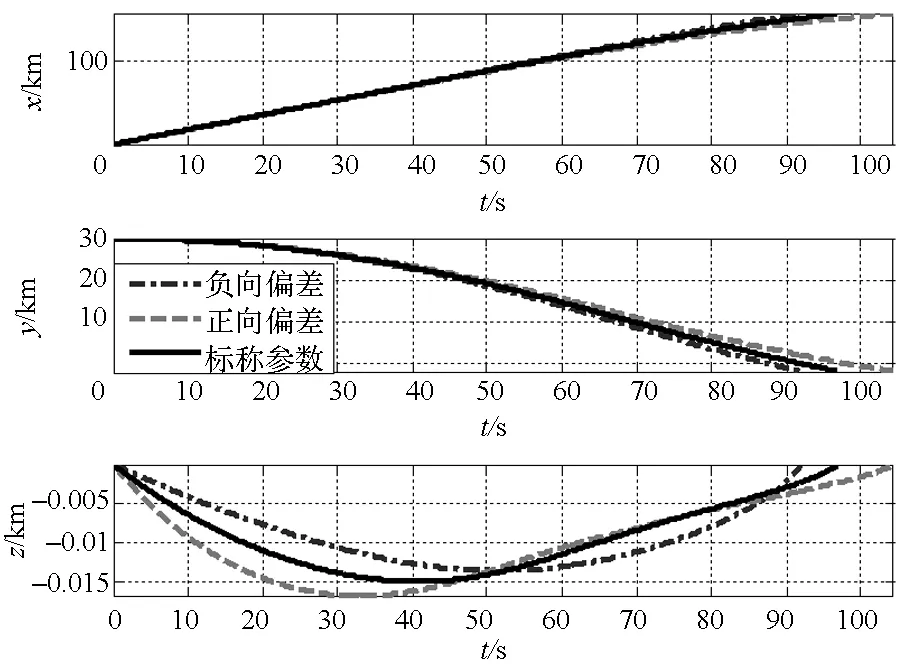
图6 飞行器位置在发射系中分量的变化曲线Fig.6 Curves of vehicle position projecting in launch coordinate system

图7 过载变化曲线Fig.7 Curves of overload

仿真得到在标称参数、正向偏差和负向偏差情况下，飞行器的脱靶量分别为0.58 m，1.91 m和5.44 m。由图2和图3可知，在整个飞行过程中，飞行器的姿态是稳定的，侧滑角的变化幅度很小基本保持在0°左右。而倾侧角和滚转角速度在接近目标点时存在较大的变化，这是由于飞行器在接近目标点时，其距离目标还有一段侧向距离，因此飞行器需要一个较大的倾侧角来让升力的分量产生侧向力以消除侧向距离，为了产生这个较大的倾侧角，对应需要较大的滚转角速度。由图4可知，舵偏角除了在开始俯冲时变化较大外，其余飞行阶段的变化幅度均保持在合理的范围内。由图5和图6可知，飞行器在整个俯冲过程弹道变化平滑。由图7可知，过载保持在合理的范围之内。

对算法的鲁棒性进行考察可知，参数发生摄动情况下和标称情况下相比，飞行器的脱靶量与状态的变化曲线相差很小。但是当参数相对于标称值存在负向偏差时，飞行器具有较大的脱靶量和动压。

4 结论

本文提出的一体化制导控制方法主要有以下两个优点：第一，通过块动态面反演方法可以充分利用高超声速飞行器的质心与绕质心之间的耦合作用，这样可以提高制导精度和控制性能；第二，采用模糊干扰观测器对不确定项进行补偿使得一体化制导控制律有较强的鲁棒性。仿真结果表明，在标称条件和参数偏差的影响下，飞行器采用本文方法均有较小的脱靶量，并且在飞行过程中状态保持稳定。

References)

[1] Wang P, Tang G J, Liu L H, et al. Nonlinear hierarchy-structured predictive control design for a generic hypersonic vehicle[J]. Science China Technological Science, 2013, 56(8): 2025-2036.

[2] 王鹏, 刘鲁花, 吴杰. 临近空间飞行器纵向逆控制系统设计[J]. 国防科技大学学报， 2012, 34(3): 29-37.

WANG Peng, LIU Luhua, WU Jie. Longitudinal inversion control system design for near-space vehicle[J]. Journal of National University of Defense Technology, 2012, 34(3): 29-37. (in Chinese)

[3] Williams D E, Richman J, Friedland B. Design of an integrated strap down guidance and control system for a tactical missile[C]//Proceedings of AIAA Guidance and Control Conference, 1983: 57-66.

[4] 薛文超, 黄朝东, 黄一. 飞行制导控制一体化设计方法综述[J]. 控制理论与应用, 2013, 30(12): 1511-1520.

XUE Wenchao, HUANG Chaodong, HUANG Yi. Design methods for the integrated guidance and control system[J]. Control Theory & Applications, 2013, 30(12): 1511-1520. (in Chinese)

[5] Menon P K, Ohlmeyer E J. Integrated design of agile missile guidance and control system[C]//Proceedings of the 7th Mediterranean Conference on Control and Automation, 1999:1469-1494.

[6] Menon P K, Ohlmeyer E J. Integrated guidance-control systems for fixed-aim warhead missiles[C]//Proceedings of AIAA Missile Sciences Conference, 2000.

[7] Vaddi S S, Menon P K. Numerical SDRE approach for missile integrated guidance-control[C]//Proceedings of AIAA Guidance, Navigation and Control Conference and Exhibit, 2007.

[8] Xin M, Balakrishnan S N, Ohlmeyer E J. Integrated guidance and control of missiles withθ-D method[J]. IEEE Transactions on Control Systems Technology, 2006, 14(6):987-992.

[9] Shtessel Y B, Shkolnikov I A. Integrated guidance and control of advanced interceptors using second order sliding modes[C]//Proceedings of the 42nd IEEE Conference on Decision and Control, 2003.

[10] Shima T, Idan M, Golan O M. Sliding-mode control for integrated missile autopilot guidance[J]. Journal of Guidance, Control and Dynamics, 2006, 29(2): 250-260.

[11] Idan M, Shima T, Golan O M. Integrated sliding mode autopilot-guidance for dual-control missiles[J]. Journal of Guidance, Control and Dynamics, 2007, 30(4):1081-1089.

[12] Hou M Z, Duan G R. Integrated guidance and control for homing missiles against ground fixed targets[J]. Chinese Journal of Aeronautics, 2008, 21(2): 162-168.

[13] Tournes C, Paschal N, Wilkerson P. Integrated terminal guidance and autopilot using subspace-stabilization[C]//Proceedings of AIAA Guidance, Navigation and Control Conference and Exhibit, 2001.

[14] Hou M Z, Liang X L, Duan G R. Adaptive block dynamic surface control for integrated missile guidance and autopilot[J]. Chinese Journal of Aeronautics, 2013, 26(3): 741-750.

[15] Guo J G, Zhou J. Integrated guidance-control system design based on H-infinity control[C]//Proceedings of 2010 International Conference on Electrical and Control Engineering, 2010.

[16] Khalil H K. Nonlinear systems[M].USA:Prentice-Hall, 2011.

[17] 王立新. 模糊系统与模糊控制教程[M]. 北京: 清华大学出版社, 2003.

WANG Lixin. A course in fuzzy systems and control[M]. Beijing: Tsinghua University Press, 2003. (in Chinese)

Integrated guidance and control of hypersonic vehicle with fuzzy disturbance observer

ZHAO Tun, WANG Peng, LIU Luhua, WU Jie

(College of Aerospace Science and Engineering, National University of Defense Technology, Changsha 410073, China)

A three-dimensional IGC (integrated guidance and control) approach based on fuzzy disturbance observer was proposed to take advantage of the coupling between the centroid motion, and the attitude motion, and of the uncertainties of a hypersonic vehicle in dive phase as well. An IGC model that can be applied to bank-to-turn control strategy was proposed according to the dynamic equations of the vehicle and the line-of-sight relative motion between the vehicle and the target. The uncertainties in the model were compensated by utilizing the fuzzy disturbance observer, and then an IGC approach was developed by using the block dynamic surface backstepping control method. The states of the closed-loop system were proved to be uniformly ultimately bounded by adopting proper Lyapunov functions. Simulations show that the IGC method is robust to the uncertainties and satisfies the required performance.

hypersonic vehicle; fuzzy disturbance observer; integrated guidance and control; block dynamic surface backstepping control

10.11887/j.cn.201605014

http://journal.nudt.edu.cn

2015-05-26

国防科学技术大学科研计划资助项目(ZDYYJCYJ20140101)

赵暾(1989—)，男，甘肃西和人，博士研究生，E-mail: aero.zhaotun@foxmail.com；吴杰(通信作者)，男，教授，博士，博士生导师，E-mail: wujie_nudt@sina.com

V249.1

A

1001-2486(2016)05-086-08