改进人工蜂群算法在MFAC参数整定中的研究

李荣雨 朱正方

(南京工业大学计算机科学与技术学院，江苏 南京 211816)



改进人工蜂群算法在MFAC参数整定中的研究

李荣雨 朱正方

(南京工业大学计算机科学与技术学院，江苏 南京 211816)

无模型自适应控制是一种针对非线性系统的控制设计方法，其系统参数的整定方法一直是近年的研究热点。为了优化控制器参数，提出了一种基于全局人工蜂群算法的交叉混合全局人工蜂群算法(CGABC)，并把该算法应用到无模型自适应控制(MFAC)中，选取改进误差绝对值积分(ITAE)性能指标作为算法的适应度函数，利用CGABC对MFAC关键参数进行优化及整定。仿真结果证明，与基本人工蜂群算法(ABC)和全局人工蜂群算法(GABC)相比较，MFAC-CGABC控制方法在无扰动的情况下调节时间与超调量都比较出色；当存在扰动时，控制系统依然具有较强的适应性。

人工蜂群算法 无模型自适应控制 参数整定 非线性系统 交叉混合 适应度函数 调节时间 超调量

0 引言

在工业控制中，建立受控系统的状态空间模型有时并不容易，带有不确定性的系统模型在实际应用中可能会出现无法预料的问题[1]。无模型自适应控制(model-free adaptive control，MFAC)可以有效处理带有参数变化和结构变化的非线性系统，但在关键参数的整定、线性化模型的可控性以及伪偏导数或伪梯度的确定等方面还急需解决方案[2-4]。

本文着重研究了无模型自适应控制关键参数的整定问题，通过引入交叉混合的全局人工蜂群算法(cross-mixing global artificial bee colony，CGABC)来平衡算法的探索与开发能力。运用改进误差绝对值积分(integral of time-weighted absolute value of the error，ITAE)性能指标[5]，整定MFAC的四个关键参数，能最大程度地缩短在无扰动状态下MFAC的调整时间，并解决了扰动瞬间超调量过大的问题。通过与基本人工蜂群算法(artificial bee colony，ABC)和全局人工蜂群算法(global artificial bee colony，GABC)对MFAC参数整定的对比仿真，进一步说明了CGABC的有效性。

1 无模型自适应控制系统设计

考虑一类单输入单输出(single input and single output，SISO)离散时间非线性系统：

y(k+1)=f[y(k),y(k-1),...,y(k-ny),

u(k),u(k-1),...,u(k-nu)]

(1)

其紧格式动态线性化数据模型可表示为：

Δy(k+1)=φ(k)Δu(k)

(2)

式中：y(k)和u(k)为控制系统在k时刻的输出与输入；nu和ny为系统阶数；Δy(k+1)、Δu(k)为相邻两个时刻的输出、输入变化；φ(k)为式(1)的伪偏导数(pseudopartialderivative，PPD)。式(2)是式(1)的等价动态线性化表示方式。

1.1 控制算法

考虑加入以下输入准则函数：

J[u(k)]=[y*(k+1)-y(k+1)]2+

λ[u(k)-u(k-1)]2

(3)

式中：λ为权重因子，用来限制输入量的变化,λ>0；y*(k+1)为系统的期望输出。将式(2)代入式(3)，并对u(k)求导，令其等于零，得到如下控制算法[6]：

[y*(k+1)-y(k)]

(4)

式中:ρk为步长因子，使控制算法更具有一般性；λ可限制控制输入Δu的变化。

1.2 PPD估计算法

为实现式(3)的控制算法，需要已知PPD的值，由于系统模型未知，PPD的精确真实值很难获取，因此需要利用受控系统的输入、输出数据设计其估计算法。为防止参数估计值对不准确的采样数据过于敏感，加入以下估计准则函数[7]：

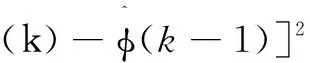
(5)

对式(5)中的φ(k)求极值，得PPD估计算法为：

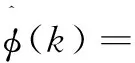
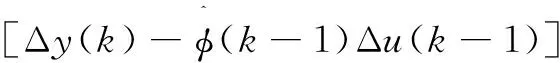
(6)

2 基于CGABC的无模型自适应控制系统

在使用无模型自适应控制方法时，参数的选取对控制系统影响明显。因此，采用优化算法对式(5)和式(6)中的步长因子ρk、ηk，权重因子λ、μ进行参数整定。通过交叉混合的全局人工蜂群算法整定参数后，控制系统的超调量减小，调节时间减少，并最终达到稳定状态。基于CGABC的MFAC参数整定原理如图1所示。

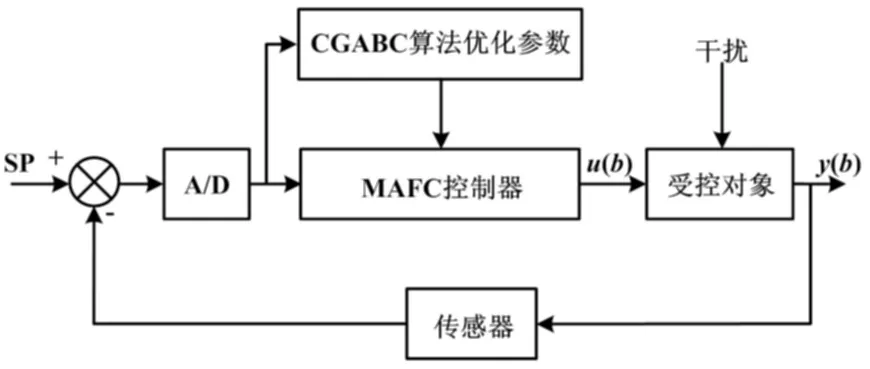
图1 CGABC-MFAC参数整定原理框图

在基本人工蜂群算法中，存在三种蜜蜂——采蜜蜂、观察蜂及侦查蜂。采蜜蜂负责采集蜂蜜和招募蜜蜂；观察蜂负责按照一定规则选择采蜜蜂进行跟随；侦查蜂负责随机地搜索新蜜源。采蜜蜂按照式(7)进行邻域搜索。

vij=xij+α(xij-xkj) i≠k

(7)

式中:xij为第i个解的第j个坐标；xkj为第k个解的第j个坐标，k在领域内随机生成；vij为新解；α为邻域搜索系数，为-1～1的随机数。按照贪婪准则式(8)替换蜜源。观察蜂按照式(9)、式(10)计算跟随概率，选择采蜜蜂进行跟随，转化为采蜜蜂进行邻域搜索。

(8)

(9)

(10)

式中:fv、fx为vi、xi的适应度值；fi为函数值;fitnessi为函数适应度值;pi为第i只观察蜂跟随概率。

式(7)决定了人工蜂群算法在接近全局最优时，存在搜索速度变慢、过早收敛以及陷入局部最优解的问题。Zhu和Kwong提出了一种全局最优引导的人工蜂群算法[8],参照粒子群算法将全局最优项加入到人工蜂群搜索公式，从而提高算法开发能力。Zhang采用类似的方法[9]，在每次迭代中随机取较优值中的一个作为全局最优值。Abdul在迭代算法过程中，不仅引入了当前全局最优值，还引入了当前全局次优值[10]。Guo将粒子群算法公式中的全局社会项增加到人工蜂群算法中，构建了全局人工蜂群搜索算法[11]，其与粒子群算法相似，但算法复杂性更高。GABC算法的搜索式如式(11)所示：

(12)

采蜜蜂邻域搜索后与全局最优值进行交叉操作,提高了人工蜂群算法的开发能力。为了增加算法的搜素能力，建立了式(13)。

(13)

通过系数cr来协调算法的探索能力和开发能力，选取四个测试函数判断cr取值对优化结果的影响。测试函数如表1所示。

表1 测试函数表

采用不同极值点的测试函数，对优化算法中不同的cr取值进行对比。算法的优化精度对比如图2所示。

肝动脉造影显示血管瘤供血动脉稍增粗迂曲， 或可见大小不等的“树上挂果征”或者“早出晚归”的血管湖征，供血动脉注入平阳霉素碘化油乳剂之后，有不同程度碘化油在病灶中沉积，并且有肿瘤轮廓的显现，其分布区域的形状大小与部位等与血管造影一致。肝动脉栓塞之后进行动脉造影显示流体血窦及供血动脉完全闭塞，肿瘤没有显影。所有病例中14例栓塞一次成功，有5例患者共行2次介入栓塞治疗，2例患者行3次介入栓塞治疗。

图2 优化精度对比图

由图2可知，当cr取值为0.6时，无论测试函数极值点为多少，算法优化性能结果稳定性都较好。

2.2 CGABC算法参数的选取

基于改进人工蜂群算法的空压机压力控制，利用交叉混合的全局人工蜂群算法对MFAC控制器的参数ρk、ηk、λ和μ进行优化及整定。选取采蜜蜂和观察蜂数量各为20，最大迭代次数为100。步长因子ηk和权重因子μ的搜索范围取决于它们对控制器的影响。步长因子ηk越大，系统的响应速度越快，但会增大超调，影响稳定时间；反之，系统的响应速度变慢，超调量降低。缩小权重因子可以减少系统的响应时间；但过小则会引起系统震荡，导致调节时间延长。CGABC算法的参数选择如表2所示。

表2 CGABC算法参数值

2.3 交叉混合人工蜂群算法的参数整定步骤

CGABC算法在收敛速度和收敛精度上的良好表现，为MFAC参数整定提供了理论依据。其步骤可以简单地描述为:

①初始化蜜蜂种群。蜜蜂总数为N(采蜜蜂、观察蜂各N/2)；最大搜索次数为limit；迭代次数iter=0，最大迭代次数为maxCycle。所有蜜蜂均为侦查蜂模式，随机产生N个可能解，并通过适应度函数计算出最小函数值。

②每只采蜜蜂利用式(7)局部搜索新蜜源，根据rand与系数cr的比较情况来判断是否根据式(13)进行交叉混合，然后根据贪婪算法保留最优值。

③利用式(9)和式(10)计算每只采蜜蜂被选择的概率，概率值越大的采蜜蜂，被观察蜂跟随的可能性越大。

④观察蜂转化为采蜜蜂后，再次进行邻域搜索，经系数cr判断后，选择是否交叉混合，并按照贪婪法则选择新解。

⑤当采蜜蜂在蜜源附近寻找次数超过limit时，转化为侦查蜂，并随机寻找新蜜源。

⑥确定本次循环的最小目标函数值，若优于之前得到的全局最小目标函数值，则将它赋值给全局最小目标函数值，并记录对应的全局最优解向量。

⑦若未达到最大循环迭代次数，转到步骤②；否则，循环结束，得到最优的控制参数。

交叉混合人工蜂群算法流程图如图3所示。

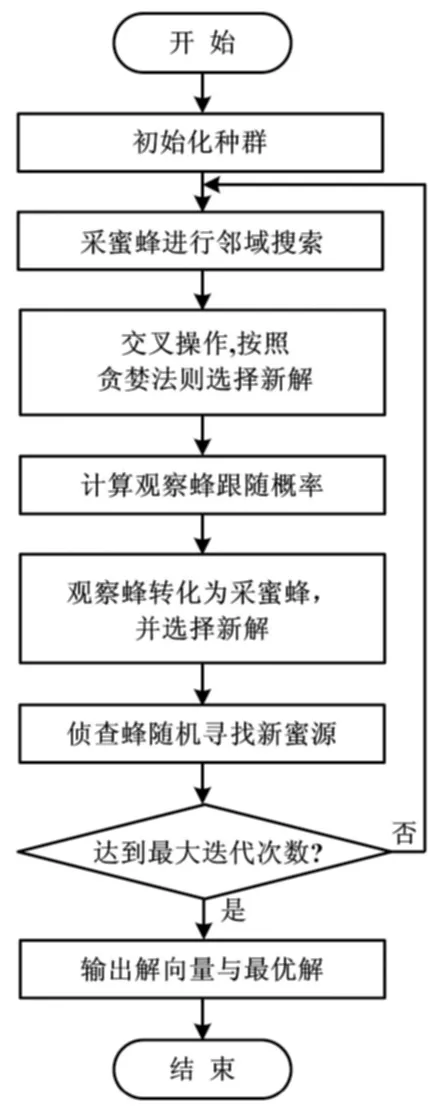
图3 CGABC算法流程图

2.4 适应度函数的确定及改进

在优化及控制过程中，无论在无扰动还是定值扰动情况下，为了最大程度地优化控制效果，应选取合适的适应度函数。ITAE性能指标充分考虑了时间因素，能够降低系统初始大误差的影响，调节时间短，具有较好的选择性和适应性。但是，其在上升时间、稳态误差和控制量这三个方面仍存在不足[12]。为了防止控制能量过大而导致系统不稳定的问题,且MFAC本身具备消除稳态误差的能力，本文在目标函数中加入控制量、上升时间和超调量作为综合约束条件,采用式(14)作为参数选取的适应度函数：

(14)

式中:e(t)为系统误差；u(t)为控制器输出；tu为上升时间；w1、w2为权值。采用惩罚机制控制超调量，产生超调后，将超调量作为指标中的一项，适应度函数为：

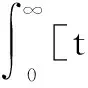
w3ey(t)]dt+w2tu

(15)

式中:w3是为了消除超调过大而加入的权值；ey(t)=y(t)-y(t-1)；u(t)为被控对象的输出；w1、w3的选取可视具体情况而定[13]，根据优化的侧重点，适当地调整其对应的权值。为了对控制量和超调量进行优化，本文选取[w1,w2,w3]=[0.01,2,20]。即MFAC的适应度函数选取为：

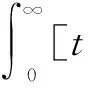
20ey(t)]dt+2tu

(16)

综上所述， 利用改进的ITAE性能指标作为适应度函数，在充分考虑系统调节时间的基础上，考虑其控制量和超调量，以适应MFAC的控制需求。

3 仿真验证

由图4可知，经过100次迭代后，参数ρk、λ、ηk、μ的最优解分别为39.001、0.01、25.232 6、28.340 4。

将参数代入构造的无模型自适应控制器中，得到空压机出口压力模型在三种控制算法的无扰动仿真结果，如图5所示。

由图5可知，在无扰动情况下，三种控制算法的稳态精度都很好。以2%为允许误差范围，MFAC-CGABC的控制调节时间ts为130s、峰值时间tp为50s、超调量σp为20%；MFAC-GABC的ts为140s、tp为44s、σp为28%；MFAC-ABC的ts为143s、tp为47s、σp为28%。由数据可知，MFAC-CGABC的调节时间最短，超调量最小。虽然响应速度稍慢，但从整体的控制性能来看，MFAC-CGABC控制具有良好的效果。详细的性能指标见表3。

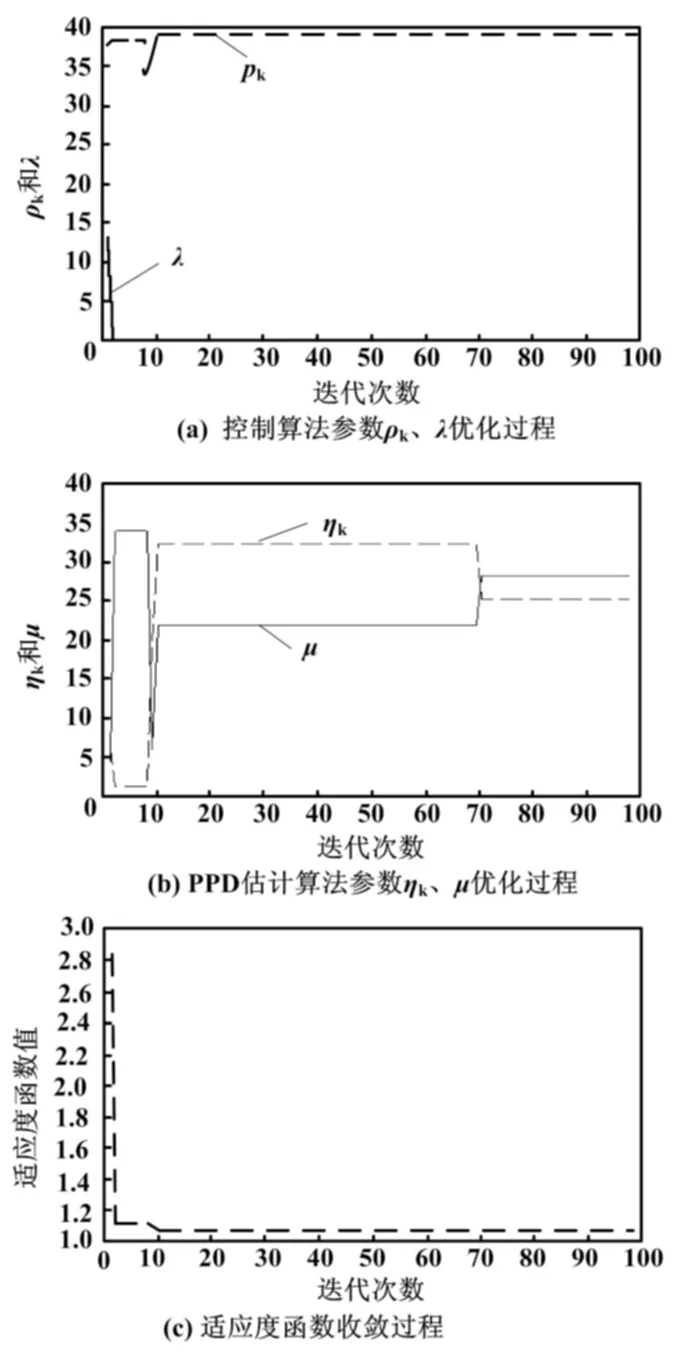
图4 参数优化整定结果

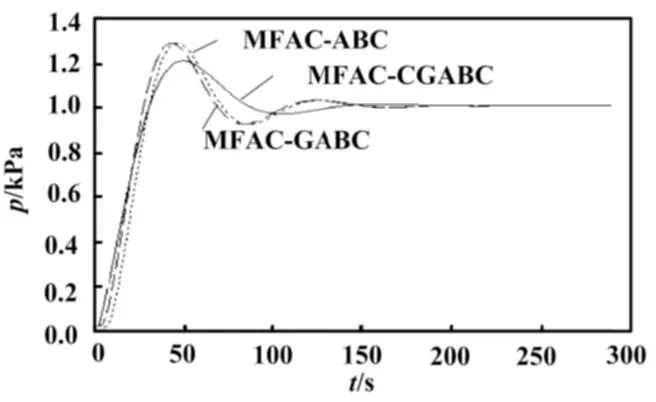
图5 无扰动下三种控制算法的仿真结果

算法ts/stp/sσp/%MFAC-ABC1434728MFAC-GABC1404428MFAC-CGABC1305020

在250 s时加入定值扰动，相应的控制曲线也有变化，调整后的控制曲线如图6所示。

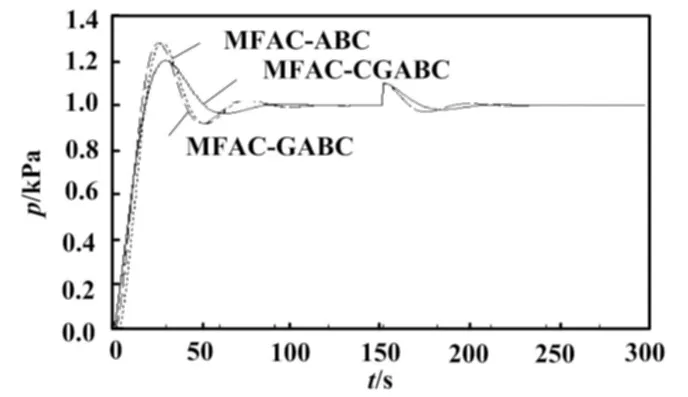
图6 扰动情况下三种控制算法的仿真结果

由图6可知，加入扰动后MFAC-CGABC控制调节时间为323 s；MFAC-GABC的ts为352 s,MFAC-ABC的ts为352 s。由数据可知，在定值扰动下，MFAC-CGABC控制具备良好的稳定性，能有效减少震荡的产生，并能在短时间内恢复稳定，具有较强的鲁棒性。

4 结束语

本文针对无模型自适应控制中参数整定的问题，提出MFAC-CGABC。针对MFAC-CGABC，设计了改进的ITAE适应度函数，使用Matlab/Simulink搭建了控制系统模型并进行了仿真。由仿真结果可知，基于交叉混合人工蜂群的无模型自适应控制具有超调量小、调节时间短、鲁棒性强等优势，同时有良好的稳定性和稳态精度，控制效果理想。

[1] ANDERSON B D O,DEHGHANI A. Challenges of adaptive control-past,permanent and future[J]. Annual Reviews in Control,2008,32(2):123-135.

[2] XU J X,HOU Z S. Notes on data-driven system approaches[J]. Zidonghua Xuebao/acta Automatica Sinica,2009,35(6):668-675.

[3] HOU Z,ZHU Y. Controller dynamic linearization based model free adaptive control for discrete-time nonlinear systems[J]. IEEE Transactions on Industrial Informatics,2013,9(4):2301-2309.

[4] XU D,JIANG B,SHI P. A novel model-free adaptive control design for multivariable industrial processes[J]. IEEE Transactions on Industrial Electronics,2014,61(11):6391-6398.

[5] 王晶，纪超，曹柳林，等.基于二阶泛模型的无模型自适应控制及参数整定[J].中南大学学报,2012，5(5):1795-1802.

[6] 王卫红，侯忠生，霍海波，等.基于数据驱动方法的控制器设计及其参数整定[J].系统科学与数学，2010，6(30):792-805.

[7] 翁永鹏,高宪文,吕明阳. 一类非仿射非线性离散系统的改进无模型自适应控制[J]. 控制与决策,2014(12):2226-2234.

[8] ZHU G,KWONG S. Gbest-guided artificial bee colony algorithm for numerical function optimization[J]. Applied Mathematics & Computation,2010,217(7):3166-3173.

[9] ZHANG S,LIU S. A novel artificial bee colony algorithm for function optimization[J]. Mathematical Problems in Engineering,2015:1-10.

[10]ABRO A G,Mohamad S J. Enhanced global-best artificial bee colony optimization algorithm[C]//2012 Sixth UKSim/AMSS European Symposium on Computer Modeling and Simulation

(EMS).IEEE,2012:95-100.

[11]GUO P,CHENG W,LIANG J. Global artificial bee colony search algorithm for numerical function optimization[C]//2011 Seventh International Conference on Natural Computation (ICNC). IEEE,2011:1280-1283.

[12]赵文龙,齐柳. 基于ITAE指标等概率分布的PID参数整定[J]. 电子技术与软件工程,2015(8):95-97.

[13]JIAN X X. A survey on iterative learning control for nonlinear systems[J]. International Journal of Control,2011,84(7):1275-1294.

Research on the Parameter Tuning Based on Improved ABC Algorithm for MFAC

Model free adaptive control (MFAC) is a control design method for nonlinear system,recently,the tuning method of parameters in the system becomes a hot research topic. In order to optimize the parameters of the controller,a cross-mixing global artificial bee colony (CGABC) algorithm based on the global artificial bee colony (GABC) algorithm is proposed,and the algorithm is applied in the model free adaptive control. The improved integral of time-weighted absolute value of the error(ITAE) performance index is selected as the fitness function of the algorithm，and the key parameters of the model free adaptive control are optimized and tuned by using CGABC. The simulation results prove that comparing with artificial bee colony(ABC) and global artificial bee colony(GABC),the regulation time and overshoot of MFAC-CGABC are better under the conditions without disturbance,and the control system still has strong adaptability under disturbance.

Artificial bee colony algorithm Model free adaptive control Parameter turning Nonlinear system Cross mixing Fitness function Adjusting time Overshoot

李荣雨(1977—)，男，2007年毕业于浙江大学控制科学与工程专业，获博士学位，副教授；主要从事工业系统的监控与先进控制的研究。

TH-39;TP273

A

10.16086/j.cnki.issn 1000-0380.201608019

修改稿收到日期：2016-03-08。