多源信息融合的航空部附件状态退化预测
李文峰 许爱强 陈 涛 韩广民
(海军航空工程学院科研部1,山东 烟台 264001;92635部队2,山东 青岛 266000)
多源信息融合的航空部附件状态退化预测
李文峰1,2许爱强1陈 涛2韩广民2
(海军航空工程学院科研部1,山东 烟台 264001;92635部队2,山东 青岛 266000)
针对航空部附件状态退化预测问题,提出了一种经验模态分解(EMD)和自组织特征映射(SOFMs)量化误差模型相结合的部附件退化趋势预测方法。采集部附件多个特征指标的状态监测信息,运用EMD提取包含微弱信号的特征信息,并消除部分噪声干扰;运用SOFMs实现多源传感器信息融合,并建立最小量化误差(MQE)模型,量化部附件运行状态,以实现部附件的状态退化预测。通过对某型航空陀螺仪的仿真验证表明,EMD-SOFMs量化误差模型能够有效、准确地提取陀螺仪状态信息,融合量化陀螺仪运行状态,实现陀螺仪的状态退化预测。
经验模态分解 自组织特征映射 误差模型 航空陀螺仪 多源传感器 预测 特征提取 信息融合
0 引言
随着航空部附件的复杂化、综合化及信息化,对航空装备的安全可靠性要求不断提升。为进一步提高飞机战备完好率和任务成功率,可根据航空部附件性能状态的退化预测,对其潜在故障采取预防性维修措施。
相对单源信息来说,多源传感信息能够获得更有效的状态退化表征信息,提高状态退化预测的准确性[1-2]。文献[3]利用隐马尔可夫模型(hidden Markov model,HMM)实现陀螺仪多源传感信息的故障预测,但其将多源传感信息直接作为输入,没有考虑各参数的进一步特征提取。本文针对一类航空部附件,其具备能够表征累计损伤或状态渐进退化的可监测参数,采用自组织特征映射(self-organizing feature maps,SOFMs),对经验模态分解(empiricat mode decomposition,EMD)特征提取后的指标进行融合预测,构建量化误差模型,通过最小量化误差(minimum quantization error,MQE)值,直观表征航空部附件的状态退化趋势。
1 航空部附件状态退化问题描述
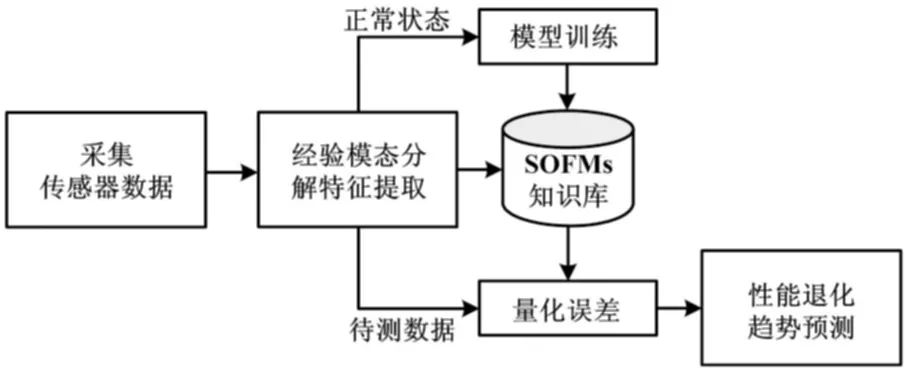
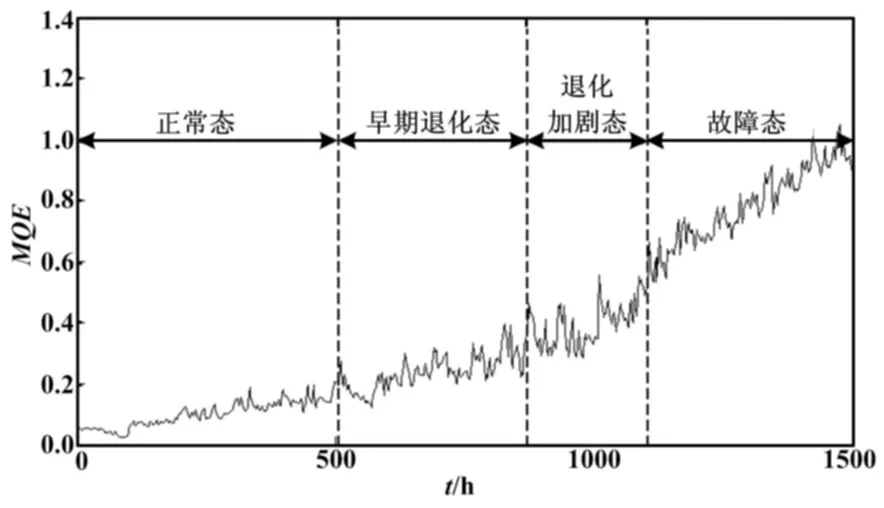
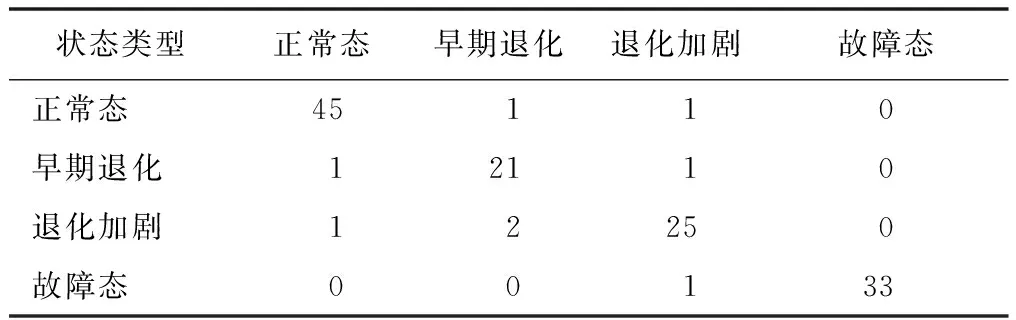
针对具备渐变累积损伤特点的航空部附件,其性能状态退化是指航空部附件在实际运行使用中,因受使用环境中各种应力的持续累计作用,而出现疲劳损伤、老化、松动、锈蚀及应力变形等物理或化学意义上的性能退化。这种性能退化从量化角度来考虑,表现为航空部附件的性能参数逐渐偏离正常范围。性能参数通常指能够直接或间接表征部附件性能退化的某个或某几个可量测特征指标,称为航空部附件的性能变量。航空部附件的性能退化最终结果为航空部附件出现严重故障或完全损坏不可维修,因此需在其完全损坏前把握性能状态的变化过程。图1描述了航空部附件状态退化曲线,以时间轴t为横轴,以性能变量M为纵轴。M的取值为0≤M≤1。当M=1时,表示部附件状态完好无损;当0 图1 航空部附件状态退化曲线图 由图1可知,航空部附件性能分为四个状态。 ①正常态。正常态是指部附件从M=1时开始,一直到“部附件故障检测点P”时的状态。此时,航空部附件在运行过程中,性能变量也在发生变化,但没有超出相应正常值范围,能够很好地完成部附件所执行的任务。从定量角度来说,即0.9 ②早期退化态。早期退化态是指部附件从“部附件故障检测点P”开始一直到“部附件当前状态点T”时的状态。此时,航空部附件在运行过程中,性能变量继续减小,部附件的工作性能与正常态时的性能存在偏差,但依然能完成所执行的任务。从定量角度来说,即0.8 ③退化加剧态。退化加剧态是指部附件从“部附件当前状态点T”开始一直到“部附件功能故障点F”时的状态。此时,航空部附件在运行过程中,性能变量持续减小,部附件的工作性能部分失效,能够部分完成所执行的任务,这也是剩余使用寿命预测的时间段。从定量角度来说,即0.6 ④故障态。故障态是指部附件从“部附件功能故障点F”开始一直到M=0.2时的状态。此时,航空部附件在运行过程中,性能变量继续减小,部附件的工作性能失效,不能够完成所执行的任务。从定量角度来说,即0.2≤M≤0.6;从定性角度来说,部附件在故障态的性能表现为“差”。 由上述分析可以看出,如果能得到航空部附件的性能变量,就能分析预测航空部附件的状态退化。如果存在能够直接表征部附件状态退化的性能变量,即可直接对其进行监测并采集数据;当没有可以直接表征状态退化的性能可观测变量时,可以采用能够间接表征状态退化的多个特征指标,融合表达性能变量,从而达到预测状态退化的目的。这也是本文进行状态退化预测的思路。 2.1 EMD基本原理 1998年,美国国家航空航天局(NASA)的NordenE.Huang提出了EMD方法[4-7]。EMD的提出源于Hierbert变换的研究。Hierbert变换是一种实用的信号分析方法,然而,Hierbert变换的先决条件限制了该方法的应用,而EMD信号分解能够满足Hierbert变换的先决条件。因此,通常将EMD和Hierbert变换称为Hierbert-Huang(HHT)变换。信号首先经EMD分解成有限个成分,然后通过Hierbert变换实现信号的时频分析。 HHT利用EMD将信号分解成一组固有模态函数(intrinsicmodefunction,IMF),IMF是任何复杂信号的组成成分。不同于传统的信号分析方法,如傅里叶变换、小波分析等,EMD的信号分解是一个自适应的过程,无需预先设定滤波器或像傅里叶变换需线性或平稳信号。因此,HHT是一种对非线性非平稳信号有效的自适应时频分析方法。实践证明,HHT的应用范围越来越广泛。 虽然固有模态函数是信号的基本组成成分,不同于简单的单调调和函数,其振幅和频率是可变的。瞬时频率是由固有模态函数的Hierbert变换而来的,而在将信号分解成IMF方面,Huang等提出了经验模态分解方法,EMD的具体分解步骤如下。 步骤(1):将原始信号x(t)看作数据序列,操作如下。 ①确定所有的极值(包括极大值和极小值)。 ②利用三次样条函数在极小值之间进行插值,得到下包络线emin(t)。 ③采用与步骤②相同的方法,得到上包络线emax,x(t)的所有数据应被上下包络线所包含,计算均值: m1(t)=[emax(t)+emin(t)]/2 (1) 步骤(2):从原始序列x(t)中减掉m1(t),得到数据序列h1(t)。 h1(t)=x(t)-m1(t) (2) 验证h1(t)是否满足成为IMF的两个条件。如果h1(t)不是IMF,将h1(t)作为数据序列,重复步骤(1)的计算,得到新的序列h2(t): h2(t)=h1(t)-m2(t) (3) 验证h2(t),重复步骤(1)直到k时刻,此时hk(t)为一个IMF。 将hk(t)作为第一个IMF,令: c1(t)=hk(t) (4) 步骤(3):从原始序列x(t)中减掉c1(t),得到差值分量r1(t)。 r1(t)=x(t)-c1(t) (5) 将差值分量r1(t)作为一个新的数据序列。 步骤(4):迭代计算步骤(1)~(3),得到新的IMF,分别为c2(t),c3(t),…,cn(t),直到残余分量rn(t)至少满足以下三个条件中的一个。①rn(t)为一个单点函数;②rn(t)只有一个极值;③rn(t)为常数。 此时,终止迭代计算过程,得到所有的固有模态函数和最后的残余分量rn(t)。原始数据序列x(t)可以表示为所有IMF和rn(t)的和: (6) 需要说明的是,在迭代过程中,极值的数量越来越少,而极值之间的时间间隔越来越大。在每一次分解时,均产生一个IMF和残余分量,分解后的IMF为高频分量,而残余分量的频率则低于同时分解出来的IMF。 2.2 多源信息特征提取 部附件经验模态分解具体流程为:采集部附件状态监测信息,将各传感器采集到的数据进行数据预处理,包括数据的剔除和补缺;然后进行归一化处理,即数据的无量纲化;最后利用EMD提取出各个特征的合理特征因子,由于EMD具备提取微弱信号的优势,并不会消除所有噪声。 3.1 自组织映射理论 1981年,芬兰人Kohonen首次提出了SOFMs。自组织映射使用一种无监督的学习方法,将高维数据映射到一维、二维或三维数据空间,且保持了原空间的拓扑性质[8-10]。SOFMs的一个主要优点是,通过自组织特征映射产生的聚类,在保留输入空间的底层结构的同时降低了空间维数。输入模式向量的概率密度函数p(x)以权重矢量的形式表达,从而得到神经元映射。 SOFMs主要包括输入层和输出映射两个部分。输入层的维数不受限制,而受拓扑有序的约束;输出映射的维数为一维、二维,至多三维。如果一个n维输入矢量被定义为: x=[x1,x2,…,xn]T (7) 则m个神经元中的每一个均对应一个权重矢量,表示为: ωi=[ωi1,ωi2,…,ωin]T (8) 式中:i=1,2,…,m。 由此可见,输入矢量和权重矢量有相同的维数。 SOFMs神经网络优先学习输入和输出节点之间的权重值。通常情况下,可随机初始化权重值以证明SOFMs强大的自组织能力。实践证明,如果初始化权重值呈线性关系,则SOFMs的计算相当快。在SOFMs近似组织的初期,一个较窄的邻域函数和较小的学习速率因子可初步设定。 学习过程是一种竞争性学习,只有竞争力较大的神经元及其邻近神经元,才会在学习过程中被更新。获胜的输出神经元由一种相似性度量决定,它可以是欧氏距离度量或两个向量的点积,最简单的测量距离是欧几里得距离测度。最小距离测度定义了在输出层中的最佳匹配神经元(best match unit,BMU),BMU是一个权重矢量和输入矢量有最小测量距离(比如欧几里得距离测度)的神经元。因此,xTωi的平方根被用于计算x和ωi之间的距离。输入矢量的最好匹配单元ωc满足以下公式: ‖x-ωc‖=min{‖x-ωi‖} (9) 式中:“‖ ‖”用于计算输入向量和神经元距离;i=1,2,…,m。 在SOFMs训练过程的每一步,BMU的权重或者在输入向量周围预先定义范围的神经元有以下公式更新: wi(t+1)=wi(t)+Nmi(t)[x(t)-ωi(t)] (10) 式中:wi为权重;t为迭代步数;x(t)为t时刻的输入向量;Nmi(t)为关于最佳匹配神经元m的邻域函数。邻域函数可以为高斯函数: (11) 式中:rm为最佳匹配神经元向量;ri为最佳匹配神经元相邻神经元向量;α(t)为学习速率,0<α(t)<1,随时间单调减小;σ(t)为领域函数的宽度,随时间单调减小。由上述分析可以看出,BMU权重矢量变化最大,而离BMU距离越远的神经元变化越小。 3.2 最小量化误差模型 在一个SOFMs训练结构中,输入向量和BMU权重的距离被用作表达退化状态的测量值。定义输入向量与BMU权重之间的距离为最小量化误差(minimum quantization error,MQE)[11]: MQE=‖x-WBMU‖ (12) 式中:x为输入向量;WBMU为BMU的权重向量。 正常状态的数据被用于训练一个SOFMs结构作为基准。后来采集到的数据被用于作为输入量代入SOFMs结构。得到所有的MQE后,输入向量与基准相比的偏差能够作为状态退化的性能变量。如果输入向量接近基准,MQE较小;否则,较大的MQE表示偏离基准,这意味着可能存在一个退化或不正常的状态。利用这种方法,多维特征空间被转化为表示退化状态的距离测量值——MQE。同时根据在线新采集到的数据,代入到SOFMs知识库后,从一系列的MQE趋势中,找到数据段在MQE中的位置,从而能够预测设备所处的状态以及后来的退化趋势。 3.3 退化趋势预测 根据部附件正常工作时各性能指标的范围,选取部附件在正常状态下的各指标观测数据,经特征提取后代入模型训练。图2给出SOFMs量化误差模型趋势预测流程。 图2 退化趋势预测流程图 给定SOFMS知识库后,对待测数据进行数据处理和特征提取,建立最小量化误差模型,得到MQE;通过MQE计算后,得到部附件的退化趋势和性能退化评估结果。 4.1 航空陀螺仪状态退化描述 选取某型航空陀螺仪,对本文提出的方法进行仿真验证。作为一种高速旋转的复杂精密设备,航空陀螺仪运行过程经历了正常状态、早期退化状态、退化加剧状态及故障状态。在航空陀螺仪的退化过程中,并没有某个观测值能直接表示陀螺仪的退化过程,所以需要可测量值的融合信息来反映评估陀螺仪的运行状态。 4.2 信号采集及预处理 航空陀螺仪性能指标数据的采集是航空陀螺仪退化趋势预测研究的重要基础。对航空陀螺仪进行退化趋势预测,必须长期采集并实现航空陀螺仪振动、温度、随机漂移、电源电压、电机功率等性能指标的数据存储。采集陀螺仪运行状态的数据后,需要从信号中提取能够表达陀螺仪性能状态的特征因子,这是进行陀螺仪退化趋势预测的关键。特征因子选择的准确度决定了陀螺仪退化趋势的预测精度。本文采用EMD对振动、温度、随机漂移、电源电压、电机功率等参数进行分析,通过对陀螺仪采集到的数据信息进行经验模态分解,提取表征陀螺仪运行状态的特征因子。由于外部环境的噪声干扰也将影响退化趋势的预测精度,在提取早期故障微弱信号的同时,针对陀螺仪自身及采集过程的特点,利用EMD消除部分噪声干扰。 4.3 性能状态特征提取 在试验室条件下,对四台某型航空陀螺仪的各性能指标(包括陀螺仪振动信号、温度、随机漂移、电源电压、电机功率)进行数据采集。采集过程为:由运行的正常状态开始,经历一系列退化状态,最终到达故障状态。每一秒代表一个周期,即一次,共采集样本1 498次。 样本数据经过EMD特征提取,选择合适的IMF模态作为SOFMs神经网络的输入。 4.4 退化趋势预测分析及验证 将4.1节提取的陀螺仪正常状态的13个IMF作为特征值输入到SOFMs量化误差模型进行训练,得到正常状态的最小量化误差;然后将陀螺仪从正常态到故障态的退化数据输入到量化误差模型,得到最小量化误差序列。由于EMD采集微弱信号特征信息时,没有完全消除噪声干扰,因此,采用小波包降噪[12]得到陀螺仪的性能变量MQE表达如图3所示,并依据退化曲线均值和平均斜率划分陀螺仪的各个状态。 图3 小波包降噪后陀螺仪退化趋势示意图 采集并随机选取陀螺仪132个状态(每个状态记录1 s的数据)的测试数据,生成观测数据后,输入到SOFMs量化误差模型进行验证。退化趋势均值即为陀螺仪当前的运行状态,预测各个状态的结果如表1所示。 表1 退化趋势预测结果 由表1可以计算出退化趋势预测的准确率达到94%。综上所述,采用EMD与SOFMs量化误差模型相结合的退化趋势预测方法,能够较真实地反映陀螺仪所处的状态,从而验证了该方法在陀螺仪退化趋势预测中的有效性。 本文采用EMD-SOFMs量化误差模型采集陀螺仪正常状态的信号。与小波包分解信号相比较,EMD方法能够提取微弱信号的特征因子,并消除部分噪声干扰;与单源信息表征设备状态相比较,SOFMs方法能够实现多源传感器信息融合;结合陀螺仪不同状态特征信息,可建立最小量化误差模型,得到性能变量MQE,从而量化陀螺仪运行状态,实现陀螺仪的退化趋势预测。实例分析及验证表明,EMD-SOFMs量化误差模型能够有效准确提取陀螺仪状态信息,融合量化陀螺仪运行状态,预测陀螺仪退化趋势,为陀螺仪维护决策提供依据。但是,EMD方法在提取早期故障微弱信号的同时,并不能完全消除噪声干扰,退化趋势的 预测精度还有待提高。 [1] 王华伟,吴海桥.基于信息融合的航空发动机剩余寿命预测[J].航空动力学报,2012,27(12):2749-2755. [2] RONALD R,YAGER. Life fellow set measure directed multi-Source information fusion[J]. IEEE Transactions on Fuzzy Systems,2011,19(6):1031-1039. [3] 尚永爽,许爱强,吴忠德. 基于SOFM神经网络和HMM的动调陀螺仪故障预测方法研究[J]. 机械科学与技术,2012,31(10):1711-1715. [4] 沈毅,张筱磊,王振华.基于EMD和有向因子图的航天器故障诊断[J].哈尔滨工业大学学报,2013,45(1):19-24. [5] 张超,陈建军,姚建刚,等.基于EMD分解和奇异值差分谱理论的轴承故障诊断方法[J].振动工程学报,2011,24(5):540-545. [6] WU Z,HUANG N,LONG S,et al. On the trend detrending and variability of nonlinear and nonstationary time series[J]. Proceedings of the National Academy of Sciences,2007,104(38):14889-14894. [7] 苏文胜,王奉涛,张志新,等.EMD降噪和谱峭度法在滚动轴承早起故障诊断中的应用[J].振动与冲击,2010,29(3):18-21. [8] 邹云峰,吴为麟,李智勇.基于自组织映射神经网络的低压故障电弧聚类分析[J].仪器仪表学报,2010,31(3):571-576. [9] 谢涛,何怡刚,姚建刚,等.基于小波包和自组织网络的模拟电路故障诊断[J].微电子学,2009,39(2):190-193. [10]LI H,WANG Z,KANG Y,et al. Research on tracing aircraft assembly error source based on SPC and SOFM[C]//2015 International Conference on Automation,Mechanical Control and Computational Engineering. Atlantis Press,2015. [11]LIAO L X. An adaptive modeling for robust prognostics on a reconfigurable[C]//The Cincinnati city:The university of Cincinnati in the college of engineering,2010. [12]刘爱平,邹立华,戴素亮,等.振动控制研究中的小波包降噪处理[J].振动与冲击,2008,27(2):95-98. Predicting the Status Degradation of Aviation Accessories Based on Multi-source Information Fusion For predicting the status degradation of aviation accessories,the method combining empirical mode decomposition (EMD) and self-organizing feature maps (SOFMs) quantization error model is put forward. The status monitoring information about multiple feature indexes of accessories is collected; by using EMD,the feature information containing weak signals is extracted,and partial noise interference is eliminated. Multi-source sensor information fusion is realized through SOFM,and the minimum quantization error (MQE) model is established; to quantify the running status of accessories and implement prediction of status degradation of accessories. A certain type of aviation gyroscope is selected for conducting simulation and verification. Examples of analysis and verification show that EMD-SOFMs quantization error model does effectively and precisely extract the status information of gyroscope,fuse and quantify operating status of gyroscope,and implement the prediction of status degradation for gyroscope. Empirical mode decomposition Self-organizing feature maps Error model Aviation gyroscope Multi-source senser Prediction Feature extraction Information fusion 李文峰(1983—),男,现为海军航空工程学院军事装备学专业在读博士研究生;主要从事航空装备故障预测与综合保障的研究。 TH13;TP206 A 10.16086/j.cnki.issn 1000-0380.201608007 修改稿收到日期:2015-09-23。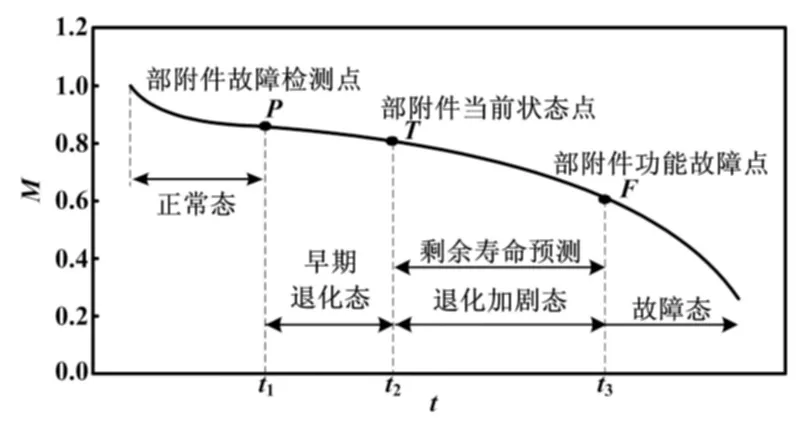
2 基于EMD的多源信息特征提取
3 基于SOFMs量化误差模型的状态退化预测
4 实例分析
5 结束语

