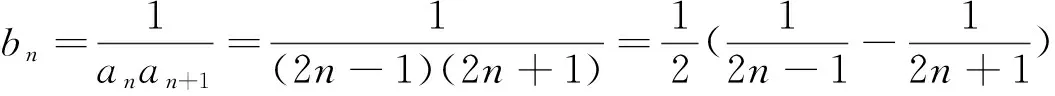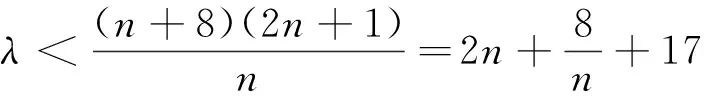例析数列中几道常见的分类讨论问题

浙江省绍兴市鲁迅中学 (312000)

钟杰伦



例析数列中几道常见的分类讨论问题

浙江省绍兴市鲁迅中学 (312000)

钟杰伦

分类讨论思想是高中数学的一种重要的思想，也是历年高考的考查重点．在解决数列问题的过程中,涉及到分类讨论的题目时常出现.下面总结几例予以说明.

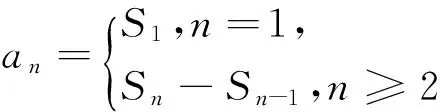
例2 已知数列{an}中,a1=1,a2=2,且an+1=(1+q)an-qan-1(n≥2且q≠0).

(1)设bn=an+1-an(n∈N*),证明:数列{bn}是等比数列;

(2)求数列{an}的通项公式.

解析:(1)∵an+1=(1+q)an-qan-1,∴an+1-an=q(an-an-1),即bn=bn-1,∴数列{bn}是以q为公比,b1=a2-a1=1为首项的等比数列.

评析:此题的易错点在于对公比q的讨论,等比数列的前n项和问题往往会出现公比q为参数的情形,此时讨论公比q是否可以等于1就是解决题目的关键.

(1)求a1、d和Tn；

(2)若对任意的n∈N*，不等式λTn

评析:数列问题中,经常会出现(-1)n的形式,当数列通项公式中出现(-1)n的形式时,往往对n分奇、偶讨论,问题就迎刃而解了.

例4 数列{an}是递增的等差数列，且a1+a6=-6，a3·a4=8．

(1)求数列{an}的通项公式；

(2)求数列{|an|}的前n项和Tn．

得a3、a4是方程x2+6x+8=0的二个根x1=-2,x2=-4，又此等差数列为递增数列，∴a3=-4,a4=-2，∴公差d=2,a1=-8，∴an=2n-10.

(2)由an≥0得2n-10≥0，解得n≥5，此数列前四项为负的，第五项为0，从第六项开始为正的．当1≤n≤5且n∈N*时，Tn=|a1|+|a2|+…+|an|=-(a1+a2+…+an)=-Sn=-n2+9n.当n≥6且n∈N*时，Tn=|a1|+|a2|+…

+|a5|+|a6|+…+|an|=-(a1+a2+…+a5)+(a6+…+an)=Sn-2S5=n2-9n+40.

评析:此题的关键在于求数列{|an|}的前n项和Tn时，需考虑去绝对值的条件时应注意对相应n范围的讨论．

(1)求Sn;

评析:这是一道典型的分组求和问题．当数列{an}的通项公式中带有正弦、余弦等三角形式时，往往可先考虑三角式的周期，然后再按三角式的周期进行分组求和．当然，这类题往往也可运用并项求和方法求解．