几道2016年国际数学奥林匹克试题求解之深度思考
2016-11-25 06:12:58江西省上饶市鄱阳中学333100
中学数学研究(江西) 2016年11期
江西省上饶市鄱阳中学 (333100)
王运良
几道2016年国际数学奥林匹克试题求解之深度思考
江西省上饶市鄱阳中学 (333100)
王运良
解题不是一蹴而就的事.要善于学习,勤于总结.从本文所选例题的证明来看似乎简单容易,其实不然,每道题的求解都是经过精心思考、细致打磨出来的,都饱含着解题者的辛苦和汗水.“汗滴禾下土”,题题皆辛苦.
例1 (2016年土库曼斯坦数学奥林匹克)




注1:换元的目的之一是去根号.本题中,巧妙使用特定的三角换元一举消除两个根号.
例2 (2016年土库曼斯坦数学奥林匹克)
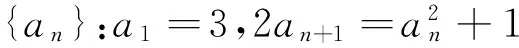
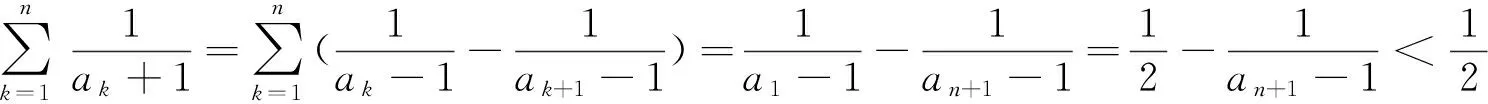

2016年土库曼斯坦数学奥林匹克中还有以下不等式题(留给读者练习):

例3 (2016年丝绸之路国际数学竞赛)
已知a,b,c是满足|(a-b)(b-c)(c-a)|=1的实数,求|a|+|b|+|c|的最小值.
解:不妨设a≥b≥c,则由均值不等式可得
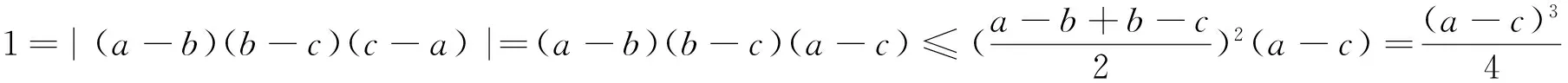
注3:增设条件(排序)的目的为的是去绝对值符号.


但不如前面的方法自然贴切,就如同下面的改编题远不如原题精彩一样:
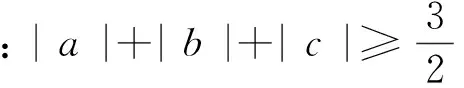
例4 (2016年澳大利亚数学奥林匹克)
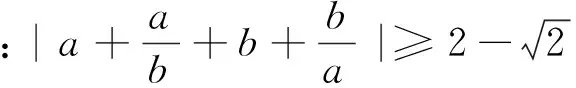


例5 (2016年阿塞拜疆数学奥林匹克)

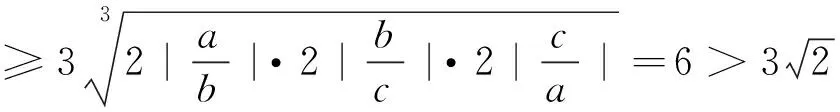
注5:均值不等式的特征之一是:“和”不小于“积”.剩下考虑的当然就是让字母“火并”.
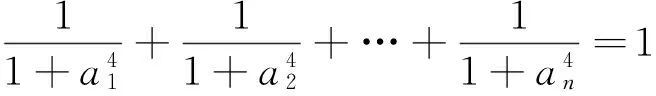
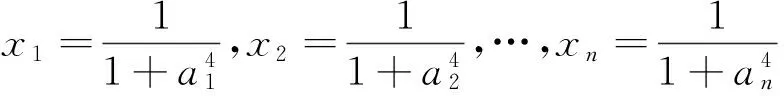
=(n-1)n,因此,原不等式成立.
注6:n=3时,本题即为2002年拉脱维亚数学奥林匹克试题.
将本题推广,宋庆老师获得并证明了下述结果:

例7 (2016年日本数学奥林匹克)已知a,b,c,d是满足ab+bc+cd=1的实数,求(a2+ac+c2)(b2+bd+d2)的最小值.
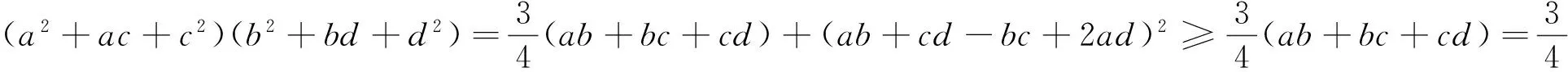
猜你喜欢
今日农业(2021年6期)2021-11-27 08:05:59
心声歌刊(2021年4期)2021-10-13 08:31:38
心声歌刊(2021年4期)2021-10-13 08:31:30
中学生数理化·七年级数学人教版(2020年3期)2020-08-10 08:59:31
中亚信息(2019年7期)2019-01-29 12:59:37
中学生数理化·八年级数学人教版(2016年1期)2016-03-16 01:47:46
大众考古(2014年9期)2014-06-21 07:11:12
中学生数理化·七年级数学人教版(2014年1期)2014-06-20 20:14:16
知识力量·教育理论与教学研究(2013年11期)2013-11-11 01:59:50
中国石油企业(2013年9期)2013-11-01 02:48:28

