一道2016年高考题的别解及推广

江苏省苏州第十中学 (215006)

项燕英



一道2016年高考题的别解及推广

江苏省苏州第十中学 (215006)

项燕英

2016年高考(四川卷)理科20题为

(1)求椭圆E的方程及点T的坐标；

(2)设O是坐标原点，直线l′平行于OT与椭圆E交于不同的两点A、B，且与直线l交于点P. 证明：存在常数λ，使得|PT|2=λ|PA|·|PB|，并求λ的值.

为方便，下面均假设相关直线斜率存在，若有斜率不存在的，只要在λ中令k→∞，所有结论全都成立.

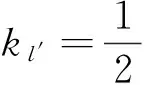
别证二要基于伸缩变换几个简单的性质：

根据上述方法，将情况一般化，不难得到

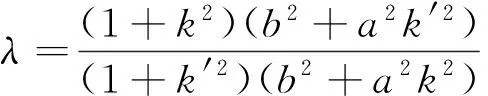
结论的证明与证法一、二完全相同，从略.更一般的，有

很显然，当k+k′=0时，λ=1，于是有

结论1，2中，若令a=b，则λ=1，此时椭圆变为圆，结论即为圆的切割线定理和相交弦定理.

在结论1,2,3中，以-b2代b2，则可得到双曲线中对应的结论：

证明从略. 在抛物线中有：

结论9 已知抛物线E:y2=2px(p>0)，过不在抛物线上的点P作斜率互为相反数的两直线分别与抛物线交于A、B和C、D，则|PC|·|PD|=|PA|·|PB|.

下面仅给出结论8的证明：

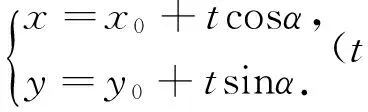
对结论3、6、9可以归纳为下面定理

定理 点P为不在圆锥曲线的一点，过点P作斜率互为相反数的两直线分别与圆锥曲线交于A、B和C、D，则|PC|·|PD|=|PA|·|PB|.

上述定理非常有用，2016年四川文20题就是本定理的应用，读者不妨一试.下面再举一例说明．

(1)求椭圆的标准方程；

(2)过点A，C，D的动圆记为圆Q，动圆Q过不同于A的定点，请求出该定点坐标．

本题(2) 常出现在各地各种考题中，常规方法难度大，运算量大，而用上述定理则极其简单．