弹载电动舵机幂次滑模反演控制

吕帅帅， 林辉， 陈晓雷， 李兵强

(西北工业大学 自动化学院， 陕西，西安 710129)



弹载电动舵机幂次滑模反演控制

吕帅帅， 林辉， 陈晓雷， 李兵强

(西北工业大学 自动化学院， 陕西，西安 710129)

针对高频响弹载电动舵机系统存在的齿隙非线性、参数时变、未知扰动等问题，提出一种幂次型快速Terminal滑模反演控制策略. 设计连续可微函数逼近齿隙非线性环节的死区模型，建立拟合系统的状态空间模型并划分为3个子系统进行控制设计. 采用反演控制思想设计快速幂次Terminal滑模控制器，内环采用直接转矩控制控制策略，提高响应速度. 应用Lyapunov方法证明闭环系统跟踪误差的有限时间收敛特性，实现了对齿隙非线性的精确补偿. 实验结果验证了所提出控制策略的有效性，与反演控制和PID控制策略相比，弹载电动舵机的控制精度、收敛速度及鲁棒性有显著提高.

高频响弹载舵机；永磁同步电机；快速幂次终端滑模控制；反演控制；齿隙非线性

制导炮弹作为现代炮兵的新型武器，近年来得到飞速的发展，如俄罗斯的M2制导炮弹、美国和瑞典联合研制的XM982神剑制导炮弹等[1]. 制导炮弹要求其控制系统具有高精度、高灵敏度及高可靠性，舵机作为飞控系统的执行机构，其静、动态特性直接影响到飞行器的操控性能. 制导炮弹弹载舵机具有体积小、频响高等特点，传统液压和气动舵机难以满足制导炮弹的性能要求[1]. 随着高性能机电伺服系统的发展，电动舵机的研究应用越来越广泛[2].

高性能伺服电机和先进控制技术是实现高性能舵机的关键因素，然而，永磁同步电机本身具有非线性、强耦合等特点. 此外，翼面存在气动弹性颤振，承受的铰链力矩与飞行姿态息息相关，其变化将对舵机的动态特性产生影响. 最关键的难题是，机构中存在减速机，必然产生啮合齿隙，造成动力延迟、噪声与振动，影响伺服系统动态性能与控制精度，成为制约电动舵机应用的关键因素[3].

齿隙具有动态及不可微特性，且难于精确测量，控制补偿极其困难. 现有补偿策略多集中于齿隙位于控制输入端的系统，通常采用建立齿隙逆模型或近似可微逆模型的方法[4-5]，抵消其影响. 然而对于电动舵机系统，齿隙环节无法简单折算到控制输入端，逆模型补偿策略无法适用，而采用齿隙的死区模型描述力矩传递关系更符合实际[6]，由此得到含齿隙的非线性系统. 由于该系统结构复杂，对其控制难度较大，研究成果并不多见. Shi等[4]采用可微函数拟合死区模型，并设计反推控制器，不足之处在于要求系统模型精确已知，而实际上死区模型的部分参数难以精确获得. Taware等[7]采用切换控制方法，在接触阶段及齿隙阶段设计不同的控制策略补偿齿隙效应，减小齿隙造成的机械冲击，其缺陷在于控制器结构过于复杂，工程实现难度较大.

反演控制的优势在于处理非匹配不确定的能力，灵活设计虚拟控制量可确保每个子系统的运动品质，是处理高阶非线性系统强有力工具[8]. 借鉴Huang等[9]的思想，设计连续可微函数逼近电动舵机系统中的齿隙非线性死区模型，将拟合误差表达为类似干扰项，建立含齿隙环节的电动舵机系统状态空间模型. 基于反推控制的设计思想，将整体模型划分为3个子系统进行控制器设计，利用幂次Terminal滑模算法设计虚拟控制量，实现系统跟踪误差的有限时间收敛.

为抑制弹载高频响电动舵机系统中齿隙非线性以及未知干扰的影响，提高动态性能，提出了一种快速幂次终端滑模反演控制. PMSM内环采用直接转矩控制策略，避免了矢量中电机参数时变对控制解耦的影响. 文中设计的控制律应用Lyapunov方法证明闭环系统跟踪误差的有限时间收敛特性，可实现对齿隙非线性的精确补偿及未知干扰的抑制，提高电动舵机的动态和稳态性能.

1 电动舵机系统模型

考虑齿隙作用，将制导炮弹的电动舵机系统分解为驱动部分和从动部分. 驱动部分由伺服电机、驱动器、控制器、传感器组成，从动部分包括减速机构和执行机构. PMSM的数学模型为[10]

(1)

式中：θ为转子机械角位移；ω为转子机械角速度；np为磁极对数；φf为转子永磁体在定子上的耦合磁链；J为折算到电机轴上的等效转动惯量；id、iq为定子电流矢量的d、q轴分量；bm为黏性摩擦系数，Tl为折算到电机轴上的负载力矩；R为绕组电阻；Ld、Lq为直轴和交轴电感；uq、ud为定子电压矢量的d、q轴分量.

对于减速机和执行机构的动力学，舵机力矩平衡方程为

(2)

式中：Jl为舵机机构转动惯量；θl为舵机转角；bl为舵机轴系统的黏性摩擦系数；η为传动机构减速比；Tf由摩擦力矩、惯性力矩及铰链力矩叠加折算而成，其中，铰链力矩构成最为复杂，与空气特性、马赫数、飞行高度、攻角等均有关系，当舵机处于收拢状态时，也会受到一定的气动铰链力矩T0. 简单起见，认为Tf与θl呈线性关系，为弹性负载

(3)

式中：kθ为负载力矩随舵面角度变化的转化系数，由于齿隙非线性的存在，负载力矩Tl与传动机构相对位移之间的关系可由如下死区模型表示[11]

(4)

式中：Δθ=θ-ηθl；2α为齿隙宽度；k为主从动齿轮啮合处的刚度系数. 由于齿隙造成系统存在不连续性，导致控制器设计困难，因此采用如下连续可微函数拟合死区函数[11]

(5)

式中γ为一常数.

定义拟合误差为

(6)

式中ε(Δθ)=(e-γΔθ-1)/(e-γΔθ+1).

由式(6)可得

(7)

(8)

将式(7)代入式(1)，PMSM的机械方程可写为

(9)

式中d2=-TΔ/J. 由式(8)(9)可知，将TΔ、T0相关项合并为非匹配不确定性d1、d2，称为类似误差项[12].

(10)

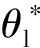
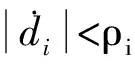
2 控制器设计

2.1 从动子系统设计

(11)

式中：α1、β1为正实数；l为大于1的正实数；q0、p0为奇数且满足p0>q0.

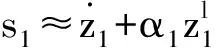
从行业角度看，作为PCB行业老大，深南电路显然是受益的。从公司的角度看，公司的亮点也颇多：1）技术领先提升盈利能力。深南电路拥有印制电路板、封装基板及电子装联三项业务，其中印刷电路板产品丰富，具有较强的竞争力，尤其是在高精密度和高多层PCB板产品方面具有显著优势，可实现最高100层、板厚径比20∶1等产品；封装基板打破国外垄断，成为全球先进半导体封测厂商合格供应商；电子装联可为PCB优质客户提供一站式服务。由于公司产品主要针对中高端市场，因此价格也高于行业平均水平，公司PCB均价为2800元/平米，而同行仅为800-1000元/平方米。

设计虚拟控制量θ*为

(12)

式中q、p为奇数且满足p>q.

对式(11)求导，并将式(8)代入可得

(13)

对于式(12)，θ即为虚拟控制量θ*，将其带入式(13)，可简化为

(14)

式中γ11+γ12=γ1.

(15)

2.2 PMSM机械子系统设计

对于PMSM的机械部分，控制任务是设计滑模控制器，使得θ在有限时间内跟踪上虚拟控制量θ*. 定义误差变量z2=θ-θ*，设计快速幂次终端滑模面为

(16)

(17)

2.3 PMSM电气子系统设计

为了提高PMSM的转矩的响应速度，满足制导炮弹舵机的高频响应特性，PMSM采用直接转矩控制方式，提高转矩控制的快速性. 直接转矩控制已有较多相关文献，此处不再赘述. 至此，已经完成控制律的设计.

2.4 收敛性分析

首先给出收敛性分析需要的引理.

引理1 若a1，a2，…，an及δ∈(0，2)皆为正实数，则如下不等式成立[13]

(18)

引理2 若连续可微Lyapunov函数V(t)满足如下不等式[13]

(19)

式中α，β>0，0<γ<1，则V(t)可在有限时间内收敛到零点，收敛时间为

(20)

定理1 对式(10)所示制导炮弹电动舵机伺服系统，虚拟控制律设计如式(12)(17)，若满足假设1～2，取适当的控制器参数，可使滑模面si(i=1，2)有限时间内可达，跟踪误差在有限时间内收敛到0.

证明 对式(16)求导，并将式(9)(17)代入，化简可得

(21)

(22)

(23)

由引理2可知，V可在有限时间t1内收敛到0，t1表达式为

(24)

则系统可在有限时间内到达滑模面. 结合终端滑模面性质，可知跟踪误差随后在有限时间收敛到0. 证毕.

3 实验分析研究

3.1 参数设置

为验证本文算法的有效性，在自行研制的高性能电动舵机伺服平台进行实验研究，实验结构主要包括驱动电源、控制器、驱动电机、减速机等. 控制器以DSP320F2812为核心进行设计，驱动电机采用表贴式永磁同步电机，减速机采用减速比为12的行星轮减速机. 电机的基本参数为：额定电压VDC=48 V，额定电流I=3.5 A，定子电阻Rs=0.5 Ω，定子电感Ls=0.85 mH，永磁体磁链ψf=0.075 Wb，ωN=5 000 r/min，极对数np=4，转动惯量J=0.6 g·m2.

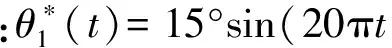
3.2 实验结果分析

将本文方法与两种控制方式进行对比研究：① 文献[12]的反演控制策略；② 经典PID控制方法. 控制器参数为：c1=4，c2=4，c3=15，c4=18；经反复实验调试，PID控制器参数设置如下：位置环参数：kPθ1=50，kIθ1=15，kdθ1=0.12，转速环：kPω1=24，kIω1=12，kdω1=0.08，实验结果分别如图1～图3所示.

图1是在PID控制方式下的实验结果，可以看出，PID控制方式下，位置跟踪相位滞后在1°左右，最大误差超过2.5°. 当指令信号的运动方向发生变化时，由于减速机和传统机构齿隙的作用，导致从动机构实际运动出现滞后跟踪，导致误差瞬间增大. 从PMSM的电磁转矩可以看出，齿隙作用对电磁转矩造成一定的干扰. 为了减小齿隙过渡时间，调整增大PI参数，位置误差如图1(d)所示，虽然在过间隙之前位置跟踪误差有所减小，但在渡过齿隙阶段后由于冲击作用导致跟踪误差呈现明显的振荡.

与图1对应，图2和图3分别是采用反演控制和本文方法的实验结果. 可以看出，反演控制的位置跟踪误差在1.2°，相位滞后0.5°左右，与PID相比，更有效地抑制了齿隙带来的影响；而在本文控制律的控制下，舵机位置跟踪的相位滞后减小到0.2°，误差抑制在0.5°以内，与反演控制和PID控制相比，齿隙影响的抑制效果最好，控制精度得到显著提升. 从PMSM电磁转矩波形可以看出，齿隙补偿控制的实质是在齿隙作用阶段激增一个瞬时控制量，使得系统快速渡过齿隙阶段，进而消除齿隙的影响. 从图3(c)的电磁转矩可以看出，补偿齿隙的控制量时间较短，如果激增的控制量时间过长，机构将会出现冲击，甚至出现震荡.

4 结 论

① 采用分块思想分块设计虚拟控制量，可降低常规反演或动态面控制需逐层递推的复杂程度，特别适用于高阶非线性系统，避免了精确线性化过程依赖建模精度的困难；

② 证明了滑模面有限时间可达及系统跟踪误差有限时间收敛性. 实验结果验证，该方法能够有效抑制减速机构齿隙带来的影响，与PID控制相比及反演控制相比，减小齿隙的影响，舵机控制精度显著提升；

③ 为提高舵机响应速度，降低电流环控制律设计的复杂程度，内环采用直接转矩方式.

理论分析和实验结果表明，本文提出的控制算法鲁棒性强，该方法可推广到其它驱动机构的伺服系统及多关节伺服系统的齿隙补偿设计中.

[1] 王生明.制导炮弹电动舵机控制器设计与分析[D].南京:南京理工大学，2010.

Wang Shengming. Design and analysis of guided projectile electromechanical actuator controller[D]. Nanjing: Nanjing University of Science and Technology， 2010. (in Chinese)

[2] 汪首坤，王军政.基于调频脉冲扫频的导弹舵机频率特性测试方法[J].北京理工大学学报，2006，26(8):697-699，703.

Wang Shoukun， Wang Junzheng. Aritificial frequency response testing method for missile actuator based on frequency modulated pulse sweep[J]. Transactions of Beijing Institute of Technology， 2006，26(8):697-699，703.(in Chinese)

[3] Kebairi A， Becherif M， El Bagdouri M. Modelling， simulation and identification of an engine air path electromechanical actuator [J]. Control Engineering Practice， 2015，34(1):88-97.

[4] Shi Zhiguang， Zong Yuzuo. Backstepping control for gear transmission servo systems with backlash nonlinearity[J]. IEEE Transactions on Automation Science and Engineering， 2015，12(2):752-757.

[5] 马艳玲，黄进，张丹.基于反步自适应控制的伺服系统齿隙补偿[J].控制理论与应用，2008，25(6):1090-1094.

Ma Yanling， Huang Jin， Zhang Dan. Backlash compensation in servo systems based on adaptive backstepping-control[J]. Control Theory & Applications， 2008，25(6):1090-1094. (in Chinese)

[6] Nordin M， Gutman P O. Controlling mechanical systems with backlash: a survey[J]. Automatica， 2002，38(10):1633-1649.

[7] Taware A， Tao G， Teolis C. Design and analysis of a hybrid control scheme for sandwich nonsmooth nonlinear systems[J]. IEEE Transactions on Automatic Control， 2002，47(1):145-150.

[8] Krstic M， Kanellakopoulos I， Kokotovic P V. Nonlinear and adaptive control design[M]. New York: John Wiley & Sons， 1995.

[9] Huang C， Jiao Z X， Shang Y X. Antiskid braking control with on/off valves for aircraft applications[J]. Journal of Aircraft， 2013，50(6):1869-1879.

[10] Ren Y， Zhu Z Q， Liu J M. Direct torque control of permanent-magnet synchronous machine drives with a simple duty ratio regulator[J].IEEE Transactions on Industrial Electronics， 2014，61(10):5249-5258.

[11] Merzouki R， Davila J A， Fridman L， et al. Backlash phenomenon observation and identification in electromechanical system[J]. Control Engineering Practice， 2007，15(4):447-457.

[12] Jing Zhou， Changyun Wen， Ying Zhang. Adaptive backstepping control of a class of uncertain nonlinear systems with unknown backlash-like hysteresis[J]. IEEE Transactions on Automatic Control， 2004，49(10):1751-1759.

[13] Shuanghe Yu， Xinghuo Yu， Shirinzadeh B， et al. Continuous finite-time control for robotic manipulators with terminal sliding mode[J]. Automatica， 2005，41(11):1957-1964.

(责任编辑：李兵)

Backstepping Power Fast Terminal Siding Mode Control for Missile Borne Electric Rudder

LÜ Shuai-shuai， LIN Hui， CHEN Xiao-lei， LI Bing-qiang

(College of Automation， Northwestern Polytechnical University， Xi’an， Shaanxi 710129， China)

In order to overcome the backlash nonlinearity， parameters variability and unknown disturbance for high response missile borne electric rudder servo， a backsteeping and power fast terminal siding mode (PFTSM) control algorithm was proposed. A continuously differentiable function zone model was designed to approximate backlash nonlinear. The state space model was formulated for the controller design as three subsystems. The power fast terminal siding mode controller was designed by using backstepping approaches. Direct torque control was applied to improve dynamic response for inner loop. Based on the Lyapunov stability analysis， it is shown that the proposed control strategy guarantees that asymptotic force tracking is achieved， all closed loop signals are ensured to be bounded. Experimental results show the effectiveness of the proposed method. Compared the PID and backtepping control， the precision， convergence speed and robustness are improved significantly for high response missile borne electric servo system.

high response missile borne electric servo; permanent magnet synchronous motors; power fast terminal siding mode control; backstepping control; backlash nonlinearity

2015-06-24

国家自然科学基金资助项目(51407143)；国家教育部高等学校博士学科点专项科研基金资助项目(20136102120049)；陕西省自然科学基础研究计划资助项目(2014JQ7264，2015JM5227)；中央高校基本科研业务费资助项目(3102014JCQ01066)；陕西省微特电机及驱动技术重点实验室开放基金资助项目(2013SSJ1002)

吕帅帅(1986—)，男，博士生，E-mail:lvshuai986@163.com；林辉(1957—)，男，教授，博士生导师，E-mail:linhui@nwpu.edu.cn.

V 19; TM 353

A

1001-0645(2016)10-1037-06

10.15918/j.tbit1001-0645.2016.10.010